2. 国家海洋信息中心,天津市六纬路93号,300171;
3. 国家自然资源部第一海洋研究所,青岛市仙霞岭路6号,266061
对GNSS ZTD估计的研究很多,但主要是建立在GPS观测数据的基础上。随着GLONASS系统的复苏和现代化计划,其空间星座分布和覆盖范围均获得显著改善。GPS/GLONASS组合系统可以增加可见卫星数,改善星座的空间几何分布,提高导航定位的可靠性和精确性,弥补单一系统在特殊情况下无法获得高精度结果的缺陷[1]。蔡昌盛等[2]采用精密单点定位GPS/GLONASS组合系统提取天顶对流层延迟,并与IGS提供的对流层产品进行比较得出,相比于GPS单系统,GPS/GLONASS组合系统估计的结果与IGS产品更相符,截止高度角和对流层参数波谱密度值的设置会对估计结果产生较大影响。王磊等[3]分别利用双差定位和精密单点定位提取GPS/GLONASS数据对流层延迟信息,证明GPS/GLONASS组合系统的结果精度优于GPS单系统。
沿海地区GNSS观测数据受多路径影响严重,质量较差,导致ZTD的提取精度低,而利用沿海GPS/GLONASS数据获得高精度ZTD的研究较少。本文结合沿海GNSS观测网数据,利用精密单点定位和双差定位方法分别估计GPS单系统、GLONASS单系统以及GPS/GLONASS组合系统ZTD,并分析各方法提取ZTD的精度,以确定沿海地区的数据处理方法。
1 GPS/GLONASS组合定位模型及处理策略GPS/GLONASS组合载波相位精密单点定位的观测方程见文献[4],GPS/GLONASS组合载波相位双差观测方程见文献[5]。从文献[5]可知,载波相位双差观测消除了卫星钟差,GLONASS精密卫星钟差数据对定位精度没有影响; 同时,其减弱了卫星星历误差、对流层和电离层延迟误差的影响。GPS卫星的双差观测还消除了接收机钟差的影响,由于GLONASS系统不同星座采用不同的频率,接收机钟差无法通过双差观测消除。
采用IGS欧洲定轨中心(CODE)提供的精密星历以及地球定向参数等产品。CODE提供的星历是GPS和GLONASS观测值同时处理获得的完全一致的轨道产品[6]。为了确保双差网解定位获得绝对的对流层延迟信息,在数据处理时,引入可同时接收GPS和GLONASS卫星信号的BJFS、NTUS、WUHN、PIMO等4个IGS站作为网外辅助站。利用精密单点定位或双差网解提取对流层延迟信息时,采用无电离层线性组合模式消除电离层一阶项影响,ZTD的干分量采用Saastamoinen模型[7]进行改正,残余湿分量作为参数进行估计,之后使用全球投影函数(GMF)将对流层延迟投影到传播路径上,同时考虑天线相位中心改正、天线相位缠绕效应改正、固体潮改正、大气负荷改正、海洋负载潮改正、极潮改正等。GPS数据模糊度采用准电离层(QIF)方法固定,GLONASS数据模糊度仅进行估计。其他详细的数据处理策略参见文献[8]。
2 数据处理与分析 2.1 数据及方案利用中国沿海GNSS观测网2014年年积日1~31期间20个连续运行基准站的双频GNSS观测数据(GNSS观测站分布见图 1),时间采样率为30 s。各基准站统一配备TOPCON NET-G3A接收机和TPSCR.G3扼流圈天线,可同时接收GPS和GLONASS卫星信号。采用4种方案对GPS/GLONASS数据进行处理,并评估不同方案下天顶对流层延迟的精度和可靠性:1)采用双差网解(DD),GPS/GLONASS组合数据; 2)采用精密单点定位(PPP),GPS/GLONASS组合数据; 3)采用双差网解(DD),GPS单系统数据; 4)采用双差网解(DD),GLONASS单系统数据。

|
图 1 GNSS观测站分布 Fig. 1 Distribution of the GNSS stations |
沿海地区GNSS观测数据受多路径效应影响严重,而在有的地区,改变截止高度角可以降低多路径效应。为此,分别设置10°和30°截止高度角,分别比较各方案提取天顶对流层延迟的精度。GPS/GLONASS数据处理除整周模糊度策略和定位方法不同外,其他策略相同,保证对流层延迟结果基本不受其他因素的影响。
2.2 低截止高度角结果及分析采用上述4种方案在10°截止高度角下处理沿海GNSS观测网的实测数据,得到各观测站1 h间隔的ZTD,并对各方案提取的结果进行对比分析。以双差网解GPS/GLONASS组合系统(方案1)提取结果为标准值,将其他方案解算的ZTD与其作比较,计算平均偏差(bias)和均方根误差(RMSE)。由于GNSS数据在个别时段存在缺失或观测质量差,导致解算结果不可靠,选择ZTD标准差大于15 mm作为异常值的检测指标[9],各方案结果的剔除比例均小于1%。从表 1中可以看出,4种方案提取的ZTD不存在明显的系统性偏差,RMSE都在mm级; 双差网解GPS单系统提取的ZTD与双差网解GPS/GLONASS组合系统结果差异最小,其次是精密单点定位GPS单系统提取结果,最后是双差网解GLONASS单系统。
|
|
表 1 天顶对流层延迟间差值的bias和RMSE统计结果 Tab. 1 RMSE and bias of differences between ZTDs |
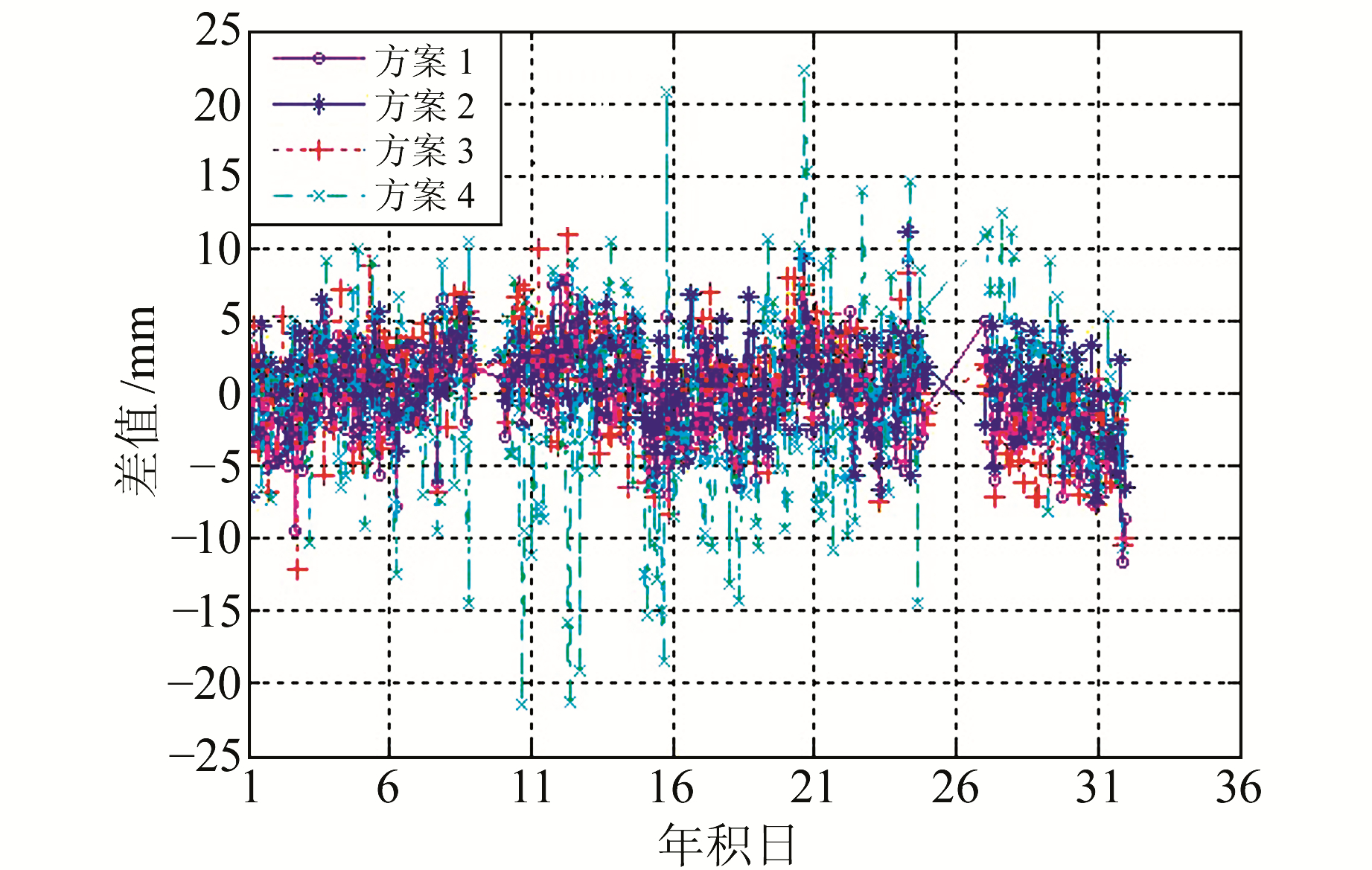
以CODE发布的IGS站ZTD为标准值,将各方案提取的ZTD与其进行比较。图 2为4种方案提取的BJFS站ZTD与CODE产品差值的时间序列。可以看出,方案1、2、3提取的结果与CODE产品偏差基本都在10 mm以内,最大偏差不超过15 mm; 方案4提取的ZTD与其他3种方案结果相比偏差较大,与CODE对流层产品的差值基本在20 mm以内。
|
图 2 4种方案提取的BJFS站ZTD与CODE结果的差值 Fig. 2 Differences between ZTD results estimated by the four schemes and CODE products at BJFS station |
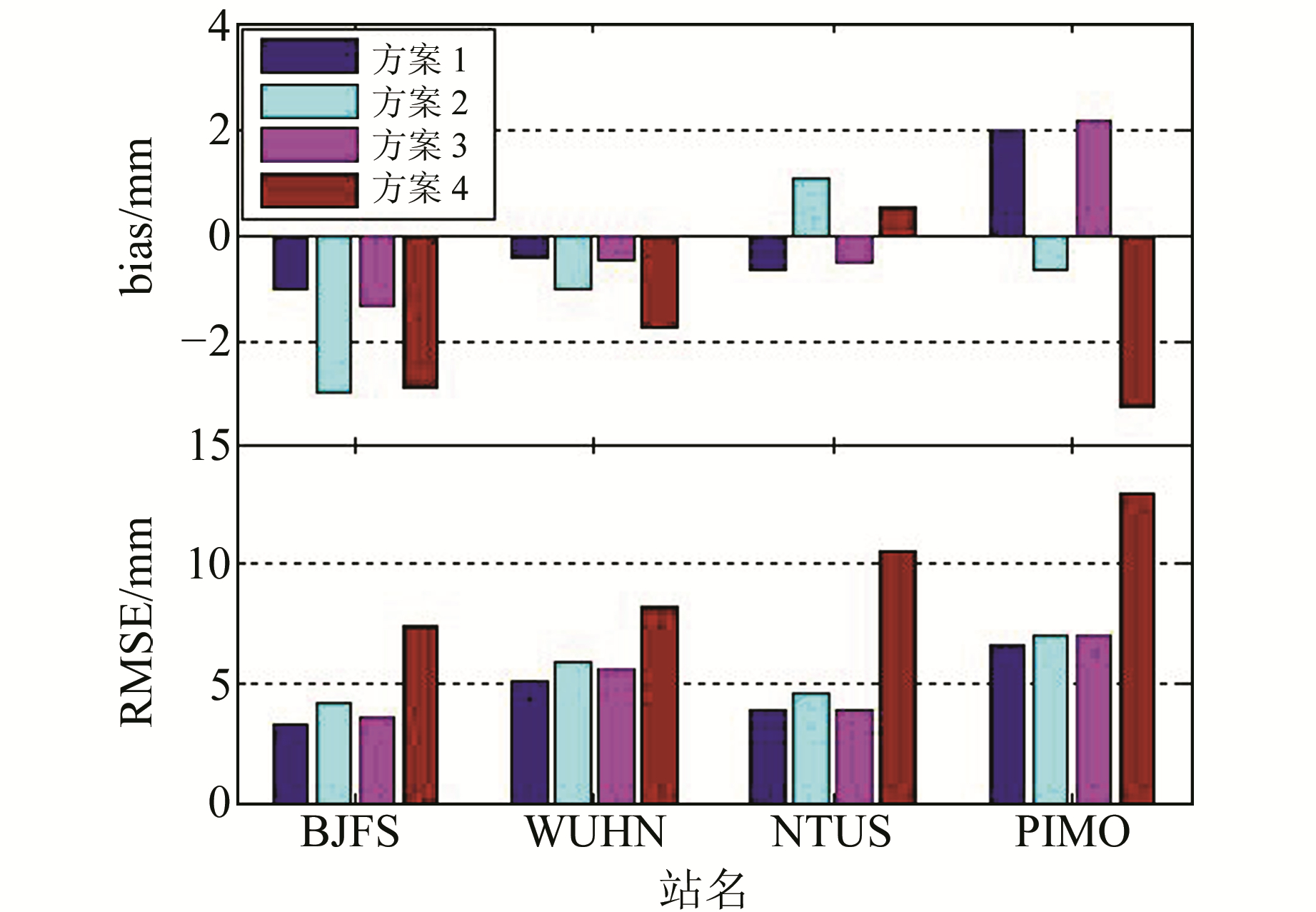
图 3给出了BJFS、NTUS、WUHN、PIMO等4个IGS站4种方案提取的ZTD与CODE对流层产品的bias和RMSE统计结果。可以看出,方案1、2、3提取的ZTD与CODE产品没有明显的系统差异,均方根误差都在6 mm以内; 方案4提取的ZTD与CODE产品差异明显变大,RMSE在10 mm左右。从4个IGS站的平均结果得出,双差网解GPS/GLONASS组合系统提取的ZTD精度最优,双差网解GPS单系统和精密单点定位GPS/GLONASS组合系统次之,双差网解GLONASS单系统最差。
|
图 3 10°截止高度角下IGS站ZTD与CODE产品差值的统计结果 Fig. 3 Statistical results of differences between ZTD and CODE products at IGS stations under 10° cut-off elevation angles |
为了评定各方案提取的沿海GNSS观测站的ZTD精度,结合地面实测气象数据将ZTD转换到可降水汽含量(PWV),并与同时刻的无线电探空结果进行对比。由ZTD到PWV的计算过程如下:1)由测站地面气压资料通过Saastamoinen模型计算对流层天顶静力学延迟ZHD; 2)从ZTD扣除ZHD,得到天顶湿延迟ZWD; 3)根据PWV=Π×ZWD计算PWV,其中Π是与加权平均温度Tm有关的无量纲系数,Tm采用按不同气候区建立的Tm-Ts模型系数[10]。沿海GNSS观测网中,与无线电探空站并址的GNSS观测站有BLHT、BXMD、DCHM、DXMN、NSTO、NHKO、NSYA。GNSS PWV与无线电探空结果比较之前,需要将探空结果改正到与GNSS观测站同一高度[11]。表 2给出了沿海7个测站各方案反演的GNSS PWV与探空结果的bias和RMSE。可以看出,各方案提取的PWV与探空结果的bias基本在1.5 mm以内,对应的RMSE基本在3 mm以内。对不同方案反演的可降水汽含量精度进行分析,双差网解GPS/GLONASS组合系统反演的PWV精度最优,平均RMSE为2.21 mm; 双差网解GPS单系统和精密单点定位GPS/GLONASS组合系统结果次之; 双差网解GLONASS单系统反演结果精度最差,平均RMSE达到3.10 mm。
|
|
表 2 不同方案反演的GNSS PWV与探空结果的bias和RMSE统计 Tab. 2 RMSE and bias between GNSS PWV retrieved by different schemes and radiosonde results |
选择截止高度角30°,同样利用上述4种方案对沿海20个测站GNSS数据进行处理,提取各站1 h间隔的ZTD。图 4给出了30°截止高度角下各方案提取的BLHT站ZTD结果。可以看出,方案1、2、3提取的ZTD变化趋势基本一致; 方案4提取的ZTD波动很大,与其他3种方案结果的最大偏差达到1.0 m以上。由此得出,当截止高度角较高时,GLONASS卫星观测数量较少,GLONASS系统已不具备独立定位的能力。因此,只比较方案2和3提取的ZTD与方案1结果的bias和RMSE,结果见表 3。在统计结果之前,剔除ZTD标准差大于15 mm的异常值,各方案结果的异常值所占比例均小于3%。从表中可见,各方案提取的ZTD间存在明显的系统性差异,并且不同测站的系统偏差和均方根误差差别较大。与10°截止高度角情况下各方案提取的ZTD间的差异相比,30°截止高度角各方案提取结果间的差异更加明显,且各方案结果间的差异在不同测站也更大。

|
图 4 不同方案提取的BLHT站天顶对流层延迟对比 Fig. 4 Comparison of ZTD estimated from different schemes at BLHT station |
|
|
表 3 不同方案提取的ZTD偏差统计结果 Tab. 3 Statistical results of differences between ZTDs extraced by different schemes |
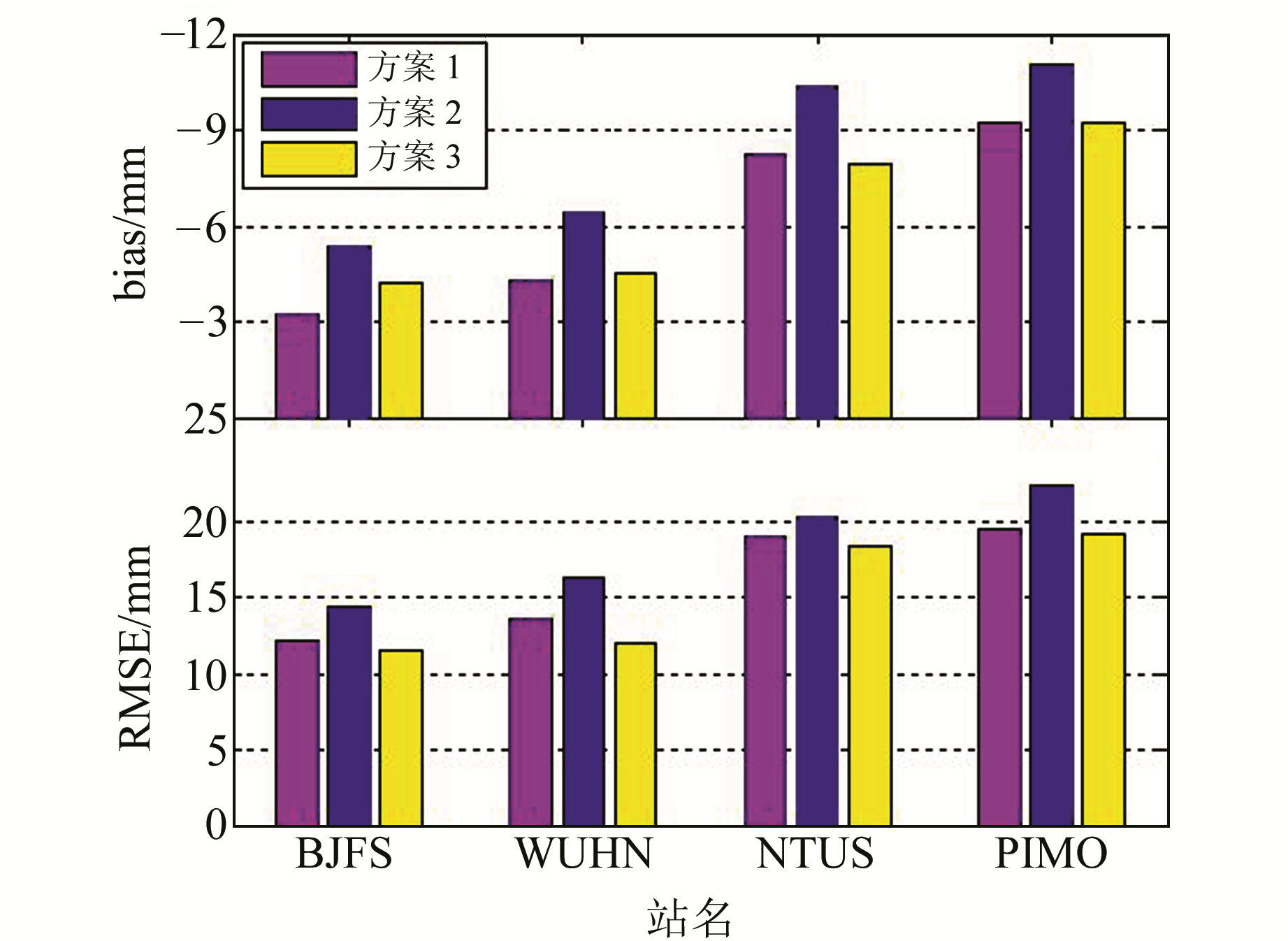
同样对30°截止高度角下不同方案提取的IGS站ZTD与CODE对流层产品进行比较。由图 5可知,3种方案提取的IGS站ZTD与CODE产品均存在明显的系统偏差,并且各站bias差异较大,该现象与蔡昌盛等[2]研究结果一致,无论是精密单点定位还是双差网解,截止高度角的改变都会显著影响天顶对流层延迟的精度; 各方案提取的ZTD与CODE结果的RMSE均在10 mm以上,相比于10°截止高度角精度明显变差。从各方案解算结果的精度分析,精密单点定位GPS/GLONASS组合系统提取的ZTD精度最差,双差网解GPS单系统提取结果精度略优于双差网解GPS/GLONASS组合系统。GLONASS卫星观测个数较少时,未知参数无法准确估计,该误差会带到GPS/GLONASS组合定位中,致使GPS/GLONASS组合定位精度变差。
|
图 5 30°截止高度角下IGS站ZTD与CODE产品差值的统计结果 Fig. 5 Statistical results of the differences between ZTD and CODE products at IGS stations under 30° cut-off elevation angles |
进一步统计沿海7个测站不同方案反演的GNSS PWV与探空结果的bias和RMSE,见表 4。可以看出,30°截止高度角情况下,各方案反演的PWV精度明显变差,并且同一方案下各站系统性差异差别较大,bias在0.60~3.96 mm之间,对应的RMSE为2.32~6.37 mm; 双差网解GPS单系统反演的PWV精度最高,其次为双差网解GPS/GLONASS组合系统,精密单点定位GPS/GLONASS组合系统反演结果精度最差。此外,各方案反演的PWV均明显低于探空结果,精密单点定位GPS/GLONASS组合系统反演的可降水汽含量结果最低。综合以上分析得出,较高的截止高度角并不能提高天顶对流层延迟信息的精度,如何获取多路径效应影响严重地区高精度的对流层延迟信息还有待进一步研究。
|
|
表 4 GNSS PWV与探空结果的bias和RMSE统计 Tab. 4 Statistics of bias and RMSE between GNSS PWV and radiosonde PWV |
1) 10°截止高度角情况下,采用双差网解GPS/GLONASS组合系统提取的天顶对流层延迟精度略优于双差GPS单系统和精密单点定位GPS/GLONASS组合系统,各方法提取结果不存在明显的系统偏差。
2) 30°截止高度角情况下,采用双差网解GPS单系统的估计结果精度要优于双差网解GPS/GLONASS组合系统和精密单点定位GPS/GLONASS组合系统,GLONASS系统不能实现单独定位。
3) 卫星截止高度角的改变会影响天顶对流层延迟精度,高截止高度角情况下,精密单点定位和双差网解定位提取结果精度明显变差,且存在低估现象。
| [1] |
Cai C S, Gao Y. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning[J]. GPS Solutions, 2013, 17(2): 223-236 DOI:10.1007/s10291-012-0273-9
(  0) 0) |
| [2] |
蔡昌盛, 夏朋飞, 史俊波, 等. 利用GPS/GLONASS组合精密单点定位方法估计天顶对流层延迟[J]. 大地测量与地球动力学, 2013, 33(2): 54-62 (Cai Changsheng, Xia Pengfei, Shi Junbo, et al. Estimation of Zenith Tropospheric Delay Using Combined GPS/GLONASS PPP Method[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 54-62)
(  0) 0) |
| [3] |
王磊, 万丽华, 解瑞楠, 等. 地基GNSS遥感可降雨量精度分析[J]. 导航定位学报, 2017, 5(4): 36-40 (Wang Lei, Wan Lihua, Xie Ruinan, et al. Accuracy Analysis of Remote Sensing on Precipitable Water Vapor by Ground-Based GNSS[J]. Journal of Navigation and Positioning, 2017, 5(4): 36-40)
(  0) 0) |
| [4] |
张小红, 郭斐, 李星星, 等. GPS/GLONASS组合精密单点定位研究[J]. 武汉大学学报:信息科学版, 2010, 35(1): 9-12 (Zhang Xiaohong, Guo Fei, Li Xingxing, et al. Study on Precise Point Positioning Based on Combined GPS and GLONASS[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 9-12)
(  0) 0) |
| [5] |
段举举, 沈云忠. GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报, 2012, 41(6): 825-830 (Duan Juju, Shen Yunzhong. An Algorithm of Combined GPS/GLONASS Static Relative Positioning[J]. Act Geodaetica et Cartographica Sinica, 2012, 41(6): 825-830)
(  0) 0) |
| [6] |
Dach R, Brockmann E, Schaer S, et al. GNSS Processng at CODE: Status Report[J]. Journal of Geodesy, 2009, 83(3): 353-365
(  0) 0) |
| [7] |
Saastamoinen J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[J]. Use of Artificial Satellite for Geodesy, 1972, 15(6): 247-251
(  0) 0) |
| [8] |
王朝阳, 周兴华, 张化疑, 等. 沿海GNSS观测网中BERNESE软件处理方案比较[J]. 海洋测绘, 2015, 35(1): 52-55 (Wang Zhaoyang, Zhou Xinghua, Zhang Huayi, et al. Comparison of BERNESE Software Processing Schemes: A Case Study in Coastal GNSS Observing Network[J]. Hydrographic Surveying and Charting, 2015, 35(1): 52-55 DOI:10.3969/j.issn.1671-3044.2015.01.014)
(  0) 0) |
| [9] |
Wang J H, Zhang L Y, Dai A G, et al. A Near-Global, 2-Hourly Data Set of Atmospheric Precipitable Water from Ground-Based GPS Measurements[J]. Journal of Geophysical Research, 2007, 112(D11)
(  0) 0) |
| [10] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 412-416 (Wang Xiaoying, Dai Ziqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416)
(  0) 0) |
| [11] |
Bock O, Bouin M N, Walpersdorf A, et al. Comparison of Ground-Based GPS Precipitable Water Vapour to Independent Observations and NWP Model Reanalyses over Africa[J]. Quarterly Journal of the Royal Meteorological Society, 2010, 133(629): 2 011-2 027
(  0) 0) |
2. National Marine Information Center, 93 Liuwei Road, Tianjin 300171, China;
3. The First Institute of Oceanography, MNR, 6 Xianxialing Road, Qingdao 266061, China
 2019, Vol. 39
2019, Vol. 39

