动态导航定位通常采用Kalman滤波方法。经典Kalman滤波是在状态噪声和观测噪声均为零均值白噪声的情形下提出的一种递推线性最小方差估计方法。然而在实际工程应用中,状态噪声和观测噪声往往存在有色噪声,这时采用经典Kalman进行数据滤波处理可能会导致滤波发散或结果失真[1]。针对有色噪声问题,许多学者提出了解决方法,包括函数模型补偿滤波和随机模型补偿滤波[2-6]。在滤波时,观测值和状态预报信息的相关特性都会在观测残差(或新息序列)和状态残差中得到充分体现,故可以使用观测残差序列和状态残差序列对Kalman滤波进行函数模型补偿。
本文根据有色噪声的特点,提出一种简便的有色噪声函数模型拟合滤波算法,通过建立合适的有色噪声函数模型,对动态滤波过程中的有色噪声进行补偿,从而减弱或控制有色噪声对滤波解的影响。
1 函数模型拟合滤波有色噪声处理算法以GPS系统时间为参考时间,四系统伪距观测方程可表示为[7]:
| $ \left. \begin{array}{l} {P^{\rm{G}}} = {\rho ^{\rm{G}}} + c{\rm{d}}t - c{\rm{d}}{T^{\rm{G}}} + d_{{\rm{orb}}}^{\rm{G}} + d_{{\rm{trop}}}^{\rm{G}} + d_{{\rm{ion}}}^{\rm{G}} + b_P^{\rm{G}} + \varepsilon _P^{\rm{G}}\\ {P^{\rm{R}}} = {\rho ^{\rm{R}}} + c{\rm{d}}t + c{\rm{d}}t_{{\rm{sys}}}^{{\rm{R}}, {\rm{G}}} - c{\rm{d}}{T^{\rm{R}}} + d_{{\rm{orb}}}^{\rm{R}} + d_{{\rm{trop}}}^{\rm{R}} + d_{{\rm{ion}}}^{\rm{R}} + b_P^{\rm{R}} + \varepsilon _P^{\rm{R}}\\ {P^{\rm{E}}} = {\rho ^{\rm{E}}} + c{\rm{d}}t + c{\rm{d}}t_{{\rm{sys}}}^{{\rm{E}}, {\rm{G}}} - c{\rm{d}}{T^{\rm{E}}} + d_{{\rm{orb}}}^{\rm{E}} + d_{{\rm{trop}}}^{\rm{E}} + d_{{\rm{ion}}}^{\rm{E}} + b_P^{\rm{E}} + \varepsilon _P^{\rm{E}}\\ {P^{\rm{C}}} = {\rho ^{\rm{C}}} + c{\rm{d}}t + c{\rm{d}}t_{{\rm{sys}}}^{{\rm{C}}, {\rm{G}}} - c{\rm{d}}{T^{\rm{C}}} + d_{{\rm{orb}}}^{\rm{C}} + d_{{\rm{trop}}}^{\rm{C}} + d_{{\rm{ion}}}^{\rm{C}} + b_P^{\rm{C}} + \varepsilon _P^{\rm{C}} \end{array} \right\} $ | (1) |
式中,上标G、R、E、C分别代表GPS、GLONASS、Galileo和BDS卫星系统,P为伪距观测值,ρ为卫星至接收机的几何距离,线性化后用于估计位置参数,c为光速,dt为接收机钟差,dT为卫星钟差,dorb为投影至视距方向的卫星轨道偏差,dtrop为对流层延迟,使用Hopfield模型进行改正,dion为电离层延迟,使用Klobuchar或者NeQuick模型进行改正,bP为码观测值硬件延迟偏差,接收机端硬件延迟将被接收机钟差和系统时间偏差参数吸收,卫星端的硬件延迟偏差通过广播星历中提供的群时延进行改正,cdtsysR, G、cdtsysE, G、cdtsysC, G分别为GPS-GLONASS、GPS-Galileo和GPS-BDS的系统时间偏差[7],εP为包括多路径偏差在内的码观测噪声。卫星轨道和卫星钟差由广播星历计算,待估参数包括接收机的三维坐标、接收机钟差和3个系统时间差参数。
将待估参数设为状态矩阵X,Kalman滤波线性化后的方程为:
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{L}}_k} = {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{e}}_k}}\\ {{{\bf{X}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k \cdot k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{W}}_k}} \end{array}} \right\} $ | (2) |
式中,Lk为观测向量,Ak为观测设计矩阵,Xk、Xk-1分别为k、k-1时刻的系统状态,Φk, k-1为状态转移矩阵,ek和Wk为统计特性已知的零均值高斯白噪声序列。当观测噪声ek和状态噪声Wk并不是统计特性已知的零均值高斯白噪声时,有色观测噪声和有色状态噪声的函数模型可表示为一阶自相关模型:
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_k} = {\mathit{\boldsymbol{B}}_{k,k - 1}}{\mathit{\boldsymbol{e}}_{k - 1}} + {\mathit{\boldsymbol{\eta }}_k}}\\ {{\mathit{\boldsymbol{W}}_k} = {\mathit{\boldsymbol{C}}_{k,k - 1}}{\mathit{\boldsymbol{W}}_{k - 1}} + {\mathit{\boldsymbol{\xi }}_k}} \end{array}} \right\} $ | (3) |
式中,e为有色观测噪声,W为有色状态噪声,B、C分别为有色观测噪声和有色状态噪声的模型系数矩阵,ηk、ξk为统计特性已知的零均值高斯白噪声序列。
函数模型拟合滤波是基于观测残差和状态预测残差建立相应的有色观测噪声和有色状态噪声的函数模型,计算出当前历元的有色观测噪声和有色状态噪声估值,并在动态Kalman滤波过程中使用经过有色噪声估值修正后的观测值和状态预报值进行解算[8]。本文采用简便的窗口均值算法对观测噪声和状态噪声进行拟合,设基于残差序列计算出的有色观测和状态噪声的预报值分别为:
| $ \left. \begin{array}{l} {{\mathit{\boldsymbol{\bar e}}}_k} = a \times \sum\limits_{j - m}^{j - 1} \mathit{\boldsymbol{V}} /m\\ {\mathit{\boldsymbol{\overline W}} _k} = b \times \sum\limits_{k - m}^{k - 1} {{\mathit{\boldsymbol{V}}_{\bar X}}} /m \end{array} \right\} $ | (4) |
式中,
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{L}}_k} + {{\mathit{\boldsymbol{\bar e}}}_k} = {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{\eta }}_k}\\ {\mathit{\boldsymbol{X}}_k} = \left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {{\mathit{\boldsymbol{\bar W}}}_k}} \right) + {\mathit{\boldsymbol{\xi }}_k} \end{array} \right\} $ | (5) |
上式符合Kalman滤波条件,可以直接获得滤波解。有色噪声预报值与进行预报的模型系数估值密切相关,因此计算模型系数估值至关重要。图 1为函数模型拟合滤波算法流程。
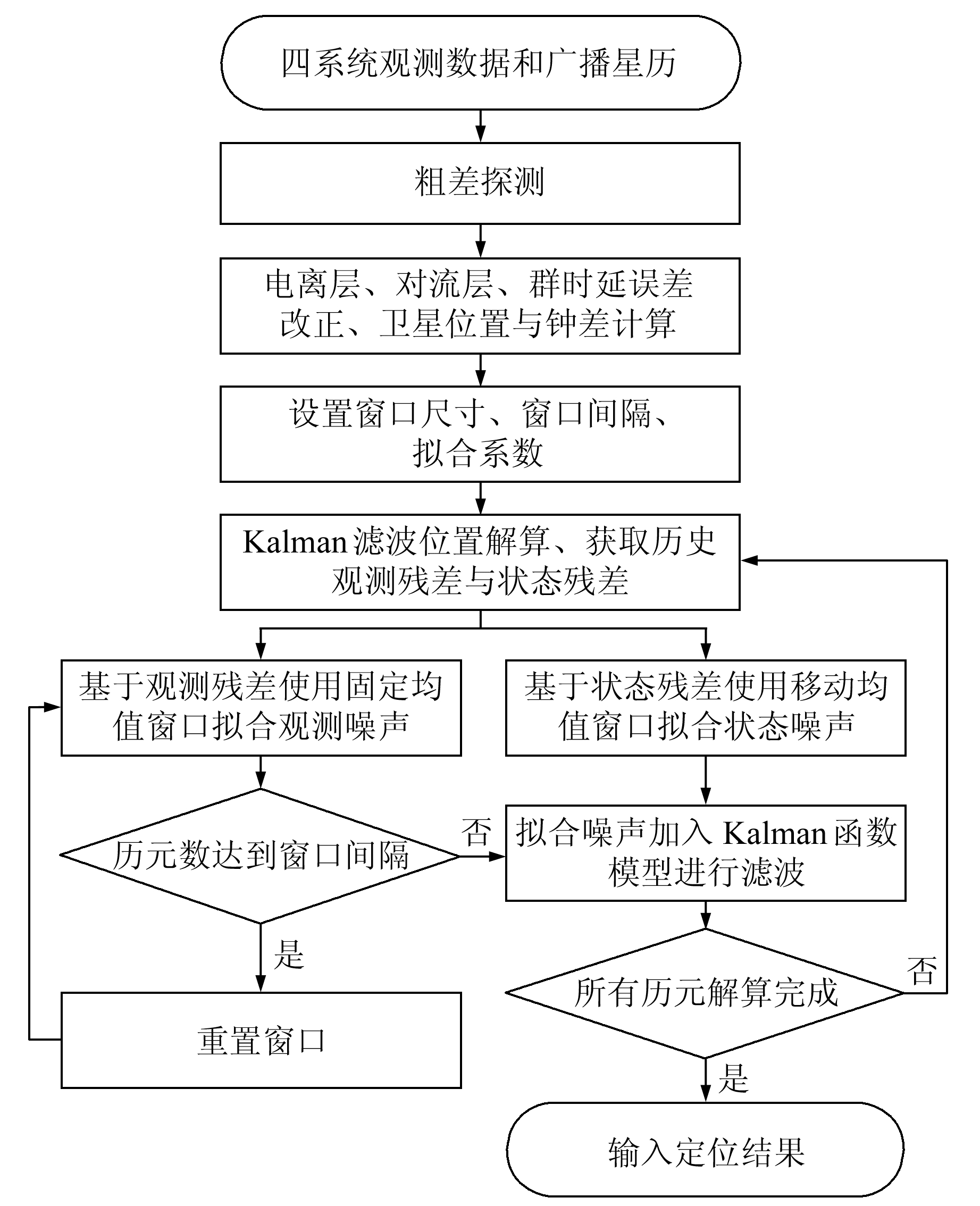
|
图 1 基于有色噪声函数模型拟合的Kalman滤波位置解算算法流程 Fig. 1 Process of Kalman filtering algorithm for position calculating based on the color noise function model fitting |
为了研究动态定位中观测残差与状态预报残差是否具有系统性偏差,使用IGS观测站四系统数据进行静态模拟动态定位实验,采样间隔30 s,截止高度角设置为10°,拟合窗口尺寸设为5,观测噪声拟合系数为0.8,状态噪声拟合系数为-1,重置窗口的间隔定为60历元,以IGS提供的测站坐标值为真值。
使用未顾及有色噪声的经典Kalman算法与顾及有色噪声的Kalman算法分别进行处理,表 1给出KIRU测站在使用顾及有色噪声滤波前后各方向误差的RMS值对比。为了更直观地表现定位精度,统计当天00:00~04:00的数据(图 2)。可以看出,在使用函数模型拟合滤波后,得到的结果更接近测站真值,各个方向的误差更小,说明顾及有色噪声的方法具有明显的优势。
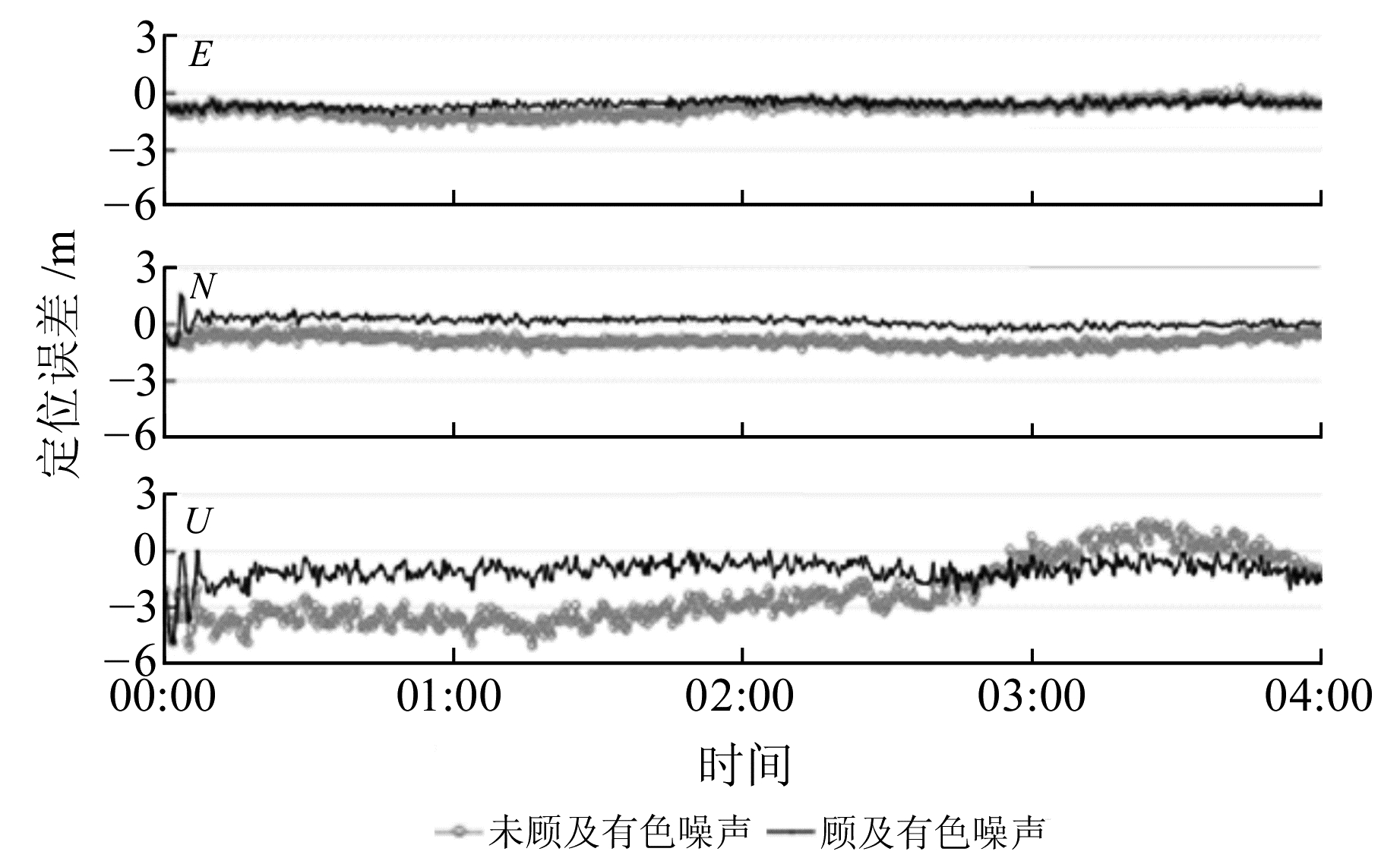
|
图 2 KIRU测站3个方向定位误差对比 Fig. 2 Comparison of positioning errors in three directions at KIRU station |
|
|
表 1 KIRU测站单点定位精度统计 Tab. 1 Accuracy statistical table of single point positioning accuracy at KIRU station |
选取全球多个MGEX测站进行2种方法的对比,所选测站均能够接收GPS/GLONASS/BDS/Galileo四系统卫星数据,处理结果见图 3,横轴为测站名称,纵轴为改善程度。可以看出,使用函数模型拟合滤波算法后,单点定位三维位置精度相比经典Kalman滤波算法最高改善33%,数个测站能够达到20%以上,绝大部分测站能够改善3%以上,平均改善程度为9.5%。通过试算,确定的窗口尺寸在3~10,观测噪声的拟合系数在0.1~1,状态噪声的拟合系数在-1~-0.1。
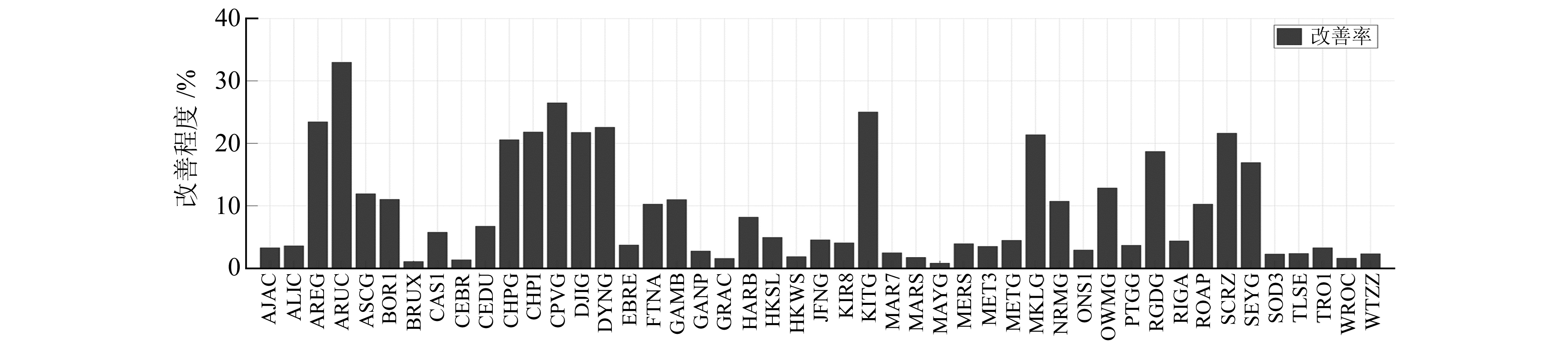
|
图 3 使用函数模型拟合滤波算法的MGEX测站单点定位精度改善程度 Fig. 3 Improvement of accuracy of single point positioning accuracy at MGEX station by using function model fitting filtering |
为了进一步验证该算法,采用野外动态实验数据进行计算。野外实验观测采样间隔为1 s,截止高度角设置为10°,噪声拟合窗口尺寸设为5,观测噪声拟合系数为1,状态噪声拟合系数为-0.3,重置窗口的历元间隔为60。采用2种方法分别进行解算,求得动态单点定位的位置坐标,使用事后精密单点定位位置解作为参考值。由于本次实验接收到的Galileo卫星数据较少而且质量较差,故未参与解算。
图 4为GPS、GLONASS、BDS系统各2颗卫星在顾及有色噪声前后观测噪声的情况。可以看到,在顾及有色噪声后,观测噪声整体上都得到一定的减弱(图中的突变是受到粗差的影响)。图 5中状态预测残差为每个历元先验估计与后验估计的偏差,其也得到一定程度的削弱,表现为在大多数历元波动有所减小。

|
图 4 动态定位中2颗不同GPS、GLONASS和BDS卫星的观测残差序列对比 Fig. 4 Comparison of observation residual sequences for two different GPS, GLONASS and BDS satellites kinematic positioning |
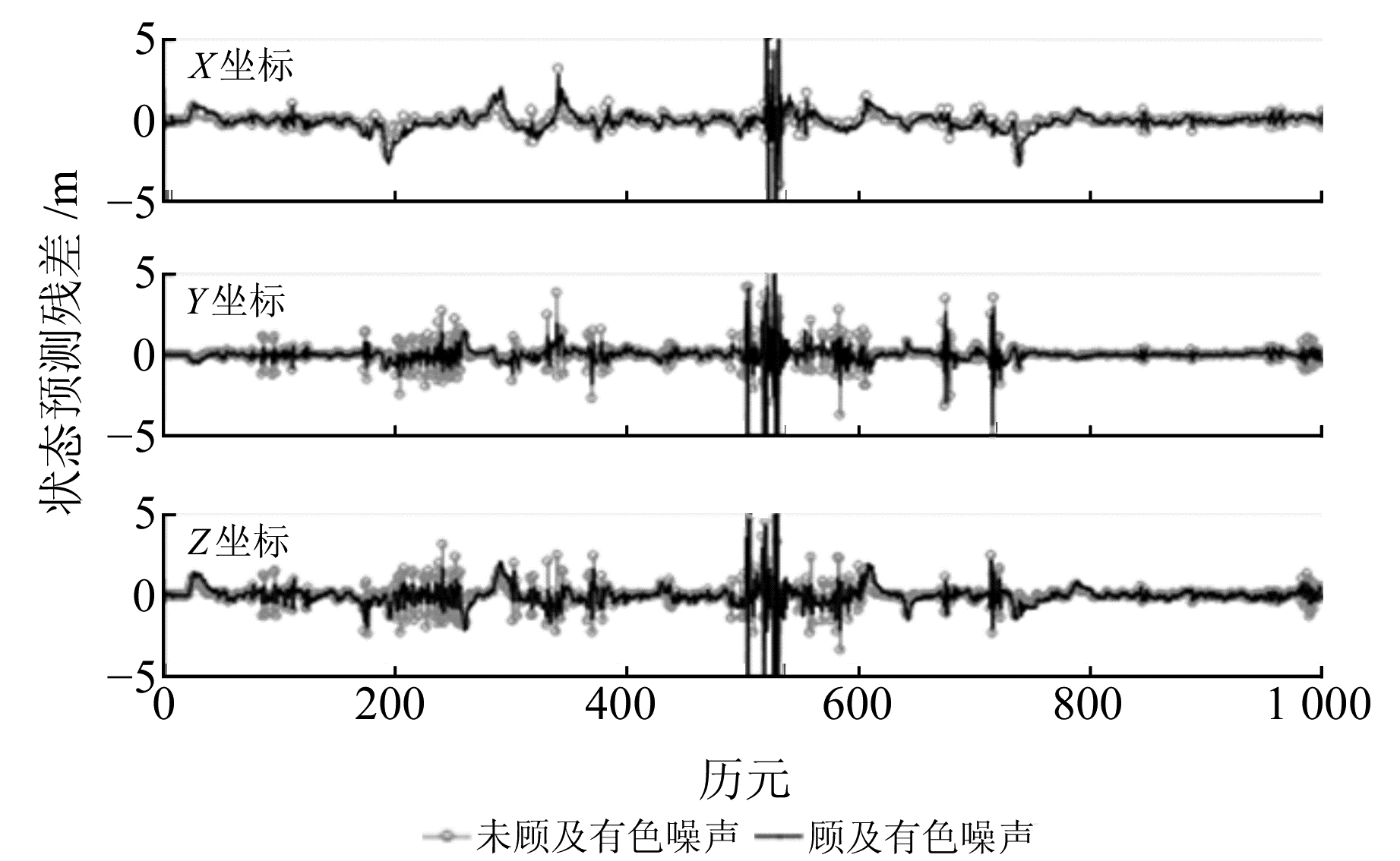
|
图 5 动态定位状态预测残差序列对比 |
表 2给出动态单点定位的RMS精度统计。可以看出,使用函数模型拟合滤波后,动态单点定位精度有所提升,三维位置精度提升12.5%。受粗差以及观测条件的影响,定位精度相对于静态模拟动态定位有所下降。
|
|
表 2 动态单点定位精度统计 Tab. 2 Accuracy statistical of dynamic single point positioning |
如果观测序列和状态预报序列中存在有色噪声,可以通过建立有色噪声模型进行预报来改善观测模型和动力学模型,从而减弱有色噪声对状态参数估值的影响。本文提出一种简便的有色噪声函数模型拟合滤波算法,采用窗口均值的方法进行噪声拟合,考虑到噪声的时间相关会随着时间的推移而降低,每间隔一定数量的历元对观测噪声再次用历史残差数据进行拟合,采用移动窗口拟合状态噪声。使用47个MGEX测站数据进行静态模拟动态实验,在使用顾及有色噪声的函数模型拟合滤波后,三维位置精度相比未顾及有色噪声平均提升9.5%。野外动态实验处理结果表明,三维位置精度的改善率达到12.5%。
| [1] |
赵长胜, 陶本藻. 有色噪声作用下的卡尔曼滤波[J]. 武汉大学学报:信息科学版, 2008, 33(2): 180-182 (Zhao Changsheng, Tao Benzao. Kalman Filtering of Linear System with Colored Noises[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 180-182)
(  0) 0) |
| [2] |
崔先强, 杨元喜, 高为广. 多种有色噪声自适应滤波算法的比较[J]. 武汉大学学报:信息科学版, 2006, 31(8): 731-735 (Cui Xianqiang, Yang Yuanxi, Gao Weiguang. Comparison of Adaptive Filter Arithmetics in Controlling Influence of Colored Noises[J]. Geomatics and Information Science of Wuhan University, 2006, 31(8): 731-735)
(  0) 0) |
| [3] |
Choi H D, Ahn C K, Lim M T. Time-Domain Filtering for Estimation of Linear Systems with Colored Noises Using Recent Finite Measurements[J]. Measurement, 2013, 46(1): 2792-2797
(  0) 0) |
| [4] |
杨元喜, 任夏, 许艳. 自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报, 2013, 1(1): 9-15 (Yang Yuanxi, Ren Xia, Xu Yan. Main Progress of Adaptively Robust Filter with Applications in Navigation[J]. Journal of Navigation and Positioning, 2013, 1(1): 9-15 DOI:10.3969/j.issn.2095-4999.2013.01.003)
(  0) 0) |
| [5] |
Sui L F, Mou Z K, Gan Y, et al. Unscented Kalman Filter Algorithm with Colored Noise and Its Application in Spacecraft Attitude Estimation[C]. The 1st International Workshop on the Quality of Geodetic Observation and Monitoring Systems, 2015
(  0) 0) |
| [6] |
邹韬, 赵长胜, 丁圳祥. 有色观测噪声下的无迹卡尔曼滤波算法[J]. 测绘通报, 2015(6): 24-27 (Zou Tao, Zhao Changsheng, Ding Zhenxiang. Unscented Kalman Filter of Nonlinear Systems with Colored Measurement Noise[J]. Bulletin of Surveying and Mapping, 2015(6): 24-27)
(  0) 0) |
| [7] |
Cai C S, Gao Y, Pan L, et al. Precise Point Positioning with Quad-Constellations: GPS, Beidou, GLONASS and Galileo[J]. Advances in Space Research, 2015, 56(1): 133-143 DOI:10.1016/j.asr.2015.04.001
(  0) 0) |
| [8] |
杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006 (Yang Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. Beijing: Surveying and Mapping Press, 2006)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

