2. 中国地震局地质研究所,北京市华严里甲1号,100029;
3. 中国地震局地震预测研究所,北京市复兴路63号,100036;
4. 云南省测绘工程院,昆明市虹山西路39号,650033
GPS时间序列空缺的插值对于时间序列分析和应用具有重要作用。当时间序列间断较短时,可以使用一般的插值方法[1],但间断时间较长时,一般的插值方法效果并不理想,甚至会严重影响分析结果。符养[2]针对坐标时间序列缺失,提出按间断天数的不同分类进行插值的思想。武艳强等[3]提出多点三次样条插值的方法,在一定条件下可以解决时间序列处理中较多数据缺失的问题。Dong等[4]按间断情况分3种方式来插值,其中长空缺采用模型和噪声重构的方法完成内插。邱荣海等[5]和Wang等[6]利用奇异谱分析方法、Xu[7]采用迭代的经验正交函数插补时间序列空缺,但两者必须对嵌套空间维数选择进行合理验证, 且不能很好地处理阶跃[6-7]。
本文改进了Dong等[4]提出的模型和噪声重构的插值方法,分析噪声相关性,利用相关性较高的站点来重构噪声,可以有效避免局部信号产生的污染。最后,以陕西省GPS连续站时间序列数据为例,检验该方法的可靠性。
1 基于模型和空间相关性的插值方法首先,对GPS坐标时间序列进行建模,提取出各站各方向的噪声时间序列;然后,分析噪声的空间相关性,利用相关系数高的噪声时间序列来重构空缺处的噪声;最后,将模型值与重构噪声值之和作为空缺处的插值,流程见图 1。
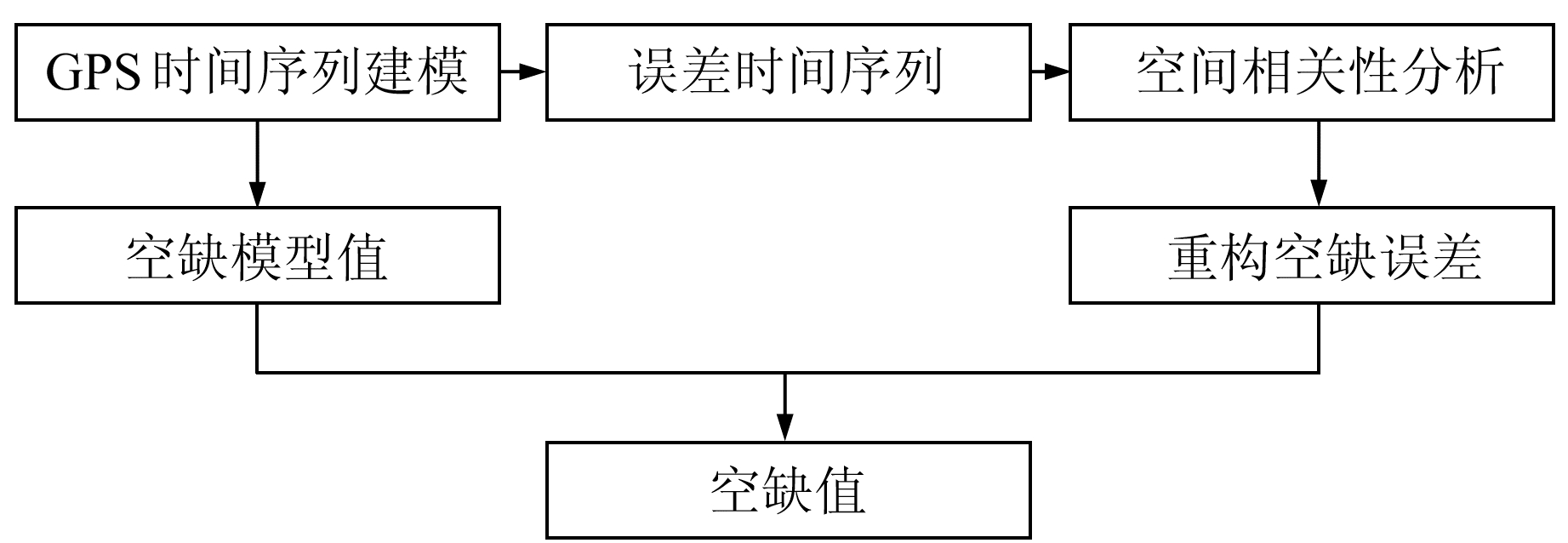
|
图 1 程序流程 Fig. 1 Program flow chart |
原始GPS时间序列包含了站点速度、天线移动或设备更换引起的阶跃、同震和震后形变、年周期和半年周期的季节项,还有一些未模型化的瞬态形变和噪声, 坐标时间序列模型见文献[8]。
利用皮尔森相关系数[9]来分析各GPS站噪声的空间相关性。针对存在空缺的站点,选取相关性较高的站点参与噪声重构。噪声重构过程[4]为:首先,将各站噪声时间序列的加权平均值作为空缺历元的初始噪声;然后,将各站的噪声时间序列组建噪声矩阵进行主成分分析[10],利用前几个主成分和特征向量即可重构噪声矩阵。将重构的噪声赋值到空缺处再次进行主成分分析,这里采用迭代的方式,直到空缺处噪声变化小于10-6。
2 实例分析采用GAMIT/GLOBK解算陕西省GPS连续站时间序列[11]。以SNFG站为例,建立模型[8]拟合GPS坐标时间序列(图 2,黑点为原始观测值,红线为拟合值)。可以看出,模型很好地拟合了GPS坐标时间序列,N、E、U方向残差RMS值分别为2.15 mm、1.82 mm、5.13 mm,观测值与模型值的差即为噪声时间序列。
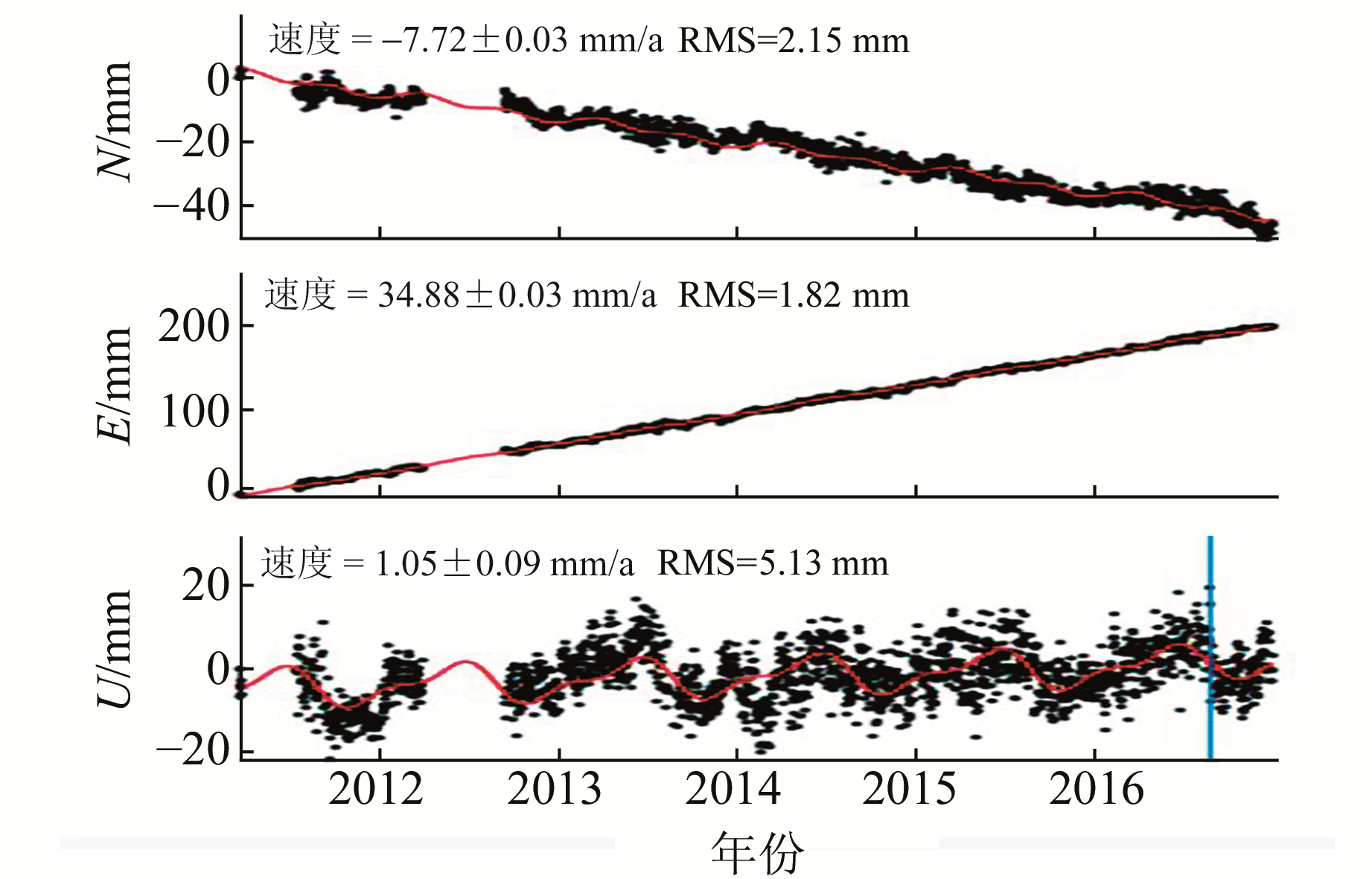
|
图 2 SNFG坐标时间序列和模型拟合 Fig. 2 SNFG coordinate time series and its model |
利用相同方法处理陕西省其他GPS站坐标时间序列,得到各站N、E、U方向的噪声时间序列(图 3)。可以看出,各GPS站的噪声时间序列具有相似性,即共模噪声。共模噪声具有一定的空间相关性[4],可能源自卫星轨道误差、水体和大气质量负荷、参考框架定义的不确定性等[4, 12-13]。
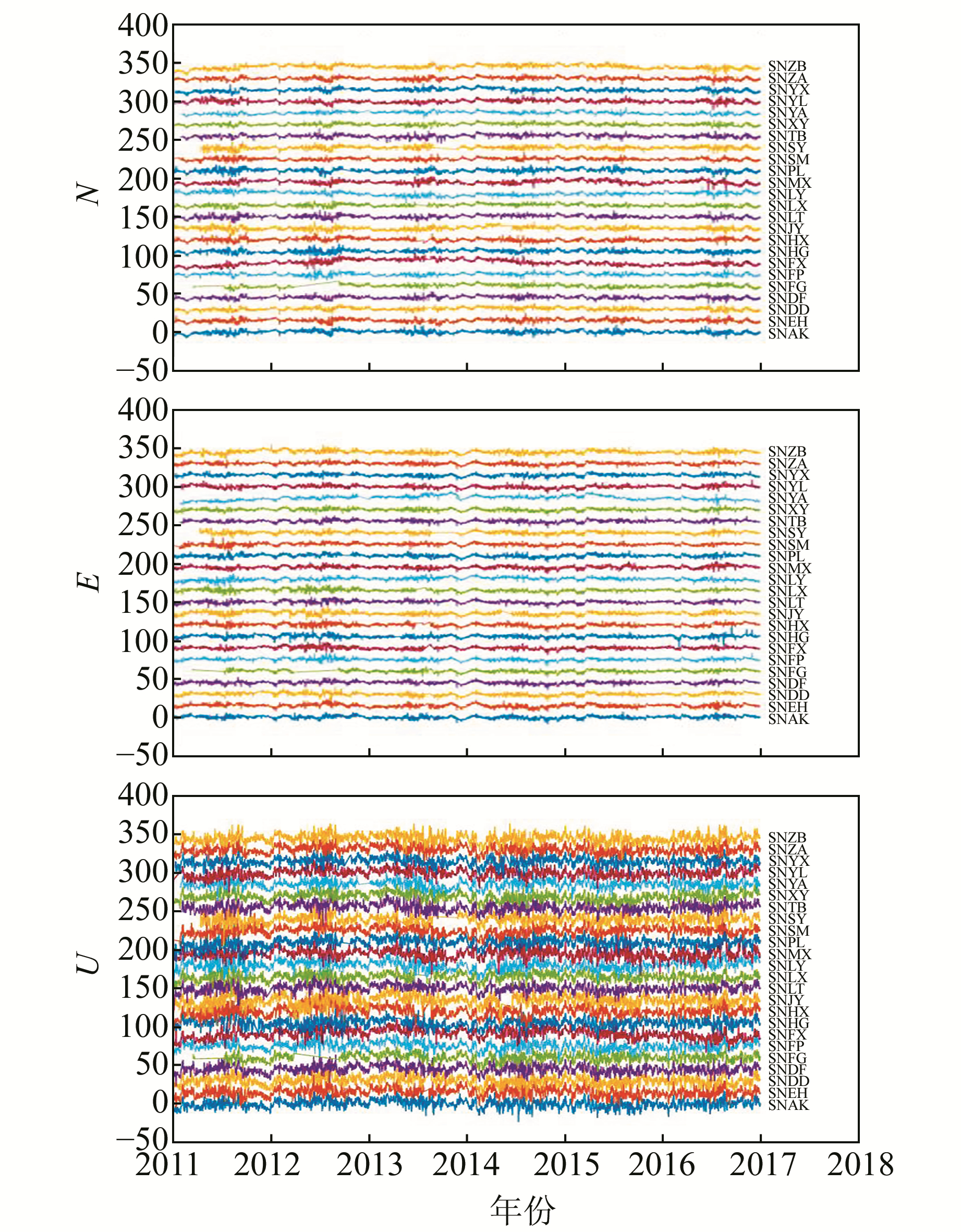
|
图 3 陕西省GPS连续站N、E、U方向噪声时间序列 Fig. 3 Noise time series in N, E, U direction of continuous GPS sites in Shaanxi |
图 4显示了SNFG站与其他GPS站噪声的相关系数(图 4(a)~(c))以及相关系数与距离的关系(图 4(d)~(f))。可以看出,噪声的空间相关性随距离的增加而减弱,这可能和与距离相关性较高的电离层、对流层残差、水体大气负载等有关。个别站相关性的偏离与站点自身的噪声特性或者未模型化的局部运动有关,如SNYA和SNLY站分别受延安新城改造和滑坡的影响,导致相关性较弱。整体来看,E方向相关性最强,N方向次之,U方向最弱,这与N、E、U方向的GPS时间序列拟合精度一致。设0.5为空间相关性阈值,将SNPL、SNMX、SNLV、SNYA站剔除误差重构过程,避免将局部运动引入到SNFG站噪声中。
SNFG站数据完整率为83.98%,其中2011~2012、2012~2013年存在2个长空缺,空缺天数分别为110 d和167 d,其余为离散空缺。图 5分别表示线性插值法、二阶拉格朗日多项式插值法及基于模型和空间相关性插值法的插值结果,黑点表示原始坐标时间序列,红点表示插值。可以看出,基于模型和空间相关性插值法对于长空缺插值具有明显的优势,线性插值法次之,拉格朗日多项式插值法在长空缺处扭曲明显。线性插值法对水平方向以线性趋势为主的插值表现不错,但不能还原垂向很强的周期性运动。这是由于线性插值是对两点之间的线性近似处理会随着时间序列二阶导数的增大而逐渐变差,曲率越大,线性插值噪声就越大。而拉格朗日插值法对于长空缺容易出现扭曲,多项式次数较高的时候拟合更好,但计算繁琐且容易数值不稳定。模型和空间相关性的插值方法以GPS时间序列模型为基础,保留原模型化的趋势项、周期项、阶跃、同震和震后形变,根据周边GPS站的噪声分布重构空缺处的噪声,尽可能使空缺值接近真实值,但重构的噪声仅包含主要成分,比真实误差的离散度小。
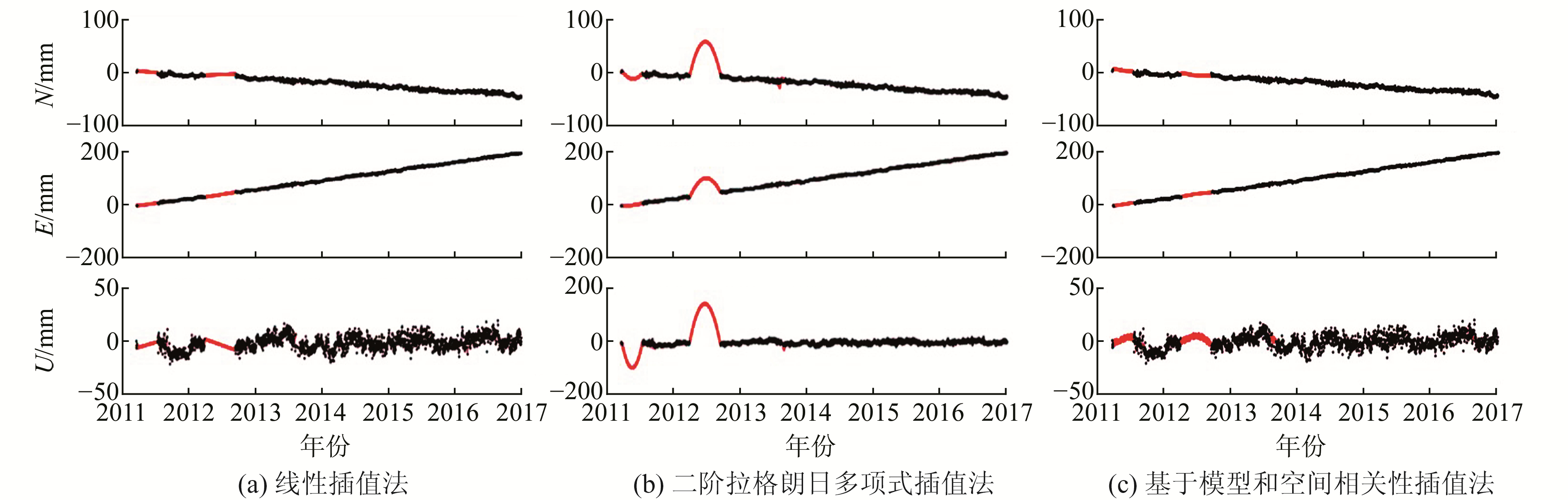
|
图 5 3种空缺插值方法对比 Fig. 5 The comparison among three interpolation methods |

|
图 4 SNFG与其他GPS站的噪声空间相关性及与距离的关系 Fig. 4 The correlation of noise among SNFG and other sites, and its relation with distance |
GPS速度是研究板块运动、地壳形变等的重要手段[14-15],而周期性形变的获取对于理解海洋潮汐负载、大气负载、地下水负载等各类周期性地球物理过程具有重要意义[7, 12]。为了分析空缺和插值方法对速度、周期项的影响,设计2组实验。由于SNAK站数据完整率最高,达99.81%,将该站作为已知真值,删除数据模拟空缺。方案1:模拟随机离散空缺,空缺率分别为10%、20%、…、90%共9种情况(编号A1~A9);方案2:模拟长空缺0.5 a、1 a、1.5 a、2 a、2.5 a和3 a共6种情况(编号B1~B6)。分别计算完整值和2组方案的速度值、年振幅和相位。
图 6(a)~(c)为方案1的结果,横坐标为A1~A9空缺形式,黑色实线为完整时间序列的计算值,作为真值,蓝圈为空缺的时间序列计算值,红圈为插值后的时间序列计算值,RMS值为空缺和插值的计算差异值RMS。可以看出,离散的空缺对速度的计算影响非常小。从年周期振幅的差异来看,空缺和插值的水平振幅基本一致,垂向振幅差异略大,垂向以周期性运动为主,空缺较多会影响周期振幅的计算,影响大小与振幅大小有关。从年周期的相位来看,空缺超过70%时相位差别非常大。无论速度、振幅和相位,空缺率与差异大小没有直接关系,说明离散空缺能一定程度上保留原始时间序列形态。

|
图 6 2组实验方案的速度、年周期振幅和相位对比 Fig. 6 The comparison of the velocity, the annual amplitude and the annual phase for two set of experiments |
图 6(d)~(f)为方案2中B1~B6空缺形式相应的计算结果, 图示与方案1一致。从速度差异来看,与真值的差异随空缺加长而变大,特别是N、U方向。在振幅和相位上,空缺和插值与真值差异都较大,相位上空缺和插值差异较小,超过0.5 a的空缺对速度、振幅和相位影响逐步变大。

|
图 7 2组实验方案噪声时间序列的功率谱 Fig. 7 The power spectrum of the interpolated noise time series for two set of experiments |
此外,对2组实验方案插值后的噪声时间序列进行频谱分析,进一步讨论基于模型和空间相关性的插值方法对噪声特性的改变。图 7为噪声时间序列的功率谱和对应的频谱在双对数坐标系下的分布。可以看出,在低频部分,离散空缺插值后的噪声比原始时间序列的功率谱值明显降低,插值比例增大;降低越多,高频部分的功率谱强度范围随着插值比例增加而有所收窄。这说明离散空缺的重构噪声包含了大部分高频噪声和强度降低的低频噪声。长空缺插值的噪声功率谱变化差异较小,噪声特性更稳定。
应用最小二乘求拟合功率谱的斜率,从而得到谱指数。为避免白噪声占主导的高频部分和f= 1/(14 d)的噪声谱峰值影响拟合结果[8],仅采用f < 1/(15 d)的频率和相应功率谱求得谱指数。表 1显示,噪声时间序列分布在-1~0之间,说明噪声时间序列具有白噪声和有色噪声。方案1的谱指数随着空缺比例升高而增大,说明离散空缺的插值损失了有色噪声成分,空缺率为90%时,插值的噪声时间序列接近白噪声。方案2的长空缺谱指数略低于原始值的谱指数,说明长空缺插值仅损失少量有色噪声。
|
|
表 1 2组实验方案的噪声时间序列谱指数 Tab. 1 The spectrum index of the interpolated noise time series for two set of experiments |
1) 本文提出改进的基于模型和空间相关性的插值方法,其效果优于线性插值和拉格朗日插值法,可以更好地处理长、短空缺的插值。GPS时间序列与模型的拟合度越好,噪声空间相关性越高,插值效果越好。
2) 基于空间相关性方法,利用周边GPS站的噪声来构建坐标时间序列空缺处的噪声,一方面具有一定的边际效应,即网中间空间相关性更强,网边缘空间相关性较弱;另一方面,站点越多,可靠性越强,抗差能力强,被质量差的观测数据污染的可能性较小。
3) 空间相关性分析显示,共模噪声具有较强的空间相关性,而相关性随距离而减弱,E方向相关性最强,N方向次之,U方向最弱。相关性弱的站点一般存在未模型化的局部运动,比如延安新城改造引起SNYA站的形变,略阳滑坡引起SNLY站的形变,导致这2个站的噪声空间相关性较弱。因此,利用空间相关性分析也有助于GPS站点局部运动的发现和分离。
4) 离散空缺对速度影响非常小,对年周期振幅影响与振幅大小相关,超过70%的空缺对相位影响非常大。而长空缺对于时间序列内部性质的保持损害较大,超过0.5 a的长空缺对速度、周期项影响较大。高比例的离散空缺和超过0.5 a的长空缺对周期项性质的影响较大,因此,基于GPS研究周期性的地球物理过程必须考虑此类空缺对周期性参数的影响。
5) 从噪声特性来看,离散空缺比长空缺对噪声信号强度和噪声类型损害更大。离散空缺插值后的噪声特性在低频部分降低了强度,插值比例越高降低越多,高频部分的功率谱范围随着插值比例增加而有所收窄。随着插值比例增高,谱指数增大,有色噪声比例降低,逐渐接近白噪声。长空缺插值的噪声功率谱变化差异较小,谱指数略小一点,仅损失少量有色噪声。
| [1] |
黄立人. GPS基准站时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33 (Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33)
(  0) 0) |
| [2] |
符养.中国大陆现今地壳形变与GPS坐标时间序列分析[D].上海: 中国科学院上海天文台, 2002 (Fu Yang. Present-Day Crustal Deformation in China and GPS-Derived Coordiante Time Series Analysis[D]. Shanghai: Shanghai Astronomical Observatory, CAS, 2002)
(  0) 0) |
| [3] |
武艳强, 黄立人. 时间序列处理的新插值方法[J]. 大地测量与地球动力学, 2004, 24(4): 43-47 (Wu Yanqiang, Huang Liren. A New Interpolation Method in Time Series Analyzing[J]. Journal of Geodesy and Geodynamics, 2004, 24(4): 43-47)
(  0) 0) |
| [4] |
Dong D N, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3)
(  0) 0) |
| [5] |
邱荣海, 成英燕, 王虎, 等. 奇异谱迭代区间四分法在GPS坐标时间序列插补中的应用[J]. 大地测量与地球动力学, 2015, 35(6): 1017-1020 (Qiu Ronghai, Cheng Yingyan, Wang Hu, et al. The Interpolation Application of Interval Quartering Algorithm of Singular Spectrum Analysis Iterative in GPS Coordinate Time Series[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 1017-1020)
(  0) 0) |
| [6] |
Wang X M, Cheng Y Y, Wu S Q, et al. An Effective Toolkit for the Interpolation and Gross Error Detection of GPS Time Series[J]. Survey Review, 2016, 48(348): 202-211 DOI:10.1179/1752270615Y.0000000023
(  0) 0) |
| [7] |
Xu C. Reconstruction of Gappy GPS Coordinate Time Series Using Empirical Orthogonal Functions[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(12): 9020-9033 DOI:10.1002/2016JB013188
(  0) 0) |
| [8] |
Nikolaidis R M. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: Univ of Calif, 2002
(  0) 0) |
| [9] |
Pearson K. Note on Regression and Inheritance in the Case of Two Parents[J]. Proceedings of the Royal Society of London, 1895, 58: 240-242 DOI:10.1098/rspl.1895.0041
(  0) 0) |
| [10] |
Guttman L. The Principal Components of Scale Analysis[M]. Princeton: Princeton University Press, 1950
(  0) 0) |
| [11] |
苏利娜, 丁晓光, 张彦芬, 等. 陕西连续GPS基准站坐标时间序列分析[J]. 大地测量与地球动力学, 2014, 34(5): 106-109 (Su Li'na, Ding Xiaoguang, Zhang Yanfen, et al. Study on Coordinate Time Series of Shaanxi GPS Reference Stations[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 106-109)
(  0) 0) |
| [12] |
Dong D N, Fang P, Bock Y, et al. Anatomy of Apparent Seasonal Variations from GPS Derived Site Position Time Series[J]. Journal of Geophysical Research Atmospheres, 2002, 107(B4)
(  0) 0) |
| [13] |
Tian Y F, Shen Z K. Extracting the Regional Common-mode Component of GPS Station Position Time Series from Dense Continuous Network[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(2)
(  0) 0) |
| [14] |
Gan W J, Zhang P Z, Zheng K S, et al. Present-Day Crustal Motion within the Tibetan Plateau Inferred from GPS Measurements[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B8)
(  0) 0) |
| [15] |
Bock Y, Melgar D. Physical Applications of GPS Geodesy: a Review[J]. Reports on Progress in Physics, 2016, 79(10)
(  0) 0) |
2. Institute of Geology, CEA, A1 Huayanli, Beijing 100029, China;
3. Institute of Earthquake Forecasting, CEA, 63 Fuxing Road, Beijing 100036, China;
4. Surveying and Mapping Engineering Institute of Yunnan Province, 39 West-Hongshan Road, Kunming 650033, China
 2019, Vol. 39
2019, Vol. 39

