GPS台站时间序列相对于其他空间大地测量技术呈现出明显的非线性变化，这些特征有助于研究台站非线性运动的物理机制，进而改正各种误差模型^[1]。为此，本文基于主成分分析法(PCA)，将全球GPS台站坐标残差时空矩阵分解成若干正交成分，分析和评估时间序列中各种非线性变化特征和统计规律，提取各分量坐标时间序列主分量的噪声特性、周年特性和季节特性，为进一步分析台站非线性变化机制奠定基础。

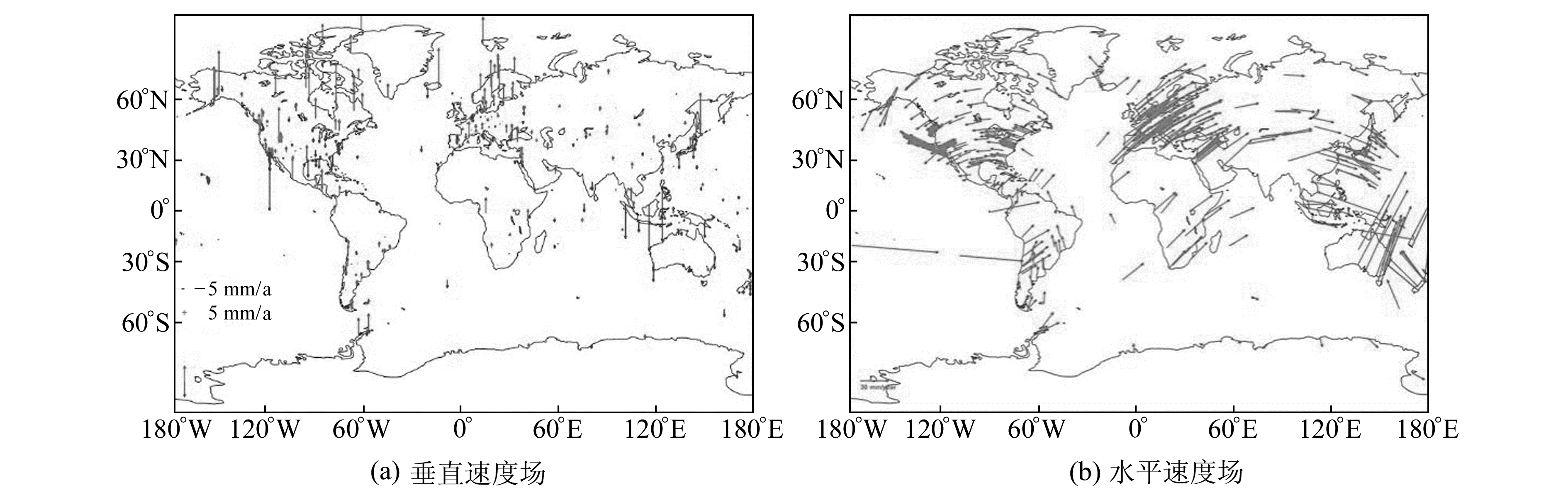
1 基于主成分分析法的台站时间序列分析 1.1 台站时间序列特征

理想情况下，GPS台站时间序列的噪声特性应表现为纯白噪声，然而由于地球物理效应及与GPS技术相关的系统误差，会产生潜在的有色噪声，如站点不稳定性导致闪烁噪声和随机游走噪声^[2]。连续GPS台站测量可以检测地壳的水平运动和垂直运动^[3]。图 1给出了GPS台站在水平和竖直方向的坐标速度场，图中显示了形式精度优于0.3 mm/a的台站，该速度场及其所反映出的板块运动整体情况与其他学者结果一致^[4]。大气压负荷、非潮汐海洋负荷和水文负荷与GPS台站垂直位移强相关^[5]，GPS数据处理模型的不完善及未模型化的GPS系统误差也可能导致虚假的非线性位移，包括电离层延迟高阶项、大气潮汐、海洋潮汐、对流层延迟处理方式等^[6]。因此，在台站坐标时间序列的模型化拟合过程中，应最大限度地减少参数个数，并选择合适跨度的数据序列进行拟合，以提高拟合参数的精度^[7]。

1.2 主成分分析法机理

PCA方法的数学原理和具体步骤如下。

1) 降维思想。PCA采用降维的思想，即将原有的多个属性转化为少数综合属性，已有属性通过适当的线性组合变换成相互独立的新属性，让数据本身体现出“空间响应均匀分布”特性。

设X是m×n矩阵，x_i为其元素，将X视为n个m维点的集合(对坐标残差序列来说，n代表台站数，m代表时间序列)，寻找一个k维空间(k < n)，使得原始数据点与X内所有数据点在k维空间中的投影点最接近，从而可以用得到的这些投影点来描述m个原始数据点，保证信息损失最小。

当k=1时，挑选一条过原点的直线，使原始数据点与到该直线上的投影最接近，记该直线为L₁，其单位向量为u₁，则x_i到L₁的投影为x_i^T u₁，所谓接近的准则是误差平方和$\sum\limits_{i = 1}^n \|{\mathit{\boldsymbol{x}}_i} - \left( {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right){\mathit{\boldsymbol{u}}_1}\|{^2}$达到最小。由勾股定理，有：

$ \begin{array}{*{20}{l}} {\quad \sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{x}}_i} - \left( {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right){\mathit{\boldsymbol{u}}_1}} \right\|}^2}} = }\\ {\sum\limits_{i = 1}^n {\left( {{{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|}^2} - {{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right\|}^2}} \right)} = }\\ {\sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|}^2}} - \sum\limits_{i = 1}^n {{{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right\|}^2}} } \end{array} $

(1)

由于$\sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|}^2}} $固定，上式的最小化问题即是使$\sum\limits_{i = 1}^n {{{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right\|}^2}} $最大化，利用矩阵表示则是求u使得u ^TX ^TXu最大。由二次型极值的性质可知，最大值就是X ^TX的最大特征值λ₁，达到这个最大值的u就是λ₁所对应的特征向量u₁，由此决定的L₁就是对数据具有最优拟合的一维空间。

然后进行二维空间拟合，求一个与u₁正交的单位向量u₂，由u₁和u₂产生二维空间，作m个点到这个二维空间的投影，使得这些投影点与原始数据点最接近，满足u ₁^T u₂=0的单位向量u₂使得$\sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{x}}_i} - \left( {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right){\mathit{\boldsymbol{u}}_1} - \left( {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_2}} \right){\mathit{\boldsymbol{u}}_2}} \right\|}^2}} $达到最小。同样由勾股定理得：

$ \begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{x}}_i} - \left( {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right){\mathit{\boldsymbol{u}}_1} - \left( {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_2}} \right){\mathit{\boldsymbol{u}}_2}} \right\|}^2}} = }\\ {\sum\limits_{i = 1}^n {\left( {{{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|}^2} - {{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right\|}^2} - {{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_2}} \right\|}^2}} \right)} = }\\ {\sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|}^2}} - \sum\limits_{i = 1}^n {{{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_1}} \right\|}^2}} - \sum\limits_{i = 1}^n {{{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_2}} \right\|}^2}} } \end{array} $

(2)

上式达到最小即是$\sum\limits_{i = 1}^n {{{\left\| {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_2}} \right\|}^2}} $达到最大，u₂即为X^TX第二大特征值所对应的特征向量。

依此类推，若设X ^TX的特征值λ₁>λ₂>…>λ_k>0，则其对应的标准正交特征向量分别为u₁，u₂，…，u_k。可以得到结论：对任意k(0 < k < n)，在所有可能的k维子空间，以X ^TX的前k个标准正交特征向量u₁，u₂，…，u_k张成的子空间，使x₁，x₂，…，x_n与其在子空间上的投影具有最小误差平方和。

2) 主成分对原始数据的恢复。记y_i= Xu_j, j=1, 2, …, k, 表示X的k个主成分，用矩阵表示为：

$ \mathit{\boldsymbol{Y}} = \left[ {{\mathit{\boldsymbol{y}}_1},{\mathit{\boldsymbol{y}}_2}, \cdots ,{\mathit{\boldsymbol{y}}_k}} \right] = \mathit{\boldsymbol{XU}} $

(3)

其中，U =(u₁, u₂, …，u_k)。由于

$ {\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{U}}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{XU}} = {\mathit{\boldsymbol{U}}^{\rm{T}}}\left( {\mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{U}}^{\rm{T}}}} \right)\mathit{\boldsymbol{U}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} $

(4)

主成分之间相互正交，且第j个主成分的模为$\sqrt {{\lambda _j}} $。由于特征向量U的正交性有X = YU^T，表示用主成分可恢复原始数据。若选择部分主成分对原始数据逼近，可得到最优化近似为：

$ {\mathit{\boldsymbol{x}}_i} \approx \sum\limits_{j = 1}^n {{\mathit{\boldsymbol{u}}_{ij}}} {\mathit{\boldsymbol{y}}_j},i = 1, \cdots ,k $

(5)

对任意p(1 < p < k)，逼近误差平方和为：

$ \begin{array}{l} {d_p} \buildrel \Delta \over = \sum\limits_{i = 1}^k {{{\left\| {{\mathit{\boldsymbol{x}}_i} - \sum\limits_{j = 1}^p {{\mathit{\boldsymbol{u}}_{ij}}} {\mathit{\boldsymbol{y}}_j}} \right\|}^2}} = \sum\limits_{i = 1}^k {{{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|}^2}} - \\ \;\;\;\;\sum\limits_{i = 1}^k {\sum\limits_{j = 1}^p {{{\left( {\sqrt {{\lambda _j}{\mathit{\boldsymbol{u}}_{ij}}} } \right)}^2}} } = {\mathop{\rm tr}\nolimits} \left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right) - \\ \sum\limits_{j = 1}^p {{\lambda _j}} \sum\limits_{i = 1}^k {\mathit{\boldsymbol{u}}_{ij}^2} = \sum\limits_{i = 1}^k i - \sum\limits_{j = 1}^p {{\lambda _j}} = \sum\limits_{j = p + 1}^k {{\lambda _j}} \end{array} $

(6)

式中，tr(X ^TX)表示X的总变差，λ_j表示主成分y_j对数据X的变差贡献，$\sum\limits_{j=1}^{p} \lambda_{j}$表示前p个主成分对数据X的总变差贡献率。从数据恢复损失信息最小来说，用主成分逼近是最优的。

3) 主成分计算。采用经典正交分解的方法计算主成分。首先要对数据矩阵X进行中心化处理，将X转化成一个列均值为0的中心化矩阵。计算X的协方差阵B的特征值λ₁>λ₂>…>λ_k>0及其对应的标准正交特征向量u₁, u₂, …, u_k，B矩阵及其谱分解表示为：

$ \boldsymbol{B}=\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}=\boldsymbol{U} \mathit{\pmb{\Lambda}} \boldsymbol{U}^{\mathrm{T}} $

(7)

其中，U =(u₁, u₂，…，u_k)，Λ =diag(λ₁, λ₂, …, λ_k)。计算主成分对总变差的累积贡献率：

$ {\alpha _p } \buildrel \Delta \over = \sum\limits_{i = 1}^\rho {{\lambda _i}} /\sum\limits_{i = 1}^k {{\lambda _i}} $

(8)

与已选定的累积贡献率c进行对比，确定使α_p>c最小的p值。计算p个主成分：

$ \boldsymbol{y}_{j}=\boldsymbol{X} \boldsymbol{u}_{j}, j=1,2, \cdots, p $

(9)

对GPS台站残差时间序列组成的时空矩阵X(m个历元n个站点组成的m×n阵，不失一般性，设m＞n)进行经典正交分解或奇异值分解，获取协方差矩阵B的特征向量阵U、特征值对角阵Λ，其中U和Λ均为n×n阵。主成分A表示为：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}(i,j) = \sum\limits_{k = 1}^n {{a_k}} (i){\mathit{\boldsymbol{u}}_k}(j)},\\ {(i = 1,2, \cdots ,m;j = 1,2, \cdots ,n)} \end{array} $

(10)

对特征值对角阵Λ进行降序排列并重排主成分以及特征向量，通过探查每个主成分特征向量的空间响应，选择特征向量具有空间统一响应的主成分来进行分析。

2 实验验证和精度评估 2.1 数据准备

根据He等^[8]利用4种技术得到的多年SINEX周(日)解以及全球并置站信息，引入方差分量估计加权方法，建立大型综合法方程系统，解算综合地球参考框架和地球定向参数时间序列。基于自主研发的综合软件STRF进行调优和自动化处理，生成J2005.0时刻的台站坐标时间序列。

PCA方法的核心是对数据进行正交分解，而正交分解要求时空数据矩阵连续无间断。因此，本文选择数据缺失低于15%、数据跨度10 a以上的GPS台站进行坐标时间序列分析，代表性GPS台站共299个，时间序列采样间隔为7 d。选择的GPS台站中，北美和欧洲西部最为密集，赤道附近台站数量较少，南北半球分布不均^[9]。

2.2 台站时间序列特征提取 2.2.1 时间序列数据预处理

大部分GPS台站的时间序列都存在明显跳变和间断点^[10]，会影响模型解算的精度和可靠性。在分析GPS台站坐标序列时，需要同时在时域和频域来研究其全貌和局部性质，从而更加有效地探测GPS台站坐标时间序列所含的非线性周期信息。因此，首先要对选择的GPS台站残差坐标时间序列进行数据预处理^[11]。

广义离群检测算法GESD (generalized extreme studentized deviate)可以探测跳变的时间点，检验服从近似正态分布的一个单变量数据集中的一个或多个粗差。本文采用小波变换结合广义离群检测算法，将时间序列中含有跳变的GPS台站坐标周解从原始坐标时间序列中剔除。同时，时间序列趋势项通常称为台站运动速度，其中异常的水平速度可能与台站的稳定有关，可对比推测可能存在的漂移运动^[12]。本文对有明显趋势项的台站进行去趋势处理并进行对比分析。

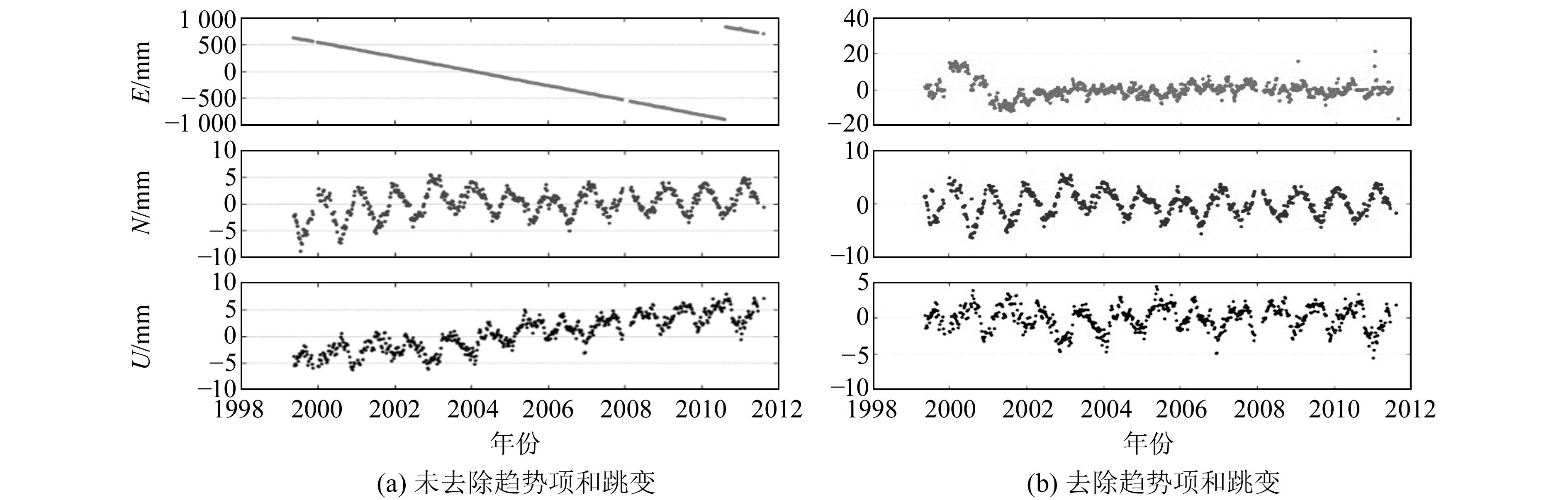
以AZCN站为例，设其未发生跳变，经过综合后得到的台站残差序列如图 2所示，可以看出，影响了2006~2010年的结果。如图 2(a)中，3个方向均存在显著的线性项特征，为此，将该站在约化儒略日55 425.0前后的站坐标进行分段处理，去除趋势项和跳变，解算后的时间序列如图 2(b)。对比发现，时间序列变得更平稳，进而周期性分析将更加可靠。

图 3为CHPI站去除趋势项前后的时间序列，可以看出，其在东西方向表现出明显的线性趋势项，推测可能存在水平漂移运动；垂向坐标时间序列也存在较小的整体趋势，这可能与该地区的地下水变化、台站稳定性和其他未知效应有关。扣除线性趋势项后(图 3(b))，整体变化和周期项信号更加突出。

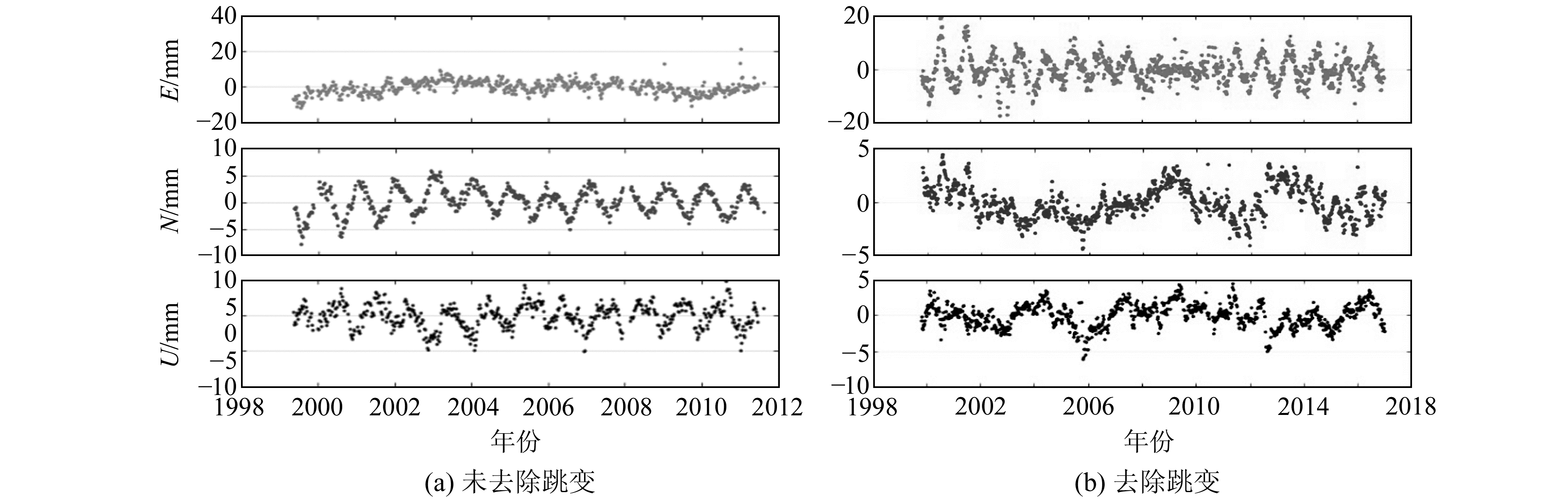
BJFS站是研究中国大陆及其邻近地区水平位移场的核心站之一(图 4)。可以看出，BJFS站水平方向的波动比垂直方向大，说明该台站垂直方向比水平方向稳定。其中南北向振幅约为-10~10 mm，东西向约为-20~40 mm；数据预处理之后，南北向振幅约为-5~5 mm，东西向约为-20~20 mm，垂直方向变化不大。2015-12南北、东西向存在微小跳变，参考相关资料可以推测，跳变是由于接收机和天线更换及数据处理中GPS卫星截止高度角改变所致。

为完成PCA对时空数据矩阵的正交分解，需要对时间序列中缺失的数据进行最小二乘内插补齐，获取3组完整的初始时空数据矩阵。通过对所有10 a以上较连续GPS台站时间序列的分析和探测，消去其中存在的跳变、线性趋势项和野值，弥补缺失历元数据，为周期项特征探测和分析准备好“干净”的数据。

2.2.2 用主成分分析方法分析时间序列

对预处理后的时空矩阵进行主成分分析，每组数据分别计算299个主成分、空间特征向量及主成分特征值。由于PCA方法的特性，在GPS台站坐标时间序列中提取主成分分量是独立的，因此可以对每个方向的分量进行特征提取。

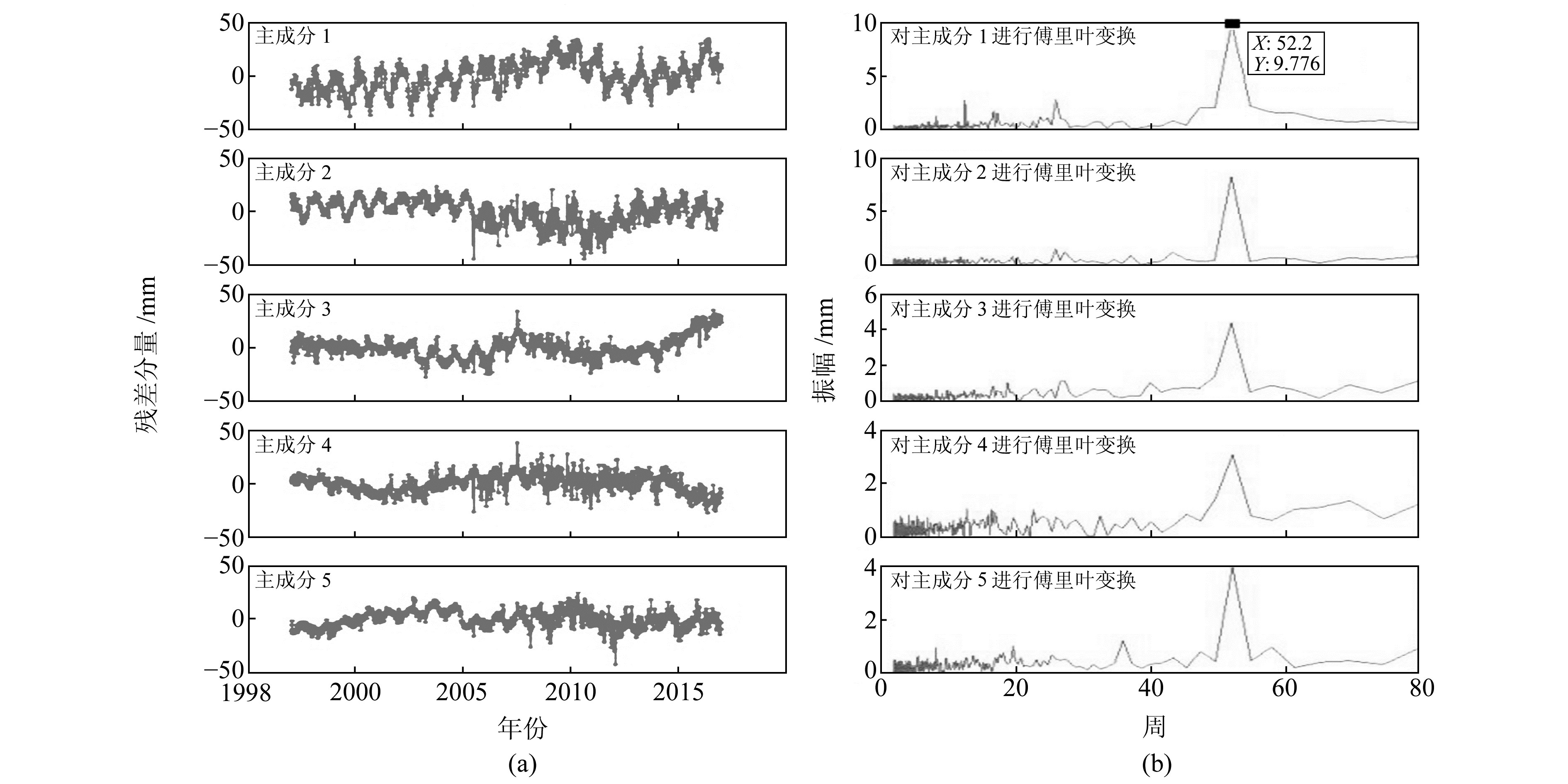
3个方向的贡献率及主分量统计见表 1，主分量对应的空间向量表示的是时空数据的空间相应特征——东西、南北和垂向的坐标时空矩阵第1主成分贡献率分别达到10%、12%和9 %，第2主成分的贡献率达到6%、7%和7%，其他主成分的贡献率更低。由此可见，越靠前的主成分分量越占据主导地位。分别对各主成分分量进行傅里叶分析，提取周期项，得到图 5~7。表 2统计了台站3个方向主成分的主要周期项。

可以看出，大部分台站在3个方向上的主要周期项均为周年项，同时垂直方向的第1主分量存在半年和季节性变化周期；另外南北方向的第1主分量、东西方向的第4分量也存在半年周期项。幅度方面，东西方向的幅值远大于另外2个方向，前3个主分量的周年项振幅依次为41.7 mm、25.9 mm和11.2 mm，说明GPS台站主要表现出东西方向的位移。根据幅度值可以看出，3个方向各主分量的幅值基本符合从大到小的排列规律，与贡献率值基本吻合。

GPS台站时间序列的垂直方向表现出明显的季节性。由于目前的地球参考框架模型仅考虑台站的线性运动情况，因此台站的周期信号均被残差序列所吸收。造成台站周期信号的可能原因较多，如地表温度变化、大气潮汐效应、陆地水和海洋环流等地理现象或者观测技术系统误差。从图 6看出，东西方向的周期性运动振幅小于其长期项运动振幅，水平方向的主要分量中1 a周期项最为突出。

从上面的分析可以看出，目前线性STRF地球参考框架没有考虑非线性的周期运动和震后形变，这些信息就包含在台站坐标的残差序列中。GPS台站坐标残差序列有明显的周年项和季节项，这些周期项可能是由地球物理现象如地球表面物质随时间变化产生的负荷效应(如海潮、大气潮汐效应、积雪、土壤水、海洋非潮汐影响、地表温度变化、陆地水和海洋环流等)引起的，也可能是因潮汐频率和GPS卫星轨道频率之间差异引起的长周期影响导致的海潮改正误差放大或GPS观测技术系统误差。从表 2看出，东西向的周期性运动振幅小于其长期项运动振幅，水平方向的主要分量中1 a周期项最为突出。

3 结语

本文利用全球299个具有10 a以上、观测较为连续的GPS台站数据，通过主成分分析法进行台站时间序列变化分析。结果表明，主成分分析法可以将时空矩阵分解成若干正交成分，有效提取时间序列中的周年项、半年项等周期项。在GPS台站东西向、南北向和垂向3个方向的周期性特征中，1 a周期具有一定的普遍性。另外大部分台站受板块运动影响，在东西向有较大的线性漂移速度。台站坐标残差序列信息研究及其结果分析对沉降或变形监测及趋势预报、地球物理相关方向研究和地球参考框架精度及GPS数据处理模型误差精度提高等具有重要的参考意义，为下一步寻找其机制、探讨其与地球物理现象的相关性奠定了基础。