2. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙市麓山南路932号,410083
海洋潮汐使得海水质量分布发生改变,并使固体地球产生弹性响应,称为海潮负荷(ocean tide loading,OTL)。海潮负荷在沿海地区对测站位移的影响可达数cm[1],在高精度测量工作中不能忽视。通常利用全球海潮模型与负荷格林函数褶积积分获取海潮负荷位移参数(振幅和相位)[2-3],但由于全球海潮模型在近岸浅水区域精度较差,直接采用全球海潮模型计算的某些沿海地区测站的海潮负荷位移差异可达1 cm以上[4]。许多学者研究了利用差分GPS和GPS精密单点定位(PPP)手段测定海潮负荷位移。前者测定海潮负荷位移需要一个或多个参考站点[5-6],参考站点需要使用海潮模型进行海潮负荷改正,且其稳定性受到诸多环境因素的影响,会引入更多误差。后者主要分为静态和动态2种方法。通过PPP单天解算,将海潮负荷位移参数同坐标参数一起估计的方法称为静态方法。由于每天只能得到一组估值,该方法将会平滑一些分潮(1/3日潮)信号[7-8]。从高采样率PPP坐标序列中分离海潮负荷信号的方法称为动态方法,可以直接反映短时间内的海潮负荷位移变化及一些振幅较小的分潮信号。目前相关研究主要从高采样率的动态PPP坐标序列中分离海潮负荷位移参数[9-11],其反演效果差于静态方法。虽然静态PPP定位精度相对高于动态PPP,但其采样率有所降低,且从静态PPP坐标序列中分离海潮负荷位移参数还未得到深入研究。
本文尝试从短期静态PPP结果中分离海潮负荷位移参数。首先采用香港地区11个测站的GPS观测数据,通过对GPS观测数据进行不同时长(1 h、2 h、3 h和4 h)的静态PPP解算获得不同采样率的坐标序列;然后利用调和分析[12]方法从4组PPP结果中分离海潮负荷位移参数;最后结合海潮模型改正值及其在PPP解算中的改正情况,综合分析短期静态PPP结果反演海潮负荷位移的效果。
1 研究方法 1.1 利用GPS PPP结果反演海潮负荷位移测站P处k方向的海潮负荷位移可表示为:
| $ \begin{array}{*{20}{c}} {{\eta _k}(P) = }\\ {\sum\limits_{i = 1}^8 {{f_i}} {H_{i,k}}(P)\cos \left( {{\sigma _i}t + {\chi _i} + {\mu _i} - {\varphi _{i.k}}(P)} \right)} \end{array} $ | (1) |
式中,ηk(P)为测站P处k方向的海潮负荷位移,fi和μi为交点因子和交点订正角,Hi, k(P)和φi, k(P)分别为测站P处分潮i在k方向的振幅和相位迟角,σi为分潮i角频率,χi为分潮i的参考时刻天文相角,t为世界时。其中,振幅和相位迟角为需求解的海潮负荷位移参数,其余参数可通过查表获得。通过GPS PPP技术可获得E、N、U方向的位移序列,对位移序列进行调和分析可求取8个潮波在E、N、U方向的海潮负荷位移参数。
1.2 GPS估值与海潮模型改正值差异比较全球海潮模型在中国近海地区精度不足,利用精度较高的区域海潮模型与全球海潮模型组合,可以提供精度更高的海潮负荷位移计算值。osu.chinasea.2010是包含中国东海和南海的高精度区域海潮模型[13],TPXO7.2是全球范围的高精度海潮模型[14-15]。利用osu.chinasea.2010海潮模型替换TPXO7.2全球海潮模型中的中国近海部分,得到osu.chinasea.2010+TPXO7.2组合海潮模型。然后利用SPOTL软件,通过组合海潮模型与负荷格林函数褶积积分,得到各个测站处的海潮负荷位移参数。将上述海潮负荷位移值作为模型值,综合分析GPS估值与模型值的均方根差异。吴志露等[9]发现,GPS估值与海潮模型值残差具有一致性,定义为“观测均方根误差”,该统计量可作为GPS测定海潮负荷位移参数的内符合观测精度:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;观测均方根误{差_{j,k}} = \\ {\left( {\frac{1}{N}\sum\limits_{n = 1}^N {{{\left| {{Z_{j.k \cdot n}} - {\mathop{\rm mean}\nolimits} \left( {{Z_{j,k,n}}} \right)} \right|}^2}} } \right)^{\frac{1}{2}}} \end{array} $ | (2) |
式中,mean(Zj, k, n)为潮波j、坐标分量k在所有测站(n=1,…,N)的GPS估值和模型值之间的残差均值。均方根误差Zj, k, n为:
| $ \begin{array}{l} {Z_{j,k,n}} = {A_{{\rm{GPS}}}}{\left( {\cos {\mathit{\Phi} _{{\rm{CPS}}}} + {\rm{i}}\sin {\mathit{\Phi} _{{\rm{CPS}}}}} \right)_{j,k,n}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{A_m}{\left( {\cos {\mathit{\Phi} _m} + {\rm{i}}\sin {\mathit{\Phi} _m}} \right)_{j,k,n}} \end{array} $ | (3) |
式中,A为振幅,Φ为相位迟角。
在k方向上,顾及8个分潮(4个半日潮波M2、N2、S2、K2,4个全日潮波K1、P1、O1、Q1)的总体均方根误差为:
| $ 总体均方根误差{_k} = {\left( {\sum\limits_{j = 1}^8 {{Z_{j,k,n}}} } \right)^{\frac{1}{2}}} $ | (4) |
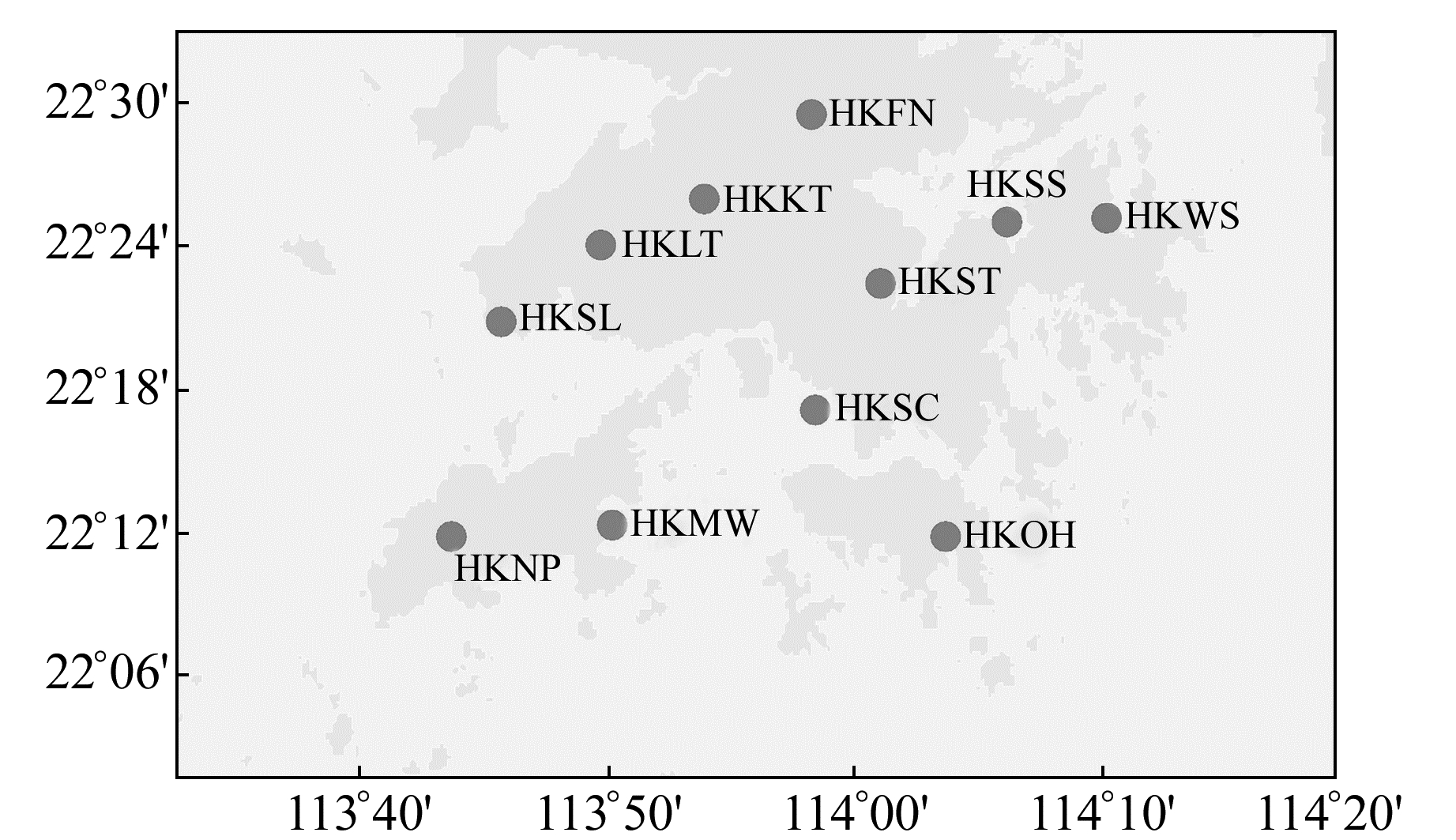
香港地区海岸线复杂,受海潮负荷影响明显。香港自2000年开始建设卫星定位参考网,目前已有18个连续运行参考站。采用香港地政总署测绘处(http://www.geodetic.gov.hk/smo/gsi/programs/tc/index.htm)提供的2013年卫星定位参考网GPS观测数据,选择观测数据较为完整的11个CORS进行研究,如图 1所示。
|
图 1 香港地区11个CORS分布 Fig. 1 The distribution of 11 CORS in Hong Kong |
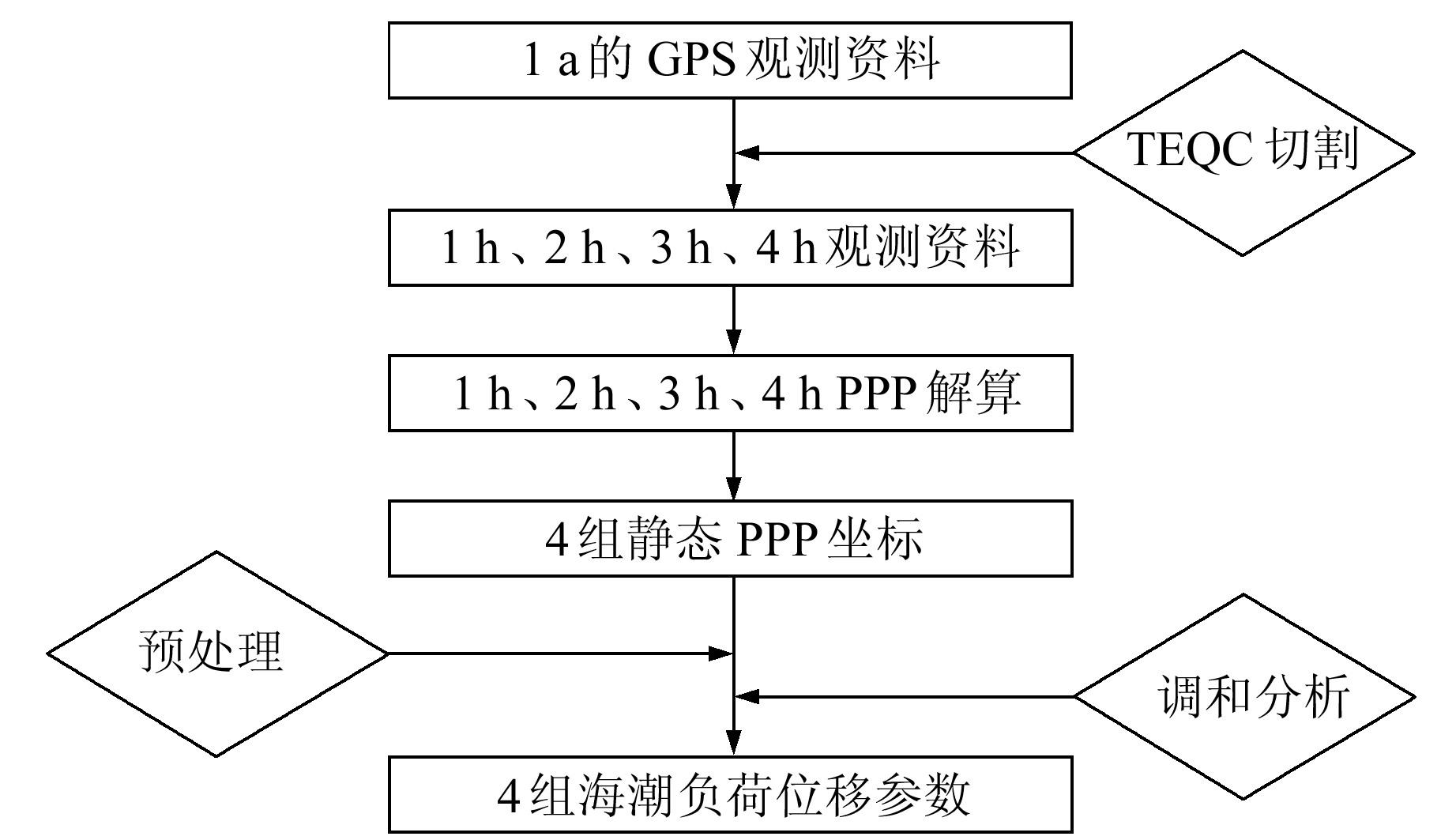
根据潮波调和分析的观点[12],为保证分潮信号可分离,潮汐观测时间间隔应小于分潮的半周期,并且可分离的2个分潮信号的频率差应满足瑞利准则,即Δf≥1/T,其中T为总的观测时间长度。在8个短周期潮波中,K2分潮周期最短,为11.967 2 h,因此观测时间间隔须小于5.983 6 h,而K2分潮与S2分潮、K1分潮与P1分潮的频率最为接近,将4个分潮信号分离至少需要189 d的观测时间。考虑到静态PPP需要0.5 h以上的观测时间才能收敛稳定,为保证解算精度,本文采用时间长度为1 a,观测间隔为1 h、2 h、3 h和4 h的GPS数据进行静态PPP解算,可以得到该观测时间间隔的4组坐标时间序列。GPS数据处理流程如图 2。
|
图 2 GPS数据处理流程 Fig. 2 The flow chart of GPS data processing |
1) GPS观测文件处理。使用TEQC软件将1 a的GPS观测文件分别切割为1 h、2 h、3 h、4 h间隔的4组观测文件。
2) GPS数据解算。PPP解算由Bernese V5.0软件处理完成。数据采样率为300 s,卫星截止高度角为10°,其余参数设置如表 1所示。采用上述解算方法对4组观测文件分别进行静态PPP解算,得到4组解算结果。PPP解算结果为地心三维坐标(X,Y,Z),需将其转换为站心地平坐标(E,N,U)。
|
|
表 1 PPP解算参数设置 Tab. 1 The parameters of PPP solution |
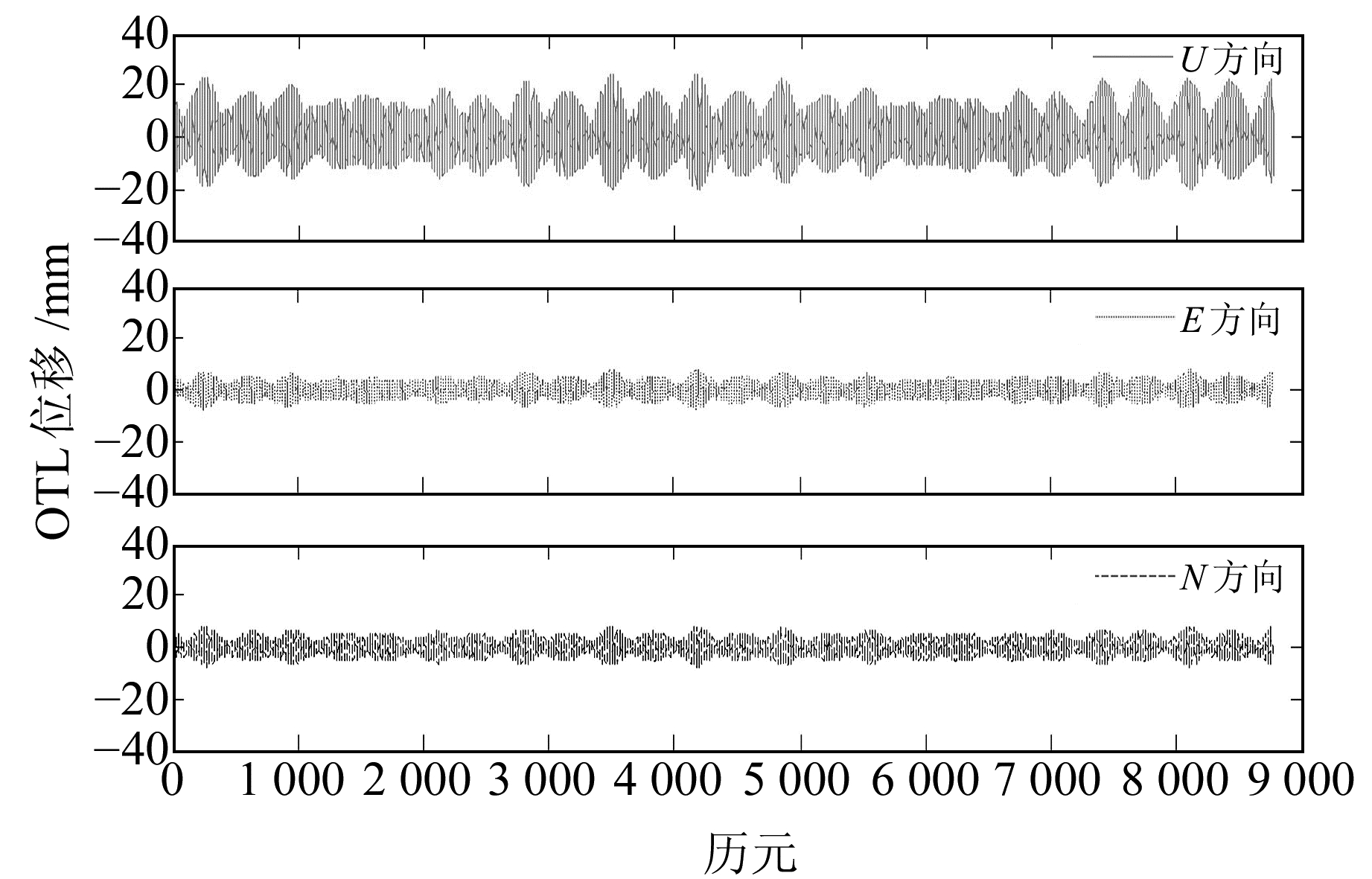
3) PPP结果预处理。分析测站的GPS数据发现,HKLT测站存在1 a观测数据缺失,本文坐标序列中的不连续处保留空值,不参与海潮负荷位移参数估计。静态PPP解算精度为cm级,PPP解算得到的坐标序列值可能出现较大粗差,而香港地区E、N方向海潮负荷位移的影响为mm级,U方向为cm级,如图 3所示,因而考虑对U、E、N 3个方向的坐标值施加阈值。对U、E、N 3个方向分别取500 mm、200 mm、200 mm阈值,高于阈值的坐标值被赋以阈值。
|
图 3 TPXO7.2+osu.chinasea.2010海潮模型估算HKSC测站海潮负荷位移变化 Fig. 3 Ocean tide loading displacements estimated by TPXO7.2+osu.chinasea.2010 tide model at HKSC |
4) 海潮负荷位移参数反演。利用调和分析方法提取4组坐标序列中的海潮负荷位移参数。
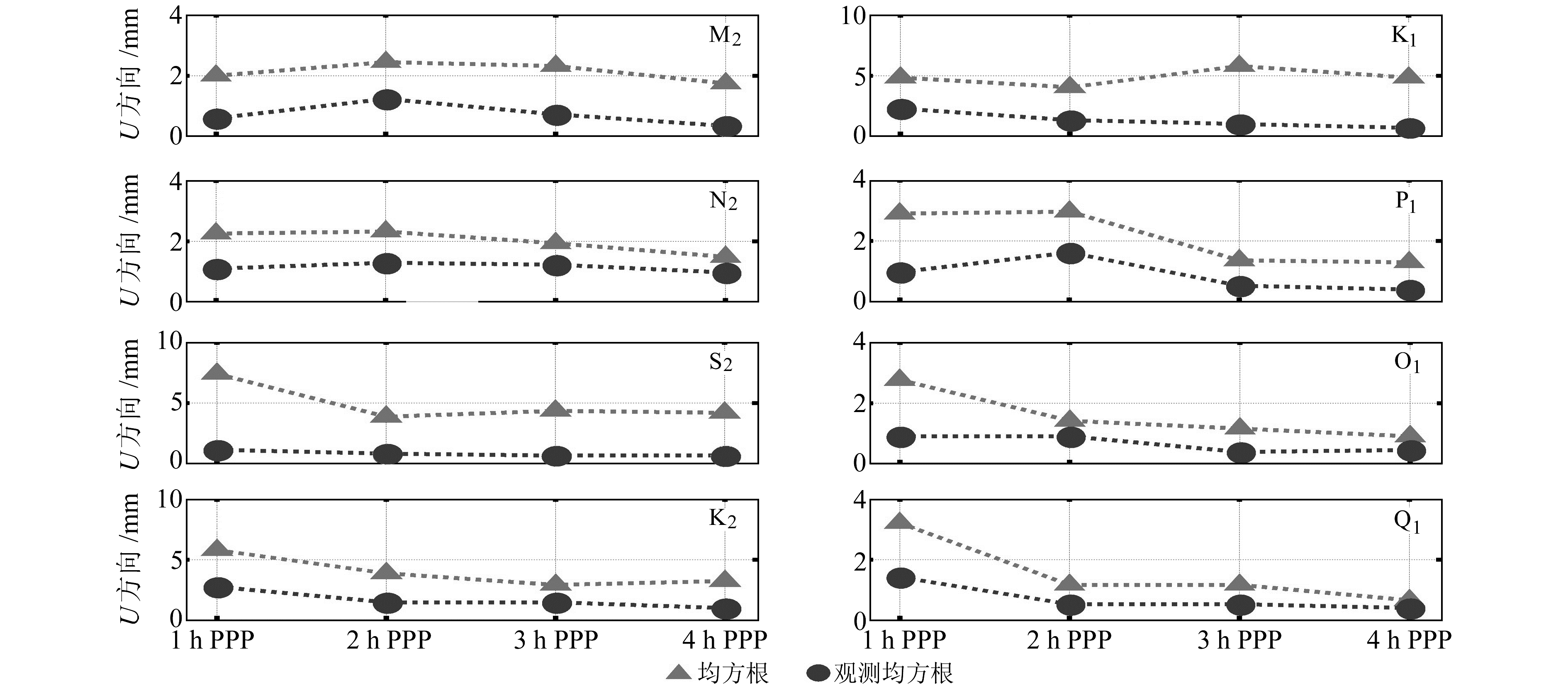
3 海潮负荷位移参数反演效果 3.1 GPS反演海潮负荷位移参数与海潮模型改正值一致性分析对每个CORS的4组PPP坐标序列进行调和分析,求取11个CORS的海潮负荷位移参数(振幅和相位),根据式(2)、式(3)分别计算PPP结果反演8个潮波U、E、N方向海潮负荷位移参数的均方根误差及观测均方根误差(图 4~6)。
|
图 4 PPP结果反演8个潮波U方向的均方根误差及观测均方根误差 Fig. 4 The RMS misfits and observed RMS misfits of 8 constituents measured by PPP in the U direction |
|
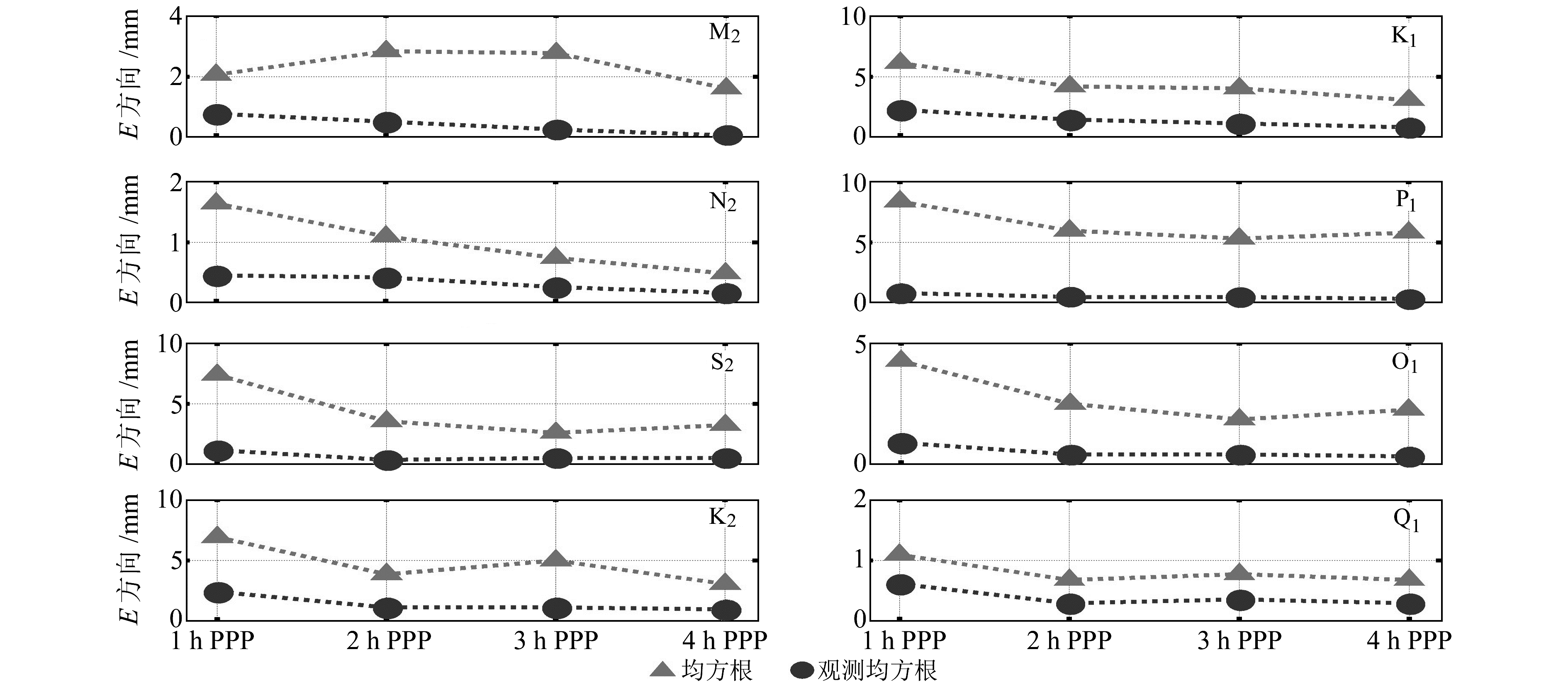
图 5 PPP结果反演8个潮波E方向的均方根误差及观测均方根误差 Fig. 5 The RMS misfits and observed RMS misfits of 8 constituents measured by PPP in the E direction |
|
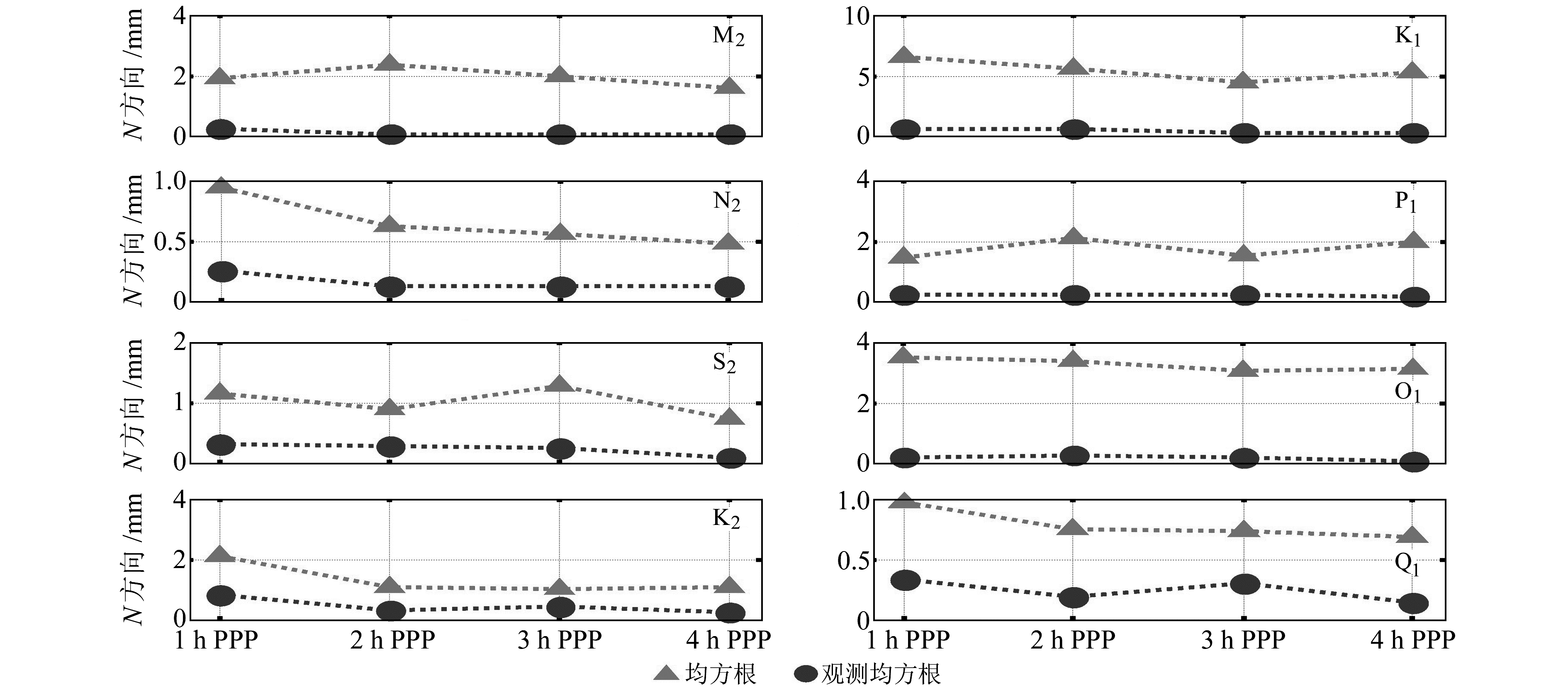
图 6 PPP结果反演8个潮波N方向的均方根误差及观测均方根误差 Fig. 6 The RMS misfits and observed RMS misfits of 8 constituents measured by PPP in the N direction |
图 4显示,在U方向上,PPP反演8个分潮的观测均方根误差基本在2 mm以内;K1、K2、S2分潮海潮负荷位移参数与海潮模型值均方根差异偏大,4组PPP反演结果与海潮模型值的最小均方根误差分别达到5 mm、3 mm、4 mm,其余分潮的最小均方根误差在1.8 mm以内;M2、N2、K1、P1、O1分潮上不同采样率PPP反演值均方根误差的差异为1~2 mm,K2、S2、Q1分潮上不同采样率PPP反演值均方根误差的差异为2 ~4 mm。
图 5显示,在E方向上,PPP反演8个分潮的观测均方根误差基本在1 mm以内;K1、P1、K2、S2分潮海潮负荷位移参数与海潮模型值均方根差异偏大,4组PPP反演结果与海潮模型值的最小均方根误差分别达到3 mm、5 mm、3 mm、3 mm,其余分潮的最小均方根误差在1.8 mm以内;M2、N2、O1分潮上不同采样率PPP反演值均方根误差的差异为1 ~2 mm,K2、S2、K1、P1、Q1分潮上不同采样率PPP反演值均方根误差的差异为2~5 mm。
图 6显示,在N方向上,PPP反演8个分潮的观测均方根误差基本在亚mm级;K1、O1分潮海潮负荷位移参数与海潮模型值均方根差异偏大,4组PPP反演结果与海潮模型值的最小均方根误差分别达到5 mm、3 mm,其余分潮的最小均方根误差在1.6 mm以内;8个分潮上不同采样率PPP反演值均方根误差的差异为1~2 mm。
根据式(4)计算4组PPP结果反演8个分潮的总体均方根误差及除去PPP反演值与海潮模型值相差稍大的分潮的总体均方根误差,如图 7所示。
|
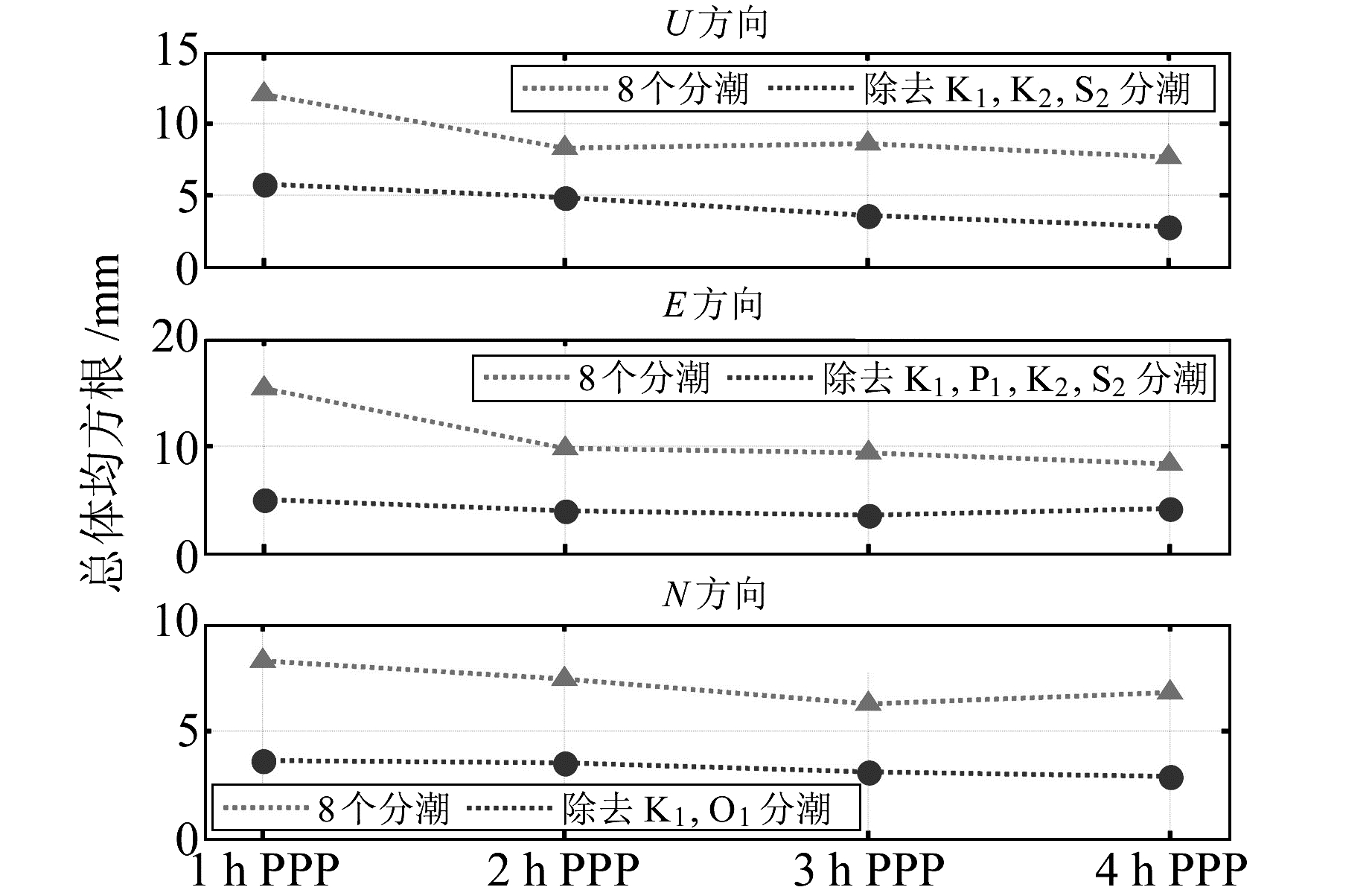
图 7 4组PPP结果测定OTL位移的总体均方根误差 Fig. 7 The sum RMS misfits of OTL displacements measured by 4 sets of PPP results |
图 7显示,顾及8个分潮,在U、E、N方向上不同采样率PPP反演值的总体均方根误差之间的差异分别达到约5 mm、7 mm和2 mm。除去PPP反演值与海潮模型值差异稍大的分潮,不同采样率PPP反演值的总体均方根之间的差异明显减小,分别约为2 mm、1 mm和1 mm。这表明,不同采样率PPP反演值之间的差异主要体现在GPS估值与海潮模型值差异较大的分潮上。目前,GPS轨道误差、多路径效应仍无法精确建模,这2种误差会对K1、K2潮波产生影响[14]。另外,与太阳有关的高阶电离层误差、对流层建模误差可能对S2潮波有影响[9]。在水平方向上,除K1、K2、S2分潮外,P1、O1分潮的GPS估值与海潮模型值相差稍大,与文献[11]采用1 a动态PPP反演效果相比也略大,这可能是由于静态PPP观测时间间隔相对较长,平滑了部分与这2个分潮相关的信号。
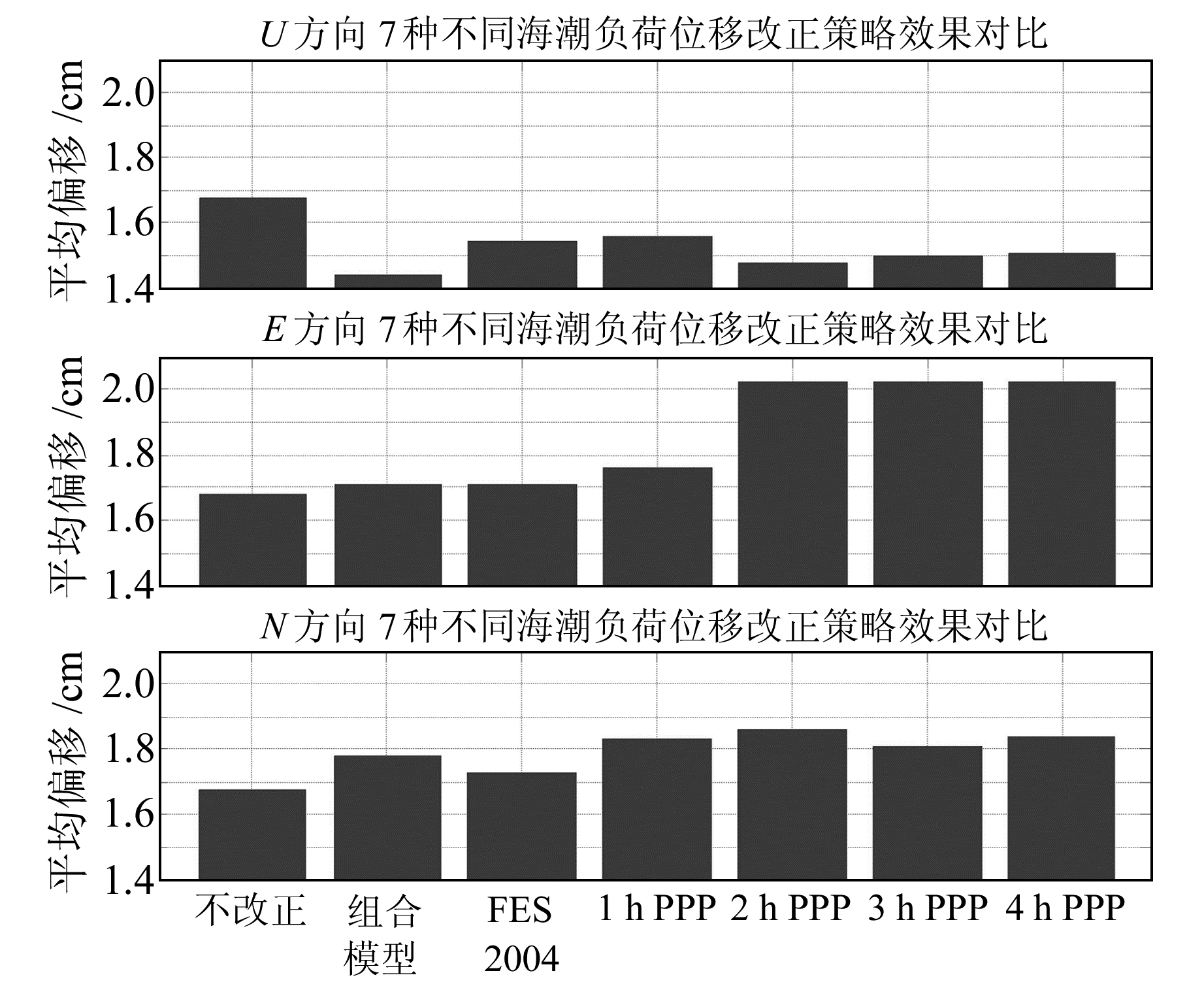
3.2 GPS PPP反演值改正海潮负荷位移效果11个测站的观测均方根误差基本在2 mm内,说明11个测站处GPS估值与海潮模型值残差具有区域一致性。选取其中HKFN测站来探究GPS PPP反演海潮负荷位移参数在PPP解算中的改正效果。海潮负荷位移影响具有较为明显的0.5 a、1 a周期性,本文解算HKFN测站的单天PPP解,然后将2013年第1~100 d的单天解进行平均,得到基本消除海潮负荷位移影响的精确参考坐标。考虑到8个短周期分潮的周期最小为11.96 h,因而6 h静态PPP解受到海潮负荷周期性影响。为分别探究组合海潮模型、全球海潮模型及GPS PPP反演值改正U、E、N方向海潮负荷位移的效果,采用7×3种策略对HKFN测站2013年第1~20 d的GPS数据进行66 h PPP解算:分别在U、E、N方向上,1)不加海潮负荷改正;2)加入osu.chinasea.2010+TPXO7.2组合海潮模型改正值;3)加入FES2004全球海潮模型改正值;4)加入1 h PPP结果反演值;5)加入2 h PPP结果反演值;6)加入3 h PPP结果反演值;7)加入4 h PPP结果反演值。将7×3组6 h PPP解算坐标减去参考坐标,可得到7×3种不同处理策略PPP解算坐标的平均偏移值,在U、E、N方向采取不同改正策略得到的坐标平均偏移如图 8所示,采取7×3种不同改正策略进行PPP解算的RMSE如图 9所示。
|
图 8 7种不同改正策略PPP解算的坐标偏移 Fig. 8 Coordinate displacements of PPP solution by using 7 different correction strategies |
|
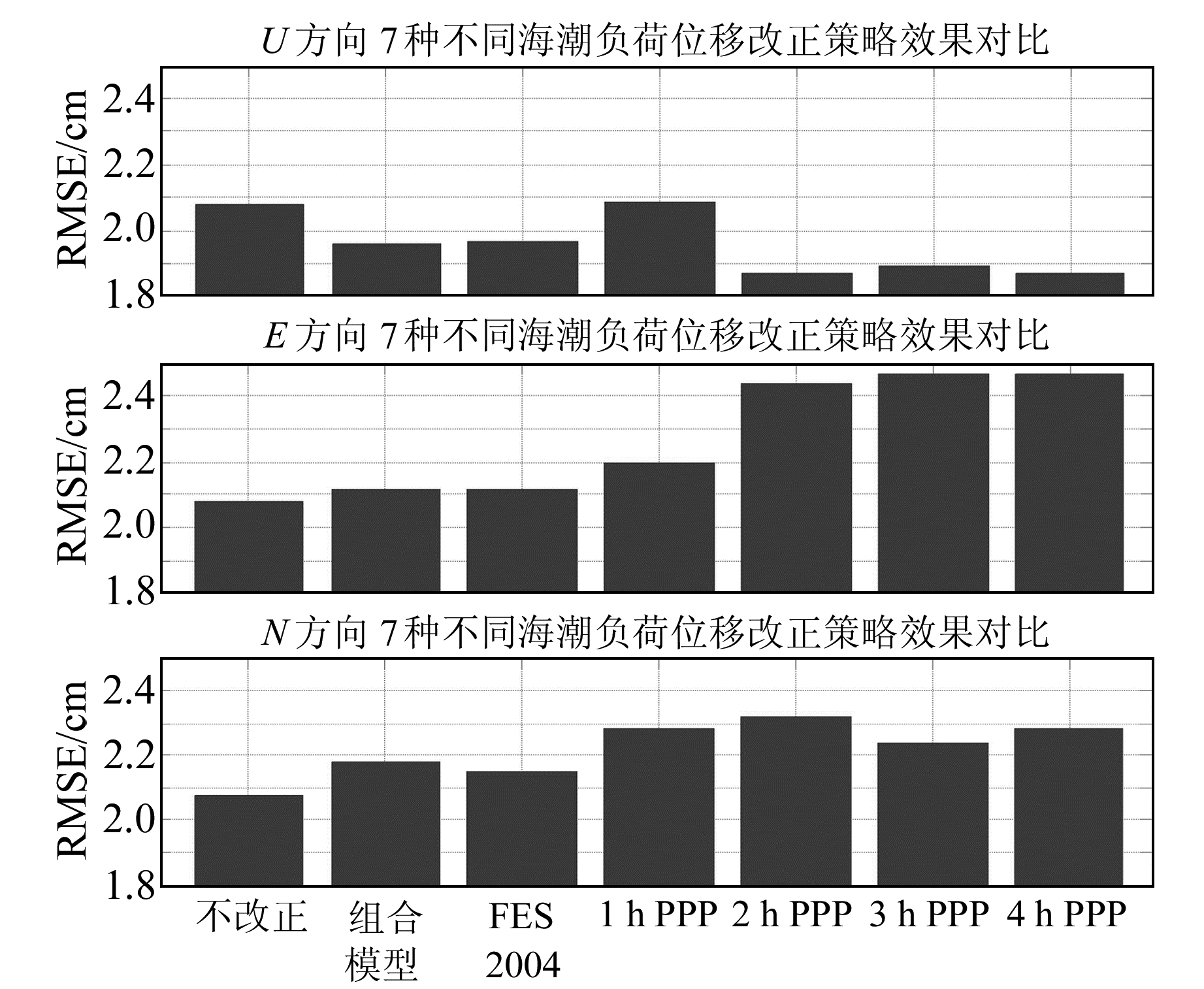
图 9 7种不同改正策略PPP解算的RMSE Fig. 9 RMSE of PPP solution by using 7 different correction strategies |
分析图 8和图 9可知:1)在U方向上,PPP反演值改正海潮负荷位移效果明显。从坐标偏移减小情况看,2 h PPP、3 h PPP、4 h PPP反演值改正效果优于全球海潮模型FES2004,稍差于osu.chinasea.2010+TPXO7.2组合海潮模型;从RMSE减小情况看,2 h PPP、3 h PPP、4 h PPP反演值改正效果优于全球海潮模型FES2004及osu.chinasea.2010+TPXO7.2组合海潮模型。综合坐标偏移及RMSE减小情况来看,2 h PPP反演效果最佳;1 h PPP的分辨率虽然较高,但其定位精度相对较弱,导致反演结果最差,其与海潮模型值的均方根差异也最大;3 h PPP、4 h PPP虽然精度提高,但分辨率降低,反演结果也稍弱。2)在E、N方向上,加入PPP反演值改正和海潮模型值改正后,坐标偏移及RMSE均扩大,但前者扩大更多,表明PPP反演E、N方向的海潮负荷位移效果差于海潮模型。所以,在区域内短期静态PPP反演垂向海潮负荷位移效果可优于全球模型,与组合海潮模型相比互有优势,但反演水平方向海潮负荷位移效果差于海潮模型。实验结果也表明,全球海潮模型在区域内还存有一定偏差,需要进一步精化。
4 结语在沿海地区,海洋潮汐负荷对GPS PPP的影响不可忽略,同时GPS PPP时间序列中也隐含了海潮负荷信号。本文尝试利用香港11个GPS测站1 a的观测资料,从短期静态PPP结果中求取海潮负荷位移参数并得到以下结论:
1) 与动态PPP反演结果相比,静态PPP反演O1、P1分潮水平方向的海潮负荷位移相对偏大。
2) 在U、E和N方向上,不同采样率PPP反演8个分潮的海潮负荷位移分别有5 mm、7 mm和2 mm的差异。
3) 静态PPP反演垂向海潮负荷位移效果优于全球海潮模型FES2004,但反演水平方向海潮负荷位移效果差于海潮模型。
总体来看,在对观测数据长度要求较低、计算量要求较少时,采用静态PPP结果可以有效地反演沿海地区垂向的海潮负荷位移变化,尤其是海岸线复杂、全球海潮模型适用性较差且GPS观测资料不充足时。
致谢: 感谢UNAVCO机构提供TEQC软件,感谢Agnew教授提供SPOTL软件,感谢香港特别行政区政府地政总署提供GPS观测数据。
| [1] |
刘经南, 张化疑, 刘焱雄, 等. GNSS研究海潮负荷效应进展[J]. 武汉大学学报:信息科学版, 2016, 41(1): 9-14 (Liu Jingnan, Zhang Huayi, Liu Yanxiong, et al. Progress of Ocean Tide Loading Inversion Based on GNSS[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 9-14)
(  0) 0) |
| [2] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [3] |
Farrell W E. Earth Tides, Ocean Tides and Tidal Loading[J]. Philosophical Transactions of the Royal Society of Biological Sciences, 1973, 274(1239): 253-259 DOI:10.1098/rsta.1973.0050
(  0) 0) |
| [4] |
赵红, 张勤, 黄观文, 等. 基于不同海潮模型研究海潮负荷对GPS精密定位的影响[J]. 大地测量与地球动力学, 2012, 32(5): 108-112 (Zhao Hong, Zhang Qin, Huang Guanwen, et al. Effect of Ocean Tide Loading on GPS Precise Positioning Based on Different Ocean Tide Models[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 108-112)
(  0) 0) |
| [5] |
Yun H S, Lee D H, Song D S. Determination of Vertical Displacements over the Coastal Area of Korea Due to the Ocean Tide Loading Using GPS Observations[J]. Journal of Geodynamics, 2007, 43(4-5): 528-541 DOI:10.1016/j.jog.2006.11.005
(  0) 0) |
| [6] |
Vergnolle M, Bouin M N, Morel L, et al. GPS Estimates of Ocean Tide Loading in NW-France:Determination of Ocean Tide Loading Constituents and Comparison with a Recent Ocean Tide Model[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 173(2): 444-458
(  0) 0) |
| [7] |
Allinson C R, Clarke P J, Edwards S J, et al. Stability of Direct GPS Estimates of Ocean Tide Loading[J]. Geophysical Research Letters, 2004, 31(15): 121-141
(  0) 0) |
| [8] |
King M A, Penna N T, Clarke P J, et al. Validation of Ocean Tide Models around Antarctica Using Onshore GPS and Gravity Data[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B8)
(  0) 0) |
| [9] |
吴志露, 刘焱雄, 何秀凤, 等. 基于近岸海岛GPS数据反演海洋分潮负荷影响[J]. 地球物理学报, 2017, 60(1): 61-69 (Wu Zhilu, Liu Yanxiong, He Xiufeng, et al. Inversion of Ocean Tidal Loadings of Marine Constituents Based on the GPS Measurements in the Offshore Islands[J]. Chinese J Geophys, 2017, 60(1): 61-69)
(  0) 0) |
| [10] |
郑凯, 马兰, 季伟, 等. 利用PPP反演海潮负荷位移参数[J]. 大地测量与地球动力学, 2015, 35(3): 485-489 (Zheng Kai, Ma Lan, Ji Wei, et al. Estimates of Ocean Tide Loading with PPP Displacements[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 485-489)
(  0) 0) |
| [11] |
张小红, 马兰, 李盼. 利用动态PPP技术确定海潮负荷位移[J]. 测绘学报, 2016, 45(6): 631-638 (Zhang Xiaohong, Ma Lan, Li Pan. Determination of Ocean Tide Loading Displacements Using Kinematic PPP[J]. Acta Geodaetica et Cartography Sinica, 2016, 45(6): 631-638)
(  0) 0) |
| [12] |
暴景阳, 许军. 卫星测高数据的潮汐提取与建模应用[M]. 北京: 测绘出版社, 2013 (Bao Jingyang, Xu Jun. Tide Analysis from Altimeter Data and the Establishment and Application of Tide Model[M]. Beijing: Surveying and Mapping Press, 2013)
(  0) 0) |
| [13] |
Lefèvre F, Provost C L, Lyard F H. How Can We Improve a Global Ocean Tide Model at a Regional Scale?A Test on the Yellow Sea and the East China Sea[J]. Journal of Geophysical Research Oceans, 2000, 105(C4): 8707-8725 DOI:10.1029/1999JC900281
(  0) 0) |
| [14] |
李大炜, 李建成, 金涛勇, 等. 利用验潮站资料评估全球海潮模型的精度[J]. 大地测量与地球动力学, 2012, 32(4): 106-110 (Li Dawei, Li Jiancheng, Jin Taoyong, et al. Accuracy Estimation of Recent Global Ocean Tide Models Using Tide Gauge Data[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 106-110)
(  0) 0) |
| [15] |
Matsumoto K, Takanezawa T, Ooe M. Ocean Tide Models Developed by Assimilating TOPEX/POSEIDON Altimeter Data into Hydro Dynamical Model:A Global Model and a Regional Model around Japan[J]. Journal of Oceanography, 2000, 56(5): 567-581 DOI:10.1023/A:1011157212596
(  0) 0) |
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Central South University, 932 South-Lushan Road, Changsha 410083, China
 2019, Vol. 39
2019, Vol. 39


