2. 武汉大学测绘学院,武汉市珞喻路129号,430079
随着智能手机的普及与无线通信技术的发展,室内定位需求日渐旺盛。在商场、大型停车场和商业综合体等复杂消费级定位场景,WiFi定位和行人航位推算(pedestrian dead reckoning,PDR)定位在精确度、穿透性、抗干扰性、布局复杂程度、投入成本和技术成熟度等方面综合表现优异[1]。WiFi定位信号覆盖范围广且技术成熟,但易受环境影响,定位坐标波动较大[2]。PDR定位基于设备集成传感器实现完全自主定位,不易受外界环境干扰,但无法确定初始位置且定位误差易累积[3]。WiFi定位与PDR定位可通过彼此间的优势互补,实现定位坐标融合,但由于PDR无法直接获取绝对初始位置,因此初始位置无法直接融合;另外,WiFi定位坐标波动较大,直接作为初始位置会降低后续融合定位的精度。
本文在研究WiFi定位和PDR定位实现方法的基础上,提出基于WiFi/PDR的初始位置融合解算方法。该方法以PDR中估算的相邻两步距离和航线角作为参照,计算前后两步WiFi定位坐标集合与参照标准的偏差,并通过距离和角度偏差阈值分别过滤偏差较大的结果,对于在阈值内的结果,按距离和角度综合偏离度选择最优定位坐标,实现高精度的初始位置解算。
1 基于WKNN的WiFi指纹定位法WiFi指纹定位将待定点位置指纹与已知位置的所有离线位置指纹通过遍历比较2种指纹间的信号相似度,参照相似度最高的位置估算待定点位置。常用的待定点位置估计方法包括确定性算法、概率性算法和人工神经网络算法[4]。其中确定性算法具有计算量小、存储量小等优势,适合在智能手机上使用。
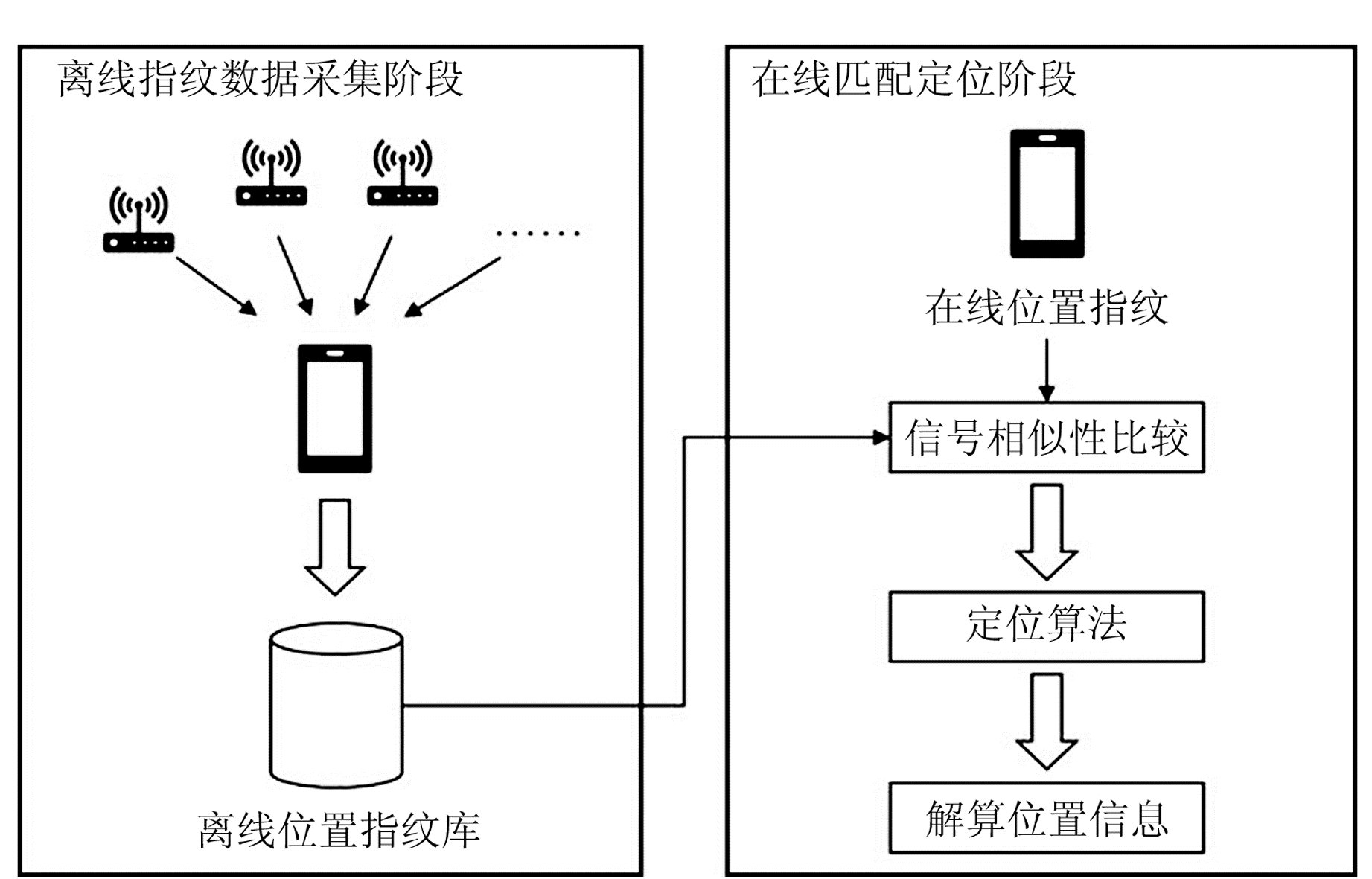
1.1 WiFi指纹定位原理在WiFi指纹定位中,由于接收信号强度(received signal strength,RSS)易获取且不受信号带宽影响,因此常被作为WiFi指纹定位的位置指纹。指纹定位分为离线指纹数据采集与在线匹配定位2个阶段[5],其定位原理如图 1所示。在第1阶段,基于已有区域地图划分采样点位置,全方位采集区域内离散位置的RSS,其中每个位置指纹中包含该位置所能接收的所有WiFi接入点(access point,AP)的RSS。为区分不同AP的RSS,同时记录AP的RSS和介质访问控制(media access control,MAC)地址,记为一条记录。一个位置下接收的所有AP记录构成一个位置指纹,区域内所有离散位置指纹即构成该区域的离线位置指纹数据库。在第2阶段,将待定点位置指纹与离线指纹数据库中的所有指纹进行遍历,比较相似度,选取相似度最高的前k个离线指纹取均值计算待定点位置。
|
图 1 WiFi位置指纹定位原理 Fig. 1 Principle of WiFi location fingerprint positioning |
作为确定性算法的典型代表,KNN算法基于与待定点相似度最高的k个已知位置的均值实现位置估计。为区分不同相似度指纹对定位坐标的不同影响,WKNN在KNN的基础上加入权值实现改进。由于不同智能手机在同一位置采集的RSS不一致,甚至存在较大差异,因此本文采用基于RSS余弦相似度的比较方法。
n维向量A和B的余弦相似度表示为:
| $ \begin{array}{*{20}{c}} {{\mathop{\rm sim}\nolimits} (\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{B}}) = \left[ {\sum\limits_{i = 1}^n {\left( {{A_i} \times {B_i}} \right)} } \right]/}\\ {\left[ {\sqrt {\sum\limits_{i = 1}^n {{{\left( {{A_i}} \right)}^2}} } \times \sqrt {\sum\limits_{i = 1}^n {{{\left( {{B_i}} \right)}^2}} } } \right]} \end{array} $ | (1) |
式中,Ai和Bi分别为向量A和B的某一维度分量。在sim(A, B)结果中,1表示完全相同,0表示完全独立,0~1之间的值表示相似度。
离线指纹表示为:
| $ {\rm{f}}{{\rm{p}}_i} = \left\{ {\left( {{M_1}, {R_{i1}}} \right), \left( {{M_2}, {R_{i2}}} \right), \cdots , \left( {{M_n}, {R_{in}}} \right)} \right\} $ | (2) |
在线指纹表示为:
| $ {{\rm{f}}{{{\rm{p}}_j}}} = \left\{ {\left( {{M_1}, {R_{j1}}} \right), \left( {{M_2}, {R_{j2}}} \right), \cdots , \left( {{M_n}, {R_{jn}}} \right)} \right\} $ | (3) |
式中,M为AP的MAC地址,R为对应AP的RSS,m和n分别为在线指纹fpj与离线指纹fpi的AP数量。
通过对fpi和fpj取交集的方式解决可能存在的维度缺失问题,fpi和fpj共有AP的MAC地址记为:
| $ {\rm{MA}}{{\rm{C}}_c} = \left\{ {{M_1}, {M_2}, \cdots , {M_k}} \right\} $ | (4) |
式中,k为共有AP总数。基于共有AP生成新的在线指纹和离线指纹:
| $ \begin{array}{*{20}{l}} {{\rm{f}}{{\rm{p}}_j}' = \left\{ {\left( {{M_1}, {R_{j1}}} \right), \left( {{M_2}, {R_{j2}}} \right), \cdots , \left( {{M_k}, {R_{jk}}} \right)} \right\}}\\ {{\rm{f}}{{\rm{p}}_i}' = \left\{ {\left( {{M_1}, {R_{i1}}} \right), \left( {{M_2}, {R_{i2}}} \right), \cdots , \left( {{M_k}, {R_{ik}}} \right)} \right\}} \end{array} $ | (5) |
将式(5)代入式(1),计算在线指纹与离线指纹的相似度,记为sim(fpi, fpj)。将sim值按大小排序,选择sim值最高的前k个离线指纹进行估算。
k个离线指纹中第a个参考点权重值记为:
| $ {w_a} = {{\mathop{\rm sim}\nolimits} _a}/\sum\limits_{b = 1}^k {{\rm{si}}{{\rm{m}}_b}} $ | (6) |
依据sim值对应的离线指纹坐标,按式(7)求得待定点位置:
| $ (\bar x, \bar y) = \sum\limits_{i = 1}^k {{w_a}} \left( {{x_a}, {y_a}} \right) $ | (7) |
PDR定位法是一种基于集成传感器完全自主式的惯性测量定位方法[6],本质上是一种利用相对位置关系定位的方法,其计算公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_k} = {x_0} + \sum\limits_{i = 1}^k {{l_i}} \sin {\theta _i}}\\ {{y_k} = {y_0} + \sum\limits_{i = 1}^k {{l_i}} \cos {\theta _i}} \end{array}} \right. $ | (8) |
式中,(x0, y0)和(xk, yk)分别为初始位置和当前位置,k为步数,l为步长,θ为航向角。
步数检测和步长估算是决定步数和步长的重要环节。对于步数检测,针对实际行走过程中智能手机位置随机、姿态随机引起的单轴加速度无法有效检测步数的问题,采用三轴线性综合加速度ac作为检测源数据。其中,
| $ {a_c} = \sqrt {a_x^2 + a_y^2 + a_z^2} $ | (9) |
一般采用峰值法计算步数[7]。针对综合线性加速度数据不规则变动引起的加速度曲线波峰数远超实际步数的问题,提出基于平均阈值的步数检测方法。在对综合线性加速度曲线移动平滑的基础上,以3 s为周期计算当前时间范围内的所有波峰的平均阈值PT:
| $ {\rm{PT}} = {\rm{PV}}/{\rm{PN}} $ | (10) |
式中,PV为3 s内所有波峰对应加速度值的和,PN为3 s内所有波峰数量。
平均阈值法可实现对无效波峰的有效筛选,结合人体0.2 s/步的极限行走速度,可实现更加精准的步数检测。已筛选波峰前后时间间隔至少为0.2 s,而对于一般定位情况,时间间隔可以放宽至0.4 s。将上述方法应用于实际实验中,在手持手机和将手机置于口袋分别行走5步和6步的情况下,检测结果也分别为5步和6步,实验准确度高达100%。
常用的步长估算模型包括线性频率模型[8]和Weinberg Approach模型[9]。两步长估算模型估计公式分别为:
| $ l{\rm{ = }}a{\rm{ }}f + b $ | (11) |
| $ l = K\sqrt[4]{{{a_{\max }} - {a_{\min }}}} $ | (12) |
式中,l为步长,f为步频,a和b为常数,amax和amin为行走中最大和最小加速度值,K为比例参数,为一常数。
2种模型的平均误差分别为0.08 m和0.03 m,误差均在cm级,对定位精度的影响基本可忽略。但线性频率模型计算量远小于Weinberg Approach模型,因此,选择前者作为步长估算模型。
初始航向角可由磁力传感器获得,记为A0,但磁力传感器易受室内环境影响。对此,提出磁力传感器+陀螺仪的航向角获取方法。该方法由磁力传感器获取初始方位,陀螺仪获取角度变化量。由于手机姿态未知,需将基于手机坐标系的陀螺仪角度变化转换成基于行人坐标系的Z轴角度变化。
研究发现,行人在行人坐标系的Z轴方向上受到恒定的加速度g,而手机坐标系中三轴的重力加速度和也为g,且三轴重力加速度方向与三轴陀螺仪方向一致,因此,提出基于重力加速度的坐标转换方法。转换过程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _{{Z_X}}} = \frac{{{g_x}\theta }}{{\sqrt {g_x^2 + g_y^2 + g_z^2} }} = \frac{{{g_x}{\theta _x}}}{g}}\\ {{\theta _Z} = {\theta _{{Z_X}}} + {\theta _{{Z_Y}}} + {\theta _{{Z_Z}}}} \end{array}} \right. $ | (13) |
式中,gx、gy、gz分别为手机坐标的三轴重力加速度,g为重力加速度,θx为手机坐标系x轴上陀螺仪角度变化量,θZ为行人坐标系Z轴的角度变化量。
航向角A可表示为:
| $ A = {A_0} + \sum\limits_{i = 1}^k {{\theta _{{Z_i}}}} $ | (14) |
精准的初始位置是融合定位精度的保证,而WiFi定位坐标存在一定的波动性,且PDR定位无法自行输出绝对初始位置。因此,提出基于WiFi/PDR的初始位置融合解算方法。
以频率f采集位置指纹,并依据平均阈值法检测的步数及对应的时间,提取出第i步采集的指纹信息,记为fpi。单次WiFi指纹可能不可靠,因此,继续提取第i步后的t时间内的指纹。行走1步共提取n个指纹:
| $ n = 1 + ft $ | (15) |
依据式(7)计算n个指纹的对应坐标,该坐标即为候选点位置,记为Si:
| $ {S_i} = \left\{ {\left( {{x_{i1}}, {y_{i1}}} \right), \left( {{x_{i2}}, {y_{i2}}} \right), \cdots , \left( {{x_{in}}, {y_{in}}} \right)} \right\} $ | (16) |
将Si-1中n个点与Si中n个候选点分别进行距离和方位计算,以评估已有轨迹行走到当前WiFi定位点的可能性。将Si-1中第m个点到Si中第j个参考点之间的距离记为lmj,连接线形成的向量与磁北极的夹角记为Amj,顺时针方向记为正方向,范围为(-180°,180°]。lmj和Amj具体可由式(17)求得:
| $ \begin{array}{l} \\ \left\{ \begin{array}{l} {l_{mj}} = \sqrt {{{\left( {{x_{ij}} - {x_{(i - 1)m}}} \right)}^2} + {{\left( {{y_{ij}} - {y_{(i - 1)m}}} \right)}^2}} \\ {A_{mj}}{\rm{ = }}\left\{ \begin{array}{l} \arctan \left( {\frac{{{y_{ij}} - {y_{(i - 1)m}}}}{{{x_{ij}} - {x_{(i - 1)m}}}}} \right), {x_{ij}} - {x_{(i - 1)m}} \ne 0\\ 0, {x_{ij}} - {x_{(i - 1)m}} = 0, {y_{ij}} - {y_{(i - 1)m}} > 0\\ \pi , {x_{ij}} - {x_{(i - 1)m}} = 0, {y_{ij}} - {y_{(i - 1)m}} < 0 \end{array} \right. \end{array} \right. \end{array} $ | (17) |
距离偏差值记为Δl:
| $ \Delta l = {l_{mj}} - l $ | (18) |
其中,l由式(11)求得。
角度偏差值记为ΔA:
| $ \Delta A = {A_{mj}} - A $ | (19) |
其中,A由式(14)求得。
由文献[10]可知,Δl和ΔA近似服从高斯分布,因此,假设Δl和ΔA服从高斯分布,可得:
| $ \left\{ \begin{array}{l} {p_l} = \frac{{{{\rm{e}}^{ - \frac{{\Delta l}}{{2\sigma _l^2}}}}}}{{\sqrt {2\pi } {\sigma _l}}}\\ {p_A} = \frac{{{{\rm{e}}^{ - \frac{{\Delta A}}{{2\sigma _A^2}}}}}}{{\sqrt {2\pi } {\sigma _A}}} \end{array} \right. $ | (20) |
式中,σl和σA分别为距离偏差和角度偏差的标准差,pl和pA分别为距离偏差和角度偏差的高斯概率分布。
对Δl和ΔA分别设定阈值,去除阈值外的所有点,实现备选结果的初步筛选,减小后期计算量。通过阈值限定,Si-1中任一点与Si中定位坐标的限定范围如图 2所示,每步只保留阴影区域内的WiFi定位坐标。

|
图 2 定位坐标限定范围 Fig. 2 Limited scope of positioning coordinates |
由于PDR定位中第1步与第0步的时间间隔无法界定,因此,从第2步开始进行初始化,计算所有符合条件的WiFi定位坐标的pl和pA,并按式(21)计算综合概率pU。
| $ {p_U} = {p_l}{p_A} $ | (21) |
对所有的pU进行排序,pU值最大的WiFi定位坐标作为下一步的初始位置,将第i步当前朝向与磁北极的夹角记为Ai,则第i+1步与第i步间的转角可记为:
| $ \Delta A = {A_{i + 1}} - {A_i} $ | (22) |
由于人在连续行走时相邻两步间的转角不会超过一定范围,即ΔA位于一定范围内,超过该范围,大概率上是定位发生偏差,此处即认为定位发生错误,定位结果重置,重新开始定位。结合定位的路径信息,通过ΔA的约束可进一步提高初始位置解算方法的稳定性,实现自我纠错,保证输出高精度的结果。通过连续几步定位,可使得定位误差逐渐降低收敛,并将概率最高的轨迹中最后的一个结点作为初始位置输出。
3.2 实验及分析分别选择红米Note 3和魅族MX 4 Pro作为离线指纹采集设备和在线指纹采集设备。定位过程中,WiFi数据采集频率为20 Hz,惯性传感器数据采集频率为50 Hz。
实验区域保持无人的理想定位状态下,在区域不同位置进行20次实验,每次实验分别计算WiFi定位误差及融合定位误差,误差均记为σ,实验结果如图 3所示。经计算,20次实验中,WiFi定位方法的中误差为3.0 m,而融合解算方法的中误差为1.2 m,实验误差缩小超50%。由图 3可看出,WiFi定位误差时大时小,表现不稳定。按不同误差区间统计2种方法误差分布比重,结果如表 1所示。可以看出,融合解算方法估算误差2 m以下的比重达到100%,而WiFi定位方法仅有40%,且WiFi定位方法中甚至有超过6 m的误差。

|
图 3 理想定位场景下WiFi定位方法与融合解算方法估算误差 Fig. 3 Estimation errors of WiFi location and fusion solution in ideal location scene |
|
|
表 1 理想定位场景下不同定位方法误差分布 Tab. 1 Error distribution of different locating methods in ideal location scene |
顾及行人因素,重述上述实验,以模拟实际复杂定位场景,相应计算结果见表 2。
|
|
表 2 复杂定位场景下不同定位方法误差分布 Tab. 2 Error distribution of different locating methods in complex location scene |
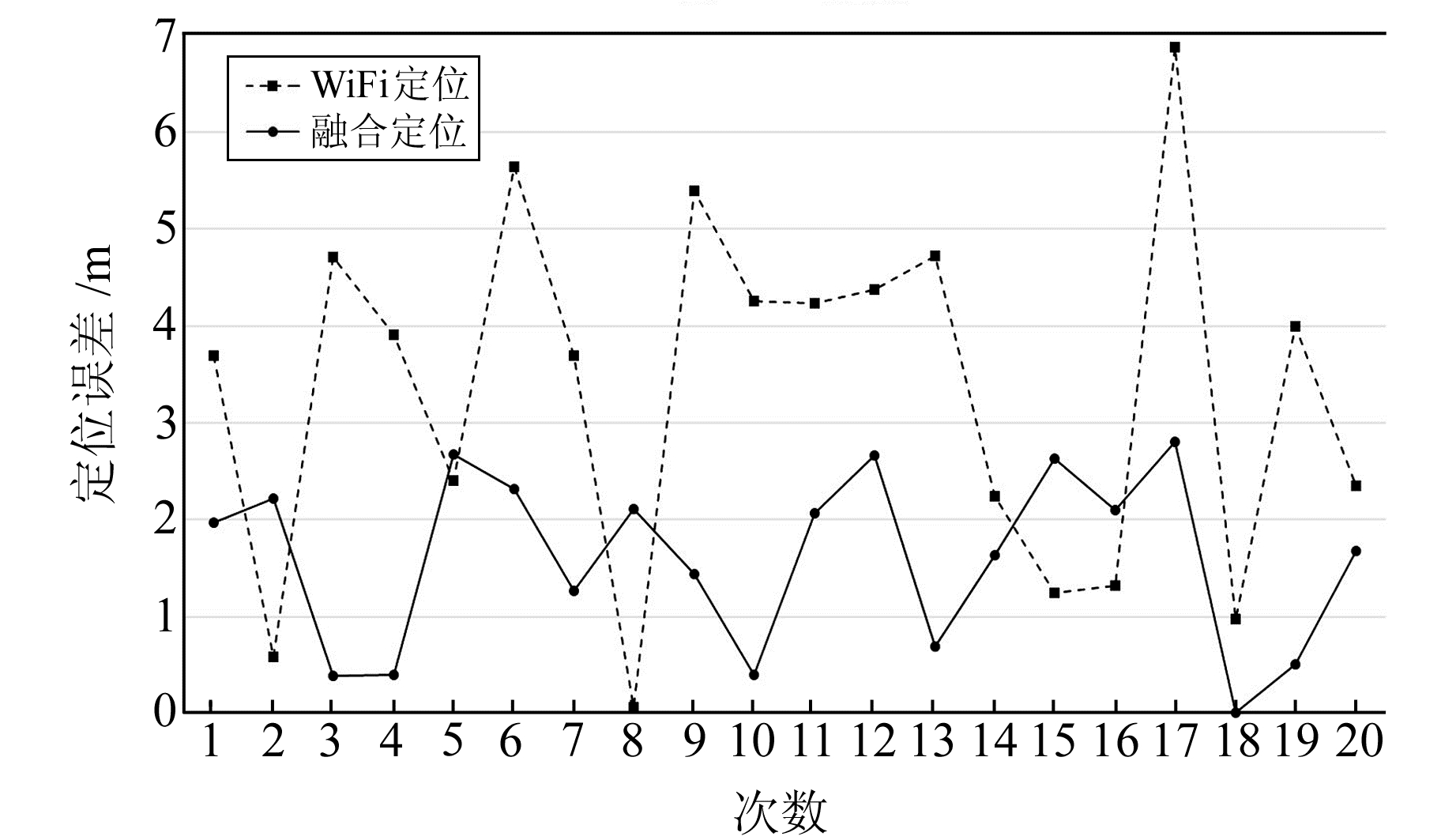
经计算,20次实验中WiFi定位方法的中误差为3.8 m,而融合解算方法的中误差为1.8 m,误差降低50%左右。相比理想定位场景,2种方法的精度均降低,WiFi定位方法中大于4 m的误差比重由15%增加至50%,融合解算方法中2~4 m的误差则由0增加至45%。但即使如此,融合解算方法表现仍旧稳定,所有点误差均小于3 m。
在图 3中,WiFi定位在第3、4、10、12、13、15、18和20次实验中均达到2 m以内的精度;在图 4中,WiFi定位在第2、5、8、14、15、16、18和20次实验中均达到3 m以内的精度。由此可见,WiFi定位可以实现较高的定位精度。但是,WiFi定位精度波动较大,融合解算方法则通过PDR方法中的角度和距离约束在一定程度上剔除了精度较差的定位结果,减小了WiFi定位结果的波动,提高了WiFi定位的整体精度。
|
图 4 复杂定位场景下WiFi定位方法与融合解算方法估算误差 Fig. 4 Estimation errors of WiFi location and fusion algorithm in complex location scene |
1) 针对WiFi指纹定位中设备差异性问题,采用余弦相似度比较信号相似度,并以此为权值实现WKNN定位算法。
2) 针对任意姿态下智能手机的PDR步数检测和航向角估计问题,分别提出基于综合线性加速度的平均阈值步数检测法和基于重力加速度的坐标转换法,以3 s为周期计算时间段内波峰对应综合线性加速度值的均值,并以此为阈值过滤无效波峰,结合相邻两步间的最小时间间隔,实现精准步数检测;基于陀螺仪数据,以重力加速度为纽带,实现手机任意姿态下手机坐标系到行人坐标系的转换,为航向角计算奠定基础。
3) 针对融合定位中初始位置不精准的问题,在研究WiFi定位、PDR定位实现方法的基础上,提出基于WiFi/PDR的初始位置融合解算方法。该方法定位精度为1.2~1.8 m,相比WiFi指纹定位误差缩小50%左右,且波动稳定,误差均小于3 m,为提供更准确、有效的室内定位服务奠定了基础。
| [1] |
姚碧超.室内WiFi定位技术研究[D].成都: 电子科技大学, 2017 (Yao Bichao. Research on Indoor Location Technology Based on WiFi[D]. Chengdu: University of Electronic Science and Technology, 2017) http://cdmd.cnki.com.cn/Article/CDMD-10614-1017077591.htm
(  0) 0) |
| [2] |
周飞.室内WiFi定位的研究[D].成都: 西南财经大学, 2016 (Zhou Fei. Study on Indoor WiFi Localization[D]. Chengdu: Southwest University of Finance and Economics, 2016)) http://cdmd.cnki.com.cn/Article/CDMD-10651-1017016717.htm
(  0) 0) |
| [3] |
黄承恺.多传感器信息融合算法在室内定位中的应用[D].北京: 北京邮电大学, 2015 (Huang Chengkai. The Application of Multi-Sensor Information Fusion Algorithm for Indoor Positioning System[D]. Beijing: Beijing University of Posts and Telecommunications, 2015)
(  0) 0) |
| [4] |
李冬, 张宝贤. 基于指纹的室内定位技术[J]. 中兴通讯技术, 2015, 21(6): 31-34 (Li Dong, Zhang Baoxian. Techniques for Fingerprint Based Indoor Localization[J]. ZTE Technology Journal, 2015, 21(6): 31-34 DOI:10.3969/j.issn.1009-6868.2015.06.008)
(  0) 0) |
| [5] |
殷虎. WLAN位置指纹室内定位技术[D].长沙: 湖南大学, 2016 (Yin Hu. An Indoor Localization Method Based on Location Fingerprinting in WLAN[D]. Changsha: Hunan University, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10532-1016252375.htm
(  0) 0) |
| [6] |
王珊.基于惯性传感器和WiFi联合室内定位方法的研究与实现[D].南京: 南京邮电大学, 2015 (Wang Shan. The Study and Implementation of Indoor Positioning Based on Inertial Sensors and WiFi[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2015) http://d.wanfangdata.com.cn/Periodical/zxtxjs201506008
(  0) 0) |
| [7] |
Mladenov M, Mock M. A Step Counter Service for Java-Enabled Devices Using a Built-in Accelerometer[C]. The 1st International Workshop on Context-Aware Middleware and Services: Affiliated with the 4th International Conference on Communication System Software and Middleware, Dublin, 2009 http://dl.acm.org/citation.cfm?id=1554235
(  0) 0) |
| [8] |
Li F, Zhao C S, Ding G Z, et al. A Reliable and Accurate Indoor Localization Method Using Phone Inertial Sensors[C]. 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, 2012 https://www.researchgate.net/publication/262211952_A_Reliable_and_accurate_indoor_localization_method_using_phone_inertial_sensors
(  0) 0) |
| [9] |
Weinberg H. Using the ADXL202 in Pedometer and Personal Navigation Applications[J]. Analog Devices AN-602 Application Note, 2002, 2(2): 1-6
(  0) 0) |
| [10] |
Lee S, Chon Y, Cha H. Smartphone-Based Indoor Pedestrian Tracking Using Geo-Magnetic Observations[J]. Mobile Information Systems, 2013, 9(2): 123-137 DOI:10.1155/2013/295838
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2019, Vol. 39
2019, Vol. 39

