2. 江苏省地震局,南京市卫岗路3号,210014
地磁低点位移异常是地磁垂直分量极小值出现低点的时间超前或滞后、在同一区域内相差小于2 h且大区域之间有明显分界线的现象。丁鉴海等[1-2]研究全国范围内的低点位移空间分布特点及其与地震的相关性,发现地震常发生在低点位移分界线附近,发震时间也与其相关。冯志生等[3]认为,这一反相位现象可能与地下电流分布出现畸变有关,即在低点位移异常期间,在分界线下方存在变化磁场的感应电流集中通过。
本文根据毕奥萨伐尔定理构建模型,计算线电流、竖直面电流和环电流的感应磁场,然后根据实测大地电磁数据反演的电性结构建立电流模型。使用该模型对电流的形态及深度进行约束,正演计算该电流引起的磁场,并关注该磁场叠加在正常Z分量上之后的特点。
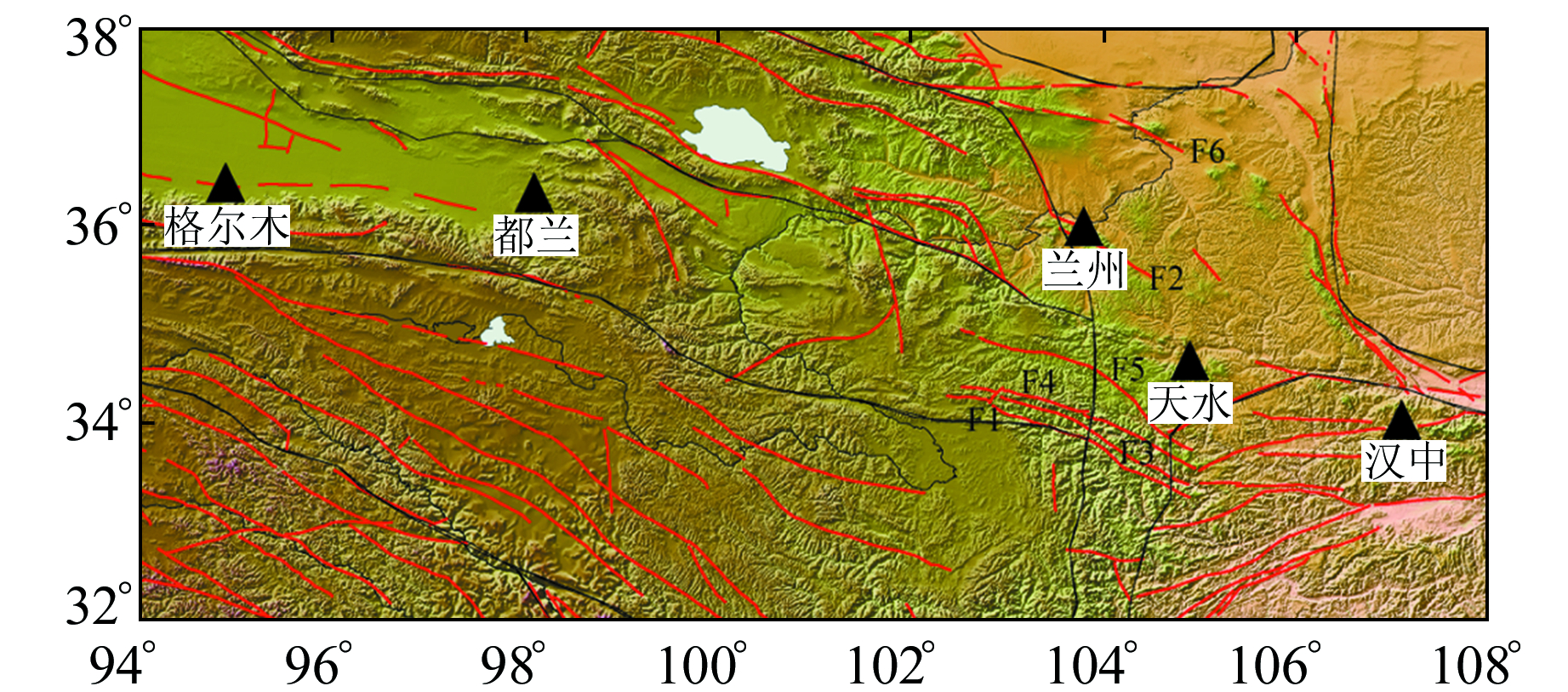
1 地磁观测背景和垂直分量反相位现象研究中使用的地磁场数据主要由2种观测仪器所获得:GM4磁通门仪(1 s采样),观测参量为水平分量H、磁偏角D、垂直分量Z;FHD质子磁力仪(60 s采样),观测参量为总场强度F、水平分量H、磁偏角D,单位均为nT。本文重点关注甘肃、陕西和青海省交界区域的地磁台站(图 1),拟使用2013年岷县漳县MS6.6地震前出现的低点位移异常数据,并综合现阶段对该区域电性结构的探测结果[4-5],建立正演计算Z分量反相位畸变的电流模型。
|
图 1 甘东南及邻区构造及台站分布 Fig. 1 Structure and station distribution of southeast Gansu and adjacent areas |
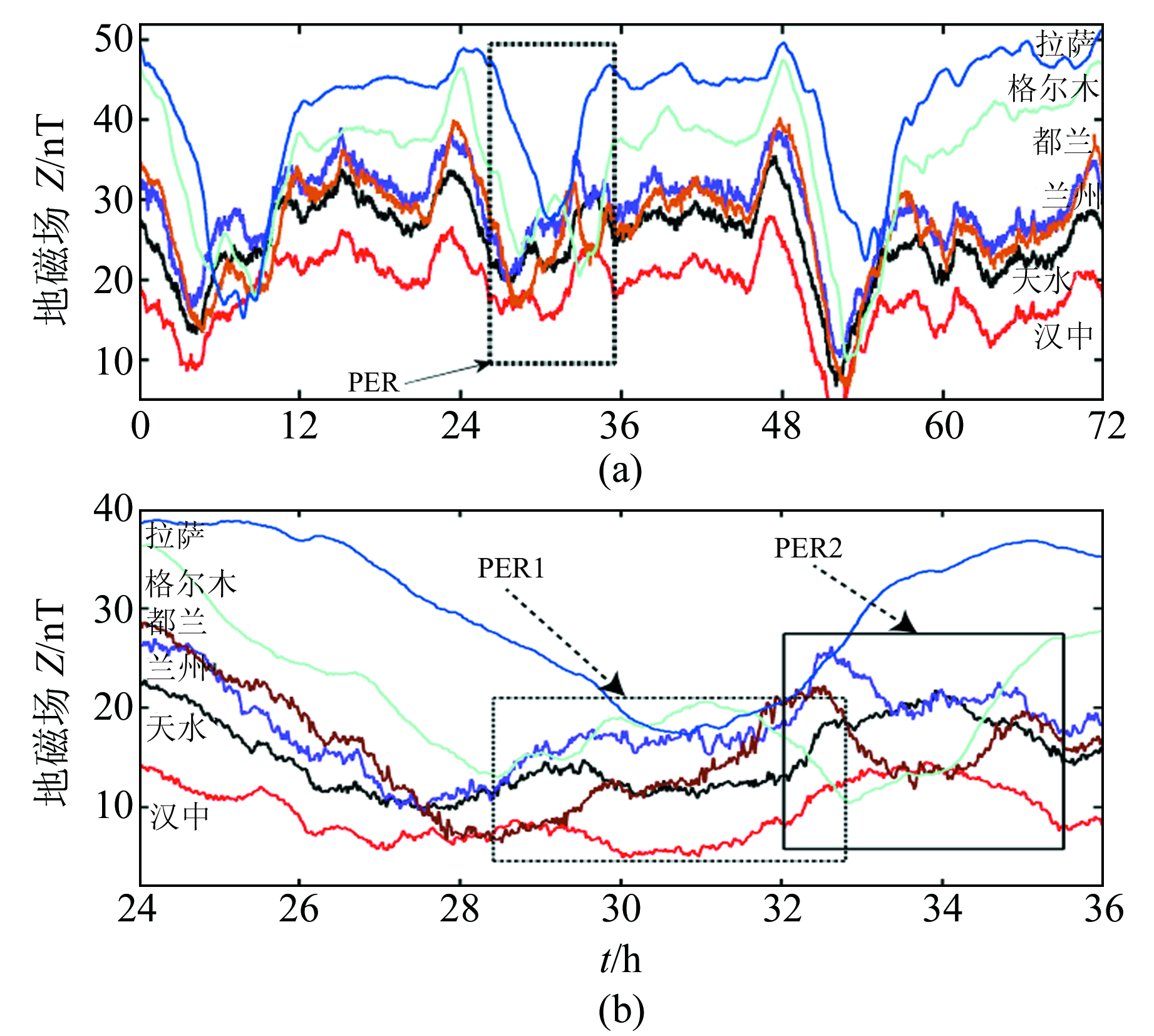
图 2为2013-06-16~06-18(UTC)汉中等6个台站的Z分量。可以看出,多个台站Z分量曲线在06-17 00:00后的低点出现异常。图 2(a)中PER框内,除拉萨外,其余5个台站的Z分量出现双低点的反相位现象。把PER部分放大在图 2(b)中,得出存在反相位的2个时段:在PER1的格尔木台和汉中台/天水台都存在相反的趋势;在PER2,都兰、兰州的曲线趋势与天水、汉中相反;格尔木台的相位与它们不一致,也可能在该时段内存在反相位现象。此外,所有反相位的幅度均小于11 nT,其中格尔木台最明显,约为10 nT,其余台站在5 nT左右。
|
图 2 地磁Z分量的反相位现象 Fig. 2 Anti-phase phenomenon of geomagnetic Z components |
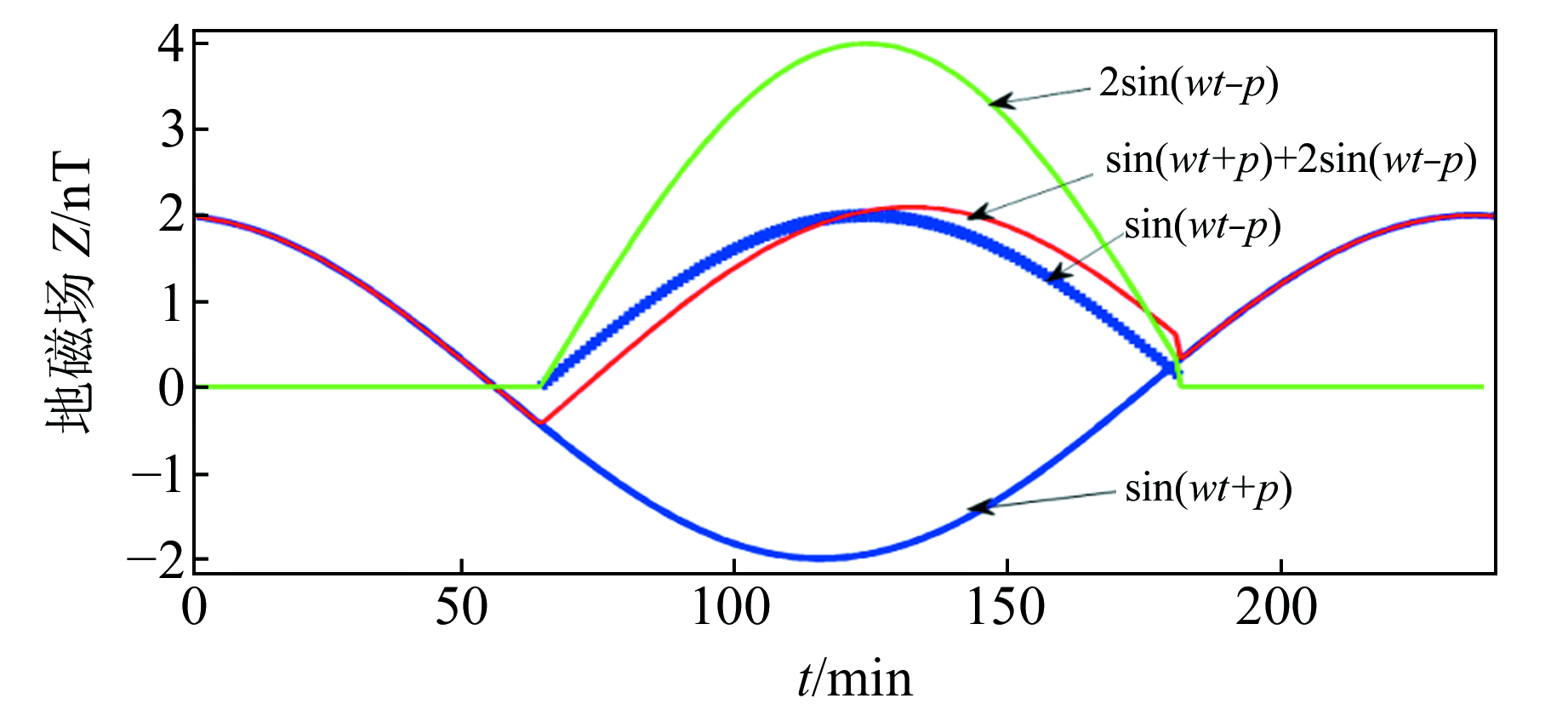
对于这种Z分量的反相位现象,大多数的解释与电流异常有关。图 3定量示意了其叠加现象,蓝线sin(ωt+p)为正常一个周期的曲线,蓝色粗线sin(ωt-p)为畸变电流产生的磁场,若它叠加在正常磁场曲线上,将会出现反相位效果(红线);若叠加在Z分量上,将导致低点时间超前或滞后,也会出现与其他未叠加或反向叠加的台站反相位的现象。另外,正向叠加使该畸变电流产生的磁场原始曲线的幅度增加,当畸变磁场与原始磁场存在较小的相位差时,也可能产生低点时间位移现象。
|
图 3 反相位现象的电流畸变效应 Fig. 3 Current distortion effect of anti- phase phenomenon |
稳定电流感应的磁场与电导率无关,因此可利用毕奥萨法尔定理计算感应磁场的强度。首先考虑简单的线电流分布,根据毕奥萨法尔定理以及对有限长线电流的积分结果:
| $ B = \frac{{{\mu _0}I}}{{4\pi a}}\left( {\cos {\theta _1} - \cos {\theta _2}} \right) $ | (1) |
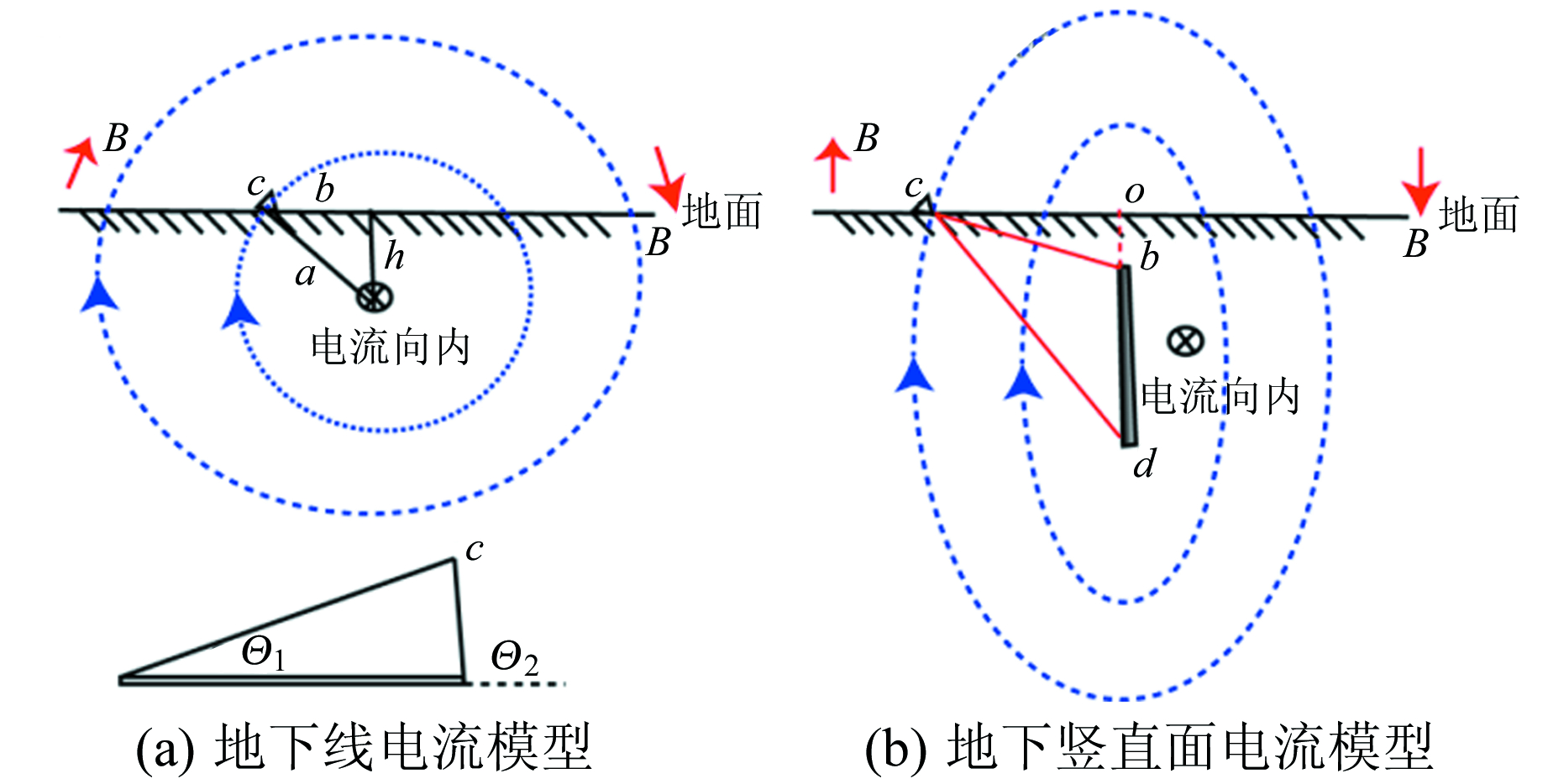
式中,θ1和θ2为直线外一点与线电流两端连线的偏角,a为电流线与测点的距离(图 4),真空中磁导率μ0=4π×10-7 N ·m/A,I为线电流的强度。式(1)说明,线外一点的感应磁场与电流强度和距离的倒数相关。实际应用中,相对于地面的一点,线电流可看成是无限长或半无限长,那么θ1和θ2分别为0和π或者π/2和π,则磁感应强度B变为
|
图 4 线电流和面电流模型 Fig. 4 Line current and surface current model |
| $ B = \frac{{{\mu _0}I}}{{4\pi \sqrt {{h^2} + {b^2}} }} $ | (2) |
竖直面电流只需按照线电流模型进行积分即可。如图 4(b),b为面电流顶深度,d为底深度,c为观测点距地面投影点o的距离,则:
| $ {B_{{\rm{s}}1}} = \frac{{{\mu _0}I}}{{2\pi (b - d)}}\ln \left( {\frac{{b - d + \sqrt {{b^2} + {c^2}} }}{{\sqrt {{b^2} + {c^2}} }}} \right) $ | (3) |
水平面电流则只需要将观测点旋转90°即可。在b-d的宽度范围,地磁场仅有水平分量,垂直分量为0,宽度为a,深度为h。考虑中心点上方朝一侧移动量b,则式(3)变为:
| $ {B_{s2}} = \frac{{{\mu _0}I}}{{2\pi a}}\ln \frac{{\sqrt {{{(b - a/2)}^2} + {h^2}} }}{{\sqrt {{{(b + a/2)}^2} + {h^2}} }} $ | (4) |
线电流的感应磁场如图 5。不同深度的电流感应磁场具有不同的衰减速度,电流越深或强度越大,感应场在空间上衰减越慢,两侧的畸变值差别越小。当电流强度随时间缓慢变化形态如正弦时,观测值也随时间有相同的变化,某些时刻的磁场出现极小值。图 5(a)将时间和距离变化显示在平面图上,自地面投影点向两侧的磁场方向相反,电流随时间变化时两侧磁场相位与电流变化一致。
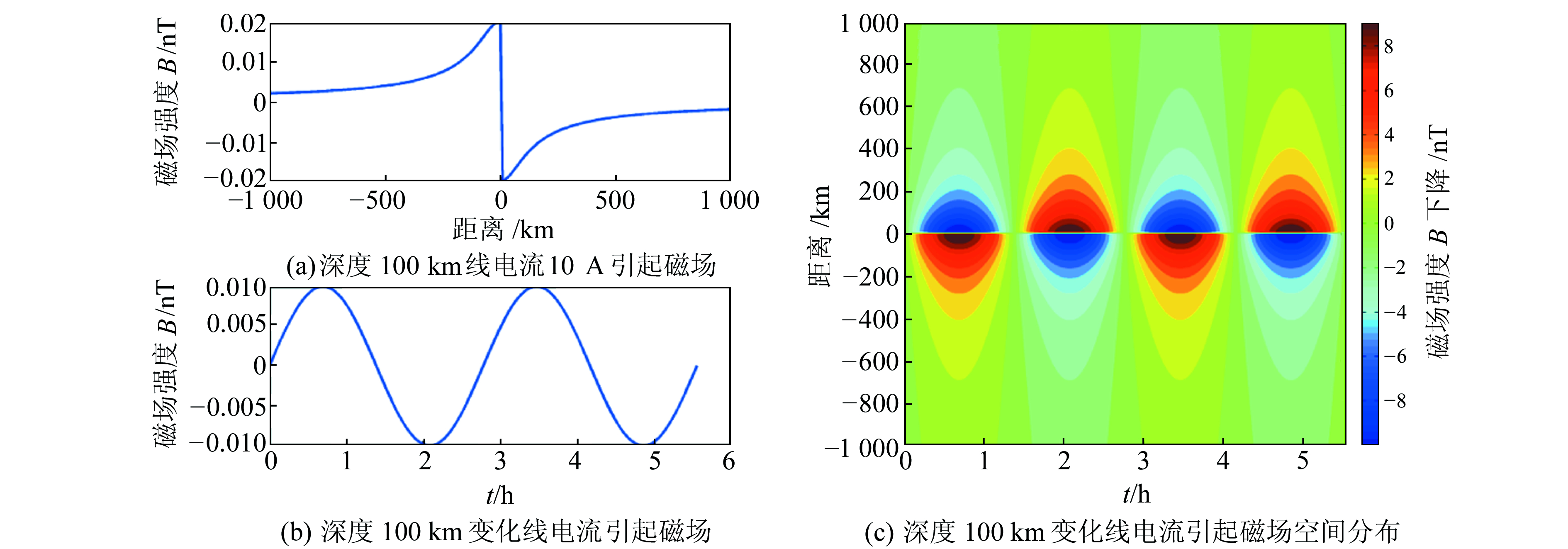
|
图 5 线电流的感应磁场分布 Fig. 5 The geomagnetic field induced by line current |
考虑面电流时,由于增加了深度,在两侧观测点延伸时感应场衰减较慢。如图 6(a),在100 km的深度上,磁感应强度在地面两侧变小的速率慢得多。此外,与线电流相比,当电流强度变化时(图 6(b)),磁感应强度也相应变化,投影点两侧对称分布,距离越远其强度越小(图 6(c)),变化特点与线电流模型类似。

|
图 6 竖直面电流的感应磁场 Fig. 6 The geomagnetic field induced by vertical surface current |
在实际应用中,电流的分布并非简单的线电流或面电流,而是更复杂的组合形态。下面考虑线电流和面电流的组合。假设有地下深100 km、宽10 km(+100 km)的竖直面电流,最大带电10 000 A,随时间变化满足函数sin(ωt)(图 7(b)红线),叠加地下深度50 km、最大50 A变化电流,满足sin(3ωt)(图 7(b)蓝线),结果如图 7。首先给出的面电流磁场向两侧衰减很慢,线电流衰减快,变化也快。叠加效果如图 7(b),在长周期的面电流感应磁场上叠加了短周期变化的线电流磁场。它们在时空平面上叠加时(图 7(c)),既体现了长周期的面电流变化状态,也表现了短周期的线电流叠加效果,部分时段为相互叠加,部分时段又表现为相互抵消。
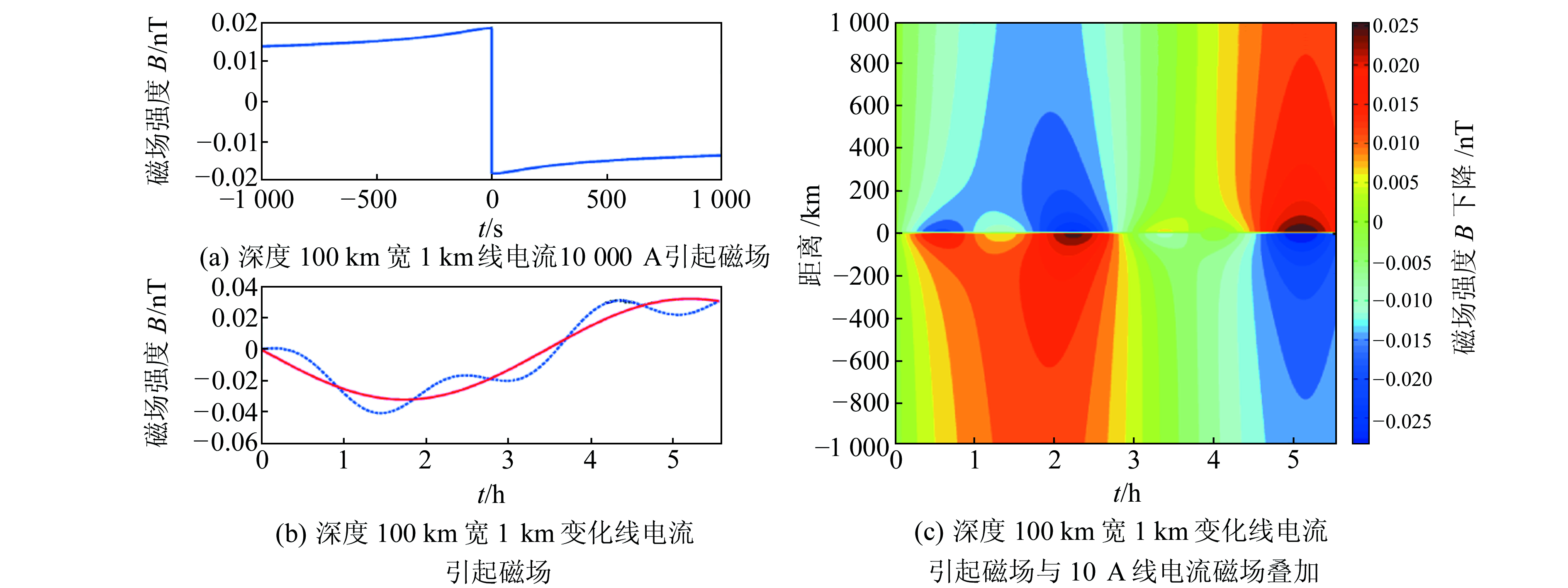
|
图 7 线电流和面电流叠加的感应磁场 Fig. 7 The geomagnetic field induced by line current and surface current superposition |
以岷县漳县地震区域为例,进行该区域的Z分量畸变的源电流模拟计算。首先基于前人在甘东南地区研究的大地电磁测深剖面,获取该区域电性结构信息。赵凌强等[5]认为西秦岭造山带下方存在不连续的高导区域,在临潭东北部高导区域深度顶部较浅,大约10 km,底部深度约为30~40 km,电导率随深度加深逐步变高,宽度在20 km左右。从赵凌强等[5]给出的另一条剖面来看,岷县和陇西之间还存在一个高导区域,顶部深度约为10 km,其分布处于F5下方(图 1、图 8(a)),可能为岷县下方高导区的延伸,宽度在10 km左右。此外,在岷县下方的高导区域分布较深,位于F5下方,顶部深度约20 km,朝NE向倾斜,较深部分和浅部的电导率均高于中心区域。临洮西南部的F2下方以及陇西到岷县之间的F2下方同时分布2个高导区域,它们之间以F2的向下延伸为界线,深度在5~30 km之间,宽度在25 km左右。另外,在迭部县附近F4和F3之间的下方也存在约10 km的高导区域。詹艳等[4]的反演结果显示,在礼县和西和县下方存在大范围的高导区域,深度5~20 km,顶面宽度20 km,电阻率5~10 Ωm,可能为岷县下方高导区域的延伸。
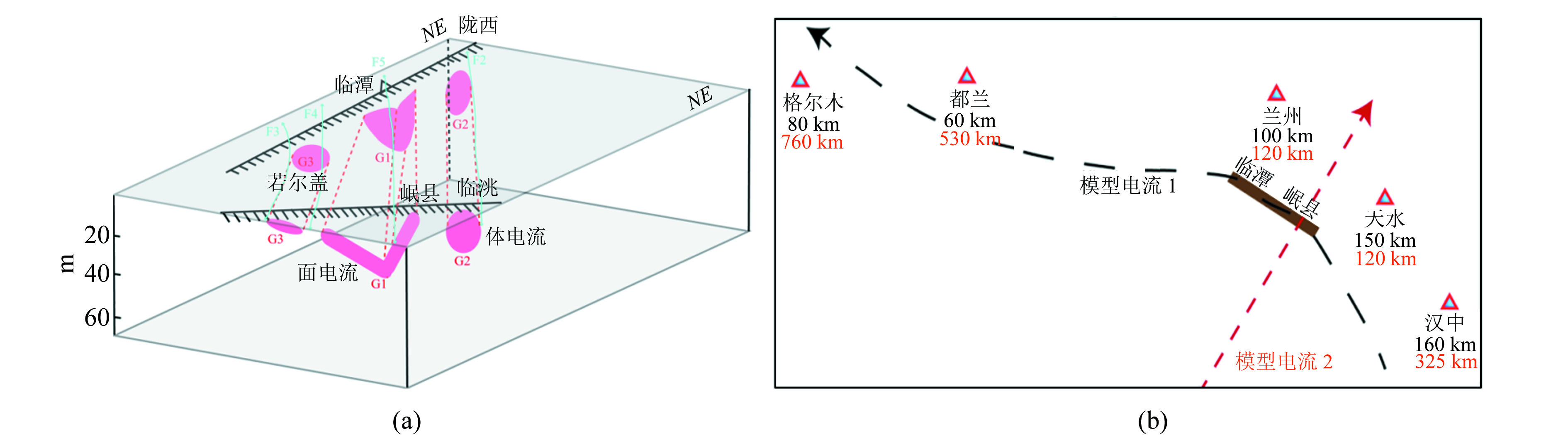
|
图 8 基于实际电性结构的电流模型(黑色数字为模型1距离,红色为模型2距离) Fig. 8 The current model based on actual electric structure |
由上述分析可知,在岷县漳县地震区域考虑3个区域的高导结构,其中G1为主要高导区域(图 8),是发震断层所在,也是畸变电流最可能出现的区域[4-5]。其在F5下方,即地震的发震断层附近NE向倾斜,深度10~30 km,向西可能延伸到临潭附近,向东可能延伸到西和县附近,电阻率两头低中间高,约为8~40 Ωm,宽度10 km左右。G2在F2下方西侧,圆柱状延伸至临洮西侧,电阻率变高、范围变宽,有向下倾斜趋势,深度10~40 km,电阻率5~50 Ωm,宽度20 km左右。G3在F4和F3之间下方/迭部县东北侧,向西倾斜,深度5 km左右,电阻率10~80 Ωm,顶面宽度约40 km。
图 8中,在岷县下方(F5下侧)存在倾斜的面电流,“V”字形的两侧面电流相叠加。面电流的倾斜相当于地面发生同样角度的倾斜,若倾斜角为θ,则感应磁场结果为Bs/cosθ。在大多数介质中,μ/μ0接近于1,即磁导率近似为μ0,对某一点处的电流感应磁场计算结果并无影响。当考虑离电流投影在地面区域较远一点时,其感应磁场与面电流中心线的距离有关,与面电流的倾斜程度无关,因此使用式(4)计算电流感应磁场Bs2。图 9(a)是地下5 km处倾斜30°的面电流在地表的感应磁场Bs2,与竖直面电流的感应场相比,感应场朝两侧衰减更慢、中间段更平缓。同时,靠近面电流在地面投影处,磁场在垂直方向的分量较小。

|
图 9 倾斜面电流的感应磁场空间分布 Fig. 9 The spatial distribution of geomagnetic field induced by the tilting current |
图 9(b)是基于图 8(a)模型计算出的感应磁场在地面的分布情况,倾斜面电流的磁场在分界线附近并不立即反向,其缓慢过渡的趋势可能更符合实际,最大感应磁场幅度不是出现在分界线附近,出现点与面电流的宽度有关。感应场向两侧的衰减趋势平缓,即处于离电流投影位置远近不同的台站,其观测到的感应磁场幅度差异不是很大。
表 1给出图 8(b)中2个电流模型的感应磁场计算结果,其中模型1的电流强度为5 000 A,模型2的电流强度为10 500 A,深度都为5 km,2个模型的实测幅度分别对应于图 1中的PER1和PER2时段。对于模型1(图 8(b)中黑色数字)的结果,由于格尔木和都兰台附近的电性结构并不清楚,这个结果仅作为两者实测值的参考,说明可通过电流模型达到反相位叠加的效果。模型2(图 8(b)中红色数字)是在甘东南地区电性结构比较清楚的情况下建立的,可能更接近于实际电流的空间位置和形状。但模型2也有其适用范围,如兰州和天水台的感应磁场强度都比较接近于实测幅度,较远的都兰和格尔木台差异比较大。
|
|
表 1 在不同台站处的实测及电流模型感应磁场 Tab. 1 Measured values and induced values at different stations |
现阶段对于低点位移的形成机制都趋向于电流异常的解释。张学民等[6]对低点位移作频谱分析后认为,低点位移异常的产生与天地电磁层-岩石圈的电磁耦合效应相关,并且根据趋肤深度效应推断可能与岩石圈下部或深部地幔物质上涌或横向迁移有关。潘晖等[7]基于对地震前电流涡出现纬向偏移现象,将低点位移解释为逆时针电流感应磁场的叠加。袁桂平等[8]通过分析汶川地震前后的Sq等效电流发现,在地磁Z低点位移发生时,内源等效电流体系电流涡中心电流下降较大,说明低点位移现象与内源电流的关系密切。以上论述在一定程度上满足产生低点位移的条件,但未反映出低点位移时不同台站之间的反相位现象。冯志生等[3]基于低点位移时台站之间的反相位现象,提出地下电流畸变的成因模型。该模型能够解释在低点位移线两侧出现的反相位现象,也能对电流感应磁场的叠加效应给出可靠的理论依据。电流感应磁场的叠加效应在不同时间段会出现不同的曲线畸变,在一定程度上解释了多种低点位移发生时的曲线畸变,说明这一模型是相对完善的。
在计算电流感应磁场的过程中,畸变电流的变化非常缓慢,近似于稳恒电流,因此直接使用毕奥萨伐尔定理计算该电流的感应磁场。对于这种计算方法的适用性:1)此处讨论的仅仅是引起低点位移缓慢变化的电流,其缓慢程度与低点位移变化的程度相当,即约2 h内变化幅度小于1 nT。尽管图 4~7给出了类似于正弦变化的电流形式,大致以几个小时为周期,相应的变化电流对于交变电流来说仍可看作是缓慢变化的。2)如果电流场附近存在磁介质,在磁介质中会有磁化电流产生,此时计算电流的感应磁场可选用电镜像法或是需要求解满足特殊边界条件的拉普拉斯方程的磁标势法,但这2种情况在本文的前提假设中无必要,本文目的是能够通过求取一定形式的电流来满足低点位移的变化情形,从而为低点位移反演畸变电流提供帮助。
本文中模型1综合电性结构给出了可能的电流深度,模型2根据图 1中断裂带的走向给出了畸变电流的可能空间范围。在地下电流畸变模型框架内,定量给出不同深度和强度、空间形状的畸变电流模型产生的磁场,测试它们的叠加效果。文中还考虑了实际的电性结构,以及是否有利于畸变电流的产生,从而叠加在实际观测曲线上。但基于大地电磁反演结果一般只能给出较浅部的电性结构,对于到达岩石圈底部甚至上地幔的电流分布,更多地只能通过长周期地磁测深给出。另外,还必须考虑电流通道效应[9-10],若出现比较复杂的电流形态,必然存在相应的电流通道,即实际电性结构有利于电流的形成或触发畸变电流。单一电流的形成,并不能产生比较复杂的低点位移及其反相位现象,可能其中某电流具有触发效应,触发了与其相关的一系列畸变电流的出现。
文中计算的2个模型也不能完全拟合叠加畸变的曲线部分,因此有必要考虑主要电流的形成对周边一些具备形成电流的介质造成触发,导致在主电流附近形成一系列分支电流,这些分支电流的分布依照既有的电流通道,致使其感应磁场成为更复杂的形态。对于模型1,都兰台在某个时段与兰州台的相位一致,则可以推测两者处于电流的同侧;如果电流分布处于都兰台与格尔木台之间,则解释了两者的反相位关系。在观测中发现的地磁垂直分量Z低点位移异常伴随反相位现象,依据正演计算结果,可以较完善地解释这种现象。如果能在低点位移发生后及时计算出电流异常的位置和强度,分析低点位移的成因机制,对于判断地震地磁异常的效能应有帮助。
| [1] |
丁鉴海, 卢振业, 黄雪香. 地震地磁学[M]. 北京: 地震出版社, 1994 (Ding Jianhai, Lu Zhenye, Huang Xuexiang. Seismic Geomagnetism[M]. Beijing: Seismological Press, 1994)
(  0) 0) |
| [2] |
丁鉴海, 刘杰, 余素荣, 等. 地磁日变化异常与强震的关系[J]. 地震学报, 2004, 26(增1): 79-87 (Ding Jianhai, Liu Jie, Yu Surong, et al. Geomagnetic Diurnal-Variation Anomalies and Their Relation to Strong Earthquakes[J]. Acta Seismologica Sinica, 2004, 26(S1): 79-87)
(  0) 0) |
| [3] |
冯志生, 李琪, 李鸿宇, 等. 地磁低点位移线两侧异常变化的反相位现象及其解释[J]. 中国地震, 2009, 25(2): 206-213 (Feng Zhisheng, Li Qi, Li Hongyu, et al. Anti-Phase Phenomena on Two Sides of Geomagnetic Low-Point Displacement Line and Its Interpretation[J]. Earthquake Research in China, 2009, 25(2): 206-213 DOI:10.3969/j.issn.1001-4683.2009.02.012)
(  0) 0) |
| [4] |
詹艳, 赵国泽, 王立凤, 等. 西秦岭与南北地震构造带交汇区深部电性结构特征[J]. 地球物理学报, 2014, 57(8): 2594-2607 (Zhan Yan, Zhao Guoze, Wang Lifeng, et al. Deep Electric Structure beneath the Intersection Area of West Qinling Orogenic Zone with North-South Seismic Zone in China[J]. Chinese Journal of Geophysics, 2014, 57(8): 2594-2607)
(  0) 0) |
| [5] |
赵凌强, 詹艳, 陈小斌, 等. 西秦岭造山带(中段)及其两侧地块深部电性结构特征[J]. 地球物理学报, 2015, 58(7): 2460-2472 (Zhao Lingqiang, Zhan Yan, Chen Xiaobin, et al. Deep Electrical Structure of the Central West Qinling Orogenic Belt and Blocks on Its Either Side[J]. Chinese Journal of Geophysics, 2015, 58(7): 2460-2472)
(  0) 0) |
| [6] |
张学民, 钱家栋, 王亚丽, 等. 地磁低点位移频谱特征及机理探讨[J]. 地震学报, 2008, 30(5): 474-483 (Zhang Xuemin, Qian Jiadong, Wang Yali, et al. Spectral Features of Geomagnetic Low Point Displacement and Discussion on Its Mechanism[J]. Acta Seismologica Sinica, 2008, 30(5): 474-483 DOI:10.3321/j.issn:0253-3782.2008.05.005)
(  0) 0) |
| [7] |
潘晖, 张建国, 杨冬梅, 等. 地震地磁低点位移成因的一种可能机制[J]. 大地测量与地球动力学, 2014, 34(4): 83-87 (Pan Hui, Zhang Jianguo, Yang Dongmei, et al. A Possible Mechanism of the Contributing Factor of Geomagnetic Lowest Shift[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 83-87)
(  0) 0) |
| [8] |
袁桂平, 张学民, 吴迎燕, 等. 汶川8.0级地震前地磁低点位移与内外源Sq等效电流体系关系的研究[J]. 地震, 2015, 35(3): 102-112 (Yuan Guiping, Zhang Xuemin, Wu Yingyan, et al. Minimum Point Shift of the Geomagnetic Vertical Component in Diurnal Variation and the Internal-External Equivalent Current System Sq before the 2008 Wenchuan MS8.0 Earthquake[J]. Earthquake, 2015, 35(3): 102-112 DOI:10.3969/j.issn.1000-3274.2015.03.011)
(  0) 0) |
| [9] |
范国华, 姚同起, 顾左文, 等. 琼州海峡地区地磁变化特征及其分析[J]. 地震学报, 1994, 16(2): 220-226 (Fan Guohua, Yao Tongqi, Gu Zuowen, et al. Characteristics and Analysis of Geomagnetic Changes in the Qiongzhou Strait Region[J]. Acta Seismologica Sinica, 1994, 16(2): 220-226)
(  0) 0) |
| [10] |
Sarlis N, Lazaridou M, Kapiris P, et al. Numerical Model of the Selectivity Effect and the ΔV/L Criterion[J]. Geophysical Research Letters, 1999, 26(21): 3245-3248 DOI:10.1029/1998GL005265
(  0) 0) |
2. Jiangsu Earthquake Agency, 3 Weigang Road, Nanjing 210014, China
 2019, Vol. 39
2019, Vol. 39

