自Baarda提出粗差探测理论以来,学者们对粗差探测方法进行大量研究。於宗俦等[1]提出的多维粗差探测(LEGE)算法虽然能实现粗差的定值定位,但计算量较大; 施闯等[2]通过对改正数向量与观测量影响向量之间的相关系数进行假设检验来探测多个粗差; 陈玮娴等[3]将抗差估计与总体最小二乘法结合,使总体最小二乘法也具有抵抗粗差的能力; 王建民等[4]提出一种用方差比峰值作为粗差搜索结束标志的粗差探测方法; 刘陶胜等[5]通过分析极差与粗差判断区间的关系,用双极差判断矩阵探测粗差; 金丽宏等[6]根据均值漂移模型构建的检验统计量探测粗差。抗差估计在减弱粗差影响方面取得一定成效,但仍存在以下问题:一是如何选取合适的权函数,抗差的严密精度有待进一步研究[7]; 二是降权临界值的选取[8],且随着粗差数量的增加,抗差估计的性能逐步衰减[9]。本文通过改进传统的向后-向前法来定位粗差,同时根据推导出的粗差估值公式修正含有粗差的观测值,从而提高平差解算的精度和可靠性。
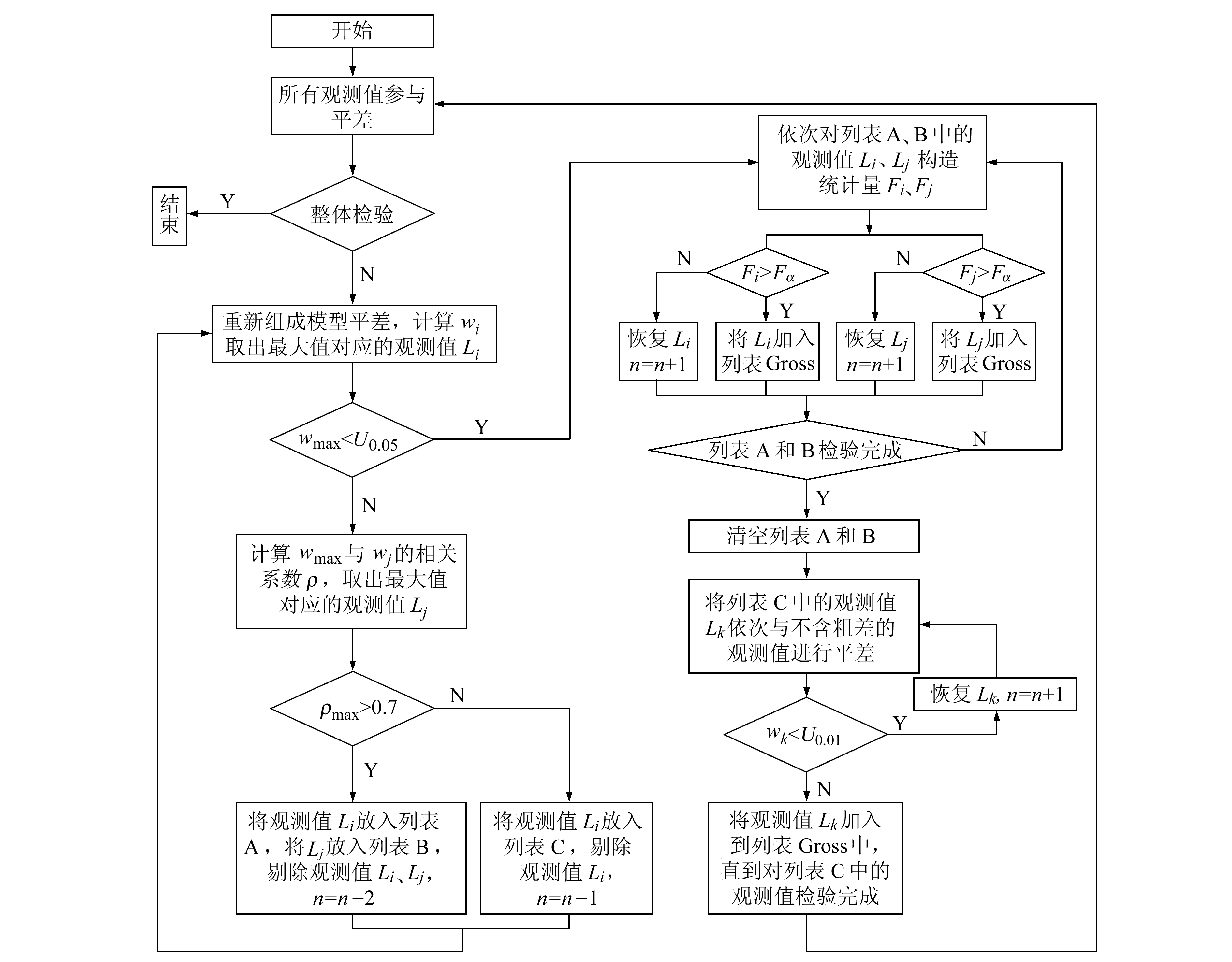
1 粗差定位的基本原理 1.1 传统的向后-向前选择法传统的向后-向前选择法BFS的粗差探测思路:在向后选择阶段,利用数据探测法筛选出怀疑含粗差的观测值; 在向前选择阶段,将粗差怀疑对象依次恢复到正常观测值中,对每一个怀疑对象单独检验,确定真正含有粗差的观测值。
1.2 改进的向后-向前选择法改进的向后-向前选择法IBFS(improved BFS)中,首先加入平差模型的整体检验; 其次,在向后选择过程中筛选粗差怀疑对象,同时找出与其统计量相关的观测值,并将这些观测值也视为粗差怀疑对象。最后,对统计量相关的观测值利用偏相关系数检验其是否含有粗差; 对于不具有统计量相关的观测值,则进入向前选择过程,进一步确定是否含有粗差。
1.2.1 平差模型的整体检验整体检验的基本思想为:先验单位权方差σ02与平差得到的后验方差
| $ {\chi ^2} = \frac{{{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}}}}{{\sigma _0^2}} \sim {\chi ^2}(f) $ | (1) |
式中,V为平差后得到的n×1阶残差向量,P为n×n阶观测值权阵,σ02为先验单位权方差,f为平差模型的自由度。当
若先验单位权中误差未知,可以按照等级确定。以水准网平差为例,若是二等水准测量,则σ0=1.0 mm; 若是三等水准测量,则σ0=3.0 mm。
1.2.2 Baarda数据探测法构造标准化残差统计量:
| $ {w_i} = \frac{{\left| {{v_i}} \right|}}{{{\sigma _0}\sqrt {{q_{{v_i}}}} }} \sim N(0,1) $ | (2) |
式中,σ0为先验单位权中误差,vi为第i个观测值的残差,qvi为残差协因数阵QVV主对角线上第i个元素的值。当
粗差定位转移即观测值Li含有粗差,却检测出观测值Lj含有粗差,可能是由于构建的统计量之间的相关性,使
| $ {w_i} = \frac{{\left| {{v_i}} \right|}}{{{\sigma _0}\sqrt {{q_{{v_i}}}} }} = \frac{{\mathit{\boldsymbol{e}}_i^{\rm{T}}\mathit{\boldsymbol{V}}}}{{{\sigma _0}\sqrt {{q_{{v_i}}}} }} $ | (3) |
| $ {w_j} = \frac{{\left| {{v_j}} \right|}}{{{\sigma _0}\sqrt {{q_{{v_j}}}} }} = \frac{{\mathit{\boldsymbol{e}}_j^{\rm{T}}\mathit{\boldsymbol{V}}}}{{{\sigma _0}\sqrt {{q_{{v_j}}}} }} $ | (4) |
式中,ei和ej分别表示第i和第j个元素为1、其余元素全为0的列向量。
根据协方差传播律,wi和wj的协方差为:
| $ \begin{array}{l} {\sigma _{{w_i}{w_j}}} = \frac{{\mathit{\boldsymbol{e}}_i^{\rm{T}}}}{{{\sigma _0}\sqrt {{q_{{v_i}}}} }}D\left( \mathit{\boldsymbol{V}} \right){\left( {\frac{{\mathit{\boldsymbol{e}}_j^{\rm{T}}}}{{{\sigma _0}\sqrt {{q_{{v_j}}}} }}} \right)^{\rm{T}}} = \\ \frac{{\mathit{\boldsymbol{e}}_i^{\rm{T}}}}{{{\sigma _0}\sqrt {{q_{{v_i}}}} }}\sigma _0^2{\mathit{\boldsymbol{Q}}_{VV}}\frac{{{\mathit{\boldsymbol{e}}_j}}}{{{\sigma _0}\sqrt {{q_{{v_j}}}} }} = \frac{{\mathit{\boldsymbol{e}}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_{VV}}{\mathit{\boldsymbol{e}}_j}}}{{\sqrt {{q_{{v_i}}}{q_{{v_j}}}} }} = \frac{{{q_{{v_{ij}}}}}}{{\sqrt {{q_{{v_i}}}{q_{{v_j}}}} }} \end{array} $ | (5) |
由于wi和wj都服从标准正态分布,所以有σwi=1,σwj=1。故统计量之间的相关系数为:
| $ \rho = \left| {\frac{{{q_{{v_{ij}}}}}}{{\sqrt {{q_{{v_i}}}{q_{{v_j}}}} }}} \right| $ | (6) |
经过实验,ρ>0.7定为两个统计量相关。
1.2.4 偏相关系数的检验对于两个统计量相关的观测值Li和Lj,为了进一步确定Li和Lj中哪一个含有粗差,引入对偏相关系数的检验。假设初步确定含有m个粗差,分别为L1、L2、…、Li、…Lm,而Lm+1、Lm+2、…、Lj、…Ln不含粗差,构造统计量[11]:
| $ F = \left| {\frac{{{T_{m - 1}} - {T_m}}}{{{T_m}/\left( {n - m} \right)}}} \right| \sim F\left( {1,n - m} \right) $ | (7) |
式中,
当F<Fα(1, n-m)时,观测值Li不含粗差; 否则,观测值Li含粗差。
2 多维粗差定位算法多维粗差定位算法流程:
1) 对所有观测值进行LS平差,对平差模型按式(1)进行整体检验。若检验通过,观测值中不含粗差,结束; 否则,观测值中可能含有粗差。
2) 计算标准化残差值wi,取wi最大值wmax对应的观测值Li按式(2)进行u检验。若检验通过,则继续步骤5) ~ 8)。
3) 若未通过检验,根据式(6)依次计算观测值Li对应的统计量wmax与第j(j≠i)个观测值Lj对应的统计量wj之间的相关系数ρ。若ρmax>0.7,将wmax对应的观测值Li存入列表A,将ρmax对应的观测值Lj存入列表B,同时剔除观测值Li和Lj; 若ρmax≤0.7,仅将wmax对应的观测值Li存入列表C,同时剔除观测值Li。
4) 重新对剩余的观测值进行LS平差。重复步骤2)和步骤3),直到u检验通过。
5) 经过前面几步,可以得到一些怀疑含有粗差的观测值:观测值对应的统计量具有相关性的分别存放在列表A和B中,不具有相关性的存放在列表C中。分别对列表A和列表B中的观测值根据式(7)进行偏相关系数的F检验。若检验通过,说明该观测值不含粗差,将其恢复到“可靠”观测值中; 若未通过检验,将其添加到列表Gross中。
6) 若列表A和B中的观测值检验完成,则清空列表A和B; 若未完成,则重复步骤5)。
7) 每次从列表C中取出一个观测值Li,与前面几步确定的所有不含粗差的“可靠”观测值进行LS平差,对观测值Li进行单独的u检验。若检验通过,说明之前是误判,将该观测值恢复到不含粗差的观测值中; 若检验未通过,说明Li是粗差,将其添加到列表Gross中,直到完成对列表C中观测值的检验。
8) 对剩下的所有不含粗差的观测值重新进行整体检验,即重复步骤1) ~8)。
3 粗差估值假设有n个观测值,t个必要观测值,经过粗差定位后,确定有m个粗差,且m < n-t,则m个含有粗差的观测值的误差方程可写为:
| $ {\mathit{\boldsymbol{V}}_g} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_g}}&\mathit{\boldsymbol{E}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}\\ {{{\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}}_g}} \end{array}} \right] - {\mathit{\boldsymbol{l}}_g} $ | (8) |
式中,Vg为m×1阶残差向量,Bg为m×t阶系数矩阵,E为m×m阶单位矩阵,
| $ {\mathit{\boldsymbol{V}}_r} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_r}}&{\bf{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}\\ {{{\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}}_g}} \end{array}} \right] - {\mathit{\boldsymbol{l}}_r} $ | (9) |
|
图 1 IBFS算法流程图 Fig. 1 The flow chart of IBFS algorithm |
式中,Vr为(n-m)×1阶残差向量,Br为(n-m)×t阶系数矩阵,0为(n-m)×m阶零矩阵,lr为(n-m)×1阶误差方程常数项。令
| $ \mathit{\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_g}}\\ {{\mathit{\boldsymbol{V}}_r}} \end{array}} \right],\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_g}}&\mathit{\boldsymbol{E}}\\ {{\mathit{\boldsymbol{B}}_r}}&{\bf{0}} \end{array}} \right],\mathit{\boldsymbol{\hat K}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}\\ {{{\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}}_g}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{l}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{l}}_g}}\\ {{\mathit{\boldsymbol{l}}_r}} \end{array}} \right],\mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_g}}&{\bf{0}}\\ {\bf{0}}&{{\mathit{\boldsymbol{P}}_r}} \end{array}} \right] $ |
则可合并为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{A\hat K}} - \mathit{\boldsymbol{l}} $ | (10) |
式中,A为n×(t+m)阶矩阵,
在VTPV =min的约束条件下,按照求函数极值的方法,可得:
| $ \mathit{\boldsymbol{\hat K}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} $ | (11) |
式中,
观测值经过改正后,常数项为:
| $ \mathit{\boldsymbol{\bar l}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{l}}_g}}\\ {{\mathit{\boldsymbol{l}}_r}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}}_g}}\\ {\bf{0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{l}}_g} - {{\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}}_g}}\\ {{\mathit{\boldsymbol{l}}_r}} \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_g}}\\ {{\mathit{\boldsymbol{B}}_r}} \end{array}} \right] $ | (12) |
误差方程为:
| $ \mathit{\boldsymbol{\bar V}} = \mathit{\boldsymbol{B\bar X}} - \mathit{\boldsymbol{\bar l}} $ | (13) |
式中,
| $ \mathit{\boldsymbol{\bar X = }}{\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P\bar l}} $ | (14) |
单位权中误差估值为:
| $ {\hat \sigma _0} = \sqrt {\frac{{{{\mathit{\boldsymbol{\bar V}}}^{\rm{T}}}\mathit{\boldsymbol{P\bar V}}}}{{n - t}}} $ | (15) |
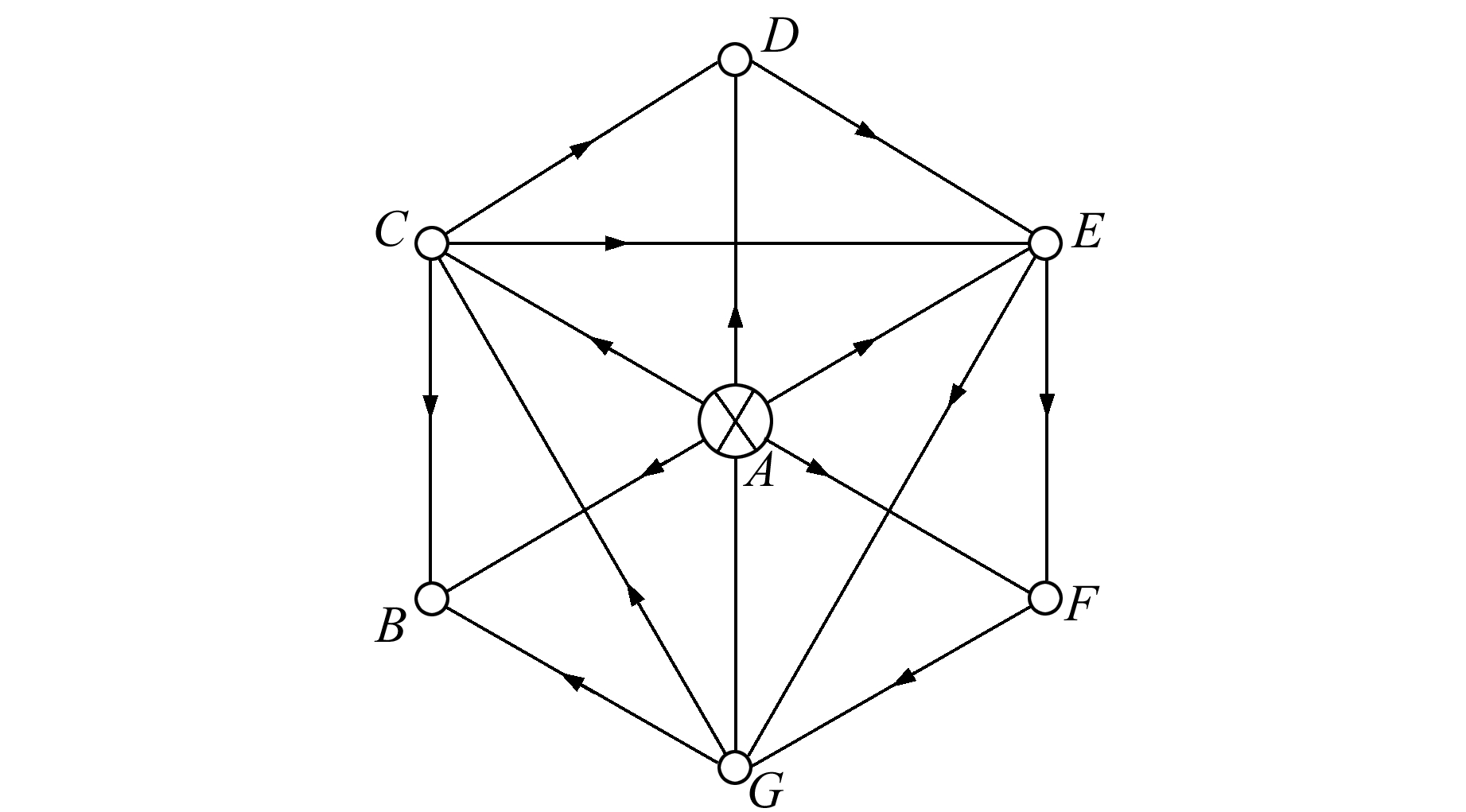
使用文献[12]中水准网数据,采用VC#编程验证算法的可行性。图 2所示的水准网中,A为已知点,B、C、D、E、F、G为待定点,其中有15个高差观测值,有9个多余观测值,A点高程为800.156 0 m,每km观测高差中误差为±1 mm。
|
图 2 水准网示意图 Fig. 2 Diagram of the leveling network |
|
|
表 1 水准网观测数据 Tab. 1 Observation data in the leveling network |
表 2(单位mm)给出模拟1、2、3、4、5、6个粗差的具体情况,其中1个粗差模拟为较小的粗差,2个粗差模拟为1个大粗差和1个小粗差,3个粗差模拟为3个小粗差,4个粗差模拟为2个大粗差和2个中等大小的粗差,5个粗差模拟为1个小粗差、1个较大粗差和3个大粗差,6个粗差模拟为3个小粗差和3个大粗差,同时也给出了按式(11)计算的粗差估值。表 3给出了粗差定位结果。
|
|
表 2 模拟的粗差及其估值 Tab. 2 The simulated gross errors and the evaluation of gross errors |
由表 3可知,BFS法、文献[6]方法在含有1个、2个、6个粗差时,定位结果完全正确,而文献[13]方法仅在含有6个粗差时定位正确。由此可见,BFS法、文献[6]方法略优于文献[13]方法。文献[13]方法虽然原理简单、较易实现,但粗差的定位结果取决于粗差搜索结束阈值的选择,而且有时也会出现转移粗差和图相关粗差的情况[14],影响粗差定位的结果。而BFS方法由于未顾及观测值构成的统计量相关性对粗差定位的影响,故定位结果不如考虑此因素的IBFS法。文献[6]和文献[13]方法在定位粗差时会出现漏判和错判现象,而IBFS法则通过向后-向前方式避免了出现弃真和纳伪错误,提高了定位的准确性。表 4给出具有统计量相关观测值的F检验值。
|
|
表 3 不同粗差探测方案的定位结果对比 Tab. 3 Comparison of location results of different gross error detection schemes |
|
|
表 4 具有统计量相关的观测值的F检验值 Tab. 4 F test values with statistical correlation observations |
1) 当观测值中存在多个粗差,且构建的统计量之间相关时,传统的数据探测法和向后-向前选择法无法正确实现粗差定位,容易犯第3类错误(粗差转移),而改进的向后-向前选择法保留了向后-向前选择法的优点,并避免弃真错误和纳伪错误。
2) 为了能够探测较小的粗差,通常需要在向后选择阶段适当增大显著性水平,以增加纳伪概率、降低弃真概率; 而在向前选择过程中可以适当降低显著性水平,来降低纳伪概率,两种方式组合可以实现很好的粗差探测效果。根据实验,在向后选择过程中显著性水平取α=0.10,向前选择过程中显著性水平取α=0.01,可以实现较好的粗差定位效果。
3) 实验表明,加入模拟的5个粗差(1个小粗差、2个较大粗差和3个大粗差),本文算法也能很好地探测出小的粗差,说明本文算法在多个粗差同时存在的情况下,即使有大粗差可能掩盖小粗差的情况,也非常有效。推导的粗差估值公式比较严密,且粗差估值也比较准确。
| [1] |
於宗俦, 李明峰. 多维粗差的同时定位与定值[J]. 武汉测绘科技大学学报, 1996(4): 17-23 (Yu Zongchou, Li Mingfeng. Simultaneous Location and Evaluation of Multidimensional Gross Errors[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1996(4): 17-23)
(  0) 0) |
| [2] |
施闯, 刘经南. 基于相关分析的粗差理论[J]. 武汉测绘科技大学学报, 1998(1): 7-11 (Shi Chuang, Liu Jingnan. Correspondence Based Outlier Analysis[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998(1): 7-11)
(  0) 0) |
| [3] |
陈玮娴, 袁庆. 抗差总体最小二乘方法[J]. 大地测量与地球动力学, 2012, 32(6): 111-113 (Chen Weixian, Yuan Qing. A Robust Total Least-Squares Method[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 111-113)
(  0) 0) |
| [4] |
王建民, 张锦, 苏巧梅. 观测数据中的粗差定位与定值算法[J]. 武汉大学学报:信息科学版, 2013, 38(10): 1 225-1 228 (Wang Jianmin, Zhang Jin, Su Qiaomei. Algorithm for Location and Evaluation of Gross Errors in Surveying Data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10): 1 225-1 228)
(  0) 0) |
| [5] |
刘陶胜, 黄声享, 李沛鸿. 基于双极差的粗差探测方法研究[J]. 大地测量与地球动力学, 2012, 32(1): 80-83 (Liu Taosheng, Huang Shengxiang, Li Peihong. Research on Gross Error Detection Based on Bio-Pole Method[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 80-83)
(  0) 0) |
| [6] |
金丽宏, 汪耀, 崔太岷, 等. 基于均值漂移模型的粗差定值定位[J]. 测绘科学, 2017, 42(8): 19-23 (Jin Lihong, Wang Yao, Cui Taimin, et al. The Location and Evaluation of Gross Error Based on the Mean Shift Model[J]. Science of Surveying and Mapping, 2017, 42(8): 19-23)
(  0) 0) |
| [7] |
吴祖海, 罗伟钊, 李军. 坐标转换中公共点粗差定位与降低粗差点影响方法研究[J]. 大地测量与地球动力学, 2014, 34(1): 118-122 (Wu Zuhai, Luo Weizhao, Li Jun. On Position of Gross Errors of Common Points in Coordinate Transformation and Reducing Influence of Gross Errors[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 118-122)
(  0) 0) |
| [8] |
杨元喜, 吴富梅. 临界值可变的抗差估计等价权函数[J]. 测绘科学技术学报, 2006(5): 317-320 (Yang Yuanxi, Wu Fumei. Modified Equivalent Weight Function with Variable Criterion for Robust Estimation[J]. Journal of Geomatics Science and Technology, 2006(5): 317-320 DOI:10.3969/j.issn.1673-6338.2006.05.002)
(  0) 0) |
| [9] |
刘宸, 刘长建, 王赛, 等. 两种新的IGGⅢ改进方案[J]. 测绘通报, 2016(10): 54-57 (Liu Chen, Liu Changjian, Wang Sai, et al. Two New Improvements of IGGⅢ Scheme[J]. Bulletin of Surveying and Mapping, 2016(10): 54-57)
(  0) 0) |
| [10] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2014 (Survey Adjustment Group in School of Geodesy and Geomatics of Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2014)
(  0) 0) |
| [11] |
陶本藻, 姚宜斌, 施闯. 基于相关分析的粗差可区分性[J]. 武汉大学学报:信息科学版, 2004(10): 881-884 (Tao Benzao, Yao Yibin, Shi Chuang. Distinguishability of Outlier Based on Correlative Analysis[J]. Geomatics and Information Science of Wuhan University, 2004(10): 881-884)
(  0) 0) |
| [12] |
葛永慧. 再生权最小二乘法稳健估计[M]. 北京: 科学出版社, 2015 (Ge Yonghui. Research on Self-Born Weighted Least Squares Method[M]. Beijing: Science Press, 2015)
(  0) 0) |
| [13] |
王爱生, 欧吉坤. 部分最小二乘平差方法及在粗差定值与定位中的应用[J]. 测绘科学, 2005(2): 70-72 (Wang Aisheng, Ou Jikun. Method of Partly Least Squares and Application in Gross Error Location and Estimation[J]. Science of Surveying and Mapping, 2005(2): 70-72 DOI:10.3771/j.issn.1009-2307.2005.02.021)
(  0) 0) |
| [14] |
陈振杰, 蒋辉. 粗差定位定值方法在EDM三角高程测量数据处理中的应用[J]. 江苏测绘, 2002(1): 3-6 (Chen Zhenjie, Jiang Hui. The Application of Locating and Estimating of Gross Error in DEM Trigonometric Leveling[J]. Jiangsu Surveying and Mapping, 2002(1): 3-6)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


