在大坝变形预测中,BP神经网络模型等[1-2],被广泛应用。但是,BP收敛速度慢,易陷入局部极值,隐层和隐层节点个数选取困难[3]。PSO标准粒子群算法具有良好的参数寻优能力,可以用来优化BP的权值和阈值,提高网络预测精度[4],但算法早熟收敛,可能不能获得最优结果。为此,对粒子群的惯性权重进行改进,使PSO-BP模型更易寻找到最优解,如线性惯性权重策略[5](LDIW)、随机惯性权重策略[6](RIW)和模糊惯性策略[7](FIW)等改变惯性权重的方法,均使精度得到一定程度的提高。赵志刚等[8]提出自适应惯性权重均值粒子群算法,提高了算法的全局搜索能力。本文基于粒子群和BP神经网络算法,提出一种加入变异操作的自适应粒子群神经网络模型,弥补BP网络和粒子群算法的不足,提高全局搜索能力,实现了大坝形变的精准预测。
1 标准粒子群优化BP网络算法 1.1 粒子群算法原理粒子群算法是模拟鸟群觅食行为。粒子以一定的速度在D维空间飞行,期间由飞行经验和同伴飞行经验实现对速度的动态调整,更新粒子位移。在搜索过程中,粒子i依据目标函数的适应度评价粒子好坏,确定当前粒子的个体极值pid和全局极值pgd。粒子群的速度更新公式为:
| $ \begin{align} & v_{id}^{(k+1)}=w\cdot v_{id}^{k}+c\cdot \\ & \text{rand}[({{p}_{id}}-x_{id}^{k})+({{p}_{gd}}-x_{id}^{k})] \\ \end{align} $ | (1) |
式中第1项是物体的运动惯性项,第2项是粒子对历史位置的记忆认知能力,第3项是粒子的社会认知,实现群体信息的共享。上式表明,粒子有向个体极值和群体极值方向移动的趋势。
粒子群位置更新公式为:
| $ x_{id}^{k+1}=x_{id}^{k}+v_{id}^{k+1} $ | (2) |
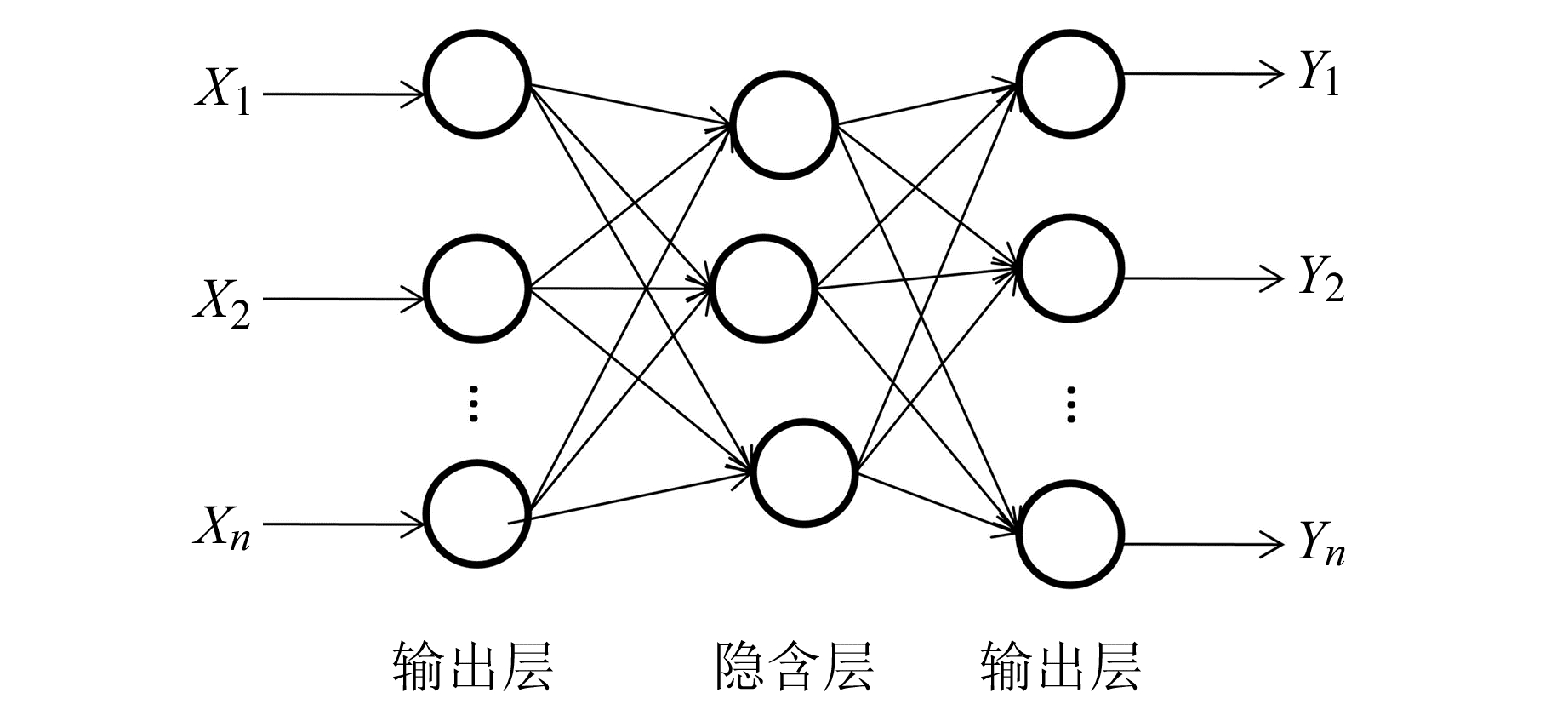
选用3层BP神经网络,包括输入层
|
图 1 3层神经网络 Fig. 1 Three layered neural network |
为提高粒子群算法性能,Shi等引入惯性权重w,即公式(1),此即标准粒子群算法。
经典粒子群优化BP网络中,粒子的惯性权重为一定值。在算法设计中,需要先确定BP网络结构和参数,进而确定PSO算法的粒子长度,即维度。在确定BP网络后,设置PSO参数(迭代次数、种群规模等)和目标函数(视问题而定)及前后迭代适应度之差的限值。PSO-BP模型确定后初始化BP网络,提取BP网络权值和阈值,利用PSO算法将其优化,并赋予BP网络,输入样本数据进行BP网络预测,进入迭代过程。当迭代误差小于阈值时,输出预测结果。
2 改进的PSO算法经典PSO-BP神经网络中,PSO算法早熟收敛且受惯性权重影响较大。算法前期需要较大的权值来提高全局搜索能力,后期需要较小的权值以防止陷入局部极值[10]。因此,随着迭代步数的增加,需要减小惯性权重。与经典PSO-BP不同,线性粒子群算法采用惯性权重线性递减权值的策略[11],自适应粒子群则采用非线性动态惯性权重系数公式[12]。
2.1 线性粒子群算法线性粒子群的权值调整公式如下:
| $ w={{w}_{\text{max}}}-\frac{R({{w}_{\text{max}}}-{{w}_{\text{min}}})}{{{R}_{\text{max}}}} $ | (3) |
其中,wmax、wmin为设定的最大、最小惯性权重,R是粒子当前迭代次数,Rmax是最大迭代步数。线性粒子群即是在粒子群参数确定的基础上,线性调整权值,更新粒子速度和位置,在搜索范围内得到最佳值。
2.2 改进的自适应粒子群算法PSO搜索过程是高度复杂且非线性的,线性递减权重策略并不适于这种优化搜索过程,改用非线性权重递减策略可以提高预测精度[13]:
| $ w=\left\{ \begin{align} & {{w}_{\text{min}}}-\frac{({{w}_{\text{max}}}-{{w}_{\text{min}}})(f-{{f}_{\text{min}}})\text{ }}{{{f}_{\text{avg}}}-{{f}_{\text{min}}}}, \ \ \ \ f\le {{f}_{\text{avg}}} \\ & {{w}_{\text{max}}}\text{, }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ }f>{{f}_{\text{avg}}}\text{ }\!\!~\!\!\text{ } \\ \end{align} \right.\text{ } $ | (4) |
式中, f是粒子当前的适应度值,favg和fmin分别是当前所有粒子的平均和最小适应度值。通过判断粒子的离散程度,来动态改变粒子的惯性权重。当粒子的适应度值比较分散时,减小惯性权重; 比较一致时,增加惯性权重。在迭代计算中,粒子速度更新公式中随机项rand大于0.95时,粒子搜索能力降低。为了提高搜索能力,加入自适应变异,初始化这些粒子某个维度的值。改进后的算法非线性调整粒子权重,而且加入自适应变异,其全局搜索能力增强,不易陷入局部最优。
3 BP网络设计 3.1 BP参数确定本文采用3层BP神经网络,隐含层节点个数为[14]:
| $ H_{m} <N_{I}-1 $ | (5) |
| $ {{H}_{m}} <\sqrt{{{O}_{m}}+{{N}_{I}}}+a $ | (6) |
| $ {{H}_{m}}=\text{lo}{{\text{g}}_{2}}{{N}_{I}}~ $ | (7) |
式中,Hm为隐含层节点数,NI为输入层节点数,Om是输出层个数,a是0~10之间的常数。本文中输入层节点有8个,输出层节点1个,采用试凑法确定隐含层节点为6个,网络结构为8-6-1型。
3.2 BP算法流程1) 初始化神经网络参数,设置输入层节点数8个、隐含层节点数6个和输出层节点1个,并随机初始化网络的权阈值。
2) 选取tan-sigmoid函数为隐含层传递函数,pureline函数为输出层传递函数,以实现任意非线性函数的映射。设置训练函数为traing-dx(自适应学习速率动量梯度下降反向传播算法),最大训练步数1 000,训练目标0.000 01,学习速率0.01,附加动量因子0.9,训练截止次数20次。
3) 归一化训练数据和目标数据并输入BP网络,计算输出值与期望值之差并反向传播,更新权值和阈值,判断输出目标是否达到终止条件,否则重复步骤3)。
4) 输入测试数据,输出预测值,并与期望值比较,对此次预测结果进行精度评价。
4 改进自适应PSO-BP优化神经网络改进自适应粒子群中加入了变异算子,权重非线性递减。设置粒子群种群规模为100,速度区间[-1, 1],位置区间[-5, 5],最大迭代次数100,学习率c1=c2=1.5。根据适应度函数不断迭代,评选出个体最佳和群体最佳位置,更新粒子的速度和位置。
改进粒子群算法和神经网络算法确定后,通过BP算法中权值和阈值将两种模型连接,即为ADPPSO-BP组合模型。为此,必须对粒子进行编码,计算出粒子的长度。在寻找最优值时,粒子群的评价函数直接影响最佳最优粒子,从而影响BP网络预测的精度。为使结果更接近真实值,本文选用与BP网络相适应的均方根误差作为适应度函数。
改进自适应PSO-BP网络算法步骤如下:
1) 确定粒子的编码长度:M=inputnum×hiddennum+hiddennum×2+1=61,粒子位置参数为神经网络的权值或阈值,编码长度是粒子维度。
2) 确定适应度函数。采用均方根误差作为粒子的适应度函数,评价粒子的“优劣”。
3) 为了加快数据处理速度和提高预测精度,对建模数据进行归一化处理。调用MATLAB神经网络命令newff建立网络,train函数进行网络训练,将训练结果反归一化处理并调整权阈值,完成模型训练。提取BP网络权阈值作为粒子群初始位置参数,开始寻优迭代。经过优化后的权值阈值赋给BP网络,进行网络预测,进一步调整权阈值,使得均方根误差小于设定的目标期望值,建立改进自适应PSO-BP模型。
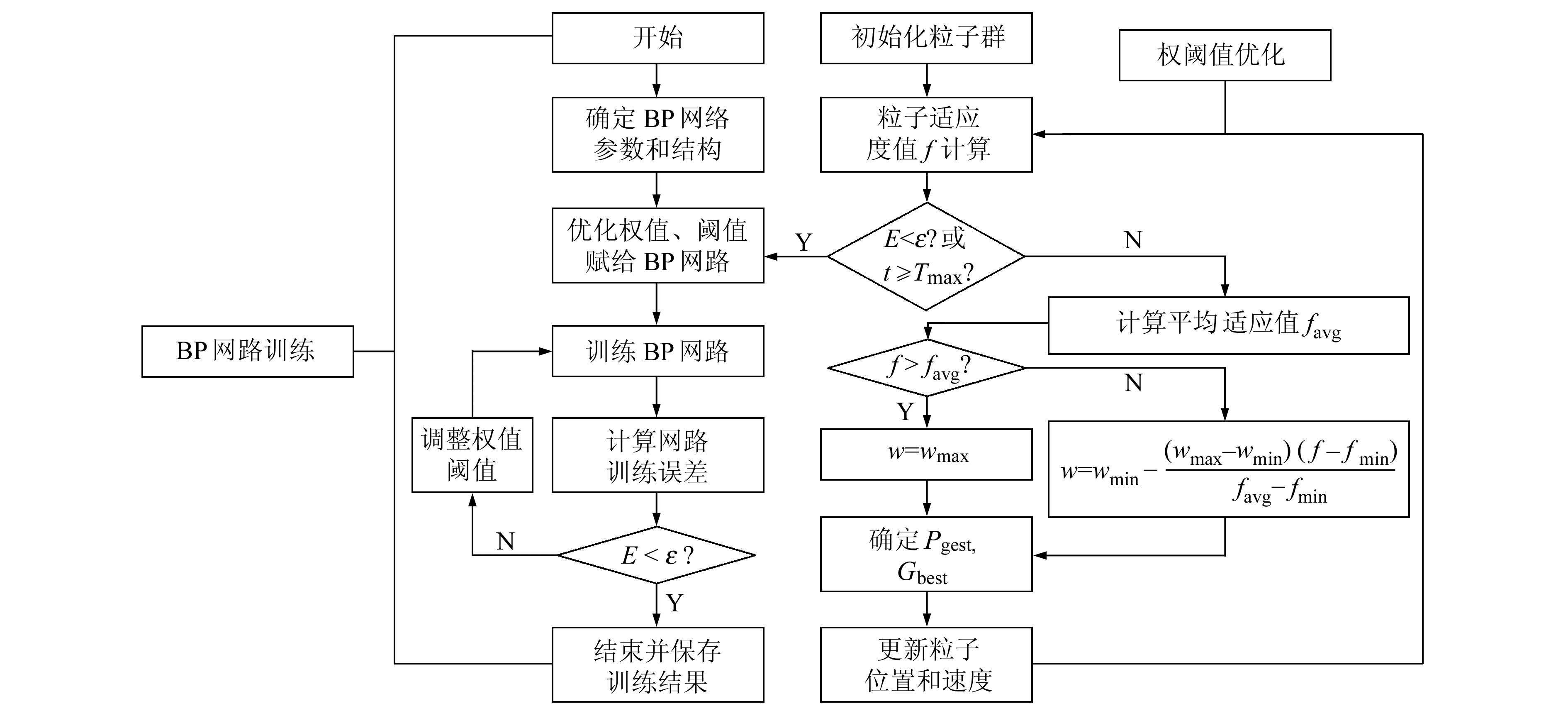
模型确定后,算法实现程序如图 2所示。
|
图 2 改进ADPPSO-BP算法流程 Fig. 2 Algorithm implementation scheme of improved ADPPSO-BP |
实验数据为丰满大坝30#坝段监测成果[15],包括水平变形、同期观测水位值、温度以及时间效应量。选取1985-03-22~1987-04-24共120组数据作为原始数据进行预测分析。
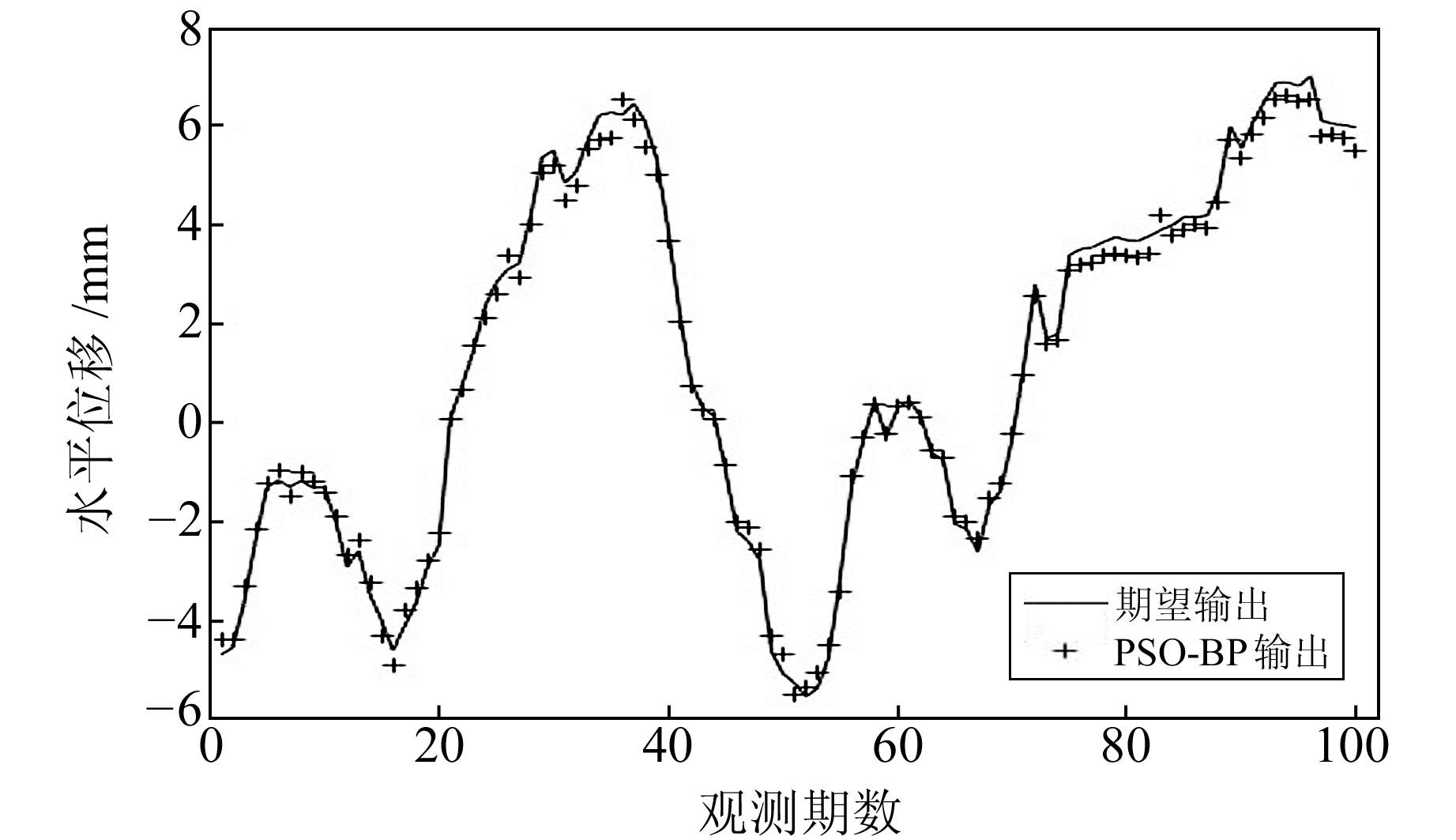
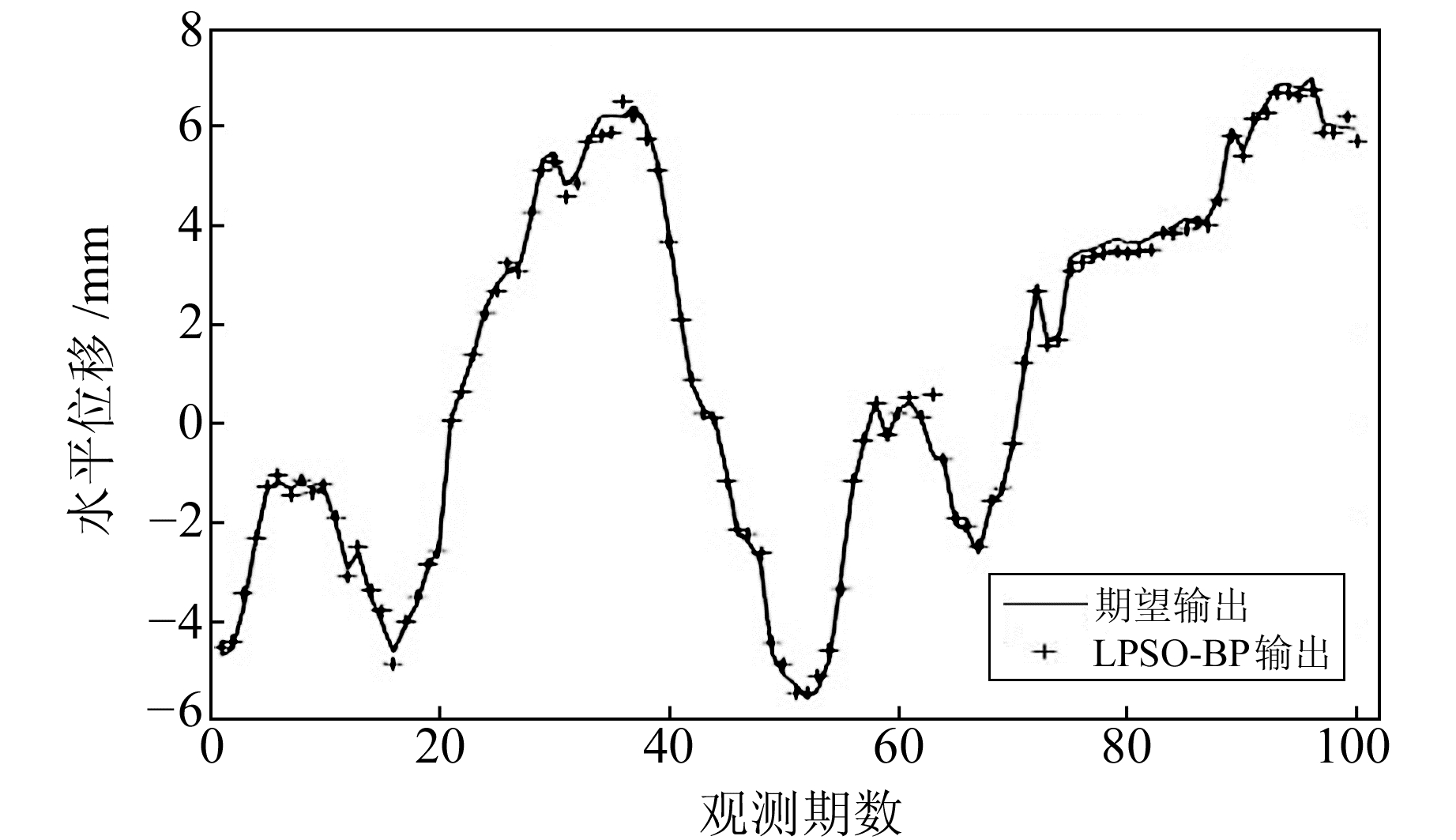
5.1 BP网络训练及结果输出选取前100个数据作为训练数据,采用传统的粒子群优化BP神经网络模型、线性递减惯性权重优化神经网络模型、改进的自适应权重粒子群优化BP算法训练数据,结果如图 3~5所示。由图可见,ADPPSO-BP的拟合程度最高,LPSO-BP次之,PSO-BP误差较大。
|
图 3 PSO-BP结果与期望对比 Fig. 3 PSO-BP results is compared with the expectation |
|
图 4 LPSO-BP结果与期望对比 Fig. 4 LPSO-BP results is compared with the expectation |
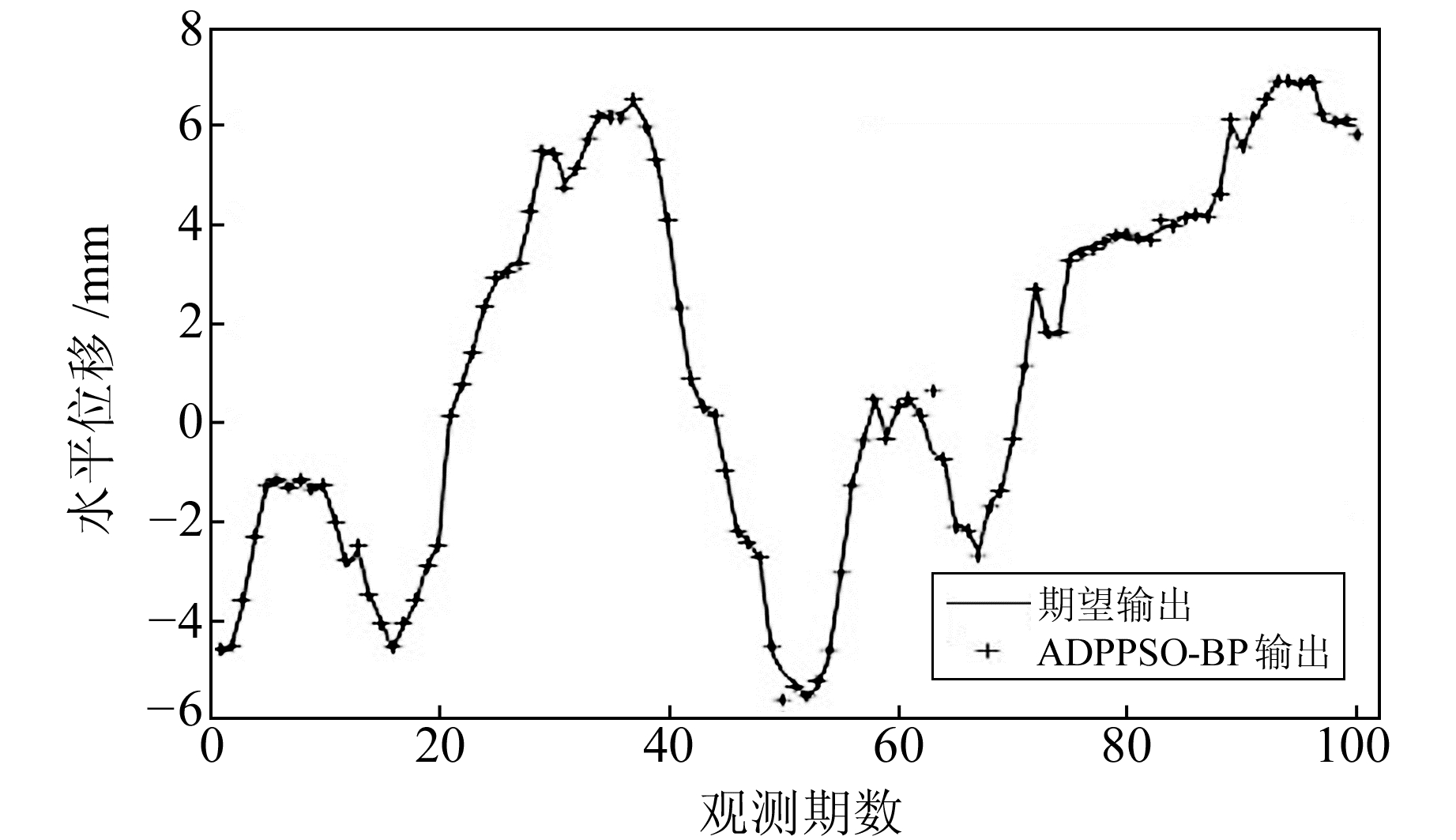
|
图 5 ADPPSO-BP与期望输出对比 Fig. 5 ADPPSO-BP results is compared with the expectation |
将3种模型的拟合误差进行对比,如图 6、图 7。由图 6可知,PSO-BP较LPSO-BP波动大,在值域区间[-0.4,0.5]更加离散,LPSO-BP预测值更集中在0值附近,表明LPSO-BP预测优于传统的PSO-BP预测。ADPPSO-BP在值域范围比LPSO-BP算法表现得更加平稳且更集中在0值附近。可见,ADPPSO-BP模型预测精度最高、预测最准确,LPSO-BP次之,PSO-BP最差。
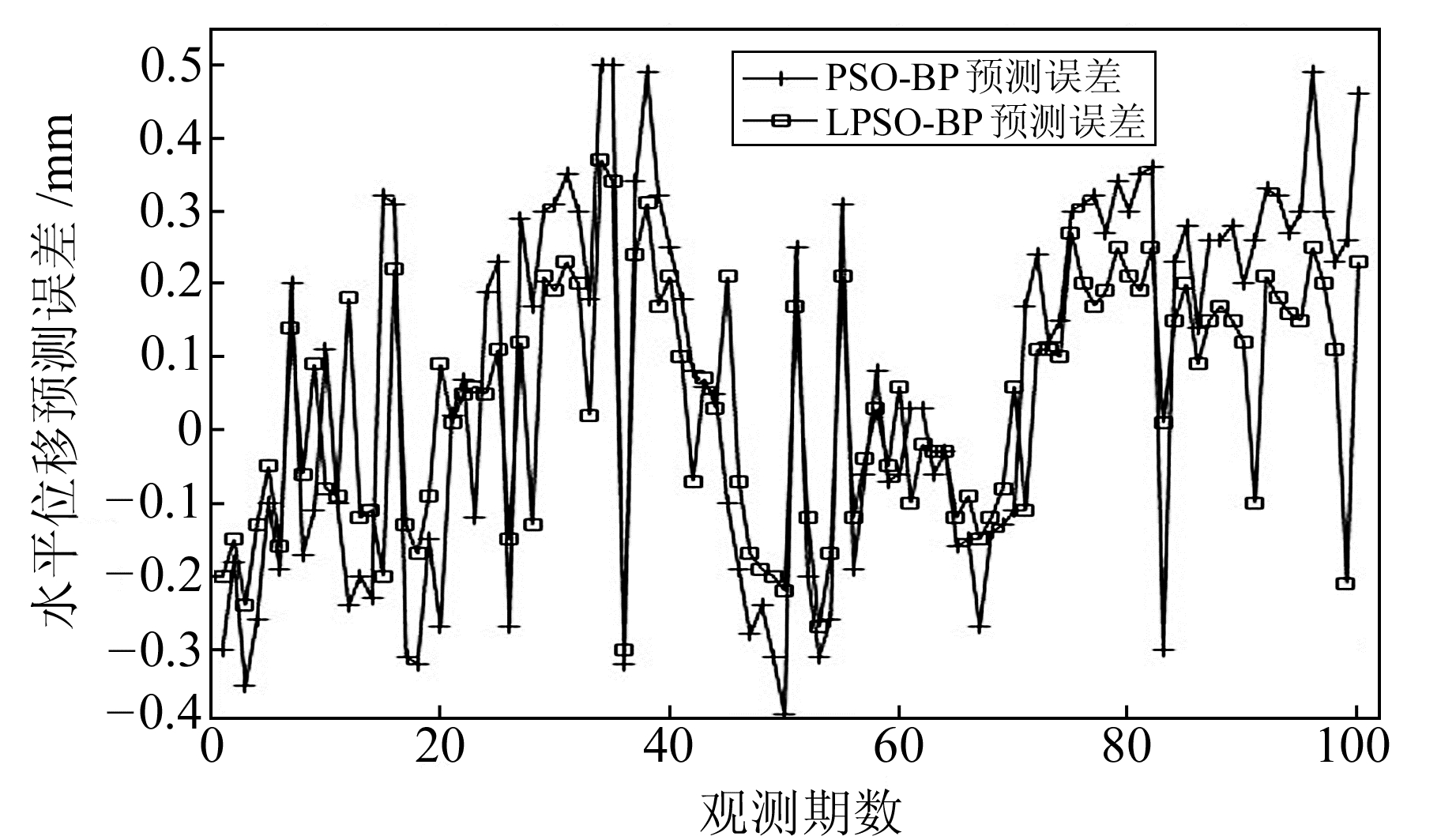
|
图 6 LPSO-BP与PSO-BP仿真对比 Fig. 6 Simulation comparison between LPSO-BP and PSO-BP |
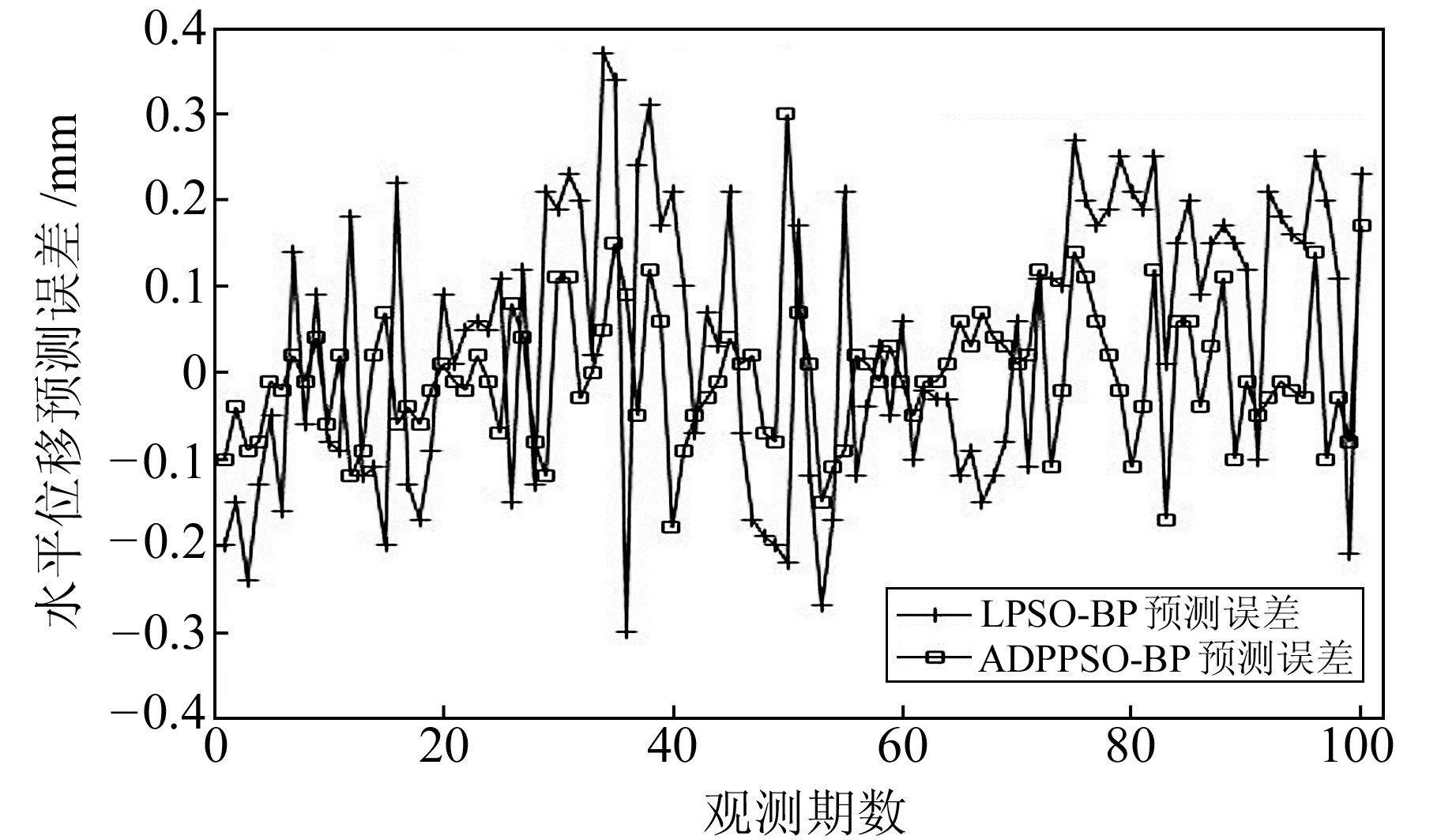
|
图 7 LPSO-BP与ADPPSO-BP仿真对比 Fig. 7 Simulation comparison between LPSO-BP and ADPPSO-BP |
输入后20组样本数据,用标准PSO-BP、LPSO-BP和改进ADPPSO-BP模型进行预测模拟,结果见表 1。可以看出,PSO-BP预测相对误差绝对值集中在7%~8%,个别达到9%、11%、12%;20号样本预测误差最大,达到-15.38%,中误差为0.25 mm。LPSO-BP相对误差绝对值集中在5%~6%,个别误差在7%和8%左右; 20号样本误差为10.26%,略小于第一种,中误差为0.21 mm,说明PSO-BP和LPSO-BP对小值数据预测精度较差。ADPPSO-BP相对误差绝对值大部分在5%以内,少数样本误差集中在5%~6%,其中20号样本预测的相对误差为5.31%,中误差0.15 mm。相较于前两种模型,预测精度有很大提高,小值数据也可以精确预测。
|
|
表 1 PSO-BP、LPSO-BP、ADPPSO-BP仿真预测对比 Tab. 1 System simulation comparison among PSO-BP, LPSO-BP and ADPPSO-BP |
本文改进自适应惯性权重粒子群,并通过实例建模与PSO-BP、LPSO-BP进行比较。实验表明,线性惯性权重的预测精度比PSO-BP有所提高,但对于小值数据预测不太理想。自适应粒子群加入变异算子优化后的BP网络克服了小值数据的预测误差,大大提高了预测精度。
| [1] |
任超, 梁月吉, 庞光锋, 等. 基于灰色最小二乘支持向量机的大坝变形预测[J]. 大地测量与地球动力学, 2015, 35(4): 608-612 (Ren Chao, Liang Yueji, Pang Guangfeng, et al. Dam Deformation Prediction Based on Grey Least Square Support Vector Machines[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 608-612)
(  0) 0) |
| [2] |
王勇, 张立辉, 杨晶. 基于BP神经网络的对流层延迟预测研究[J]. 大地测量与地球动力学, 2011, 31(3): 134-137 (Wang Yong, Zhang Lihui, Yang Jing. Study on Prediction of Zenith Tropospheric Delay by Use of BP Neural Network[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 134-137)
(  0) 0) |
| [3] |
王小辉, 王琪洁, 丁元兰, 等. 基于二次曲面和BP神经网络组合模型的GPS高程异常拟合[J]. 大地测量与地球动力学, 2012, 32(6): 103-105 (Wang Xiaohui, Wang Qijie, Ding Yuanlan, et al. Combined Model in Height Anomaly Fitting[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 103-105)
(  0) 0) |
| [4] |
徐锋, 王崇倡, 张飞. 粒子群-BP神经网络模型在大坝变形监测中的应用[J]. 测绘科学, 2012, 37(4): 181-183 (Xu Feng, Wang Chongchang, Zhang Fei. Application of Particle Swarm Optimization-BP Neutral Network in Dam Displacement Prediction[J]. Science of Surveying and Mapping, 2012, 37(4): 181-183)
(  0) 0) |
| [5] |
Shi Y H, Eberhart R C. Empirical Study of Particle Swarm Optimization[J]. Journal of System Simulation, 1999, 3(1): 31-37
(  0) 0) |
| [6] |
Eberhart R C, Shi Y. Tracking and Optimizing Dynamic Systems with Particle Swarms[C]. The 2001 Congress on Evolutionary Computation, 2001
(  0) 0) |
| [7] |
Shi Y, Eberhart R C. Fuzzy Adaptive Particle Swarm Optimization[C]. The 2001 Congress on Evolutionary Computation, 2001
(  0) 0) |
| [8] |
赵志刚, 林玉娇, 尹兆远. 基于自适应惯性权重的均值粒子群优化算法[J]. 计算机工程与科学, 2016, 38(3): 501-506 (Zhao Zhigang, Lin Yujiao, Yin Zhaoyuan. A Mean Particle Swarm Optimization Algorithm Based on Adaptive Intertia Weight[J]. Computer Engineering & Science, 2016, 38(3): 501-506 DOI:10.3969/j.issn.1007-130X.2016.03.016)
(  0) 0) |
| [9] |
朱明晨, 赵平, 陈伟荣. 基于BP神经网络的霍普菲尔德模型改进研究[J]. 测绘工程, 2016, 25(9): 26-30 (Zhu Mingchen, Zhao Ping, Chen Weirong. Improved Research for Hopflied Model Based on BP Neural Network[J]. Engineering of Surveying and Mapping, 2016, 25(9): 26-30)
(  0) 0) |
| [10] |
秦立龙, 王振宇. 改进粒子群算法在调制模式识别中的应用[J]. 计算机工程与科学, 2013, 35(7): 102-107 (Qin Lilong, Wang Zhenyu. Improved Particle Swarm Optimization Algorithm and Its Application in Modulation Recognition[J]. Computer Engineering & Science, 2013, 35(7): 102-107 DOI:10.3969/j.issn.1007-130X.2013.07.017)
(  0) 0) |
| [11] |
Shi Y, Eberhart R. A Modified Partide Swarm Optimizer[C]. IEEE International Conference on Evolutionary Computation, Anchorage A K, 1998.
(  0) 0) |
| [12] |
温正, 孙华克. MATLAB智能算法[M]. 北京: 清华大学出版社, 2017 (Wen Zheng, Sun Huake. MATLAB Intelligent Algorithom[M]. Beijing: Tsinghua University Press, 2017)
(  0) 0) |
| [13] |
董红斌, 李冬锦, 张小平. 一种动态调整惯性权重的粒子群优化算法[J]. 计算机科学, 2018, 45(2): 98-102 (Dong Hongbin, Li Dongjin, Zhang Xiaoping. Particle Swarm Optimization Algorithm with Dynamically Adjusting Inertia Weight[J]. Computer Science, 2018, 45(2): 98-102)
(  0) 0) |
| [14] |
齐银峰, 谭荣建. 基于改进粒子群优化算法的BP神经网络在大坝变形分析中的应用[J]. 水利水电技术, 2017, 48(2): 118-124 (Qi Yinfeng, Tan Rongjian. Application of Improved Particle Swarm Optimization Algorithm-Based BP Neural Network to Dam Deformation Analysis[J]. Water Resources and Hydropower Engineering, 2017, 48(2): 118-124)
(  0) 0) |
| [15] |
姜成科.基于遗传算法的神经网络在大坝变形预报中的应用[D].大连: 大连理工大学, 2009 (Jiang Chengke.Application of Neutral Network Based on Genetic Algorithm in Dam Displacement Forecast[D]. Dalian: Dalian University of Technology, 2009) http://cdmd.cnki.com.cn/Article/CDMD-10141-2009040830.htm
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

