2. 西南交通大学地球科学与环境工程学院,成都市犀安路999号,611756;
3. 中国科学院国家授时中心,西安市书院东路3号,710600
精密单点定位(PPP)技术以其cm级甚至更高的定位精度广泛应用于低轨卫星精密定轨、地壳形变监测、GNSS气象学、海陆空不同载体的高精度定位、区域地震活动监测、时间传递等诸多领域[1-3]。PPP技术最大的问题是收敛时间太长,利用无电离层组合模型加上模糊度固定技术可以提高收敛速度,但对于采用频分多址技术的GLONASS系统,各种硬件偏差很难准确获取。目前提高PPP收敛速度的方法主要有2种,一是增加第3频率的观测值,如L5观测值[4],但这样会增加接收机成本;二是采用多系统组合定位[5-6]。通常情况下,多系统组合PPP的函数模型采用无电离层组合模型,随机模型按先验定权模型。无电离层组合模型放大了观测噪声,丢失了电离层信息,所以有学者提出采用非组合方式进行PPP解算[7]。但在非组合PPP中,将每个接收机-卫星对沿视线方向的电离层延迟作为参数同其他未知参数一并解算会导致解算的电离层参数过多,使方程的强度减弱,例如电离层延迟参数与接收机DCB高度相关[8],所以需要一种先验的电离层信息和接收机DCB来增强解决方案[8-9]。
本文在非组合PPP原始函数模型的基础上加上先验的电离层信息进行约束,随机模型采用Helmert方差分量估计,在3个系统之间定权,比较2种函数模型的差异。
1 理论方法与处理策略 1.1 组合定位原理 1.1.1 组合定位的函数模型对于双频GNSS接收机,无电离层组合模型的线性化观测方程可以表述为:
| $ \begin{gathered} P_{{\text{O}},{\text{r}},f}^{\text{s}} - P_{{\text{C}},{\text{r}},f}^{\text{s}} = \mathit{\boldsymbol{\mu }}_{\text{r}}^{\text{s}}\delta {\mathit{\boldsymbol{p}}_{\text{r}}} + \delta {t_{\text{r}}} + {M^{\text{s}}}\delta {T_{{\text{ztd}}}} + {\varepsilon _P} \hfill \\ L_{{\text{O}},{\text{r}},f}^{\text{s}} - P_{{\text{C}},{\text{r}},f}^{\text{s}} = \mathit{\boldsymbol{\mu }}_{\text{r}}^{\text{s}}\delta {\mathit{\boldsymbol{p}}_{\text{r}}} + \delta {t_{\text{r}}} + {M^{\text{s}}}\delta {T_{{\text{ztd}}}} + {\varepsilon _P} \hfill \\ \;\;\;\;\;\;\;\lambda _f^{\text{s}}\delta N_{{\text{r}},f}^{\text{s}} + {\varepsilon _L} \hfill \\ \end{gathered} $ | (1) |
式中,下标O和C分别代表在频率f上观测和计算的GNSS伪距(P)和载波相位(L);上标s和下标r分别代表GNSS系统(s=GPS,BDS,GLONASS)和接收机;
同样,基于原始观测值的非组合PPP模型的线性化观测方程可以表述为:
| $ \begin{array}{*{20}{c}} {P_{{\rm{O}},{\rm{r}},f}^{\rm{s}} - P_{{\rm{C}},{\rm{r}},f}^{\rm{s}} = \mathit{\boldsymbol{\mu }}_{\rm{r}}^{\rm{s}}\delta {\mathit{\boldsymbol{p}}_{\rm{r}}} + \delta {t_{\rm{r}}} + {M^{\rm{s}}}\delta {T_{{\rm{ztd}}}} + }\\ {\delta I_{{\rm{r}},f}^{\rm{s}} - {\gamma _f} \cdot {d_{{\rm{r}},{\rm{DCB}}}} + {\varepsilon _P}}\\ {L_{{\rm{O}},{\rm{r}},f}^{\rm{s}} - L_{{\rm{C}},{\rm{r}},f}^{\rm{s}} = \mathit{\boldsymbol{\mu }}_{\rm{r}}^{\rm{s}}\delta {\mathit{\boldsymbol{p}}_{\rm{r}}} + \delta {t_{\rm{r}}} + {M^{\rm{s}}}\delta {T_{{\rm{ztd}}}} - }\\ {\delta I_{{\rm{r}},f}^{\rm{s}} - \lambda _f^{\rm{s}}\delta N_{{\rm{r}},f}^{\rm{s}} + {\varepsilon _L}} \end{array} $ | (2) |
式中,
1) 高度角定权
卫星高度角可以间接反映观测值的精度。当高度角较低时,观测值受电离层、对流层、多路径等误差的影响较大,导致观测值精度降低。本文采用三角函数高度角模型对GNSS观测值进行定权,相应的伪距和载波方差为[10]:
| $ {\sigma ^2} = \left\{ {\begin{array}{*{20}{l}} {\frac{{\sigma _0^2}}{{\sin \theta }},}&{\theta \ge \alpha }\\ {\frac{{\sigma _0^2}}{{{{\sin }^2}\theta }},}&{\theta < \alpha } \end{array}} \right. $ | (3) |
式中,α为高度角阈值,一般设置为30°;θ为卫星高度角;σ02为观测值先验方差;σ为观测值方差。
2) 赫尔默特方差分量估计
对式(1)线性化,得到误差方程(权阵为P):
| $ \boldsymbol{V}=\boldsymbol{A} \hat{x}-\boldsymbol{L} $ | (4) |
系统内观测值权阵按照式(3)确定,分别设为PG、PC、PR,观测值残差分别设为VG、VC、VR,则法方程系数阵N和常数阵W分别为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}} = {{\left( {{\mathit{\boldsymbol{A}}^{\rm{G}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{G}}}{\mathit{\boldsymbol{A}}^{\rm{G}}} + {{\left( {{\mathit{\boldsymbol{A}}^{\rm{C}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{C}}}{\mathit{\boldsymbol{A}}^{\rm{C}}} + {{\left( {{\mathit{\boldsymbol{A}}^{\rm{R}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{R}}}{\mathit{\boldsymbol{A}}^{\rm{R}}} = }\\ {{\mathit{\boldsymbol{N}}^{\rm{G}}} + {\mathit{\boldsymbol{N}}^{\rm{C}}} + {\mathit{\boldsymbol{N}}^{\rm{R}}}} \end{array} $ | (5) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}} = {{\left( {{\mathit{\boldsymbol{A}}^{\rm{G}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{G}}}{\mathit{\boldsymbol{L}}^{\rm{G}}} + {{\left( {{\mathit{\boldsymbol{A}}^{\rm{C}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{C}}}{\mathit{\boldsymbol{L}}^{\rm{C}}} + {{\left( {{\mathit{\boldsymbol{A}}^{\rm{R}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{R}}}\mathit{\boldsymbol{v}}{\mathit{\boldsymbol{L}}^{\rm{R}}} = }\\ {{\mathit{\boldsymbol{W}}^{\rm{G}}} + {\mathit{\boldsymbol{W}}^{\rm{C}}} + {\mathit{\boldsymbol{W}}^{\rm{R}}}} \end{array} $ | (6) |
采用严密的Helmert方差分量估计的3系统观测值方差
| $ \hat{\boldsymbol{\theta}}=\boldsymbol{S}^{-1} \boldsymbol{W}_{\theta} $ |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{\rm{tr}}{{\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{G}}}} \right)}^2}}&{{\mathop{\rm tr}\nolimits} {{\left( {{\mathit{\boldsymbol{N}}^{\rm{G}}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{C}}}{\mathit{\boldsymbol{N}}^{ - 1}}} \right)}^2}}&{{\mathop{\rm tr}\nolimits} {{\left( {{\mathit{\boldsymbol{N}}^{\rm{G}}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{R}}}{\mathit{\boldsymbol{N}}^{ - 1}}} \right)}^2}}\\ {{\mathop{\rm tr}\nolimits} {{\left( {{\mathit{\boldsymbol{N}}^{\rm{C}}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{G}}}{\mathit{\boldsymbol{N}}^{ - 1}}} \right)}^2}}&{{\rm{tr}}{{\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{C}}}} \right)}^2}}&{{\mathop{\rm tr}\nolimits} {{\left( {{\mathit{\boldsymbol{N}}^{\rm{C}}}{\rm{v}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{R}}}{\mathit{\boldsymbol{N}}^{ - 1}}} \right)}^2}}\\ {{\rm{tr}}{{\left( {{\mathit{\boldsymbol{N}}^{\rm{R}}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{G}}}{\mathit{\boldsymbol{N}}^{^{ - 1}}}} \right)}^2}}&{{\rm{tr}}{{\left( {{\mathit{\boldsymbol{N}}^{\rm{R}}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{G}}}{\mathit{\boldsymbol{N}}^{^{ - 1}}}} \right)}^2}}&{{\rm{tr}}{{\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{R}}}} \right)}^2}} \end{array}} \right]}\\ {\mathop {{W_\theta }}\limits_{3 \times 1} = \left[ {\begin{array}{*{20}{c}} {{{\left( {{\mathit{\boldsymbol{V}}^{\rm{G}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{G}}}{\mathit{\boldsymbol{V}}^{\rm{G}}}}&{{{\left( {{\mathit{\boldsymbol{V}}^{\rm{C}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{C}}}{\mathit{\boldsymbol{V}}^{\rm{C}}}}&{{{\left( {{\mathit{\boldsymbol{V}}^{\rm{R}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{R}}}{\mathit{\boldsymbol{V}}^{\rm{R}}}} \end{array}} \right]} \end{array} $ | (7) |
其中,
| $ \mathit{\boldsymbol{P}}_{k + 1}^i = \mathit{\boldsymbol{P}}_k^i \cdot c/\hat \sigma _{0,i}^2\quad (i = {\rm{G}},{\rm{C}},{\rm{R}}) $ | (8) |
式中,k为观测历元,c为任意常数,一般是选取
在非组合模型定位中,为尽可能精确估计斜向电离层延迟,采用欧洲定轨中心(CODE)提供的全球电离层模型(GIM)进行先验信息的约束,它具有几个TECu的精度。从GIM获得的垂直方向总电子含量(VTEC)导出斜路径总电子含量的虚拟观测方程为:
| $ \begin{array}{*{20}{c}} {\tilde I_{{\rm{r}},f}^{\rm{s}} = 40.28 \cdot {\rm{VTEC}}/\left( {f_f^2\cos \left( {{Z_\theta }} \right)} \right) + \varepsilon }\\ {\varepsilon \sim N\left( {0,\sigma _\varepsilon ^2} \right)} \end{array} $ | (9) |
先验方差为[12]:
| $ \sigma _\varepsilon ^2 = \left\{ \begin{array}{l} \sigma _{I,0}^2/{\sin ^2}\left( E \right),t < 8\;或\;t > 20\;或\;B > {60^{}}\\ \left( {\sigma _{I,0}^2 + \sigma _{I,1}^2\cos \left( B \right)\cos \left( {\frac{{t - 14}}{{12}}{\rm{ \mathsf{ π} }}} \right)} \right)/{\sin ^2}\left( E \right) \end{array} \right. $ | (10) |
式中, VTEC和Zθ分别为从GIM获得的垂直方向的总电子含量[13]和穿刺点(IPP)的天顶角;ε为GIM模型的误差;E和B分别为卫星高度角和穿刺点的大地纬度;t为IPP的当地时间;
斜向电离层变化的状态方程可以描述为:
| $ I_{i,{\rm{r}},f}^{\rm{s}} = I_{i - 1,{\rm{r}},f}^{\rm{s}} + \omega ,\omega \sim \left( {0,\sigma _\omega ^2} \right) $ | (11) |
式中,σω2为斜向电离层变化的先验方差,i为历元。因为斜向电离层延迟的变化速率与卫星高度角密切相关,本文采用式(6)求得斜向电离层延迟变化的先验方差:
| $ \sigma _\omega ^2 = \left\{ \begin{array}{l} \sigma _{{\omega _0}}^2,E \ge {30^ \circ }\\ \sigma _{{\omega _0}}^2/\left( {2\sin \left( E \right)} \right),E < {30^ \circ } \end{array} \right. $ | (12) |
式中,斜向电离层变化的先验方差
为削弱接收机DCB对组合PPP观测方程的影响,将其作为随机游走过程的参数进行估计:
| $ d_{i,{\rm{r}},f}^{\rm{s}} = d_{{\rm{i}} - 1,r,{\rm{f}}}^{\rm{s}} + \zeta ,\zeta \sim {\rm{N}}\left( {0,\sigma _{^\zeta }^2} \right) $ | (13) |
式中,ζ为接收机硬件延迟的白噪声,先验方差为
对多系统PPP来说,由于各系统信号结构和频率不同,接收机硬件延迟并不一致[11]。以GPS接收机的硬件延迟为基准值,BDS、GLONASS和GPS之间的接收机硬件延迟为系统间偏差(ISB),估计3个独立的接收机钟差。另外,由于GLONASS采用频分多址(FDMA)技术,因此每个GLONASS卫星的接收机硬件时延也有所不同,每2个GLONASS频率之间的差异称为内部频率偏差(IFB)。关于IFB的估计,我们估计2+nR个独立DCB参数,其中nR为每个历元可观测的GLONASS卫星数目。
1.2.3 其他策略采用无电离层组合模型和非组合模型分别解算,参数估计方法采用扩展的卡尔曼滤波(EKF)。对于无电离层组合模型,待估参数为接收机位置、接收机钟差、天顶对流层延迟的湿分量和无电离层组合的模糊度;对于非组合模型,待估参数为接收机位置、接收机钟差、天顶对流层延迟的湿分量、接收机DCB、内部频率偏差(IFB)、斜向电离层延迟和每个频率上的浮点模糊度。精密星历和精密钟差采用德国地学中心(GFZ)的产品,对流层延迟采用Saastamoinen(SAAS)对流层模型和全球投影函数(GMF)进行改正,对流层残差采用随机游走进行估计,天线参数、地球自转参数和DCB文件从IGS获得。除这些误差外,还进行了固体潮、海潮及极潮的修正。
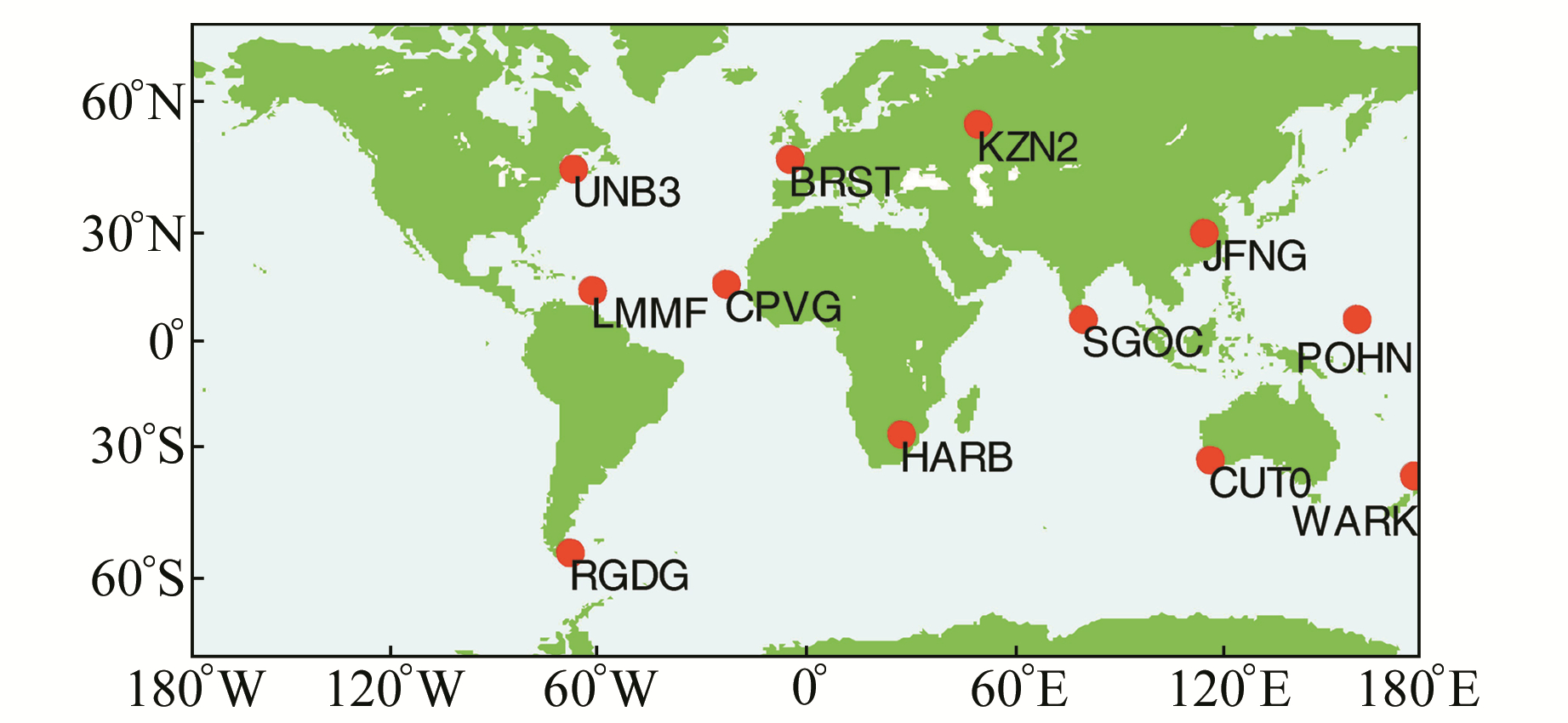
2 结果比较与分析 2.1 数据来源实验数据选取全球多系统定位服务实验网(MGEX)12个测站2015-05-01~05-07共7 d的观测数据,测站分布如图 1,采样间隔为30 s,分别解算静态和动态精密单点定位浮点解。
|
图 1 MGEX部分测站的分布 Fig. 1 The part of MGEX station distribution |
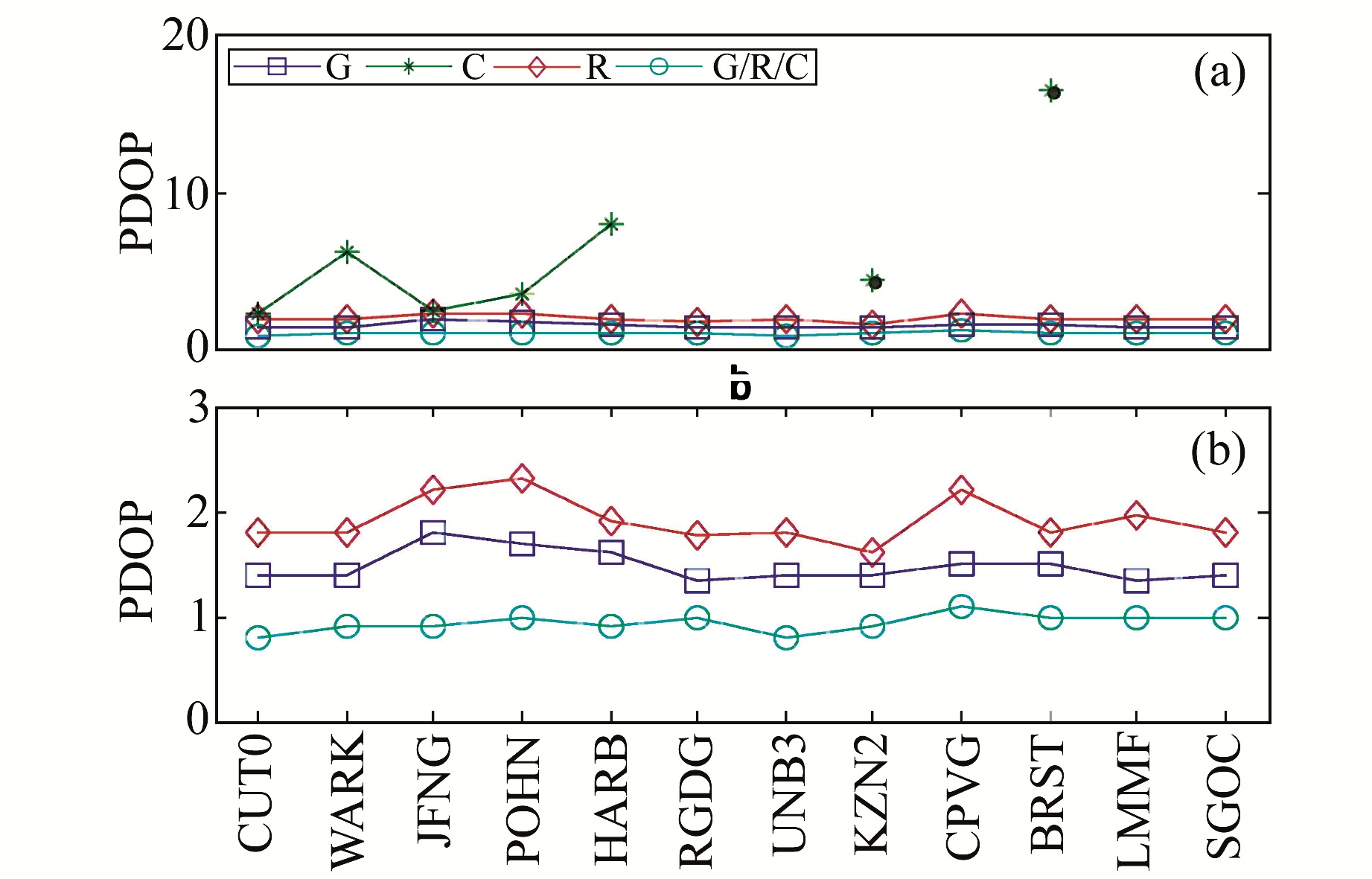
图 2和图 3是年积日为121的12个测站各系统全天可见卫星数和PDOP的平均值,其中各测站卫星截止高度角设置为5°,PDOP截止值设置为20。图 2中部分测站没有对应的BDS卫星数,表示当天观测到的卫星数较少且观测时段较短,进而在图 3中没有该测站对应BDS的PDOP值。图 2和图 3显示,GPS平均卫星数和平均PDOP值在不同测站之间变化幅度不大,且变化非常平稳;GLONASS平均卫星数相比GPS少2~3颗,平均PDOP值比GPS大0.4,变化也比较平稳;相比之下,BDS平均可见卫星数和平均PDOP值变化幅度较大,且位于西半球的测站如LMMF在某个时段利用单BDS系统不能进行单历元定位。对图 2和图 3中的数据进行统计,GPS、BDS、GLONASS平均卫星个数分别为10.5、5.0、8.13,3系统组合平均卫星数达到28.29;GPS、BDS、GLONASS平均PDOP值分别为1.48、6.15、1.91,3系统组合平均PDOP值为0.94。从12个测站统计结果可以看出,组合系统平均可见卫星数达28颗,PDOP值达0.94,虽然对于单GPS系统可以进行定位,但多个系统组合可明显增加可用卫星数,改善卫星几何构型,提高了解算结果的稳定性和可靠性。

|
图 2 测站平均可见卫星数 Fig. 2 The average satellite numbers of the stations |
|
图 3 测站平均PDOP值 Fig. 3 The average PDOP values of the stations |
在进行数据处理时,除采用的函数模型不同外,其他的数据处理策略完全相同。下面对2个函数模型3系统组合PPP从定位精度和收敛速度2个方面进行比较。
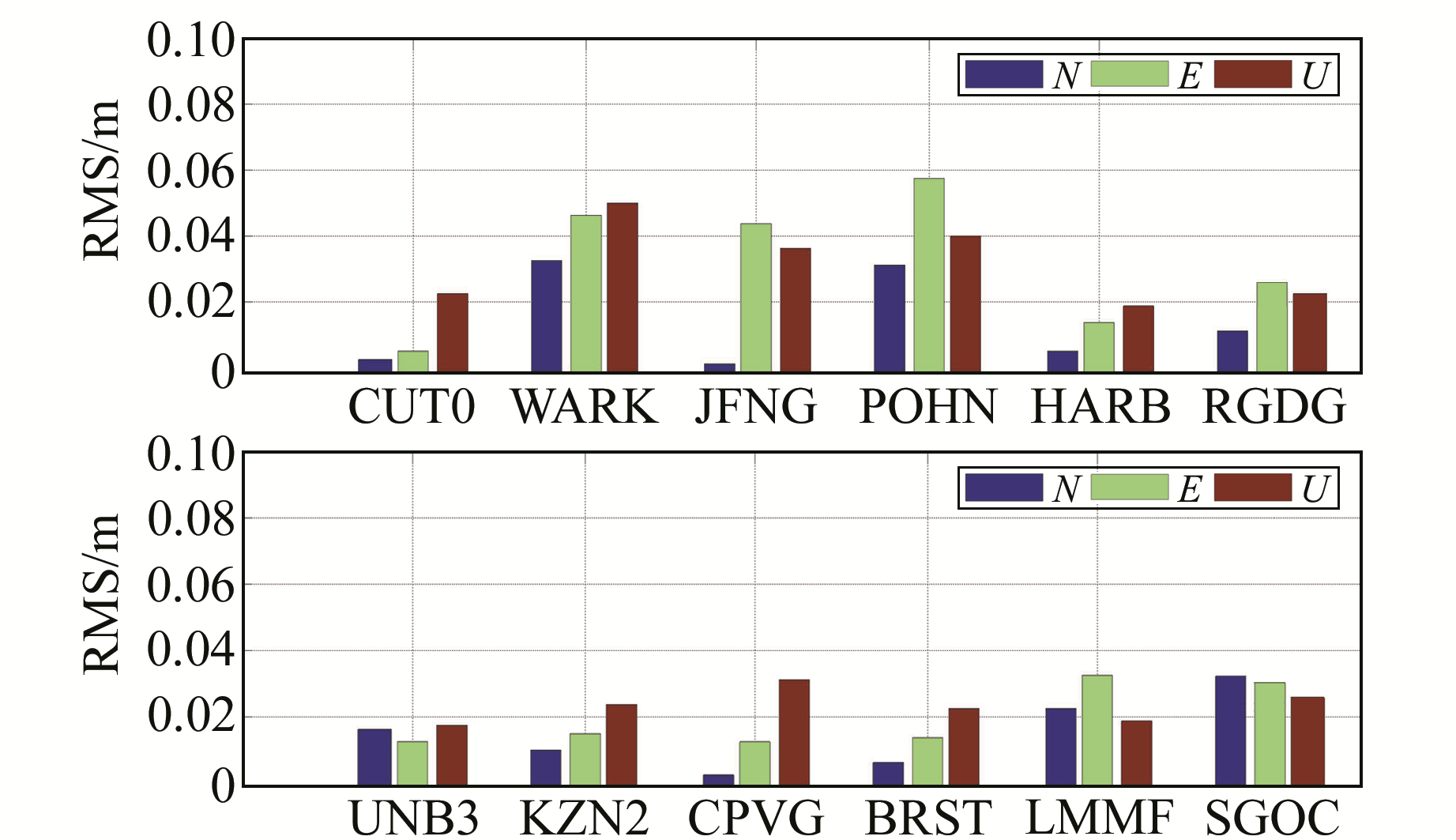
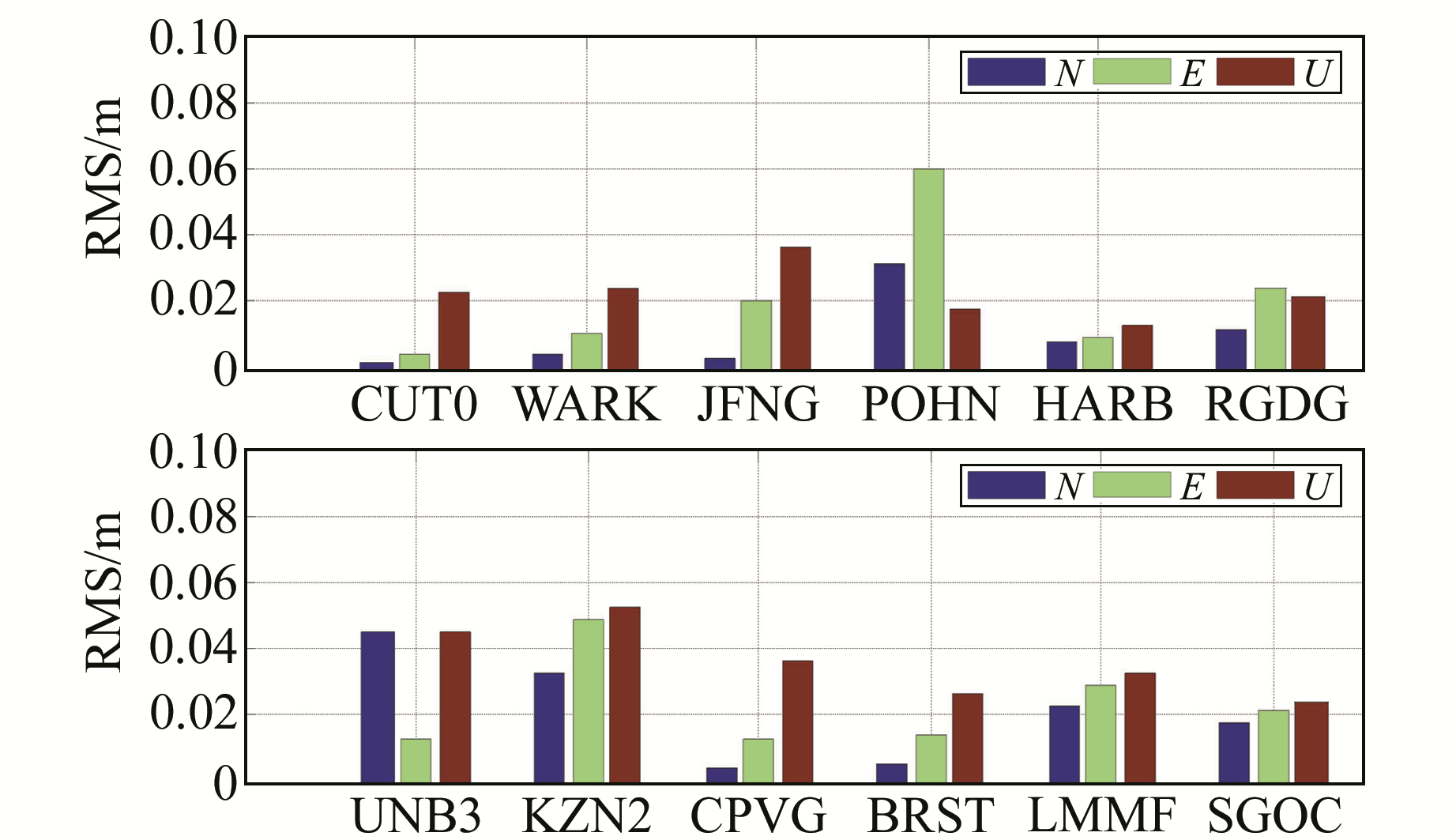
图 4和图 5分别为12个测站2种函数模型年积日为121的静态解算结果,其中把IGS提供的SINEX文件中的坐标作为参考值。由图可知,对于PPP单天解,除POHN测站外,RMS值都在3~5 cm;对所有测站2种函数模型的解算结果进行统计,无电离层函数模型在N、E、U 3个方向的平均RMS值分别为1.4 cm、2.5 cm、2.9 cm,非组合函数模型解算结果在N、E、U方向的RMS值分别为1.5 cm、2.4 cm、3.0 cm,2种函数模型的解算结果具有一致性。为了精确表达二者的差值,图 6给出了12个测站2种函数模型1周平均RMS值的差值图,对图中所有测站进行统计,2种函数模型在N、E、U 3个方向的平均RMS分别为1.8 mm、2.5 mm、2.9 mm。在cm级的精度要求下,可以认为2种函数模型在定位精度方面相当。
|
图 4 无电离层函数模型的RMS值 Fig. 4 Deviations from ionospheric model |
|
图 5 非组合函数模型的RMS Fig. 5 Deviation of non-combined model |

|
图 6 2种函数模型RMS的差值 Fig. 6 The difference between the two function models |
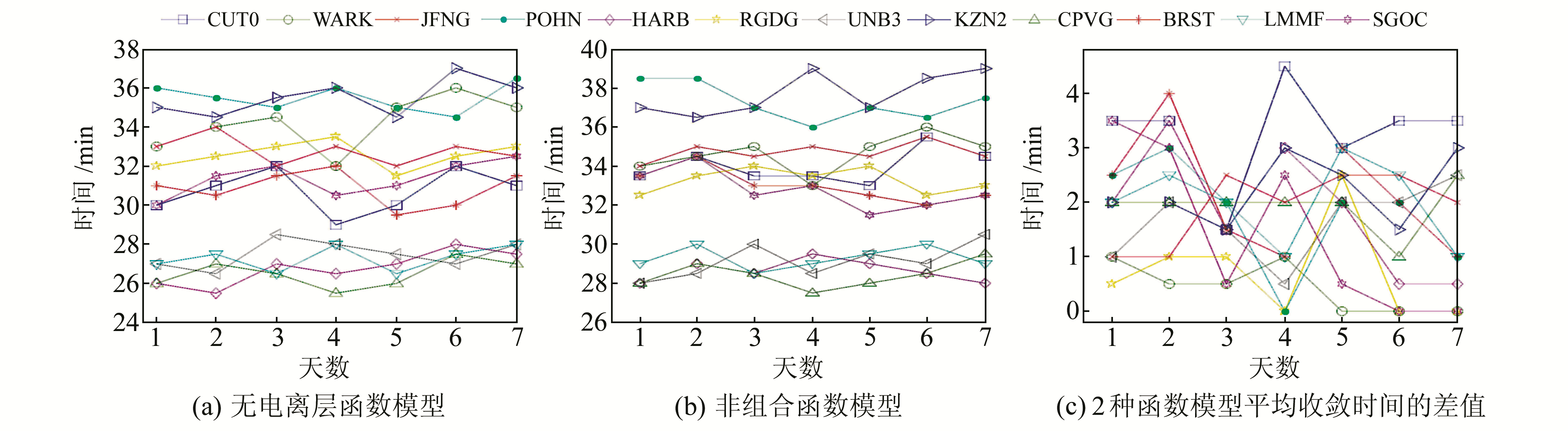
图 7(a)和图 7(b)统计了2种函数模型12个测站1周的收敛时间。在本文中,滤波收敛定义为N、E、U各方向定位偏差均小于10 cm。为确保结果可靠,只有当连续20个历元定位偏差均小于限值时,才认为该历元收敛[15]。由图可知,对于同一测站,各天之间收敛时间具有较好的一致性。由图 7(a)可知,无电离层组合函数模型解算的收敛时间分布在25~37 min,平均收敛时间为31.5 min;由图 7(b)可知,非组合函数模型解算的收敛时间分布在27~39 min,平均收敛时间为33 min,2种函数模型收敛时间相差不大。图 7(c)给出2种函数模型平均收敛时间的差值,差值均小于5 min,平均差值为2.2 min,可以认为2种函数模型的收敛速度也相当。
|
图 7 2种函数模型的收敛时间及其差值 Fig. 7 Convergence time of two ionospheric models and differences between them |
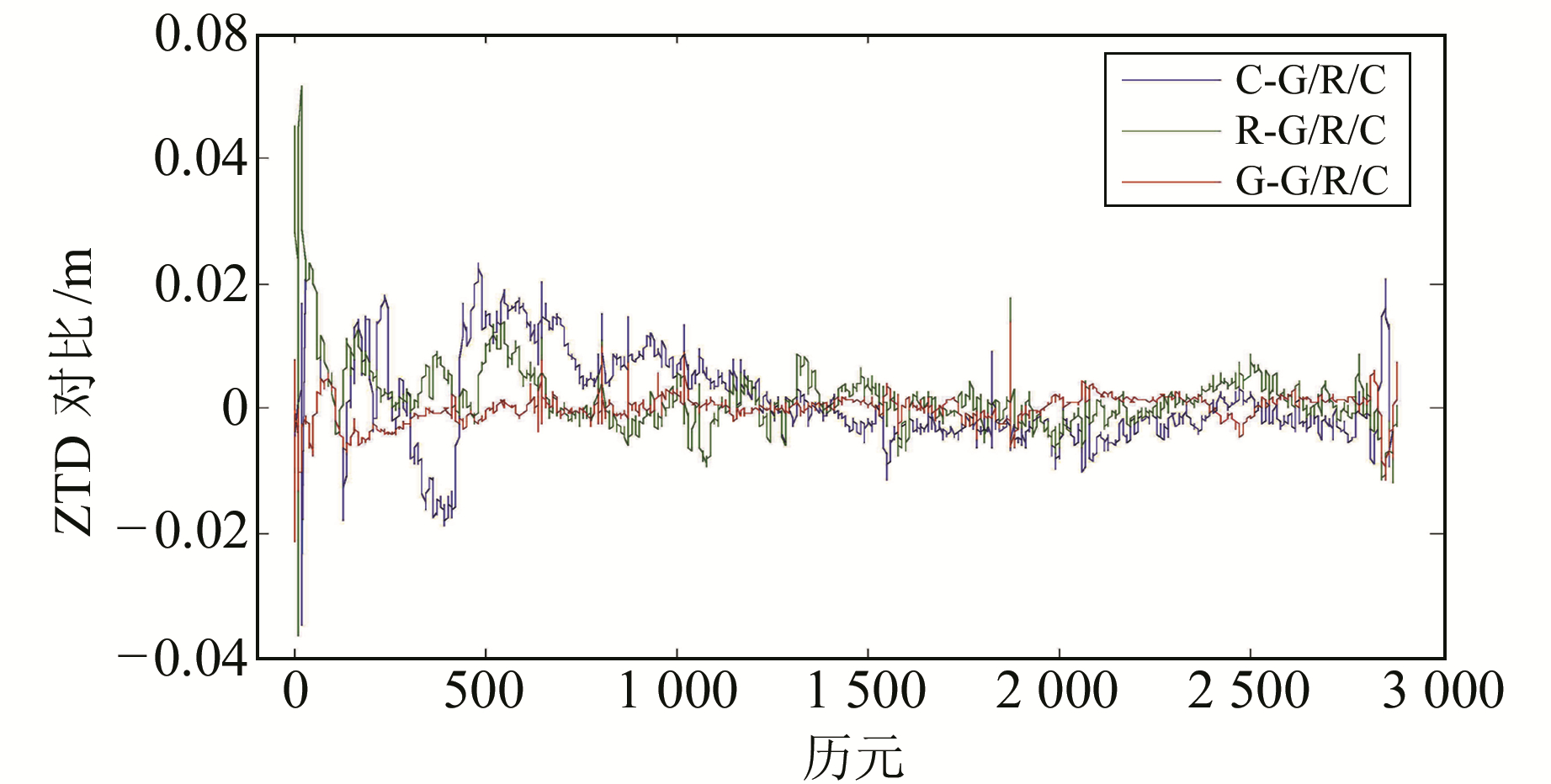
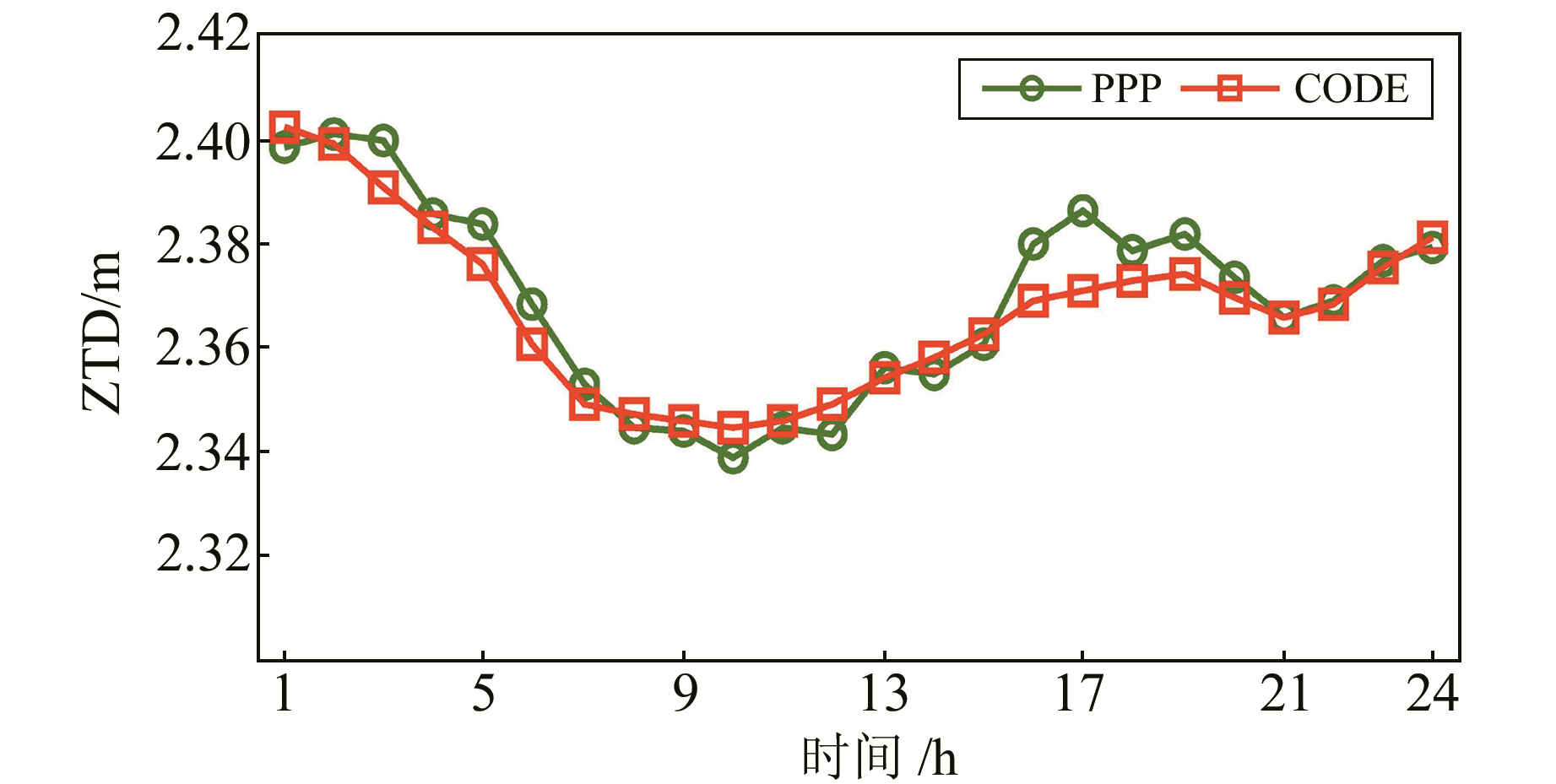
图 8为JFNG测站年积日为121的不同系统计算的天顶对流层延迟量差值对比图。由图可知,不同系统计算的天顶对流层延迟量的差值在收敛之后趋于一致。为更好地比较解算结果的准确性,图 9给出与CODE解算结果的对比,吻合程度较好,平均偏差为1.21 mm。为更全面地考察解算精度,图 10给出7 d ZTD解算结果与CODE偏差的平均值和RMS值。由图可知,平均偏差和RMS都在3 mm左右,经统计12个测站偏差平均值为1.59 mm,偏差RMS值为2.89 mm。
|
图 8 JFNG测站不同系统解算ZTD差值的对比 Fig. 8 Comparison of ZTD differences calculated by different systems at JFNG station |
|
图 9 JFNG测站ZTD与CODE的对比 Fig. 9 The ZTD of JFNG station compared with CODE |

|
图 10 ZTD偏差 Fig. 10 ZTD deviations |
为了比较单系统与多系统在动态定位中的差异,图 11给出单系统和多系统在不同高度角下的定位结果。由图可知,当高度角为10°时,单系统和多系统的定位结果相当,但多系统收敛速度更快,数据波动更小;当高度角为40°时,单系统解算的结果很不稳定,多系统此时表现出优越性,仍能得到可靠的解算结果。由此可知,高度角太大对单系统影响较大,对多系统影响较小。当截止高度角从10°增加到40°时,GPS可视卫星数有时减少到5颗以下,而多系统平均卫星数保持在10颗左右,这就是多系统能提供更加稳定的解算结果的原因。

|
图 11 CUT0测站不同高度角下PPP定位精度及可见卫星数 Fig. 11 Comparision of PPP results under different cut-off elevation angles at station CUT0 and the corresponding satellite numbers |
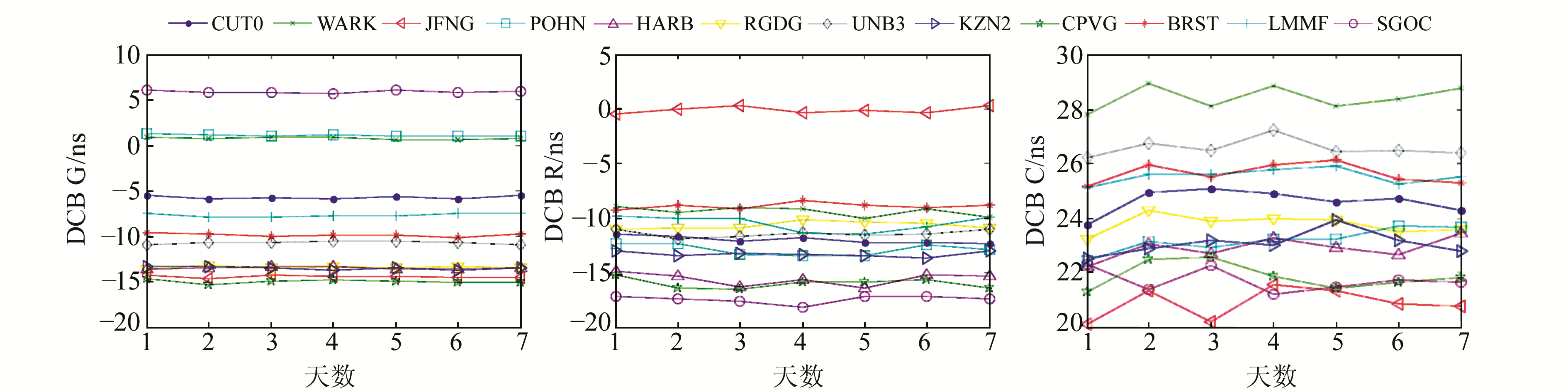
在进行非组合PPP解算时,接收机DCB作为参数同其他未知参数一并进行解算,图 12给出不同系统7 d解算的接收机DCB值。由图可知,对于GPS系统,每个测站的DCB值都比较稳定,绝对量级小于20 ns。将12个测站1周的解算结果同IGS作对比,所有测站平均偏差为0.15 ns;对于GLONASS系统,测站DCB值的稳定性低于GPS,所有测站同IGS平均偏差为0.32 ns;对于BDS系统,由于测距码的噪声比较大,DCB变化幅度较大,所有测站同IGS平均偏差较大,为0.54 ns。
|
图 12 不同系统接收机DCB在7 d的变化 Fig. 12 The weekly time series of receiver's DCB for different system |
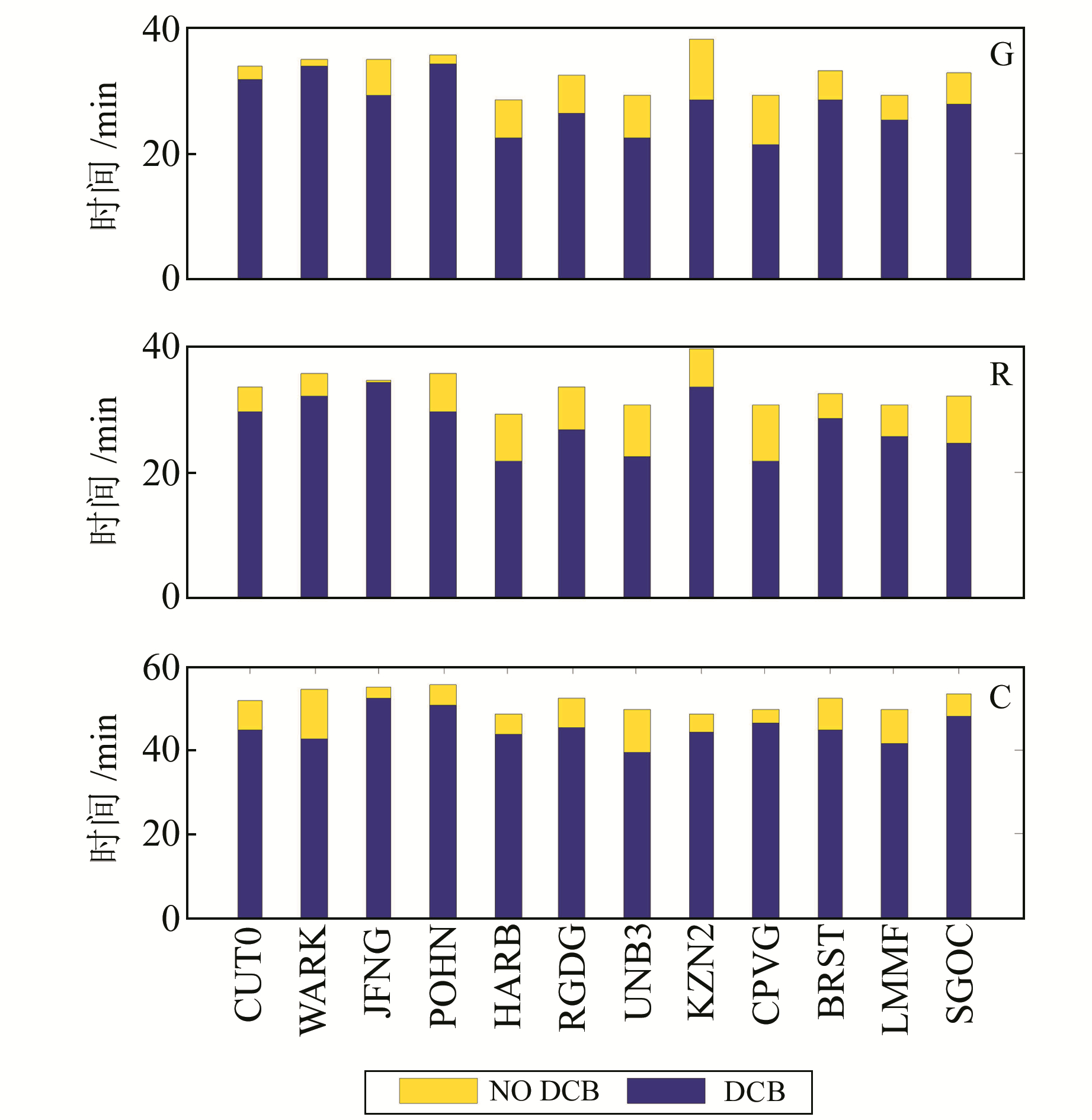
本文还研究了接收机DCB值的大小对PPP收敛时间的影响。图 13给出12个测站年积日为121的收敛时间统计图,由图可知,DCB值的大小对不同系统收敛速度的影响是不一样的。对于GPS系统,测站CPVG的DCB量级最大,收敛速度提高了11 min;对于GLONASS系统,测站SGOC收敛速度提高了9 min;对于BDS系统,测站WARK收敛速度提高了10 min。对3个系统的解算结果进行统计,在估计接收机DCB时收敛时间平均提高15%。
|
图 13 不同DCB值对收敛时间的影响 Fig. 13 The convergence time for different DCB |
本文比较了3系统组合精密单点定位的解算方法,从2个方面比较了PPP的函数模型:无电离层组合模型和非组合模型。在非组合模型中,采用电离层约束信息对电离层参数进行先验约束,并将接收机DCB当作参数一并解算,讨论对流层参数和DCB参数的解算结果,得出以下结论:
1) 多系统组合PPP对坐标、接收机DCB和对流层延迟等解算方案影响不大,但它极大地减小了PDOP值和收敛时间,对PPP的应用有实用价值;
2) 非组合模型收敛速度受接收机DCB的影响,不同量级的DCB值对收敛速度的影响不同,DCB值平均收敛时间提高15%;
3) 无电离层组合模型和非组合模型在5 cm的定位精度下可以认为是相当的;
4) 采用PPP解算的测站天顶方向的对流层延迟与CODE的平均偏差和RMS都在3 mm以内。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 005-5 017 DOI:10.1029/96JB03860
(  0) 0) |
| [2] |
Héroux P, Kouba J. GPS Precise Point Positioning Using IGS Orbit Products[J]. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 2001, 26(6): 573-578
(  0) 0) |
| [3] |
Azúa B M, DeMets C, Masterlark T. Strong Interseismic Coupling, Fault Afterslip, and Viscoelastic Flow before and after the Oct. 9, 1995 Colima-Jalisco Earthquake: Continuous GPS Measurements from Colima, Mexico[J]. Geophysical Research Letters, 2002, 29(8): 122
(  0) 0) |
| [4] |
Kubo N, Yasuda A, Kawano I, et al. The Benefits of Three Frequencies for the High Accuracy Positioning[C]. European Navigation Conference 2006, Manchester, 2006
(  0) 0) |
| [5] |
Ren X D, Zhang K K, Li X X, et al. Precise Point Positioning with Multi- Constellation Satellite Systems:Beidou, Galileo, GLONASS, GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1 307-1 313
(  0) 0) |
| [6] |
Cai C S, Gao Y. Precise Point Positioning Using Combined GPS and GLONASS Observations[J]. Journal of Global Positioning Systems, 2007, 6(1): 13-22 DOI:10.5081/jgps
(  0) 0) |
| [7] |
Jokinen A, Feng S J, Milner C, et al. Precise Point Positioning and Integrity Monitoring with GPS and GLONASS[C]. European Navigation Conference 2011, London, 2011
(  0) 0) |
| [8] |
Zhang H P, Gao Z Z, Ge M R, et al. On the Convergence of Ionospheric Constrained Precise Point Positioning (IC-PPP) Based on Undifferential Uncombined Raw GNSS Observations[J]. Sensors, 2013, 13(11): 15 708-15 725 DOI:10.3390/s131115708
(  0) 0) |
| [9] |
Tu R, Ge M R, Zhang H P, et al. The Realization and Convergence Analysis of Combined PPP Based on Raw Observation[J]. Advances in Space Research, 2013, 52(1): 211-221 DOI:10.1016/j.asr.2013.03.005
(  0) 0) |
| [10] |
Ge Y L, Zhou F, Sun B Q, et al. The Impact of Satellite Time Group Delay and Inter-Frequency Differential Code Bias Corrections on Multi-GNSS Combined Positioning[J]. Sensors, 2017, 17(3): 602
(  0) 0) |
| [11] |
Li X X, Ge M R, Dai X L, et al. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, Beidou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635 DOI:10.1007/s00190-015-0802-8
(  0) 0) |
| [12] |
Gao Z Z, Ge M R, Shen W B, et al. Ionospheric and Receiver DCB-Constrained Multi-GNSS Single-Frequency PPP Integrated with MEMS Inertial Measurements[J]. Journal of Geodesy, 2017, 91(8): 1 351-1 366
(  0) 0) |
| [13] |
Schaer S, Gurtner W, Feltens J. IONEX: The Ionosphere Map Exchange Format Version 1[C]. IGS AC Workshop, Darmstadt, 1998
(  0) 0) |
| [14] |
Gao Z Z, Zhang H P, Ge M R, et al. Tightly Coupled Integration of Ionosphere-Constrained Precise Point Positioning and Inertial Navigation Systems[J]. Sensors, 2015, 15(3): 5 783-5 802 DOI:10.3390/s150305783
(  0) 0) |
| [15] |
Li P, Zhang X. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J]. GPS Solutions, 2014, 18(3): 461-471 DOI:10.1007/s10291-013-0345-5
(  0) 0) |
2. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, 999 Xi'an Road, Chengdu 611756, China;
3. National Time Service Center, CAS, 3 East-Shuyuan Road, Xi'an 710600, China
 2019, Vol. 39
2019, Vol. 39

