研究表明,GPS坐标时间序列(特别是高程方向)由于存在显著的季节性变化[1-2]而影响精度的进一步提高。季节性信号的提取方法有最小二乘拟合法[3]和奇异谱分析法(SSA)[4-6],前者通常会将季节性信号作为规则的正余弦函数进行处理,与实际情况不符,难以准确提取周期信号;后者则是从时间序列的动力结构出发,因可以根据其自身特性稳定识别和强化周期信号[7]而广泛应用。
多道奇异谱分析法(multichannel singular spectrum analysis,MSSA)是在SSA基础上发展而来的,常用于有用信息的提取和重构去噪。目前关于MSSA的研究并不多,Oropeza[8]利用MSSA重建叠前不规则3D数据并去噪;Zotov[9]将MSSA应用于大气角动量的质量和运动相关研究;魏小强[10]提出基于MSSA的地震三维数据规则化方法。本文基于MSSA对GPS站点季节性信号进行提取,同时考虑空间和时间相关性,能更好地从GPS原始高程时间序列中去除单个站点的特有噪声并提取多个站点具有共性的季节性信号。
1 多通道奇异谱分析MSSA的研究对象为多维中心化时间序列xi(l),上标l表示通道序号,下标i为时间序号,l=0, 1, 2, …, L,i=0, 1, 2, …, N。分别将第l通道时间序列xi(l)按照嵌入维数M、时滞1排列成M行、N-M+1列的时滞矩阵,则:
| $ \mathit{\boldsymbol{X}}{\rm{ }} = \left[ {\begin{array}{*{20}{c}} {{\rm{ }}x_1^{\left( 1 \right)}}&{x_2^{\left( 1 \right)}}&{ \ldots {\rm{ }}}&{x_{i + 1}^{\left( 1 \right)}}&{ \ldots {\rm{ }}}&{{\rm{ }}x_{N - M + 1}^{\left( 1 \right)}}\\ \vdots &{ \vdots }& \ddots &{ \vdots }& \ddots &{ \vdots }\\ {x_M^{\left( 1 \right)}}&{x_{M + 1}^{\left( 1 \right)}}&{ \ldots {\rm{ }}}&{x_{i + M}^{\left( 1 \right)}}&{ \ldots {\rm{ }}}&{x_N^{\left( 1 \right)}}\\ {x_1^{\left( 2 \right)}}&{x_2^{\left( 2 \right)}}&{ \ldots {\rm{ }}}&{x_{i + 1}^{\left( 2 \right)}}&{ \ldots {\rm{ }}}&{x_{N - M + 1}^{\left( 2 \right)}}\\ { \vdots }&{ \vdots }& \ddots &{ \vdots }& \ddots &{ \vdots }\\ {x_M^{\left( 2 \right)}}&{x_{M + 1}^{\left( 2 \right)}}&{ \ldots {\rm{ }}}&{x_{i + M}^{\left( 2 \right)}}&{ \ldots {\rm{ }}}&{x_N^{\left( 2 \right)}}\\ { \vdots }&{ \vdots }& \ddots &{ \vdots }& \ddots &{ \vdots }\\ {x_1^{\left( L \right)}}&{x_2^{\left( L \right)}}&{ \ldots {\rm{ }}}&{x_{i + 1}^{\left( L \right)}}&{ \ldots {\rm{ }}}&{x_{N - M + 1}^{\left( L \right)}}\\ { \vdots }&{ \vdots }& \ddots &{ \vdots }& \ddots &{ \vdots }\\ {x_M^{\left( L \right)}}&{x_{M + 1}^{\left( L \right)}}&{ \ldots {\rm{ }}}&{x_{i + M}^{\left( L \right)}}&{ \ldots {\rm{ }}}&{x_N^{\left( L \right)}} \end{array}} \right] $ | (1) |
由式(1)可知,X为L×M行、N-M+1列矩阵,则X的自协方差阵CX= XXT为L×M维分块Toeplitz矩阵[11]:
| $ \mathit{\boldsymbol{C}}{_X} = \left[ {\begin{array}{*{20}{c}} {{\rm{ }}\mathit{\boldsymbol{C}}{_{11}}}&{\mathit{\boldsymbol{C}}{_{12}}}&{ \ldots {\rm{ }}}&{\mathit{\boldsymbol{C}}{_{1L}}}\\ {\mathit{\boldsymbol{C}}{_{21}}}&{\mathit{\boldsymbol{C}}{_{22}}}&{ \ldots {\rm{ }}}&{\mathit{\boldsymbol{C}}{_{2L}}}\\ \vdots & \vdots & \ddots & \vdots \\ {\mathit{\boldsymbol{C}}{_{1L}}}&{\mathit{\boldsymbol{C}}{_{L2}}}&{ \ldots {\rm{ }}}&{\mathit{\boldsymbol{C}}{_{LL}}} \end{array}} \right] $ | (2) |
其中Cll′表示第l、l′两个通道时间序列之间的滞后协方差矩阵,其第j行j′列元素采用Yule-Walke估计其最优值为:
| $ {(\mathit{\boldsymbol{C}}{_{ll\prime }})_{j, j\prime }} = \frac{1}{{{\rm{ }}N - \left| {j - j\prime } \right|}}\sum\limits_{i = 1{\rm{ }}}^{N - \left| {j - j\prime } \right|} {} {\rm{ }}x_{i + j}^{(l)}x_{i + j - j\prime }^{(l\prime )} $ | (3) |
计算CX的特征值λk和特征向量Pk,满足CXPk=λkPk。将特征值最大值赋值给λ1,按降序排列可得λ1≥λ2≥…≥λLM≥0,则时间序列xi(l)的奇异谱为
计算式(1)中第i个状态向量Xi在特征向量Pk上的正交投影系数为:
| $ {a_{i, k}} = {\rm{ }}{\mathit{\boldsymbol{X}}_i}{\mathit{\boldsymbol{P}}_k} = \sum\limits_{l = 1}^L {} \sum\limits_{j = 1}^M {} x_{i + j}^{(l)}P_{j, k}^{(l)} $ | (4) |
式中,
重建成分(reconstructed components,RC)是MSSA中一项至关重要的步骤,关系到能否有效提取趋势周期项及去噪。RC由ST-EOF和ST-PC共同构成[12]:
| $\begin{array}{l} x_{i, k}^{(l)} = \\ \left\{ \begin{array}{l} \frac{1}{{i{\rm{ }}}}\sum\limits_{j = 1}^i {} {\rm{ }}{a_{i - j, k}}P_{j, k}^{(l)}, 1 \le i \le M - 1\\ \frac{1}{{M{\rm{ }}}}\sum\limits_{j = 1}^M {} {\rm{ }}{a_{i - j, k}}P_{j, k}^{(l)}, {\rm{ }}M \le i \le N - M + 1\\ \frac{1}{{N - i + 1}}\sum\limits_{j = i - N + M}^M {} {\rm{ }}{a_{i - j, k}}P_{j, k}^{(l)}, N - M + 2 \le i \le N \end{array} \right. \end{array} $ | (5) |
L×M个RC线性相加应与原始序列xi(l)相同。为了达到去除噪声的效果,可选取前K项重建成分RC重构原始序列主要信号:
| $ \hat x_i^{\left( l \right)} = \sum\limits_{k = 1}^K {} {\rm{ }}x_{j, k}^{(l)} $ | (6) |
显而易见,当L=1时,MSSA成为SSA。当原始序列中存在周期成分时,如果:1)自协方差CX的两个连续特征值λk、λk-1近似相等;2)各自对应的两个ST-EOF具有精确的频率并正交(如正/余弦函数sin(x)/cos(x));3)主成分ST-PC亦相互正交。那么,xi(l)的一个周期项就等于满足上述特性的两个相邻RC之和,据此可进一步提取GPS站点坐标时间序列中1 a项、0.5 a项等季节性信号。
2 实验与分析 2.1 实验数据实验采用的数据为CMONOC观测数据(ftp://ftp.cgps.ac.cn/products/position/),采样率为30 s, 利用GAMIT/GLOBK对数据进行后处理。选取时间跨度为2012-01~2016-12的GPS单天坐标时间序列,每个时间序列记录总数为1 824。选取CMONOC位于华北陆块的BJFS(房山)、TAIN(泰安)、JIXN(蓟县)及ZHNZ(郑州)4个监测站垂直方向的观测数据进行分析。由于数据中含有粗差并有数据缺失,先对其进行预处理[2]。采用四分位距法对数据中的粗差进行剔除,并利用三次多项式插值法对缺失项进行插补,进而获取高精度的连续时间序列。为了方便季节性变化信号的提取,利用最小二乘拟合法去除时间序列中的线性趋势项。
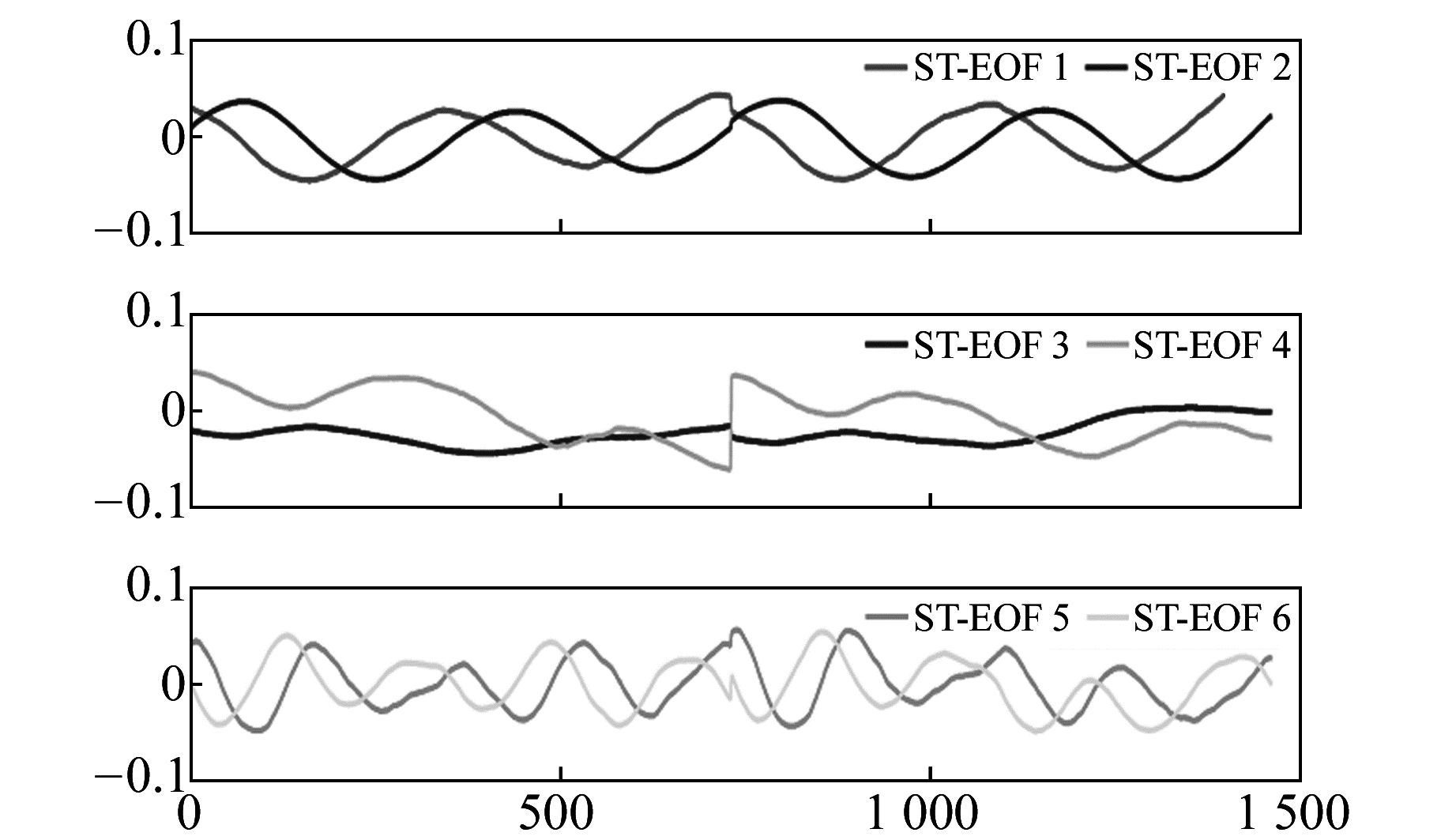
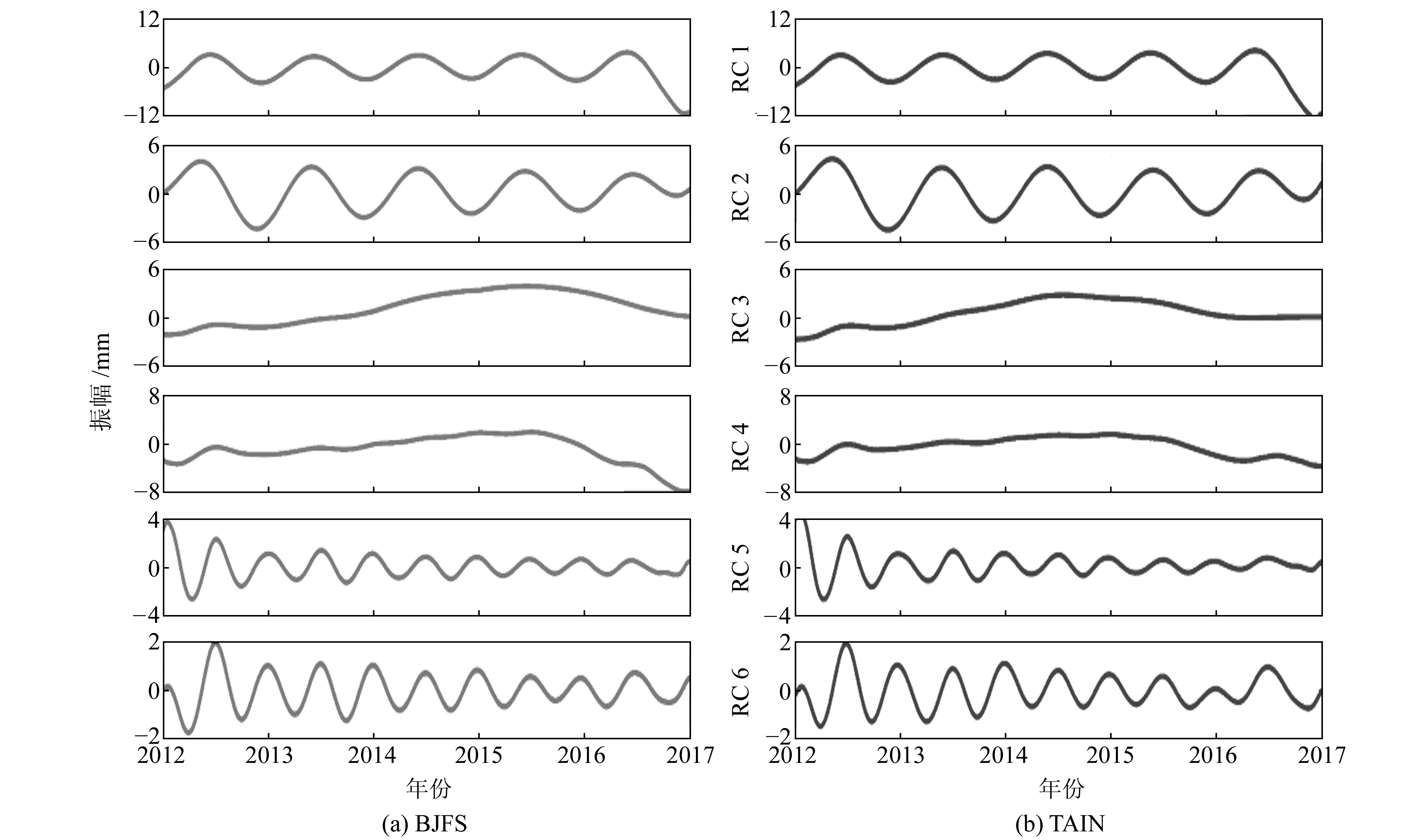
2.2 季节性信号提取采用MSSA提取BJFS、TAIN、JIXN及ZHNZ等4个监测站的季节性信号,应先计算出各自的重建成分。选取2 a时长为MSSA的嵌入维数,即M=730,图 1、图 2分别为BJFS与TAIN两站ST-EOF 1~6与重建成分RC 1~6的仿真结果。可以看出,ST-EOF 1~2、RC 1~2均呈现以1 a为周期的谐波振动,可以重构为1 a项;ST-EOF 3~4、RC 3~4无明显振动周期,构成长期非线性周期项的重建成分;两站ST-EOF 5~6仿真曲线虽有微小波动,但整体与RC 5~6曲线一致,均存在明显的振动周期,且为0.5 a,可重构为0.5 a项。同样,可依此方法判别JIXN与ZHNZ两站的1 a项与0.5 a项的组成成分。
|
图 1 BJFS与TAIN两站ST-EOF 1~6仿真结果 Fig. 1 Simulation results of BJFS and TAIN two stations ST-EOF 1~6 |
|
图 2 BJFS与TAIN两站重建成分RC 1~6的仿真结果 Fig. 2 Simulation results of BJFS and TAIN two stations reconstruction components RC 1~6 |
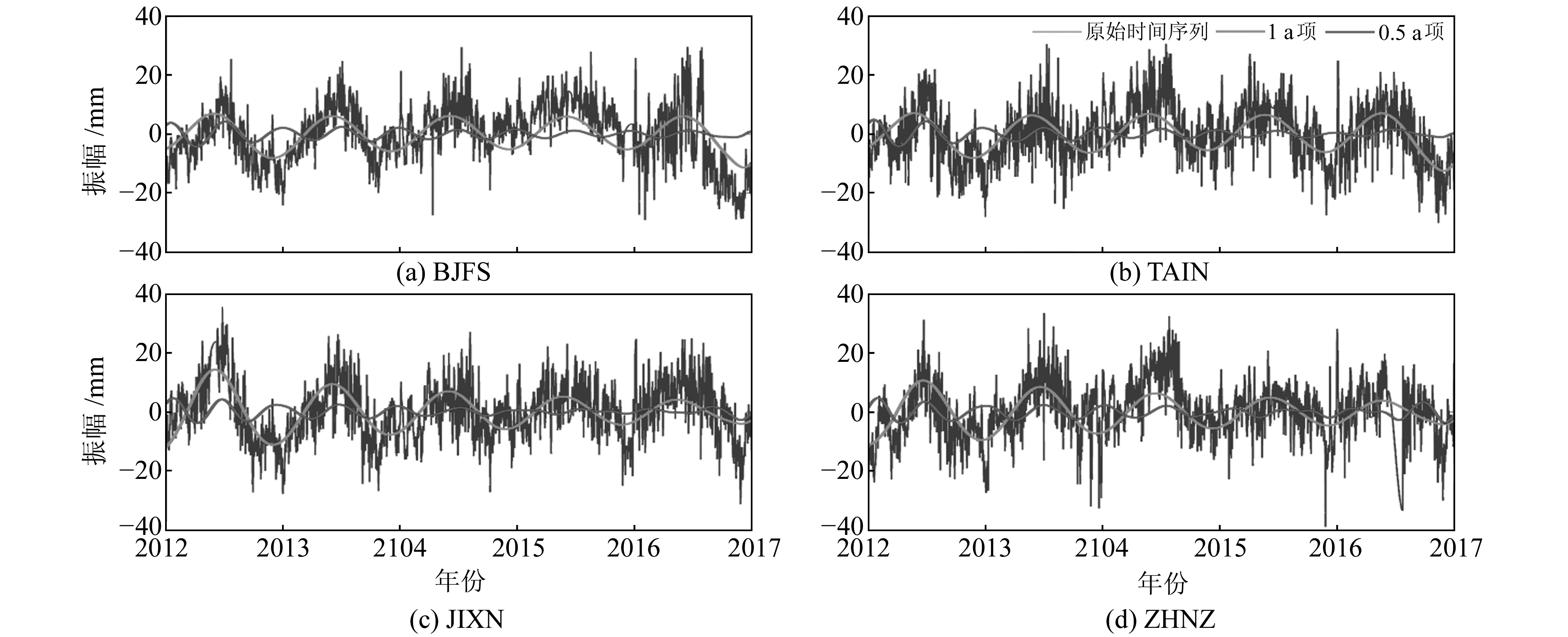
对所选4站的1 a项与0.5 a项进行提取,结果如图 3。可见,MSSA提取所选站点的季节性信号效果较优,周期信号振动稳定,且与原始数据吻合度较高。图 3(a)显示,BJFS站2015~2016年间1 a项略低于原始数据,而2016-06~2017年则略高。此现象可能是受站点当地特有现象影响,或是由其他非线性周期项引起[13]。由图 3(c)可知,JIXN站2015~2017年间0.5 a项信号较弱,但整体仍呈现以0.5 a为周期的谐波振动。
|
图 3 采用MSSA提取4个站点时间序列的1 a项和0.5 a项 Fig. 3 Use MSSA to extract annual and semi-annual items of four stations time series |
均方根误差(RMS)可作为衡量观测数据质量好坏的标准之一,RMS值越小,观测数据质量越好。计算可知,上述4个站点的原始数据RMS值大致相等,约为9.997;采用MSSA提取季节性信号后,RMS值依次为8.004、8.108、7.409、8.461,RMS值均有所降低。可见,采用MSSA提取GPS站点高程时间序列的季节性信号可进一步提高观测数据的质量。
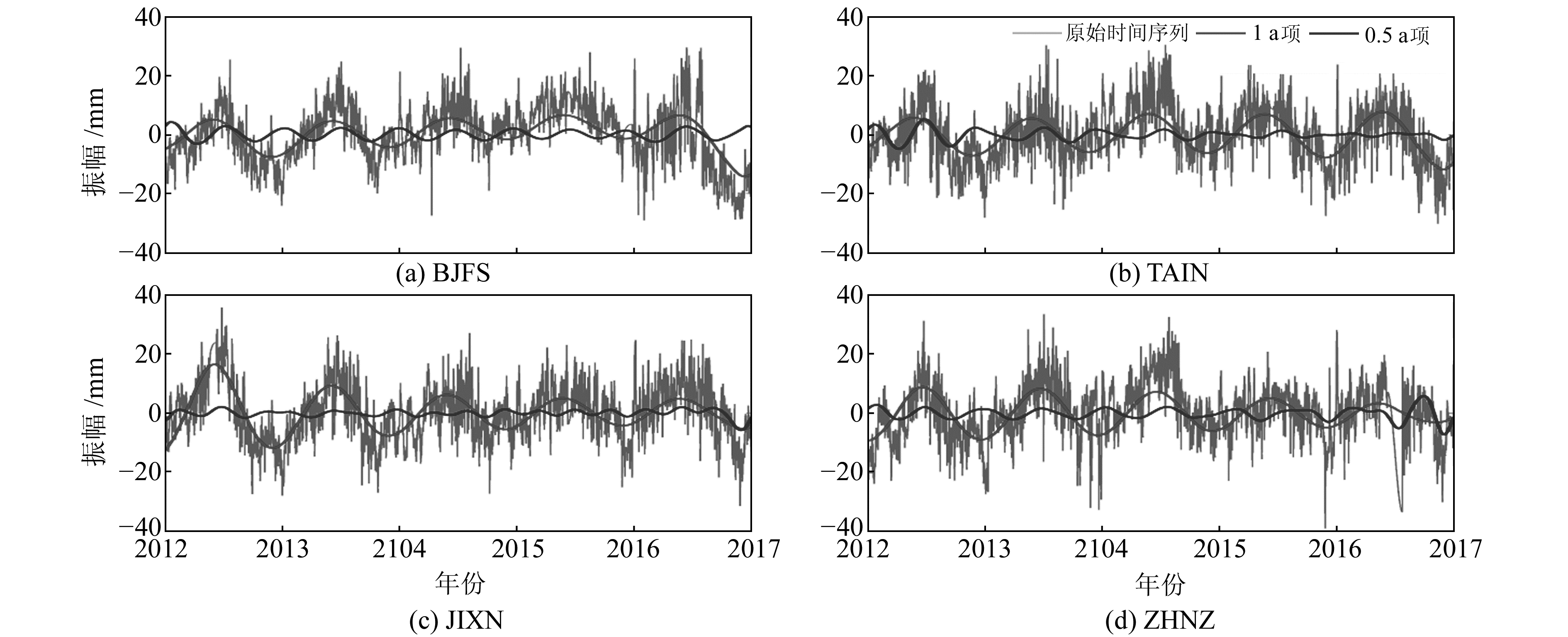
2.3 提取效果对比给出SSA提取上述4个站点季节性信号的结果,如图 4。将图 3与图 4对比可知,BJFS与ZHNZ两站结果基本一致,但图 4(b)显示,TAIN站2015~2017年间0.5 a项呈现无规则振动;图 4(c)显示,JIXN站2012~2014年间存在0.5 a项信号,而2014~2017年间呈现约0.3 a为周期的谐波振动,但构成周期项的重建成分一致。相比较SSA,MSSA由于考虑到区域GPS站点的时空相关性,能够更好地提取其坐标时间序列具有共性的1 a项与0.5 a项。
|
图 4 采用SSA提取4站时间序列的1 a项和0.5 a项 Fig. 4 Use SSA to extract annual and semi-annual items of four stations time series |
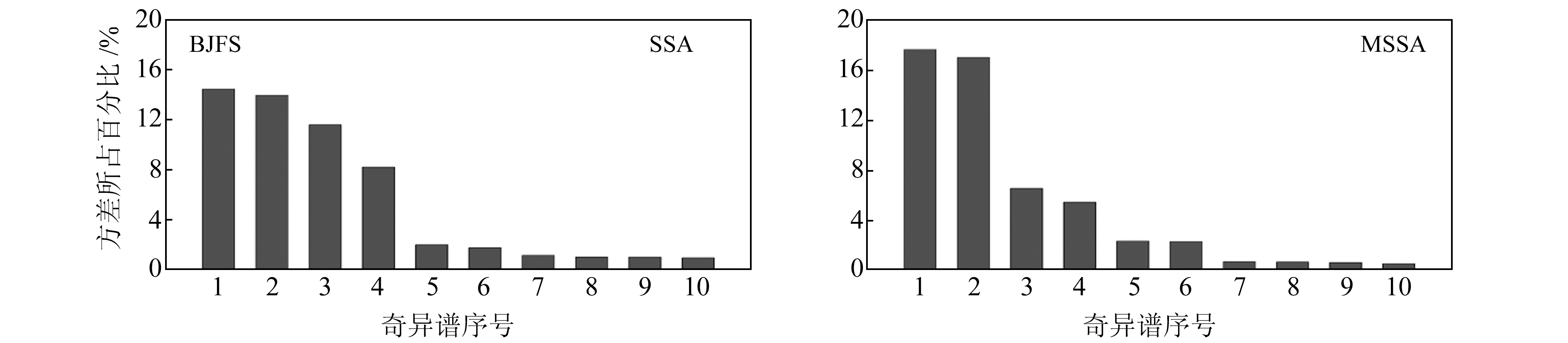
本文给出SSA与MSSA提取信号时各自的奇异谱方差所占百分比,如图 5所示(SSA单站提取BJFS站,MSSA共同提取BJFS等4站)。奇异谱1和奇异谱2对应的ST-EOF 1~2与ST-PC 1~2组成的重建成分RC 1~2可重构为1 a项。依次类推,奇异谱3、奇异谱4对应非线性周期项,奇异谱5、奇异谱6对应0.5 a项;奇异谱7~10则对应其他信号,但两者相差不大,在此不作考虑。图 5显示,MSSA提取1 a项的奇异谱方差占总体比重的35%,比SAA(28%)高7%,在一定程度上说明MSSA提取1 a项效果较SSA更佳,意味着利用SSA提取1 a项时容易受到干扰信号的影响,而采用MSSA处理时则受影响较小甚至不受影响。提取0.5 a项信号时,MSSA对应的奇异谱方差占总体比例为5%,比SSA(3.5%)高1.5%,即MSSA提取效果的优势依然存在,但并不明显。但对非线性周期项而言,MSSA奇异谱方差所占比例为12%,比SSA(18%)低6%,说明SAA较MSSA更适合提取长期非线性周期项。
|
图 5 SSA/MSSA提取季节信号时奇异谱方差所占百分比 Fig. 5 The percentage of singular spectral variance of seasonal signal extractionby SSA or MSSA |
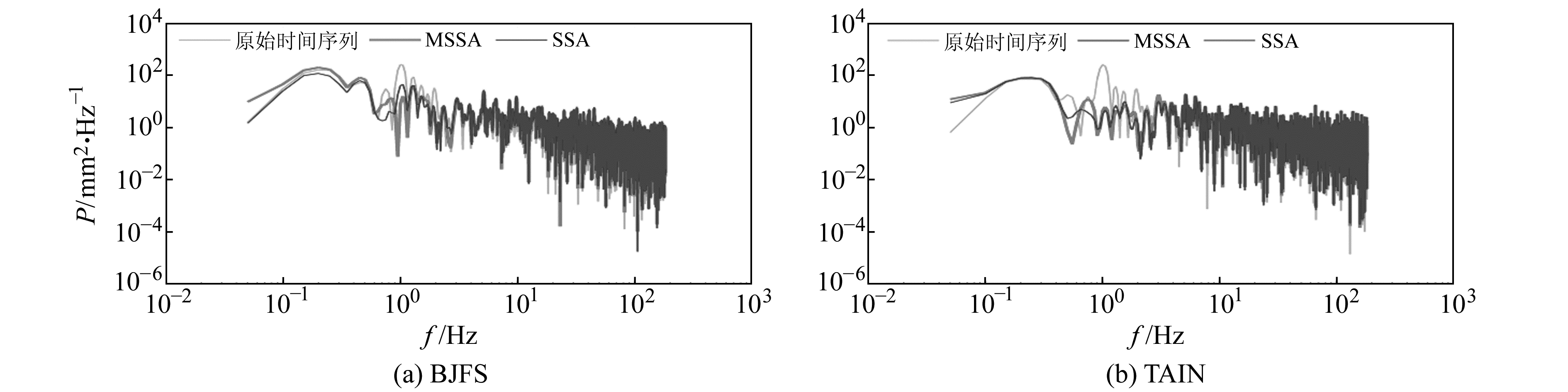
进一步选取SSA、MSSA处理站点时间序列时前10个重建成分重构信号进行对比。以BJFS与TAIN两站为例,由图 6(a)、图 6(b)看出,SSA曲线中含有较多的站点特有噪声,并受站点周边环境影响。具体表现为,BJFS站2014~2017年间、TAIN站2013~2015年间受噪声影响严重,SSA曲线均有明显波动。由图 6(c)、图 6(d)可见,MSSA曲线5 a内均较为平滑,体现了MSSA善于提取多个GPS站点时间序列中具有共性的信号,进而有效地消除了单个站点周边环境与特有噪声的影响。图 7显示BJFS和TAIN两站功率谱分析的结果,其中MSSA的低频整体比SSA高,是由于SSA只对每个时间序列进行周期项提取,因而不能很好地将周期项与其他信号、噪声分离,以致消除了更多周期项频率段对应的功率谱能量。综上,MSSA在提取季节性信号时较SSA存在一定优势。

|
图 6 SSA、MSSA处理BJFS与TAIN站点时间序列时前10个重建成分重构信号对比 Fig. 6 Comparison of the top ten reconstruction components reconstructed signals of BJFS and TAIN stations time series by SSA or MSSA |
|
图 7 BJFS与TAIN两站坐标时间序列功率谱分析 Fig. 7 Power spectrum analysis of BJFS and TAIN two stations coordinate time series |
本文基于MSSA同时提取多个GPS站点时间序列中1 a项与0.5 a项。通过与SSA对比可知,MSSA提取季节性信号时占绝对优势,但在识别长期非线性周期项时并无优势。考虑GPS站点信号同时受周边水文环境与自身特有噪声的影响而导致精度有所降低,文中采用MSSA与SSA前10个重建成分RC 1~RC 10进行信号重构。结果表明,MSSA能更有效地消除站点信号的特有噪声与其他影响,进而增强季节性信号的提取效果,通过功率谱分析也进一步验证了该观点。但是,嵌入维数M与重建成分的选取对MSSA分析结果的影响有待进一步研究。
| [1] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型的建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartograhica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [2] |
明峰, 杨元喜, 曾安敏, 等. 中国区域IGS站高程时间序列季节性信号及长期趋势分析[J]. 中国科学:地球科学, 2016, 46: 834-844 (Ming Feng, Yang Yuanxi, Zeng Anmin, et al. Analysis of Seasonal Signals and Long-Term Trends in the Height Time Series of IGS Sites in China[J]. Science China Earth Sciences, 2016, 46: 834-844)
(  0) 0) |
| [3] |
卢辰龙, 匡翠林, 戴吾蛟, 等. 采用变系数回归模型提取GPS坐标序列季节性信号[J]. 大地测量与地球动力学, 2014, 34(5): 94-100 (Lu Chenlong, Kuang Cuilin, Dai Wujiao, et al. Extracting Seasonal Signals from Continuous GPS Time Series Based on Varying-coefficient Regression Models[J]. Jouranl of Geodesy and Geodynamics, 2014, 34(5): 94-100)
(  0) 0) |
| [4] |
Chen Q, Dam T, Sneeuw N, et al. Singular Spectrum Analysis for Modeling Seasonal Signals from GPS Time Series[J]. Journal of Geodynamics, 2013(72): 25-35
(  0) 0) |
| [5] |
王解先, 连丽珍, 沈云中. 奇异谱分析在GPS站坐标监测时间序列分析中的应用[J]. 同济大学学报:自然科学版, 2013, 41(2): 282-288 (Wang Jiexian, Lian Lizhen, Shen Yunzhong. Application of Singular Spectrum Analysis to GPS Station Coordinate Monitoring Series[J]. Journal of Tongji University:Natural Science, 2013, 41(2): 282-288)
(  0) 0) |
| [6] |
罗勇, 匡翠林, 卢辰龙, 等. 基于SSA的GPS坐标序列去噪及季节性信号提取[J]. 大地测量与地球动力学, 2015, 35(3): 391-395 (Luo Yong, Kuang Cuilin, Lu Chenlong, et al. GPS Coordinate Series Denoising and Seasonal Signal Extraction Based on SSA[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 391-395)
(  0) 0) |
| [7] |
卢辰龙, 匡翠林, 易重海, 等. 奇异谱分析滤波法在消除GPS多路径中的应用[J]. 武汉大学学报:信息科学版, 2015, 40(7): 924-931 (Lu Chenlong, Kuang Cuilin, Yi Zhonghai, et al. Singular Spectrum Analysis Filter Method for Mitigation of GPS Multipath Errors[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 924-931)
(  0) 0) |
| [8] |
Oropeza V, Sacchi M. Simultaneous Seismic Data Denoising and Reconstruction via Multichannel Singular Spectrum Analysis[J]. Geophysics, 2011, 76(3): 25-32 DOI:10.1190/1.3552706
(  0) 0) |
| [9] |
Zotov L, Sidorenkov N S, Bizouard C, et al. Multichannel Singular Spectrum Analysis of the Axial Atmospheric Angular Momentum[J]. Geodesy and Geodynamics, 2017(8): 433-442
(  0) 0) |
| [10] |
魏小强, 雷秀丽, 马庆珍. 基于多道奇异谱分析的三维地震数据规则化方法[J]. 石油地球物理勘探, 2014, 49(5): 846-851 (Wei Xiaoqiang, Lei Xiuli, Ma Qingzhen, et al. 3D Seismic Data Regularization Based on Multi-Channel Singular Spectrum Analysis[J]. Oil Geophysical Prospecting, 2014, 49(5): 846-851)
(  0) 0) |
| [11] |
叶沛, 许可, 徐曦煜. 基于奇异谱分析的DGPS浮标海面高程测量误差研究[J]. 遥感技术与应用, 2015, 30(4): 661-666 (Ye Pei, Xu Ke, Xu Xiyu. Study on Denoising the Instrumental Errors of the Sea Surface Height Series Derived from Buoys[J]. Remote Sensing Technology and Application, 2015, 30(4): 661-666)
(  0) 0) |
| [12] |
曹奇, 岳东杰, 王海, 等. 基于奇异谱分析的大桥索塔变形信号提取与分析[J]. 大地测量学与地球动力学, 2014, 34(5): 144-150 (Cao Qi, Yue Dongjie, Wang Hai, et al. Extraction and Analysis of Deformation Signals of Bridge Pylons Based on Singular Spectrum Analysis[J]. Jouranl of Geodesy and Geodynamics, 2014, 34(5): 144-150)
(  0) 0) |
| [13] |
Gruszczynska M, Klos A, Rosat S, et al. Deriving Common Seasonal Signals in GPS Position Time Series by Using Multichannel Singular Spectrum Analysis[J]. Acta Geodynamica et Geomaterialia, 2017, 14(3): 273-281
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

