2. 北京卫星导航中心,北京市,100094
伪距差分、基线解算、网络RTK等差分技术可将用户定位精度提升到cm到mm量级,但需要地面参考站支持,造价高、操作复杂,且服务范围有限,因此一般导航用户更倾向于实时高精度的单点定位。1997年,Zumberge等[1]实现了载波高精度定位,但由于轨道、钟差的精度限制,定位精度并不高。由于码相观测量偏差、硬件延迟等因素,造成载波相位模糊度丧失原本的整数特性,使得精密单点定位解一直处于浮点解状态。近年来,旨在实现单个用户模糊度固定解的PPP-AR模式成为发展热点,小数偏差法(FCBs)、整数相位钟法(IRCs)和去耦钟差法(DC)等理论逐步成熟,并陆续有相应的产品问世[2-5]。但目前仍未有北斗相关参数发播,北斗固定解精密单点定位仍难以实现产业化。
与上述模式需要通过网络接收精密产品及相关模糊度产品不同,广域差分增强系统基于大范围地面监测网络实现差分信息生成并通过GEO卫星进行信息播发,在解算实时性、作用范围方面具有独特的优势,是提升用户定位精度和可靠性的重要途径。基于对地面监测站数据的处理,北斗系统构建了集电离层格网、等效钟差、轨道改正数和分区综合改正数于一体的四重差分改正模型[6-11]。其中,分区综合改正数通过对用户站相位观测量的修正,可实现用户定位过程中模糊度的快速收敛,真正实现免费、实时、快速的高精度导航定位。
本文在北京地区布设测试点进行实地测试,利用实测结果和观测数据后处理结果,对分区综合改正数的效果及不同分区改正数对定位精度的影响进行分析。
1 北斗导航与广域差分模型 1.1 模型介绍北斗广域差分服务提供2.5°×5°(纬度×经度)电离层格网参考值,为用户提供高精度的电离层先验信息。此项改正信息与其他3项改正之间不存在耦合性,可单独使用。
等效钟差和轨道改正数的作用在于削弱基于广播星历计算出的轨道和钟差中存在的误差。其中,等效钟差主要针对卫星钟差和轨道误差的径向分量进行修正,轨道改正数的修正主体为经过等效钟差改正后残余的径向轨道误差以及切向、法向轨道误差。
将中国大陆地区按地域分为若干个分区,每个分区包括多个监测站,以分区为单位生成并播发相位改正数,称为分区综合改正数。用户进行等效钟差和轨道改正后,再利用分区综合改正数进行相位观测量修正,经过一定的收敛过程可实现高精度的单点定位。
1.2 参数使用方法假设用户端消电离层组合伪距和相位观测量分别为(省略硬件延迟项、潮汐误差等):
| $ \begin{array}{*{20}{c}} {P = \rho + c\left( {{\rm{d}}{t_{\rm{r}}} - {\rm{d}}{t^{\rm{s}}}} \right) + T + {\varepsilon _P}}\\ {\mathit{\Phi } = \rho + c\left( {{\rm{d}}{t_{\rm{r}}} - {\rm{d}}{t^{\rm{s}}}} \right) + T + \lambda N + W + {\varepsilon _\mathit{\Phi }}} \end{array} $ | (1) |
式中,ρ为用广播轨道和测站位置计算的站星距离,ρ=‖coorsat-coorrec‖;dtr、dts为测站钟差和广播钟差,T、W为对流层延迟误差和相位缠绕误差;λ、N为消电离层组合波长和模糊度;εP、εΦ为消电离层组合的伪距和相位噪声。
用户收到的改正数包括等效钟差esc、轨道改正数dorb、分区改正数dzone。分区改正数可表述为:
| $ d_{\mathrm{zone}}=\mathrm{d} \rho_{\mathrm{r}}+c \delta t_{\mathrm{r}}-c \delta t^{\mathrm{s}}+\mathrm{d} T+\lambda_{\mathrm{IF}} \mathrm{d} N+\varepsilon_{L_{\mathrm{IF}}} $ | (2) |
式中,δtr、δts为分区主参考站处的站钟残余误差和经过等效钟差改正后的卫星残余钟差,dT、dN为分区主参考站处的对流层未模型化误差和计算分区改正数时的模糊度初值与模糊度真实值之间的偏差。
经过差分参数改正后的观测模型为:
| $ \begin{aligned} P=& \rho^{\prime}+c\left(\mathrm{d} t_{\mathrm{r}}-\mathrm{d} t^{\mathrm{s}}-\mathrm{esc}\right)+T+\varepsilon_{P} \\ \mathit{\Phi }=& \rho^{\prime}+c\left(\mathrm{d} t_{\mathrm{r}}-\mathrm{d} t^{\mathrm{s}}-\mathrm{esc}\right)+\\ & T+\lambda N+d_{\mathrm{zome}}+W+\varepsilon_{\mathit{\Phi }} \end{aligned} $ | (3) |
式中,ρ′=‖coorsat+dorb-coorrec‖,为经轨道改正数修正后的站星距离。
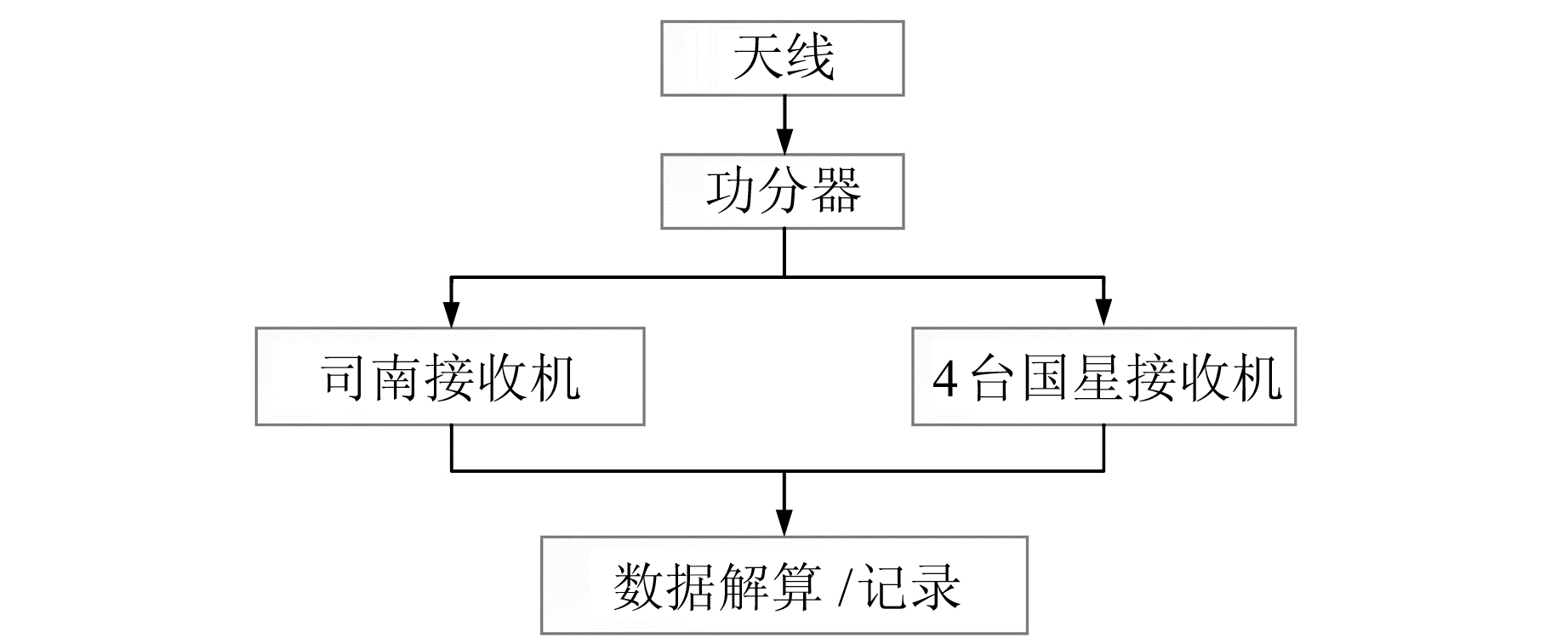
2 实验验证为验证分区综合改正数的稳定性及增强效果,在北京卫星导航中心楼顶布设测试点,采用多接收机共用天线的形式进行实验。测试过程中进行实时定位测试,并采集原始观测数据进行后处理。测试点位基准坐标采用GPS事后静态PPP结果。设备连接情况见图 1,参数设置见表 1。
|
图 1 设备安装示意图 Fig. 1 Detail of equipment connection |
|
|
表 1 实时数据解算参数设置 Tab. 1 Parameters settings of real-time position resolution |
国星1号接收机不进行分区定位,采用B3频点伪距定位;其余国星接收机固定选择一个分区进行解算,其中No.1分区距测试点3 km,No.2分区距测试点约1 050 km,No.4分区距测试点约600 km;司南接收机采用自主选择分区模式。数据采集细节见表 2。
|
|
表 2 观测数据采集详情 Tab. 2 Details of observation data |
在2017-07-27~08-02(doy 208~214)采用5台接收机进行实时位置解算,接收机工作模式按表 1设置。
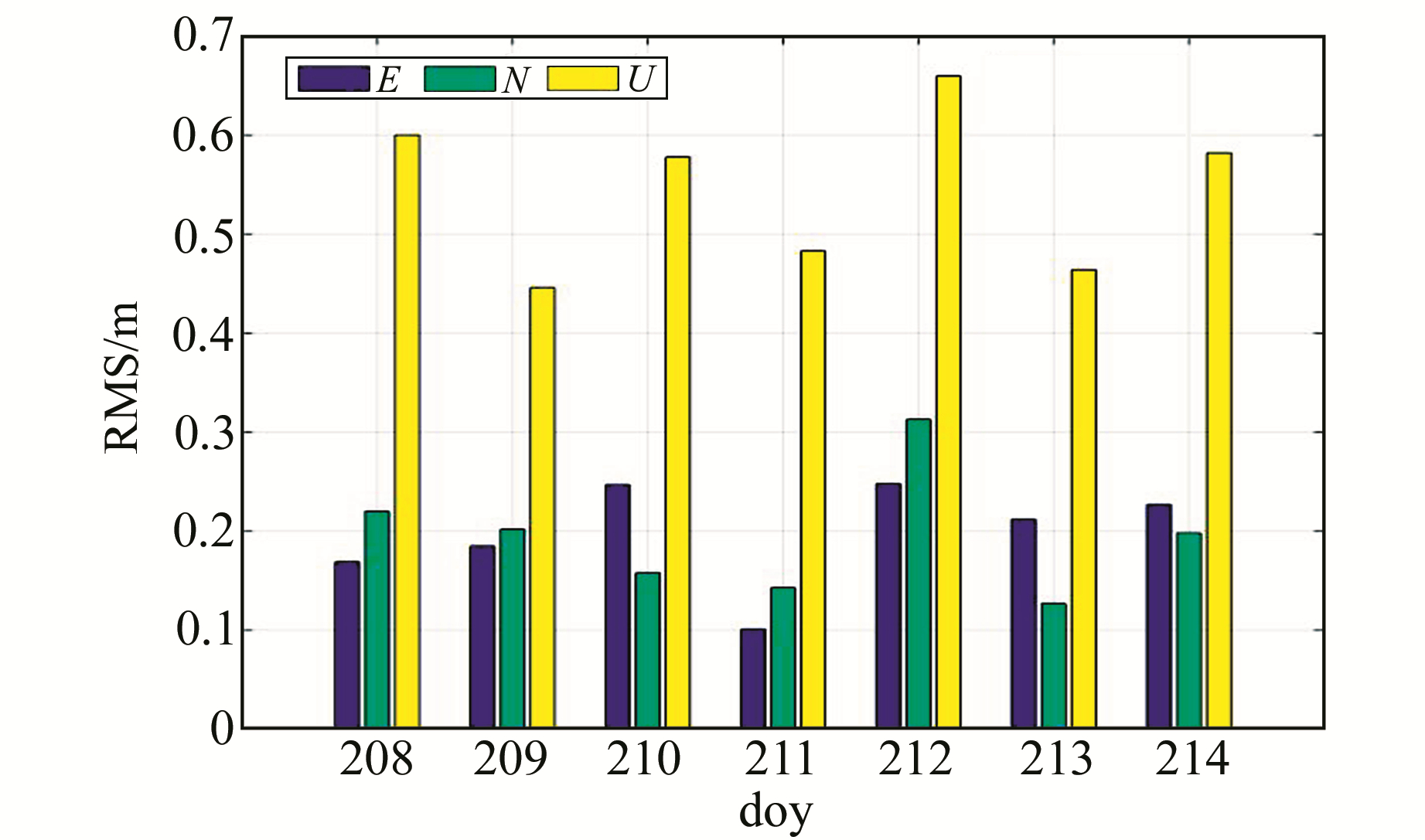
司南M300接收机实时定位结果RMS见图 2。司南B1B2实时分区定位结果除doy212较差外,其余几天都较平稳。其原因是,doy212实测过程中多次出现数据中断,发生重收敛现象,造成定位结果的RMS偏大。
|
图 2 司南接收机实测定位结果统计 Fig. 2 Real-time positioning result of ComNav receiver |
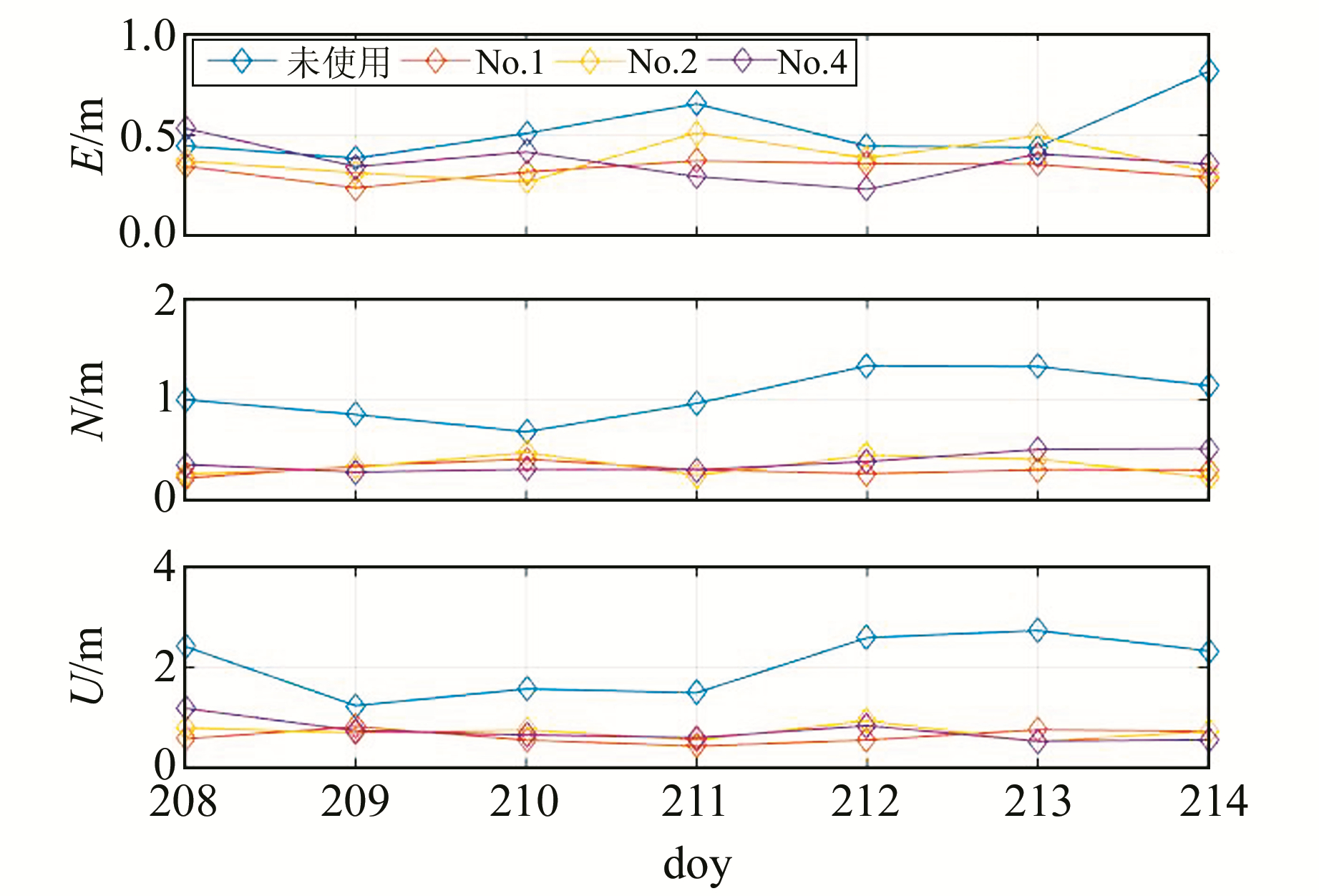
国星4台用户机定位结果见图 3。
|
图 3 国星用户机实测定位结果统计(RMS) Fig. 3 Real-time positioning results of Guoxing receivers (RMS) |
综合测试期间7 d的定位结果,实时位置解算结果的RMS见表 3。由结果可知,B1B2双频消电离层分区定位的精度可达到N、E方向0.20 m(水平方向0.3 m)、高程方向0.55 m以内。国星用户机采用B3单频进行定位解算,未升级的用户机定位过程中无法使用分区改正数,且定位过程中未采用半和模型,定位结果可代表现有单频导航接收机定位水平,其精度可实现水平方向2 m、高程方向3 m以内。
|
|
表 3 接收机实时定位结果RMS Tab. 3 RMS of real-time positioning results |
由图 3可知,分区改正数的加入可使定位精度获得明显提高,且实际测试过程中用到的3个不同分区的定位精度并未出现明显差异。N、E方向定位精度均可实现0.40 m以内(水平方向定位精度0.55 m),高程方向定位精度0.80 m以内。
分区改正数为相位改正数,为了达到较高的定位精度,需要进行收敛。收敛过程中,定位精度稍差;收敛结束后,定位结果趋于稳定。在表 3定位结果统计中包含了收敛弧段,若仅统计收敛后的定位结果,统计精度有望进一步提高。
2.2 后处理分区定位结果为规避实时解算涉及到的通信延迟、数据缺失等,探究不同分区对差分定位的影响,利用采集的原始观测数据,并收集对应时间段的差分改正信息,采用离线定位程序进行分区定位解算。解算参数设置见表 4。鉴于分区改正信息中包含参考站处的残余对流层误差,在用户端定位时不估计对流层残余误差。
|
|
表 4 后处理数据解算参数设置 Tab. 4 Details of post processing |
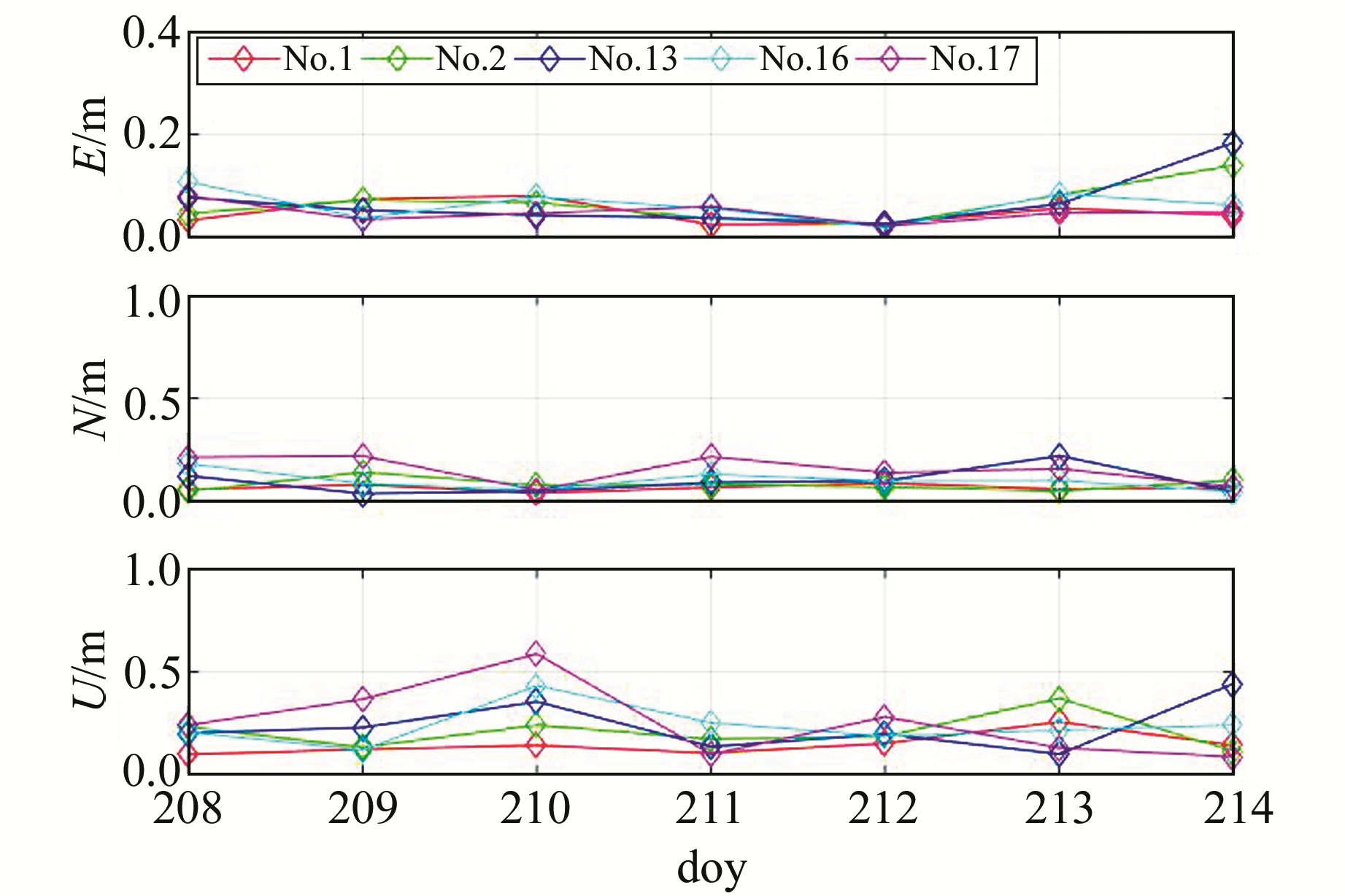
采用不同分区的分区综合改正数进行静态模式后处理的RMS见图 4。
|
图 4 后处理静态解算定位结果(RMS) Fig. 4 Results of post processed static positioning(RMS) |
以doy211为例,分析不同分区定位结果之间的差异(图 5)。可见,采用不同的分区,在分区改正数稳定、连续的情况下,均可实现定位结果的收敛。但选用不同分区改正信息,收敛速度不同。以doy211静态定位结果的收敛阶段为例(doy211 00:00~01:00),将图 5进行局部放大,见图 6。
|
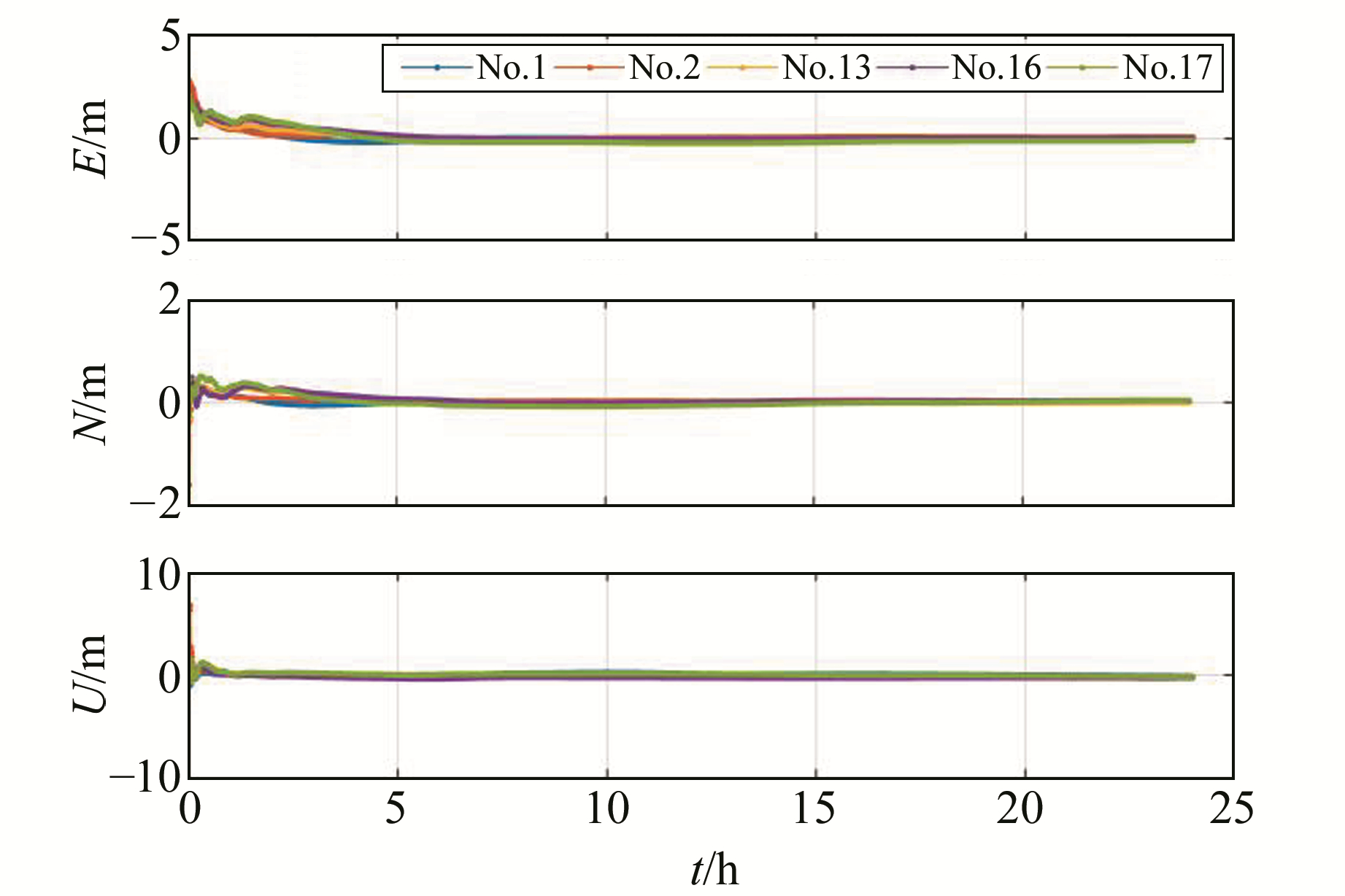
图 5 后处理静态解算结果(doy211) Fig. 5 Results of post processed static positioning(doy211) |

|
图 6 Doy211不同分区改正数定位收敛阶段示意图 Fig. 6 Convergence period of differential positioning using different zone corrections |
采用距离最近的No.1分区的改正信息时(蓝色),N方向及U方向收敛速度明显快于其他分区;No.17分区(棕色)距离测试点位最远,收敛速度最慢,且收敛过程存在波动的情况。
采用动态模式进行数据解算,结果见图 7。

|
图 7 后处理动态解算定位结果(RMS) Fig. 7 Results of post processed kinematic positioning (RMS) |
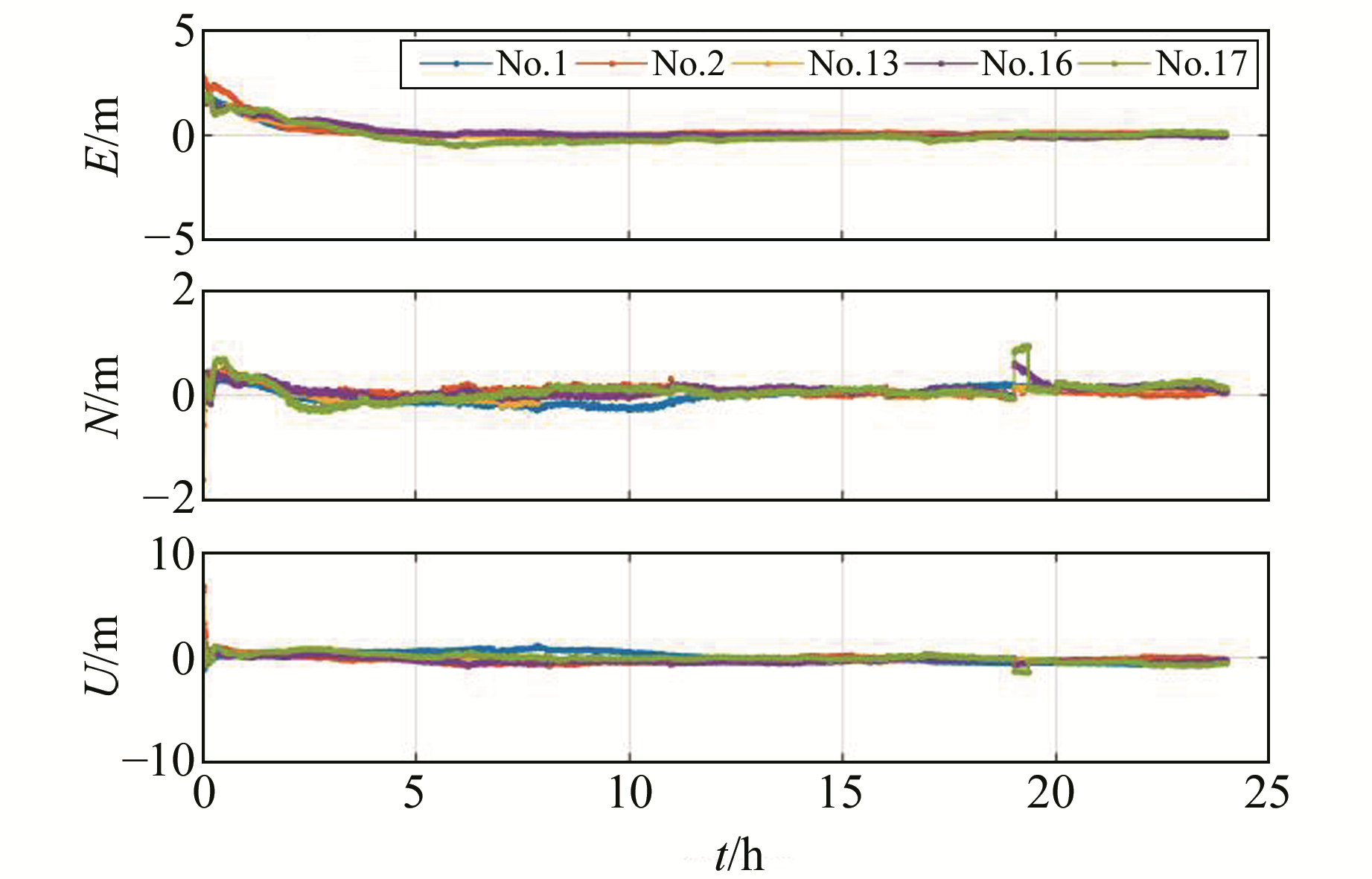
在doy211的19:00,No.16和No.17分区解算分区综合改正数时,主参考站发生切换,导致分区改正数在19:00发生轻微跳变(图 8),引起模糊度跳变,出现重收敛现象。其余时间段分区改正信息连续、稳定,收敛效果良好。
|
图 8 后处理动态解算结果(doy211) Fig. 8 Results of post processed kinematic positioning (doy 211) |
将事后处理结果进行综合统计,见表 5。
|
|
表 5 不同分区改正数后处理定位结果RMS Tab. 5 Post processing results of positioning using different zone corrections(RMS) |
同样采用动态模式解算,表 5和表 3所示定位结果存在一定差异,原因包括以下2个方面:
1) 实时解算可能存在由于通信问题产生的差分数据中断情况,差分数据尤其是分区改正信息若长时间中断,会造成模糊度跳变,影响数据收敛状态的维持。
2) 北斗广域差分信息中不同参数之间的更新频率不同,在使用过程中需严格进行参数时间的对齐。改正参数错位会造成差分信息与广播星历及钟差之间的不匹配,影响差分效果。
由表 6可知,采用不同分区的分区改正数进行静态解算,单天解并未呈现明显差异,即分区综合改正数的作用范围并不局限于1 000 km以内。除No.1分区外,其他分区改正数的静态解算单天解结果在N方向定位精度十分接近,E方向除No.17分区外均可达到10 cm以内。No.17位于新疆地区,属于北斗系统服务区西侧,而C04星位于最东端,No.17分区中无C04星的改正值,造成定位过程中东西方向定位结果发生倾斜。
|
|
表 6 不同分区静态解算收敛结果 Tab. 6 Final position of post processed static positioning using different zone corrections in static mode |
分区综合改正数针对经等效钟差和轨道改正数修正后的剩余轨道残余误差和卫星钟差误差进行修正,在修正的同时引入了一部分对流层延迟误差、参考站站钟误差和模糊度偏差,站钟误差在用户端计算时可以被吸收到测站钟差中,模糊度偏差项也可以被吸收到测站浮点解模糊度项中,在分区改正数稳定情况下不会影响用户定位的稳定性。
No.17分区平均海拔1 300 m,No.1分区平均海拔约40 m,No.2分区平均海拔约180 m,No.16分区平均海拔约800 m,No.13分区平均海拔2 800 m,分区参考站之间存在较大的海拔差异,对流层参数的模型误差引入到分区改正数中造成不同分区高程定位结果之间存在差异,解算结果增加了不确定性。
3 结语1) 经实测验证,单频伪距用户利用北斗广域差分服务中的等效钟差进行伪距差分定位,定位精度可达到水平方向2 m、高程方向3 m。加入轨道改正数和分区综合改正数后,B3单频定位精度可达到水平方向0.55 m、高程方向0.80 m。
2) 加入分区改正信息后,B1B2双频定位精度可达到水平方向0.30 m、高程方向0.55 m,优于导航型接收机B3单频定位精度。
3) 在差分信息连续、稳定的情况下,分区定位精度动态可达到水平方向0.35 m、高程方向0.50 m,静态可达水平方向0.12 m、高程方向0.22 m。
4) 分区定位选择不同分区对动态定位结果无明显影响。采用不同分区的改正信息,定位结果的RMS基本一致。但由于不同分区改正数中对流层延迟的差异造成采用不同分区改正数用于静态解算时,其收敛结果略有差异。所以,在选择分区改正数时,应尽可能选择距离近的分区。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B3): 5005-5017 DOI:10.1029/96JB03860
(  0) 0) |
| [2] |
Laurichesse D. The CNES Real-time PPP with Undifferenced Integer Ambiguity Resolution Demonstrator[C]. International Technical Meeting of the Satellite Division of the Institute of Navigation, 2011
(  0) 0) |
| [3] |
Ge M, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399 DOI:10.1007/s00190-007-0187-4
(  0) 0) |
| [4] |
Geng J, Meng X, Dodson A H, et al. Rapid Re-Convergences to Ambiguity-fixed Solutions in Precise Point Positioning[J]. Journal of Geodesy, 2010, 84(12): 705-714 DOI:10.1007/s00190-010-0404-4
(  0) 0) |
| [5] |
Kazmierski K, Sošnica K, Hadas T. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-time Precise Point Positioning[J]. GPS Solutions, 2018, 22(1): 11 DOI:10.1007/s10291-017-0678-6
(  0) 0) |
| [6] |
曹月玲. Beidou区域导航系统广域差分及完好性监测研究[D].北京: 中国科学院大学, 2014 (Cao Yueling. Studies on the Wide-Area Differential Correction and Integrity Monitoring for the Regional Satellite Navigation System of Beidou[D]. Beijing: University of Chinese Academy of Sciences, 2014) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2614649
(  0) 0) |
| [7] |
杨赛男.北斗分米级星基增强系统关键技术研究及精度评估[D].北京: 中国科学院大学, 2017 (Yang Sainan. Research on BDS Decimeter Level SBAS and Its Performance Assessment[D]. Beijing: University of Chinese Academy of Sciences, 2017)
(  0) 0) |
| [8] |
张益泽.北斗实时高精度定位服务系统研究[D].上海: 同济大学, 2017 (Zhang Yize. Research on Real-Time High Precision Beidou Positioning Service System[D]. Shanghai: Tongji University, 2017) http://d.old.wanfangdata.com.cn/Periodical/chxb201809018
(  0) 0) |
| [9] |
陈俊平, 胡一帆, 张益泽, 等. 北斗星基增强系统性能提升初步评估[J]. 同济大学学报:自然科学版, 2017, 45(7): 1075-1082 (Chen Junping, Hu Yifan, Zhang Yize, et al. Preliminary Evaluation of Performance of Beidou Satellite-Based Augmentation System[J]. Journal of Tongji University:Natural Science, 2017, 45(7): 1075-1082)
(  0) 0) |
| [10] |
Chen J P, Zhang Y Z, Yang S N, et al. A New Approach for Satellite Based GNSS Augmentation System: from Sub-meter to Better than 0.2 Meter Era[C].Pacific Pnt, Honolulu, 2015
(  0) 0) |
| [11] |
陈俊平, 杨赛男, 周建华, 等. 综合伪距相位观测的北斗导航系统广域差分模型[J]. 测绘学报, 2017, 46(5): 537-546 (Chen Junping, Yang Sainan, Zhou Jianhua, et al. A Pseudo-range and Phase Combined SBAS Differential Correction Model[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 537-546)
(  0) 0) |
| [12] |
Gao Y, Shen X B. A New Method for Carrier-Phase-Based Precise Point Positioning[J]. Navigation, 2002, 49(2): 109-116 DOI:10.1002/navi.2002.49.issue-2
(  0) 0) |
2. Beijing Satellite Navigation Center, Beijing 100094, China
 2019, Vol. 39
2019, Vol. 39

