电离层延迟是全球导航卫星系统(global navigation satellite system,GNSS)定位的主要误差源之一,从天顶到地平方向,电离层延迟引起的测距误差可达5~150 m[1-2]。双差定位技术是当前高精度GNSS用户常采用的数据处理技术。该技术一般用双频消电离层组合观测值来消除一阶电离层延迟的影响,但残余的高阶电离层延迟对定位精度的影响仍可达数mm[3],这对于地壳形变监测、地震灾害预报、亚mm级全球坐标框架建立与维护、板块运动监测等高精度大地测量应用和研究是不容忽略的。正因如此,高阶电离层延迟误差改正近年来逐渐引起国内外学者的重视[4-8]。
目前,已有学者基于IGS全球网数据分析研究了高阶电离层延迟对高精度定位、卫星轨道钟差、速度场及参考框架建立等的影响[9-15],但上述研究主要是针对GNSS全球网数据,所用站点的空间跨度过大,研究不够精细[16-17],不能反映高阶电离层延迟对中国区域GNSS影响的时空分布规律。本文利用中国大陆构造环境监测网络(crustal movement observation network of China,CMONOC,以下简称“陆态网”)2015年的GNSS数据,系统研究高阶电离层延迟对中国区域双差定位的影响及其时空分布规律。
1 顾及高阶电离层延迟改正的双差定位模型顾及高阶电离层延迟改正的载波相位和伪距观测方程见文献[18-20]。
在利用双频消电离层组合消除电离层延迟一阶项的影响后,基于L3(双频消电离层组合相位观测值)[18-20],先站间求差,再星间求差,构建双差定位模型:
| $ L_{3\kappa \vartheta }^{ij} = \rho _{\kappa \vartheta }^{ij} + \Delta I_{2\kappa \vartheta }^{ij} + \Delta I_{3\kappa \vartheta }^{ij} + B_{3\kappa \vartheta }^{ij} - {\varepsilon _{L_{_{3\kappa\vartheta }}^{ij}}} $ | (1) |
其中,
| $ \begin{aligned} \Delta I_{2 \kappa \vartheta}^{i j} &=\frac{q_{\kappa}^{i}-q_{\vartheta}^{i}-q_{\kappa}^{j}+q_{\vartheta}^{j}}{2 f_{1} f_{2}\left(f_{1}+f_{2}\right)} \\ \Delta I_{3 \kappa\vartheta}^{i j} &=\frac{t_{\kappa}^{i}-t_{\vartheta}^{i}-t_{\kappa}^{j}+t_{\vartheta}^{j}}{3 f_{1}^{2} f_{2}^{2}} \end{aligned} $ |
式中,κ、ϑ为测站编号,i、j为卫星编号。
计算高阶电离层延迟时需已知总电子含量TEC(total electronic content)、地磁场矢量
| $ F(z)=\frac{\operatorname{STEC}}{\mathrm{VTEC}} $ | (2) |
其中,
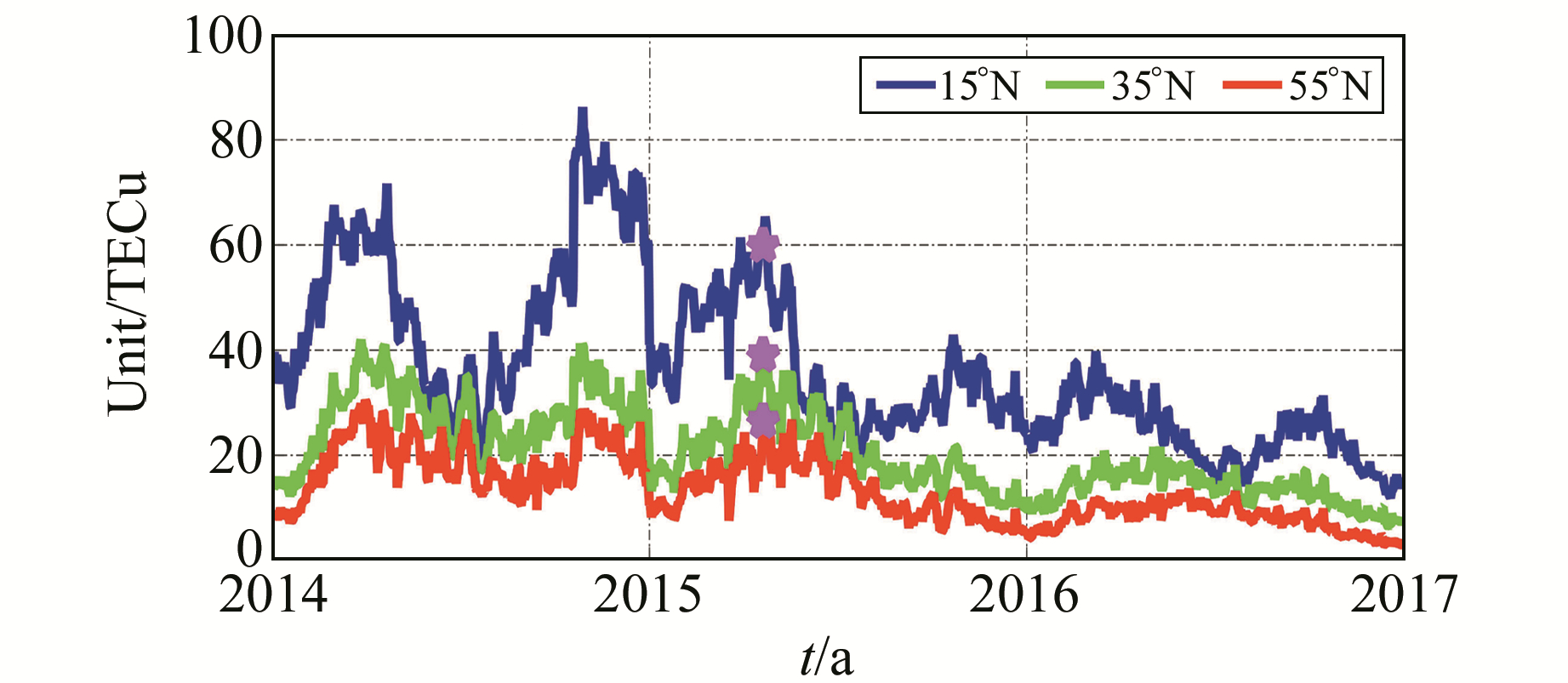
高阶电离层延迟对L3的影响与电离层活动强度相关,VTEC能较准确地衡量电离层活动强度。本文在分析高阶电离层延迟对L3影响之前,先分析VTEC时空分布。从欧洲定轨中心(CODE)下载2014~2016年GIM数据产品,抽取中国区域中心经纬度(105°E,15°N)、(105°E,35°N)和(105°E,55°N)2014~2016年VTEC的单天均值,结果见图 1。由图 1可知,中国区域VTEC有1 a和0.5 a规律变化,2014年和2015年变化幅度明显大于2016年,约为10~80 TECu。2014年及2015年中国区域VTEC均有双峰值,2015年较大峰值的年积日为110(图 1星号所示)。
|
图 1 中国区域VTEC时间序列 Fig. 1 Time series of VTEC in China region |
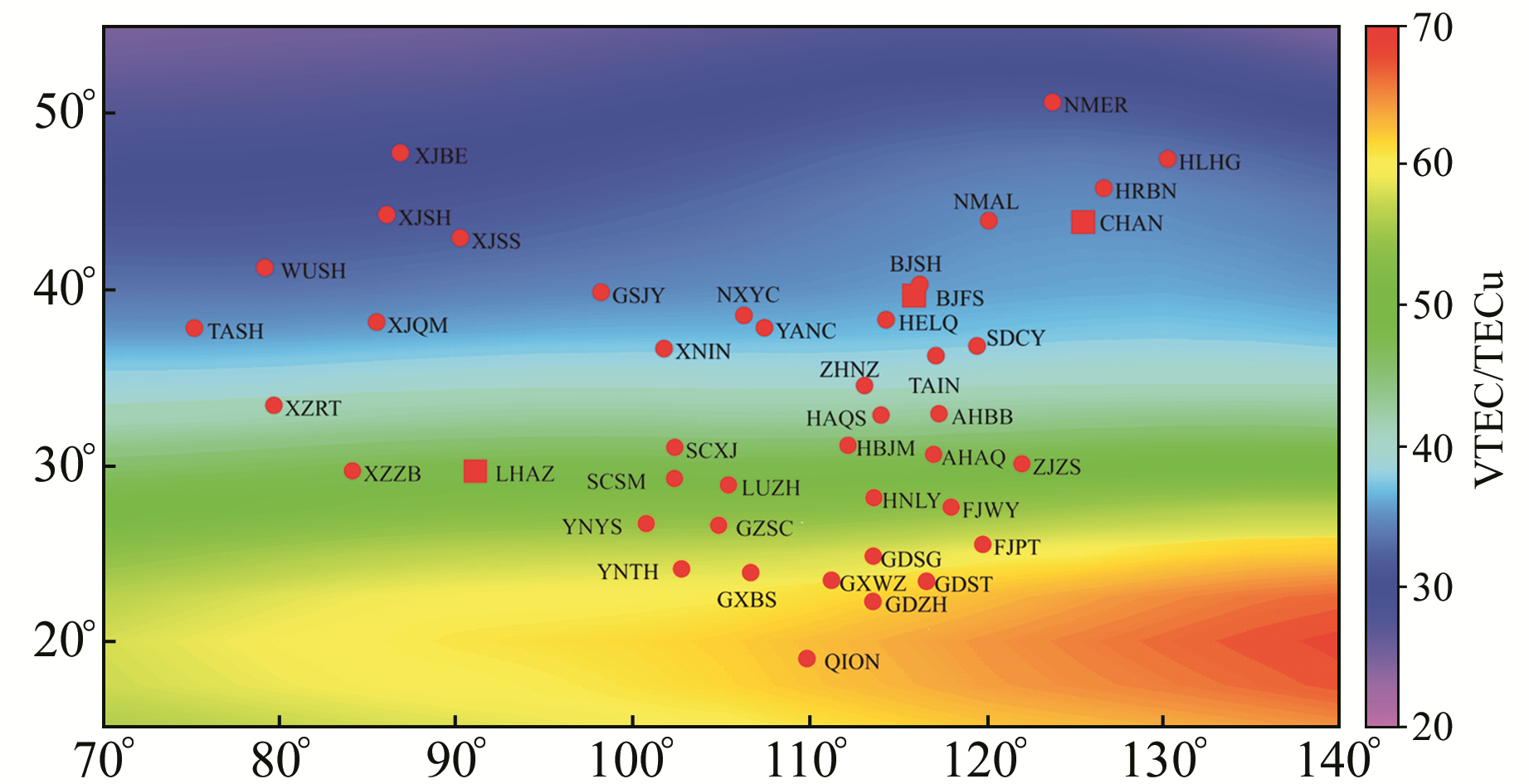
取2015年第110 d的GIM数据,提取中国区域(70°~140°E,15°~55°N)VTEC的单天均值,结果见图 2。结果表明,随着地理纬度的减小,中国区域VTEC明显有增大趋势,从55°N到15°N,VTEC从约20 TECu增大到70 TECu。
|
图 2 实验数据分布 Fig. 2 Distribution map of experimental data |
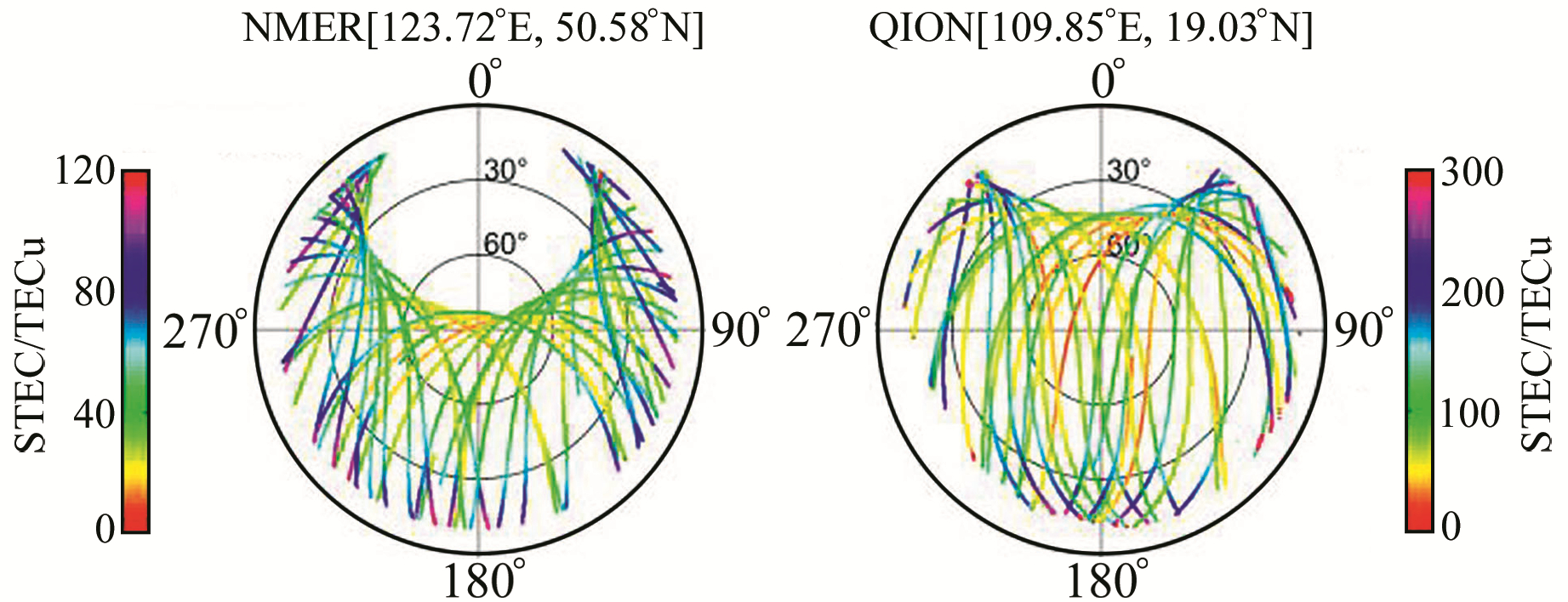
以2015年第110 d陆态网高纬度测站NMER和低纬度测站QION的GNSS观测数据为例,先分析陆态网站点STEC的时空变化,再分析高阶电离层延迟对陆态网站点L3的影响,分析软件为RINEX_HO软件[21]。分析结果见图 3~5,底图都为卫星天空图(截止高度角为10°),卫星轨迹点填充颜色分别代表STEC值、二阶电离层延迟影响值和三阶电离层延迟影响值。
|
图 3 NMER站和QION站STEC Fig. 3 STEC of stations NMER and QION |

|
图 4 二阶电离层延迟对L3的影响(ΔI2) Fig. 4 Second-order ionospheric effect on L3(ΔI2) |
|
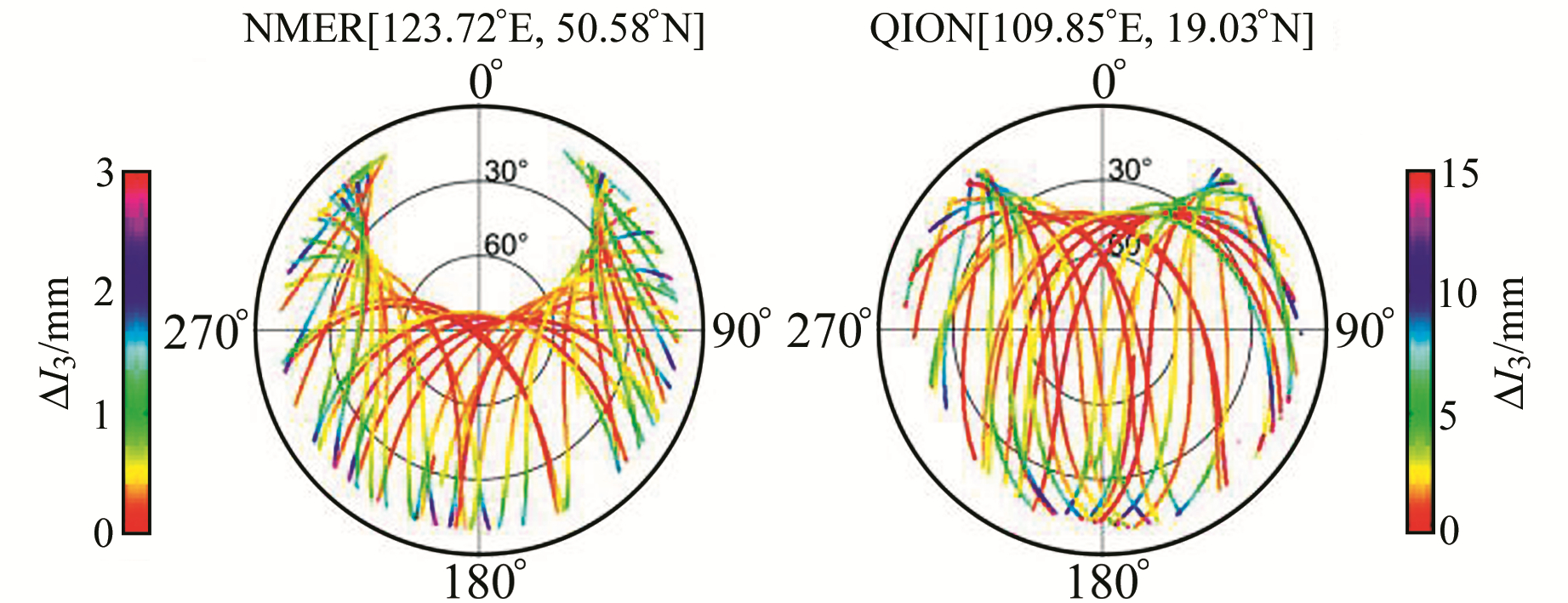
图 5 三阶电离层延迟对L3的影响(ΔI3) Fig. 5 Third-order ionospheric effect on L3(ΔI3) |
由图 3可知,NMER站和QION站的STEC与测站地理纬度和卫星高度角相关,测站地理纬度越小,卫星高度角越小,STEC就越大;NMER站的STEC约为10~120 TECu,QION站的STEC最大可达280 TECu。
由图 4和图 5可知,高阶电离层延迟对L3的影响同样与测站地理纬度和卫星高度角相关,测站地理纬度越小,卫星高度角越小,影响量值就越大。高阶电离层延迟对NMER站和QION站L3均影响明显,二阶电离层延迟对NMER站影响约为0~1.5 cm,对QION站影响较NMER站大,可达3.5 cm;三阶电离层延迟对NMER站影响约为0~3 mm,对QION站影响可达1.5 cm。对比图 4和图 5不难发现,二阶和三阶电离层延迟对L3的影响有符号性差异,三阶电离层延迟对L3的影响都为正值,二阶电离层延迟对L3的影响既有正值也有负值,正负号与卫星方位角有关。
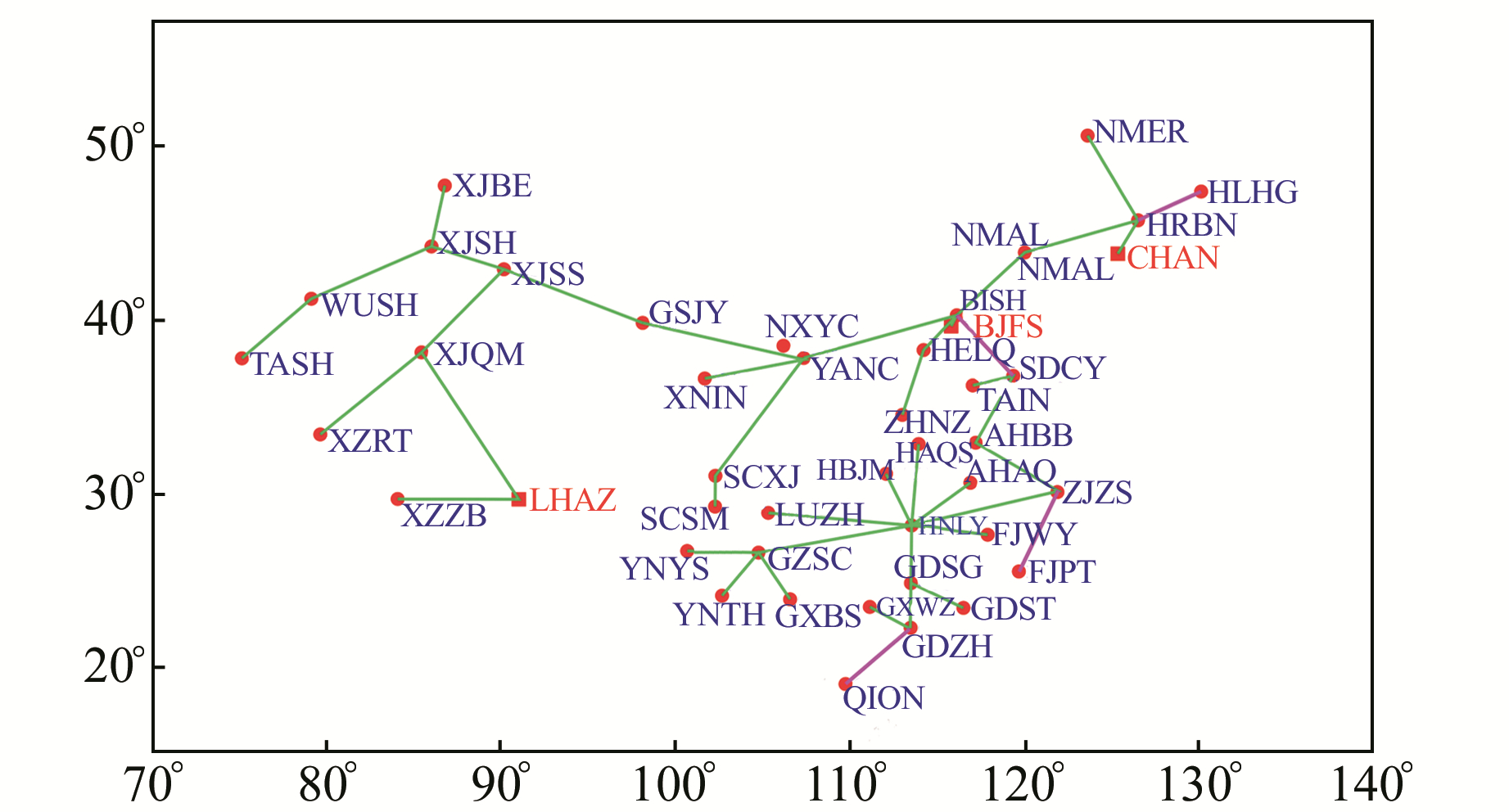
2.3 高阶电离层延迟对中国区域双差定位的影响 2.3.1 实验数据及数据处理策略实验选取41个陆态网测站和3个境内IGS站(约束参考框架到IGB08)2015年GNSS观测数据,具体站点分布见图 2(圆点为陆态网站点,方点为IGS站点,底图为中国区域VTEC空间分布)。解算过程中所需的全球电离层格网模型文件和码偏差文件由欧洲定轨中心(CODE)提供,精密星历、精密钟差和地球自转参数文件从IGS获得;采用VMF产品对对流层延迟进行改正;大气潮和海潮文件通过提交测站近似坐标至相应网站自动生成。
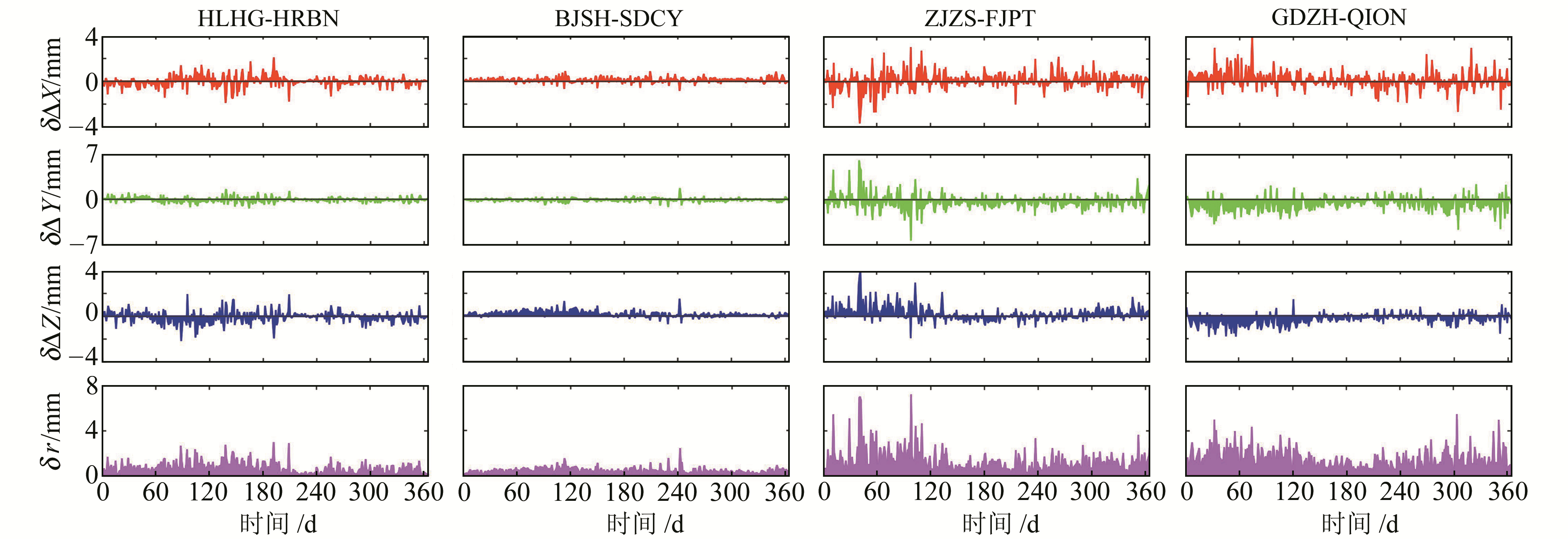
2.3.2 高阶电离层延迟对基线向量的影响在分析高阶电离层延迟对中国区域双差定位单天解的影响之前,先分析高阶电离层延迟对基线向量的影响。用Bernese 5.2[22]软件对所选测站进行考虑、不考虑高阶电离层延迟的对比处理,数据处理过程中所构建的独立基线见图 6,从中选取4条独立基线进行对比分析(基线解算时段长度为24 h),结果见图 7和表 1。图 7给出了2015年4条独立基线顾及和未顾及高阶电离层延迟改正的较差,表 1给出了4条基线的概况和影响较差年均值。图 7中的δr=
|
图 6 数据处理过程中构建的独立基线 Fig. 6 Independent baselines during data processing |
|
图 7 高阶电离层延迟对基线的影响 Fig. 7 Higher-order ionospheric effect on baselines |
|
|
表 1 高阶电离层延迟对基线向量影响的统计 Tab. 1 Annual mean values of higher-order ionospheric effect on baseline vectors |
图 7和表 1表明,高阶电离层延迟对基线向量的影响与基线所处纬度相关,对中高纬度基线影响较小,δr年均值在0.5 mm左右;对低纬度基线影响较大,δr超过1 mm。此外,低纬度基线ZJZS-FJPT和GDZH-QION的δr时间序列有0.5 a周期变化趋势。
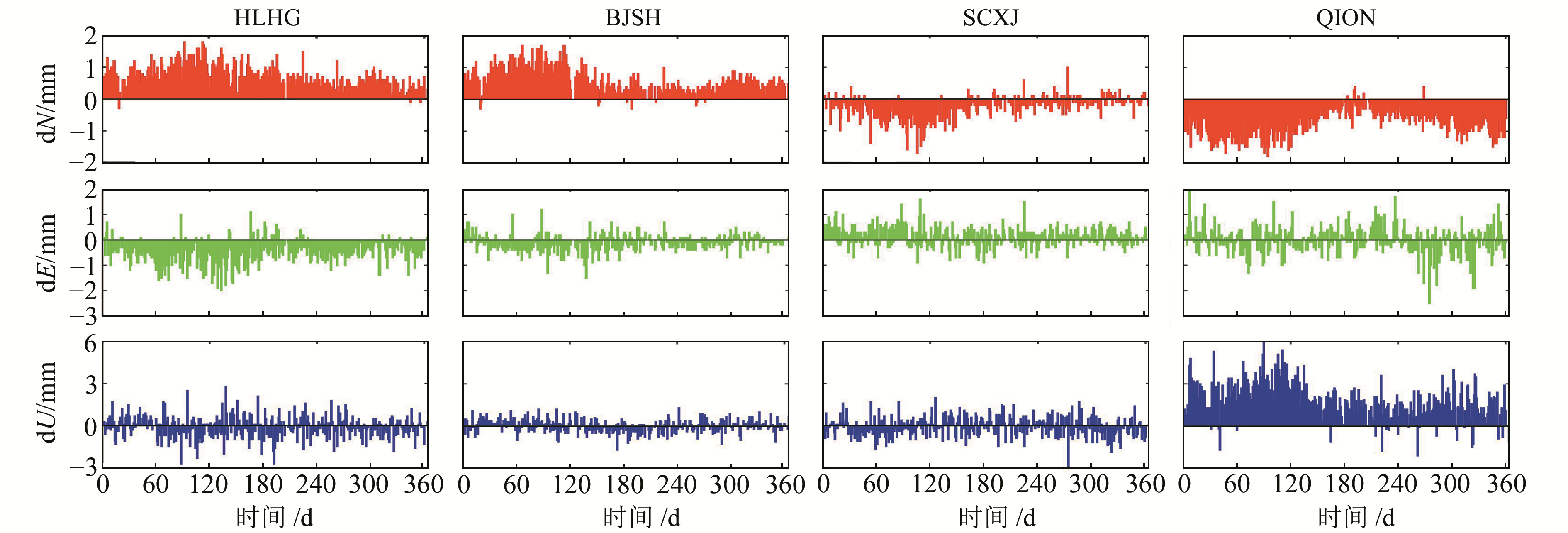
2.3.3 高阶电离层延迟对双差定位影响的时空分布规律为分析高阶电离层延迟对中国区域双差定位单天解的影响,用Bernese 5.2软件对所选测站GNSS数据进行加、不加高阶电离层延迟改正的对比处理,得到各站双差定位结果在N、E、U方向上的互差。高(HLHG、BJSH)、中(SCXJ)、低(QION)纬度测站的互差时间序列见图 8,横轴表示年积日,纵轴表示顾及高阶电离层延迟改正和未顾及高阶电离层延迟改正的双差定位结果在N、E、U方向上的互差。
|
图 8 高阶电离层延迟定位误差时间序列 Fig. 8 Time series of higher-order ionospheric positioning errors |
由图 8可知,高阶电离层延迟对中国区域双差定位的影响(考虑与不考虑高阶电离层影响时定位结果的差异)有0.5 a的周期变化和方向性差异,不再具有随测站纬度减小而增大的规律。高阶电离层延迟对高纬度测站HLHG和低纬度测站QION双差定位的影响都较大,不同的是高阶电离层延迟对HLHG站N方向影响为正值,对QION站N方向影响为负值。就低纬度测站QION而言,N方向和U方向均有明显的0.5 a周期变化,且具有系统性,U方向影响最大,可达6 mm,N方向影响次之,约为0~2 mm,E方向影响最小,只有1 mm左右。
对2015年各测站N、E、U方向互差时间序列取均值,得到高阶电离层延迟对各测站双差定位的全年影响值,结果见图 9,其中箭头代表高阶电离层延迟对各测站双差定位N方向和E方向影响的年均值,测站点填充浓度代表高阶电离层延迟对各测站双差定位U方向影响的年均值。

|
图 9 高阶电离层延迟定位误差空间分布 Fig. 9 Spatial distribution of higher-order ionospheric positioning errors |
由图 9可知,高阶电离层延迟对中国地区双差定位的影响与测站位置相关,存在明显的方向性差异:N方向影响年均值普遍较大,约0~1 mm,高纬度测站(35°~55°N)呈向北偏移趋势,低纬度测站(15°~35°N)呈向南偏移趋势;E方向影响年均值最小,约0~0.5 mm,有向西偏移趋势;U方向低纬度测站(15°~25°N)影响年均值最大,约0~2 mm,呈向上偏移趋势,高纬度测站(25°~55°N)小于0.5 mm。
高阶电离层延迟对双差定位的影响与TEC和测站网型结构有关[11]。低纬度测站较高纬度测站有更大的TEC值,故高阶电离层延迟对低纬度测站L3的影响大于高纬度测站;低纬度基线较中高纬度基线有更大的TEC值,故高阶电离层延迟对低纬度基线的影响要大于中高纬度基线。但双差定位网平差算法对高阶电离层延迟误差进行了重新分配,致使高阶电离层延迟对双差定位的影响出现高纬度测站向北偏移、低纬度测站向南偏移这一现象。
3 结语以顾及高阶电离层延迟的双差定位模型为基础,探讨中国区域VTEC的时空变化规律,分析高阶电离层延迟对L3的影响。通过分析我国陆态网的数据,系统研究高阶电离层延迟对中国区域双差定位的影响,得出以下结论:
1) 中国区域VTEC有1 a和0.5 a的周期变化规律,低纬度地区的VTEC明显大于高纬度地区。
2) 高阶电离层延迟对L3的影响可达cm级,与测站地理纬度和卫星高度角相关,测站地理纬度越小,卫星高度角越小,影响量值越大;二阶和三阶电离层延迟对L3的影响有符号性差异,三阶电离层延迟对L3的影响都为正值,二阶电离层延迟对L3的影响既有正值也有负值,正负号与卫星方位角相关。
3) 高阶电离层延迟对基线向量的影响与基线所处纬度相关,对低纬度基线的影响较大,影响年均值超过1 mm;对中高纬度基线的影响较小,影响年均值在0.5 mm左右。高阶电离层对中国区域双差定位的影响与测站网型结构相关,存在0.5 a的周期变化规律,且具有方向性差异,高纬度测站呈向北偏移趋势,低纬度测站呈向南偏移趋势;N方向影响年均值普遍较大,约0~1 mm,E方向影响年均值最小,约0~0.5 mm,U方向低纬度测站影响年均值最大,约0~2 mm。
综合以上结论,在中国区域进行高精度双差定位数据处理时,应考虑高阶电离层延迟对定位的影响,尤其是电离层活跃的低纬度地区。
| [1] |
范胜军.顾及地磁场影响的电离层高阶项改正算法研究[D].武汉: 武汉大学, 2005 (Fan Shengjun. Research on Corrected Higher-Order Ionospheric Delay Error with Geomagnetic Effect[D]. Wuhan: Wuhan University, 2005) http://cdmd.cnki.com.cn/Article/CDMD-10486-2006032462.htm
(  0) 0) |
| [2] |
王虎.GPS精密单点定位中电离层延迟改正模型的研究与分析[D].长沙: 中南大学, 2008 (Wang Hu. Research on the Model of Ionospheric Delay Correction in GPS Precise Point Positioning[D]. Changsha: Central South University, 2008)) http://cdmd.cnki.com.cn/Article/CDMD-10533-2008167703.htm
(  0) 0) |
| [3] |
匡翠林, 金蕾. 精密单点定位的高阶电离层误差改正研究[J]. 武汉大学学报:信息科学版, 2013, 38(8): 888-891 (Kuang Cuilin, Jin Lei. Higher-Order Ionospheric Error Correction for Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 888-891)
(  0) 0) |
| [4] |
张双成, 涂锐, 张勤, 等. 电离层二阶项模型的构建及其变化规律分析研究[J]. 测绘学报, 2011, 40(增1): 105-110 (Zhang Shuangcheng, Tu Rui, Zhang Qin, et al. The Establishment of Ionospheric Second-Order Model and the Analysis of Ionospheric Variation[J]. Acta Geodatica et Cartographica Sinica, 2011, 40(S1): 105-110)
(  0) 0) |
| [5] |
Wang Z M, Wu Y, Zhang K F, et al. Triple-Frequency Method for High-Order Ionospheric Refractive Error Modelling in GPS Modernization[J]. Journal of Global Positioning Systems, 2005, 4(1-2): 291-295
(  0) 0) |
| [6] |
Hoque M M, Jakowski N. Higher Order Ionospheric Effects in Precise GNSS Positioning[J]. Journal of Geodesy, 2007, 81(4): 259-268 DOI:10.1007/s00190-006-0106-0
(  0) 0) |
| [7] |
Pireaux S, Defraigne P, Wauters L, et al. Higher-Order Ionospheric Effects in GPS Time and Frequency Transfer[J]. GPS Solutions, 2010, 14(3): 267-277 DOI:10.1007/s10291-009-0152-1
(  0) 0) |
| [8] |
邓连生, 姜卫平, 李昭, 等. 电离层高阶项改正对参考框架实现及测站坐标的影响分析[J]. 武汉大学学报:信息科学版, 2015, 40(2): 193-198 (Deng Liansheng, Jiang Weiping, Li Zhao, et al. Analysis of Higher-Order Ionospheric Effects on Reference Frame Realization and Coordinate Variations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 193-198)
(  0) 0) |
| [9] |
朱春春, 李征航, 屈小川, 等. 高阶电离层延迟对GPS双差观测值和基线向量的影响[J]. 大地测量与地球动力学, 2015, 35(1): 81-86 (Zhu Chunchun, Li Zhenghang, Qu Xiaochuan, et al. Higher-Order Ionospheric Effects on the GPS Double Difference Observation and Baseline Vectors[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 81-86)
(  0) 0) |
| [10] |
姜卫平, 李昭, 邓连生, 等. 高阶电离层延迟对GPS坐标时间序列的影响分析[J]. 科学通报, 2014, 59(10): 913-92 (Jiang Weiping, Li Zhao, Deng Liansheng, et al. Impact of Higher Order Ionospheric Delay on Continuous GPS Coordinate Time Series[J]. Chinese Science Bulletin, 2014, 59(10): 913-92)
(  0) 0) |
| [11] |
Petrie E J, Hernández-Pajares M, Spalla P, et al. A Review of Higher Order Ionospheric Refraction Effects on Dual Frequency GPS[J]. Surveys in Geophysics, 2011, 32(3): 197-253 DOI:10.1007/s10712-010-9105-z
(  0) 0) |
| [12] |
Alizadeh M M, Wijaya D D, Hobiger T, et al. Ionospheric Effects on Microwave Signals[A]//Böhm J, Schuh H. Atmospheric Effects in Space Geodesy[M]. Berlin Heidelberg: Springer, 2013
(  0) 0) |
| [13] |
Elsobeiey M, El-Rabbany A. On Modelling of Second-Order Ionospheric Delay for GPS Precise Point Positioning[J]. The Journal of Navigation, 2012, 65(1): 59-72 DOI:10.1017/S0373463311000531
(  0) 0) |
| [14] |
Hernandez-Pajares M, Juan J M, Sanz J, et al. Second-Order Ionospheric Term in GPS: Implementation and Impact on Geodetic Estimates[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B8)
(  0) 0) |
| [15] |
Hoque M M, Jakowski N. Higher Order Ionospheric Propagation Effects on GPS Radio Occultation Signals[J]. Advances in Space Research, 2010, 46(2): 162-173 DOI:10.1016/j.asr.2010.02.013
(  0) 0) |
| [16] |
刘西凤, 袁运斌. 我国中低纬地区GPS定位中的电离层二阶项延迟影响分析与研究[J]. 中国科学:物理学力学天文学, 2010, 40(5): 658-662 (Liu Xifeng, Yuan Yunbin. Preliminary Analysis on the Effect of Second-Order Ionospheric Delay on GPS Positioning Solution over the Mid-Low Latitude Regions in China[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2010, 40(5): 658-662)
(  0) 0) |
| [17] |
Elmas Z G, Aquino M, Marques H A, et al. Higher Order Ionospheric Effects in GNSS Positioning in the European Region[J]. Annales Geophysicae, 2011, 29(8): 1383-1399 DOI:10.5194/angeo-29-1383-2011
(  0) 0) |
| [18] |
Bassiri S, Hajj G A. Higher-Order Ionospheric Effects on the Global Positioning System Observables and Means of Modeling Them[J]. Manuscripta Geodaetica, 1993, 18(5): 280-280
(  0) 0) |
| [19] |
Fritsche M, Dietrich R, Knöfel C, et al. Impact of Higher-Order Ionospheric Terms on GPS Estimates[J]. Geophysical Research Letters, 2005, 32(23)
(  0) 0) |
| [20] |
张小红, 任晓东, 郭斐. 顾及电离层延迟高阶项改正的精密单点定位[J]. 武汉大学学报:信息科学版, 2013(8): 883-887 (Zhang Xiaohong, Ren Xiaodong, Guo Fei. Influence of Higher-Order Ionospheric Delay Correction on Static Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2013(8): 883-887)
(  0) 0) |
| [21] |
Marques H A, Monico J F G, Aquino M. RINEX_HO: Second-and Third-Order Ionospheric Corrections for RINEX Observation Files[J]. GPS Solutions, 2011, 15(3): 305-314 DOI:10.1007/s10291-011-0220-1
(  0) 0) |
| [22] |
Dach R, Lutz S, Walser P, et al. Bernese GNSS Software Version 5.2[Z]. 2015
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


