近年来,我国大部分地区遭遇高浓度PM2.5。PM2.5的主要成分多为挥发性或半挥发性,易受气候环境的影响。例如,硫化物的含量会随着温度升高而增加,半挥发物质如硝酸盐和有机碳受到温度的影响会在颗粒物和气态之间转化,云层增加会增加硫化物的含量,相对湿度的增加会促进硝酸铵的形成和PM水汽[1-2]含量的增加。
事实上,PM2.5在污染严重地区对大气温度存在两种影响[3-4]:一种是硫酸盐含量过高,会增加地气系统反照率,减少地气系统的能量输入,从而对气候系统起到冷却作用;另一种是吸收性颗粒物的存在,吸收太阳辐射,使得到达地面的太阳辐射减少量是大气顶层的3倍,从而降低地表温度[5]。这两种影响见图 1,数据来自于编号为54511的探空站实际观测,相应PM2.5浓度数据来自北京监测中心(http://www.bjmemc.com.cn)。

|
图 1 PM2.5在污染区域对大气温度的影响 Fig. 1 The influence of PM2.5 on atmospheric temperature during polluted regions |
本文利用北京地区的探空资料研究PM2.5对地表温度的影响,并估计其在GPS气象中对加权平均温度的影响。
1 将大气垂直温度变化投影到地表温度图 2的PM2.5浓度2014~2015年数据来自万柳(WL)、西直门北(XZMB)和丰台花园(FTHY)监测站。54511号探空站位于该3个站的中心,其2005~2016年观测数据由美国怀明俄大学提供。

|
图 2 2014年和2015年PM2.5浓度变化 Fig. 2 The dense variation of PM2.5 in the year of 2014 and 2015 |
PM2.5对大气的影响与行星边界层高度有关。本文利用探空站温度廓线数据发现,PM2.5对温度廓线的影响大概分为4类:第1类为大气温度不受PM2.5浓度的影响,见图 3(a);第2类为PM2.5对下层大气温度产生冷效果,见图 3(b);第3类为PM2.5对太阳辐射具有吸收性影响,见图 3(c);最后一类是PM2.5不仅对太阳辐射具有吸收性影响,还能改变上层大气的结构,见图 3(d)。受影响的行星边界分别为0 km、0 km、1.6 km、1.5 km。

|
图 3 PM2.5对大气温度影响的4种情形 Fig. 3 The influence of PM2.5 on temperature |
假使大气温度廓线不受PM2.5浓度的影响,那么温度随高度的增加呈现线性递减。本文根据这个原理,提出利用不受PM2.5影响的上层温度廓线来计算地表温度。其物理含义为,将上层大气温度的变化投影到地表温度上,通过地表温度来反映上层大气温度的变化情况以及地表温度受环境影响的程度。首先确定区间,即确定对流层顶和不受PM2.5浓度影响的大气行星边界高度。对2015-01共31 d的温度廓线进行分析,采用对流层顶高10 km、大气行星边界高0.8 km。确定区间后,采用最小二乘原理对温度进行拟合(见图 3)。显然,受到PM2.5浓度影响的标准差基本是未受到PM2.5浓度影响的2倍。
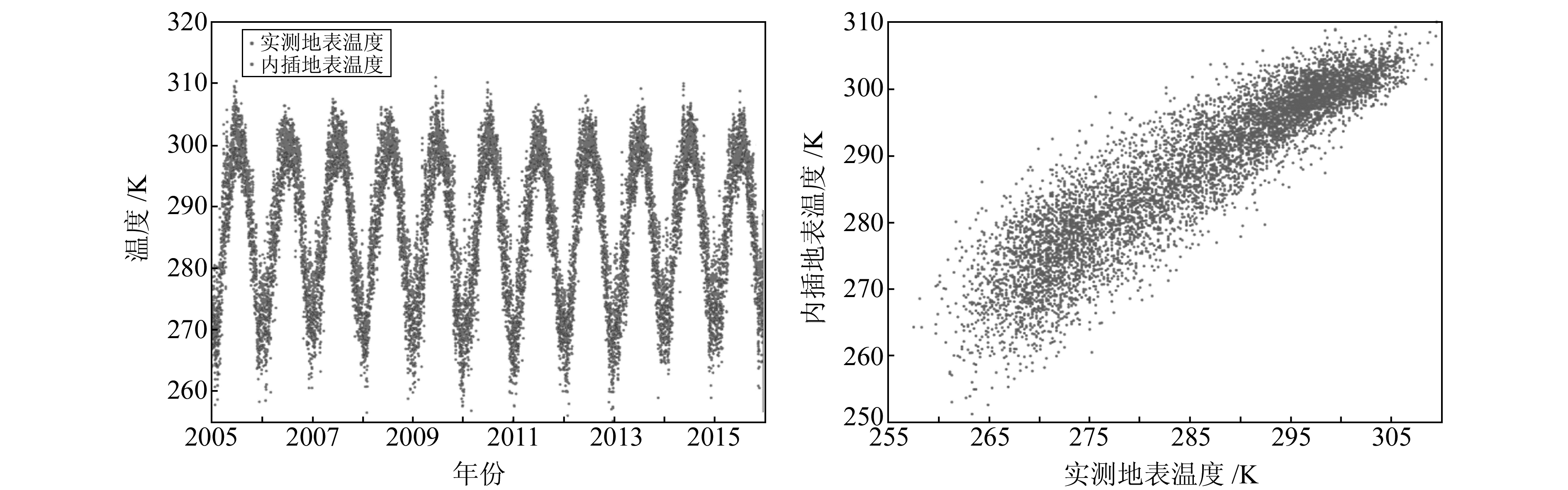
1.2 外插地表温度与实测地表温度之间的统计特性本文利用2005~2015年探空资料,根据上节确定的高度区间,利用线性最小二乘原理回归分析温度与高度的关系,计算外插地表温度(extrapolated surface temperature,EST),并与探空站实测地表温度(measured surface temperature,MST)进行比较。图 4(a)为外插地表温度和实测地表温度随时间的变化,它们随时间具有良好的周期性,外插地表温度在冬季和春季波动比较大,在夏季较为集中。图 4(b)为外插地表温度与实测地表温度的差值变化。很明显,这种差值具有季节性,在夏季最小、冬春两季最大。外插地表温度整体要高于实测地表温度,平均值为2.43 K,标准差为4.67 K,两者相关性达0.92。
|
图 4 外插地表温度与实测地表温度 Fig. 4 Extrapolated and measured surface temperature |
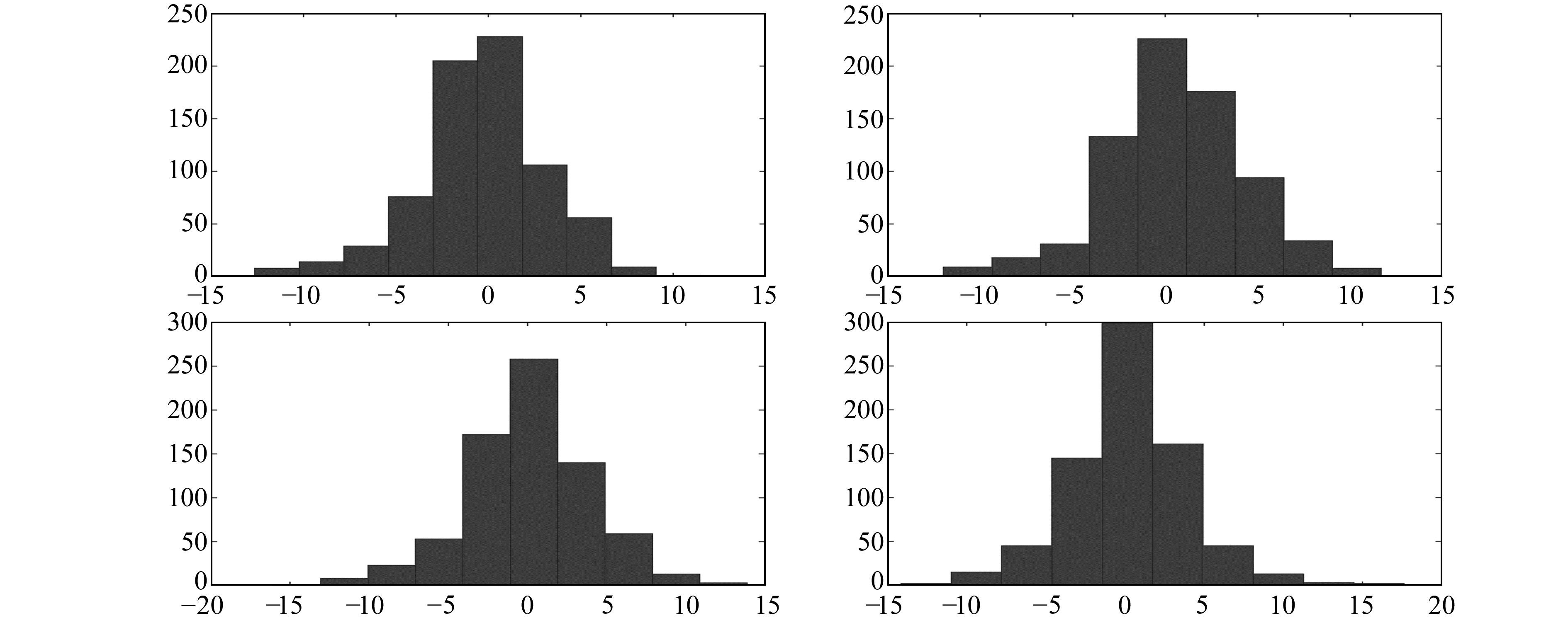
图 5为2012~2015年外插地表温度与实测地表温度差值的直方图。2012年和2013年的直方图极端值较多,0值的频率在235左右。2014年和2015年的直方图有极端值出现,但频率较低,0值的频率在2014年突破250,2015年达到300。以上差异的变化说明,外插地表温度与实测地表温度受到PM2.5浓度的影响,两者的差异开始缩小。2005~2015年,实测地表温度与外插地表温度的平均值和标准差分别为285.7 K、288.1 K、286.1 K、288.8 K和11.7 K、11.4 K、11.23 K、10.33 K。显然,2005年与2015年相比,由于受到PM2.5影响,实测地表温度提高0.4 K,外插地表温度提高0.7 K,方差分别降低0.47 K和1.07 K。
|
图 5 外插地表温度与实测地表温度差值直方图 Fig. 5 The histogram of two different temperature |
本节将讨论外插地表温度与实测地表温度对加权平均温度的影响。加权平均温度真值Tmtrue是根据探空站观测数据求得的,其定义和计算由文献[6]给出。实际上,加权平均温度与多种影响因子有关,如地表温度、温度递减率、对流层顶等[7]。由于加权平均温度与地表温度具有强烈的线性相关性,本文利用Bevis线性公式来探讨它们的影响:
| $ T_{\mathrm{m}}=a \cdot T_{{\rm s}}+b $ | (1) |
式中,a、b为待拟合系数。
模型均方根误差RMSE为:
| $ \operatorname{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(T_{\text { mtrue }i}-T_{\mathrm{m}i}\right)^{2}}{n}} $ | (2) |
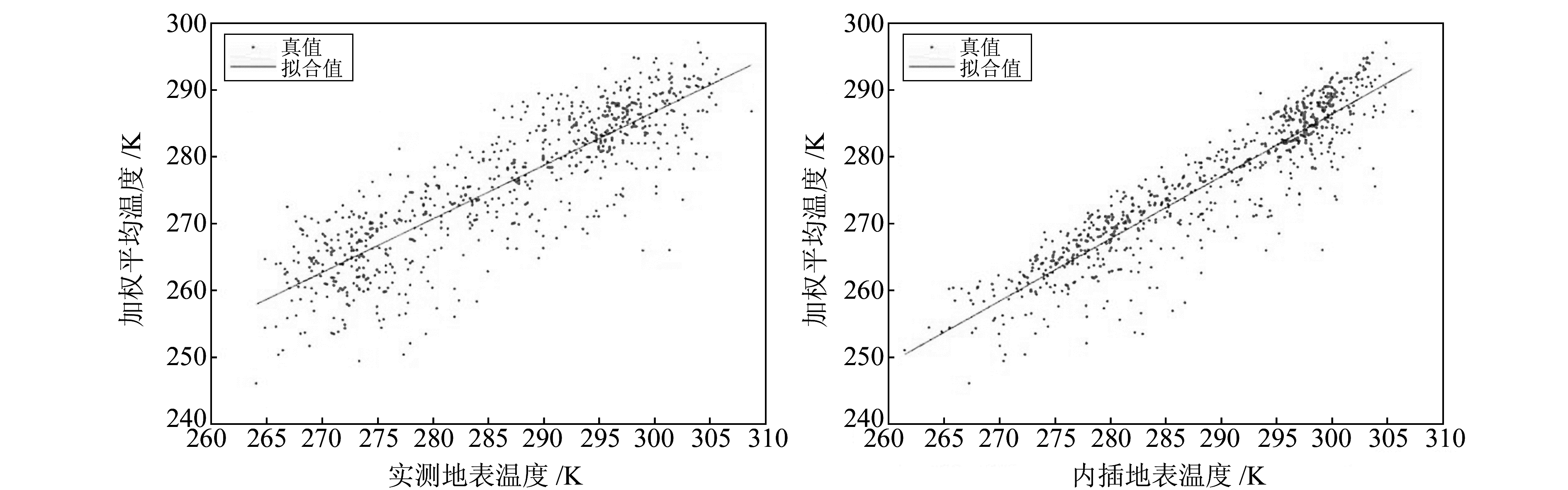
利用两种地表温度对2015年加权平均温度进行拟合,结果见图 6和表 1。从图 6可以发现,加权平均温度与外插地表温度的分布更为聚集,其拟合标准差从5.6 K降低到4.2 K, 决定系数提高0.12。
|
图 6 加权平均温度与两种地表温度的拟合情况 Fig. 6 The fitting results of weighted mean temperature |
|
|
表 1 两种地表温度的拟合情况 Tab. 1 The fitting results of two different temperature |
继续利用2010~2014年数据对式(1)进行拟合,其标准差分别见表 2。显然,利用外插地表温度可以获得更好的拟合结果,使得模型标准差下降1.2~1.7 K左右,效果明显。
|
|
表 2 2010~2014年拟合标准差 Tab. 2 RMSE of every year in 2010-2014 |
实测温度和外插温度的差值随时间的变化因人类活动的影响表现出一定的趋势性。将它们分别应用于加权平均温度,外插地表温度比实测温度所获得的加权平均温度模型有更好的效果,使得模型标准差降低1.2~1.7 K。这表明,由于人类活动和大气污染等因素的影响,地表实测温度在拟合加权平均温度时存在很大偏差,降低了它与加权平均温度之间的相关性。未来可以利用球谐函数将外插温度表达为测站位置和年积日的函数关系。
| [1] |
Jacob D J, Winner D A. Effect of Climate Change on Air Quality[J]. Atmospheric Environment, 2009, 43(1): 51-63
(  0) 0) |
| [2] |
Tai A P K, Mickley L J, Jacob D J. Correlations between Fine Particulate Matter (PM2.5) and Meteorological Variables in the United States: Implications for the Sensitivity of PM2.5, to Climate Change[J]. Atmospheric Environment, 2010, 44(32): 3976-3984 DOI:10.1016/j.atmosenv.2010.06.060
(  0) 0) |
| [3] |
Gao Y, Zhang M, Liu X, et al. Change in Diurnal Variations of Meteorological Variables Induced by Anthropogenic Aerosols over the North China Plain in Summer 2008[J]. EGU General Assembly Conference, 2016, 18: 103-118
(  0) 0) |
| [4] |
Wang J, Wang S, Jiang J, et al. Impact of Aerosol-Meteorology Interactions on Fine Particle Pollution During China's Severe Haze Episode in January 2013[J]. Environmental Research Letters, 2013, 9(9): 094002
(  0) 0) |
| [5] |
夏祥鳌, 王明星. 气溶胶吸收及气候效应研究的新进展[J]. 地球科学进展, 2004, 19(4): 630-635 (Xia Xiang'ao, Wang Mingxing. Atmospheric Science:A Vigorous Frontier Science[J]. Advances in Earth Science, 2004, 19(4): 630-635 DOI:10.3321/j.issn:1001-8166.2004.04.021)
(  0) 0) |
| [6] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology-Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Global Engineering Education Conference, 1992, 59: 844-846
(  0) 0) |
| [7] |
Liu J H, Yao Y B. A New Weighted Mean Temperature Model in China[J]. Advance in Space, 2018, 61: 402-412 DOI:10.1016/j.asr.2017.09.023
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


