2. 湖南科技大学资源环境与安全工程学院,湖南省湘潭市桃园路,411201;
3. 山东省气象局,济南市无影山路12号,250031;
4. 江苏省气象科学研究所,南京市昆仑路16号,210009
由GPS技术可以得到对流层总延迟(ZTD),ZTD减去干延迟(ZHD)可得到湿延迟(ZWD),ZWD可通过相应公式推算得到大气可降水量(GPS-PWV)[1-4]。计算ZHD要用到测站处地面大气压(P),ZWD与PWV之间的转换系数也要用到加权平均温度(Tm)、地面温度(Ts)及P等参数,Tm的精度直接影响PWV的精度[5-6]。诸多学者在利用Tm推算PWV方面进行研究[7-10],但用到的参数越多,计算过程也越复杂,数据量大、效率不高且易产生误差累积,因此一些学者尝试建立ZTD与PWV的直接转换模型。于胜杰等[11]利用北京、武汉、乌鲁木齐、拉萨、昆明等5个测站2003~2005年无线电探空数据推导PWV与ZTD之间的线性关系,获得偏差较小的PWV;王勇等[12]利用2005年武汉地区GPS气象网数据推导由ZTD直接计算PWV的模型,并对模型结果进行检验,证明两者具有很好的相关性;张胜凯等[13]利用2010年黄河站及其周边9个IGS站分析影响PWV的3个因素,验证ZTD直接转换PWV的可靠性。
本文利用2015年郴州CORS站GPS及并址探空站数据,采用线性回归和最小二乘法建立PWV与ZTD、Ts及P之间直接转换模型,并将几种转换模型得到的PWV分别与RS-PWV和GPS-PWV进行比较,验证其精度和可靠性。
1 PWV与ZTD、气象参数的相关性 1.1 数据来源及方法本文利用2015年湖南郴州CORS站得到的GPS-ZTD,减去ZHD得到ZWD进而推算GPS-PWV,并与并址的RS-PWV及温度(T)、P和相对湿度(RH)等气象数据进行模型建立和精度分析(图 1)。用2015年上半年RS-PWV进行建模,以2015年下半年RS-PWV作为真值进行模型精度的检验。
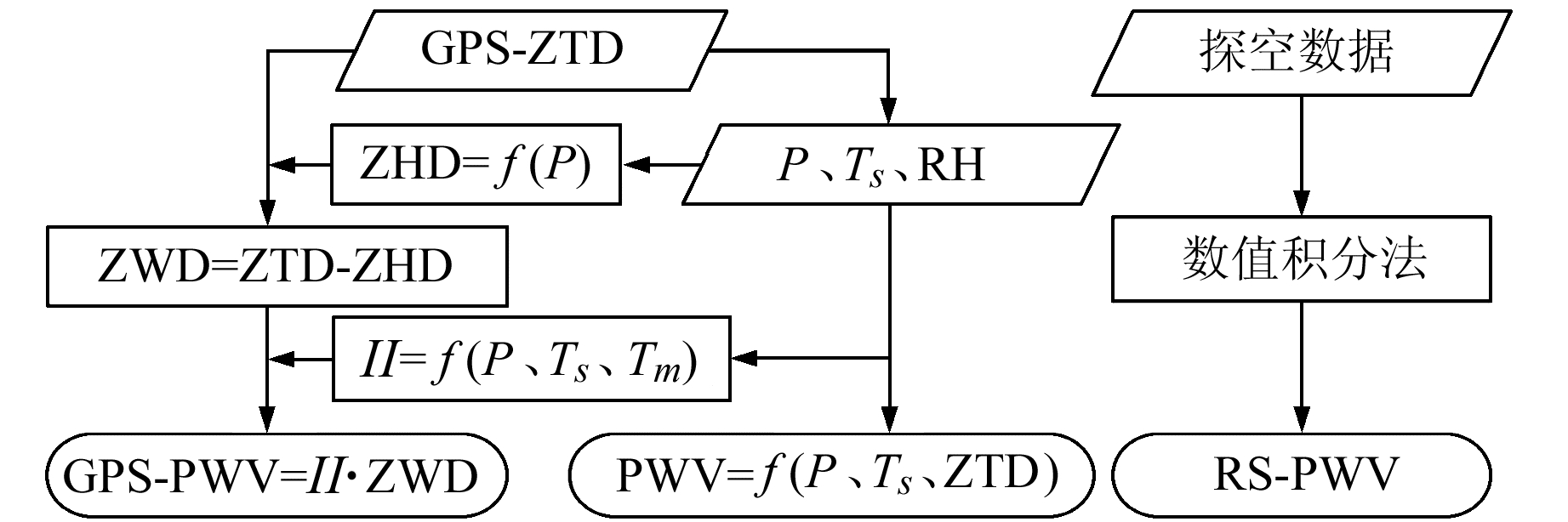
|
图 1 3种PWV的计算流程 Fig. 1 The calculational flowchart of three PWVs |
计算PWV过程中产生误差的主要因素有ZWD、T和P等参数[11-12]。由图 1可知,ZTD和ZWD之间的转换误差主要由ZHD引起,ZHD主要受P影响,因此PWV与ZTD之间的转换需要考虑T、P等的影响。本文对PWV与ZTD、T、P等气象参数的相关性进行分析,并根据其相关性强弱建立PWV直接转换模型。图 2给出2015年湖南郴州站RS-PWV与GPS-ZTD之间的线性关系。可以看出,RS-PWV与GPS-ZTD之间有很强的线性相关性,相关系数达到0.927 6。

|
图 2 RS-PWV和GPS-ZTD的相关性 Fig. 2 Relationship between RS-PWV and GPS-ZTD |
图 3(a)中,PWV与1阶温度的相关系数为0.602 1,相关性较强。图 3(b)~图 3(f)为PWV与多阶拟合温度的相关性分析,可以看出,随着阶数的增加,二者相关性有所增强。4阶拟合温度与PWV的相关系数提高到0.640 1,而5阶后的相关性与4阶接近,提高幅度不大。

|
图 3 PWV和多阶拟合温度的相关性 Fig. 3 Relationship between PWV and multi-order fitting temperature |
由图 4(a)可知,P与PWV之间的相关系数为-0.626 3,与4阶拟合温度的相关系数相近,可考虑将P加入直接转换模型。由图 4(b)可知,PWV与RH之间的相关系数仅有-0.003,RH的影响可忽略不计,不必纳入转换模型。
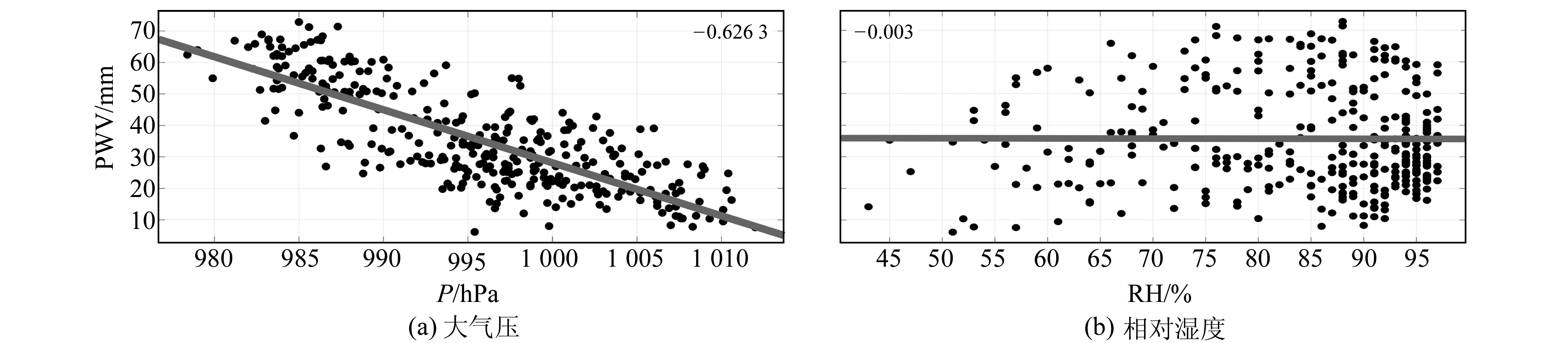
|
图 4 PWV和大气压、相对湿度之间的相关性 Fig. 4 The relationship between PWV, pressure and relative humidity |
综上可知,RS-PWV与GPS-ZTD之间线性相关性最强,可以建立PWV与ZTD之间的单因子直接转换模型;T与P也对PWV具有较大的影响,可加入到直接转换模型中建立关于ZTD、T与P的多因子PWV直接转换模型。
2 PWV直接转换模型建立与分析 2.1 模型建立方法由相关性分析可知,PWV与ZTD、T和P之间存在较强的相关性,采取多元线性拟合方法建立ZTD、T和P的单阶3因子直接转换模型:
| $ \mathrm{PWV}=a \cdot \mathrm{ZTD}+b \cdot T+c \cdot P+d $ | (1) |
其中,a、b、c为各参数的对应系数,d为常数项,所有参数可通过最小二乘原理得到。
由于PWV与ZTD的相关系数达0.927 6, 可建立PWV与ZTD的单阶单因子直接转换模型:
| $ \mathrm{PWV}=a \cdot \mathrm{ZTD}+b $ | (2) |
在式(2)中加入多阶温度项,可建立关于ZTD和4阶拟合温度的多阶多因子直接转换模型:
| $ \mathrm{PWV}=a \cdot \mathrm{ZTD}+b_{i} \cdot \sum\limits_{i=1}^{4} T^{n}+c $ | (3) |
将2015年上半年的湖南郴州CORS站GPS-ZTD数据与RS-PWV数据及对应的Ts、P分别引入以上公式,建立3种转换模型,结果见表 1。
|
|
表 1 3种转换模型 Tab. 1 Three fitting models |
将单阶单因子直接转换模型PWV、RS-PWV和GPS-PWV进行比较,给出3种PWV分布趋势和偏差。由图 5(a)可知,三者变化趋势一致。图 5(b)为三者之间的偏差图,以RS-PWV为真值,与GPS-PWV的相关系数为0.960 3,与直接转换模型PWV的相关系数为0.927 6,直接转换模型PWV与GPS-PWV的相关系数达0.969 9,说明ZTD可直接建立转换模型推算PWV,证明了ZTD单阶单因子转换模型的可行性。

|
图 5 ZTD推算PWV、GPS-PWV和RS-PWV的对比分析 Fig. 5 Contrastive analysis of ZTD-obtained PWV, GPS-PWV and RS-PWV |
将3种转换模型计算的PWV分别与RS-PWV进行比较,验证3种模型的精度和可靠性。图 6为3种模型的变化趋势与偏差。可以看出,3种模型的趋势走向基本一致,偏差基本集中于-10~10 mm,大部分在-5~5 mm。

|
图 6 3种模型PWV对比分析 Fig. 6 Contrastive analysis of three models' PWV |
表 2给出3种模型的精度统计结果。可以看出,加入T和P的单阶多因子模型比单阶单因子模型精度有明显提高,RMS从4.3 mm提高到3.3 mm; 多阶多因子模型与单阶多因子模型相比,精度略有提高(仅0.1 mm),效果有限;将温度因子进行4阶处理后,虽相关性有所增强,但模型稳定性有所降低(平均偏差相比单阶多因子模型升高0.6),且计算量较大。目前国内PWV精度在1~3 mm就能满足要求,该模型精度虽有损失,但提高了转换效率。因此,在需要较高精度时可考虑建立多阶多因子模型,当本地有丰富气象参数时可建立单阶多因子模型。
|
|
表 2 3种模型的精度评估 Tab. 2 The accuracy assessment of three models |
1) 相关性分析表明,RS-PWV与GPS-ZTD之间存在很强的线性关系,相关系数为0.927 6;PWV与P呈负相关, 相关系数为-0.626 3; PWV与4阶拟合温度的相关系数达到0.640 1;PWV与RH的相关系数仅有-0.003。
2) 基于ZTD的单阶单因子模型PWV与GPS-PWV的相关系数达到0.969 9,说明ZTD直接推算PWV具有可行性。
3) 基于ZTD、T和P的单阶多因子PWV模型比基于ZTD的单阶单因子PWV模型精度有明显提高,RMS从4.3 mm提高到3.3 mm;基于T和ZTD的多阶多因子模型精度虽略有提高,但计算量较大。在实际应用中,当本地有丰富气象参数时可建立单阶多因子模型。
| [1] |
丁金才. GPS气象学及其应用[M]. 北京: 气象出版社, 2009 (Ding Jincai. GPS Meteorology and Its Application[M]. Beijing: Meteorology Press, 2009)
(  0) 0) |
| [2] |
李国平. 地基GPS气象学[M]. 北京: 科学出版社, 2010 (Li Guoping. Ground-Based GPS Meteorology[M]. Beijing: Science Press, 2010)
(  0) 0) |
| [3] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [4] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [5] |
Basili P, Bonafoni S, Ferrara R, et al. Atmospheric Water Vapor Retrieval by Means of Both a GPS Network and a Microwave Radiometer during an Experimental Campaign in Cagliari, Italy, in 1999[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2436-2443 DOI:10.1109/36.964980
(  0) 0) |
| [6] |
Wang X M, Zhang K F, Wu S Q, et al. Water Vapor-Weighted Mean Temperature and Its Impact on the Determination of Precipitable Water Vapor and Its Linear Trend[J]. Journal of Geophysical Research Atmospheres, 2016, 121(2): 833-852 DOI:10.1002/2015JD024181
(  0) 0) |
| [7] |
龚绍琦. 中国区域大气加权平均温度的时空变化及模型[J]. 应用气象学报, 2013, 24(3): 332-334 (Gong Shaoqi. The Spatial and Temporal Variations of Weighted Mean Atmospheric Temperature and Its Models in China[J]. Journal of Applied Meteorological Science, 2013, 24(3): 332-334 DOI:10.3969/j.issn.1001-7313.2013.03.009)
(  0) 0) |
| [8] |
张洛恺, 杨力, 王艳玲, 等. 郑州地区大气加权平均温度模型确定[J]. 测绘科学技术学报, 2014, 31(6): 566-569 (Zhang Luokai, Yang Li, Wang Yanling, et al. Modeling of Atmosphere Weighted Mean Temperature of Zhengzhou Region[J]. Journal of Geomatics Science and Technology, 2014, 31(6): 566-569 DOI:10.3969/j.issn.1673-6338.2014.06.004)
(  0) 0) |
| [9] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 412-415 (Wang Xiaoying, Dai Ziqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-415)
(  0) 0) |
| [10] |
谷晓平, 王长耀, 吴登秀. GPS水汽遥感中的大气加权平均温度的变化特征及局地算式研究[J]. 气象科学, 2005, 25(1): 79-83 (Gu Xiaoping, Wang Zhangyao, Wu Dengxiu. Research on the Local Algorithm for Weighted Atmospheric Temperature Used in GPS Remote Sensing Water Vapor[J]. Scientia Meteorologica Sinica, 2005, 25(1): 79-83 DOI:10.3969/j.issn.1009-0827.2005.01.011)
(  0) 0) |
| [11] |
于胜杰, 柳林涛. 无地面温压数据的可降水量研究[J]. 大地测量与地球动力学, 2008, 28(5): 34-38 (Yu Shengjie, Liu Lintao. Study on Precipitable Water Vapor without Meteorological Data[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 34-38)
(  0) 0) |
| [12] |
王勇, 刘严萍, 柳林涛. 区域GPS网对流层延迟直接推算可降水量研究[J]. 热带气象学报, 2007, 23(5): 510-514 (Wang Yong, Liu Yanping, Liu Lintao. The Study of Directly Calculating Precipitable Water Vapor with Zenith Tropospheric Delay of GPS Network[J]. Journal of Tropical Meteorology, 2007, 23(5): 510-514 DOI:10.3969/j.issn.1004-4965.2007.05.013)
(  0) 0) |
| [13] |
张胜凯, 赵云, 鄂栋臣. 利用GPS技术遥感北极黄河站可降水量的研究[J]. 极地研究, 2015, 27(3): 264-270 (Zhang Shengkai, Zhao Yun, E Dongchen. Precipitable Water Vapor at Arctic Yellow River Station Measured Using GPS Technology[J]. Chinese Journal of Polar Research, 2015, 27(3): 264-270)
(  0) 0) |
2. School of Resource Environment and Safety Engineering, Hunan University of Science and Technology, Taoyuan Road, Xiangtan 411201, China;
3. Shandong Meteorology Bureau, 12 Wuyingshan Road, Ji'nan 250031, China;
4. Jiangsu Institute of Meteorological Sciences, 16 Kunlun Road, Nanjing 210009, China
 2019, Vol. 39
2019, Vol. 39

