2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
大气可降水量是大气系统的重要组成部分,及时准确掌握可降水量的变化,对短期天气预报具有重要意义。GPS可降水量的时空变化复杂,且具有非线性、非平稳特征。近年来,一些学者利用神经网络方法进行GPS可降水量的预报研究。文献[1-2]利用经验模态分解与RBF神经网络相结合的方法进行GPS可降水量预报;文献[3]利用Morlet小波基代替BP神经网络中的激活函数,建立小波神经网络模型用于GPS可降水量预报,提高预报精度;文献[4]利用自适应卡尔曼滤波与RBF相结合进行GPS可降水量预报,获得良好效果。然而,神经网络具有训练时间长、泛化能力差、易陷入局部极小等缺点[5]。针对这个问题,本文研究了一种基于小波分解与遗传算法和支持向量机相结合的GPS可降水量短临预报方法。
1 算法原理 1.1 小波分解小波分解[6](WD)是进行信号时频分析和处理的理想工具。对于离散小波变换,Mallat构造了塔式分解和重构的快速算法。设原始信号为c0,小波分解式为:
| $ \left.\begin{aligned} c_{j+1} &=H c_{j} \\ d_{j+1} &=G d_{j} \end{aligned}\right\} $ | (1) |
其中,j=0,…,J,J为最大分解层数;H为低通滤波器;G为高通滤波器;cj是在分辨率为2j下的高频分量部分,称为细节分量;dj是在分辨率为2j下的低频分量部分,称为近似分量。
该方法每分解一次,细节分量和近似分量长度减半,但包含了原始信号各个频率子段的频率信息。小波分解后的信号为cJ和d1、d2、…、dJ,即c0=cJ+d1+d2+…+dJ。
在输入数据序列的相邻数据之间补一个0,使数据长度增加1倍,从而使小波变换后的信号长度保持不变。然后对分解后的信号进行重构:
| $ C_{j}=H^{*} C_{j+1}+G^{*} D_{j+1} $ | (2) |
其中,j=J-1, J-2, …, 0;H*和G*是对偶算子。
对cJ和d1、d2、…、dJ分别进行重构,重构后的信号为CJ和D1、D2、…、DJ,则:
| $ X=C_{J}+D_{1}+D_{2}+\cdots+D_{J} $ | (3) |
其中,CJ={cJ, 1, cJ, 2…}为第J层重构后的近似分量;D1={d1, 1, d1, 2…}, …, DJ={dJ, 1, dJ, 2…}为第1层到第J层重构后的细节分量。
1.2 最小二乘支持向量机支持向量机[7](SVM)在样本量较少的情况下仍具有良好的统计规律,具有鲁棒性、计算简单、理论完善等优点。最小二乘支持向量机(LSSVM)继承了SVM的基本思想,并用二次平方损失函数代替经典SVM的二次规划方法,求解速度更快[8]。
对于训练样本集D={(xk, yk)|k=1, 2, …, N}, 其中
| $ f(\boldsymbol{x})=\boldsymbol{\omega}^{\mathrm{T}} \varphi(\boldsymbol{x})+b $ | (4) |
式中,ω为权系数向量,b为偏置量,φ(x)为线性映射函数。可将输入向量映射到一个高维特征空间,使原本线性不可分的样本在核空间可分。函数估计问题的目标函数和约束条件如下:
| $ \min\limits_{\omega, b, e} J(\boldsymbol{\omega}, e)=\boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\omega}+\frac{1}{2} \gamma \sum\limits_{k=1}^{N} e_{k}^{2} $ | (5) |
| $ y_{k}=\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(x_{k}\right)+b+e_{k}, k=1, \cdots, N $ | (6) |
其中,J为损失函数;γ为正则化参数,是待定参数;e为偏差量。
式(5)为凸二次规划问题,需转化为线性方程组求解。为此,对其每条约束添加拉格朗日乘子ak,得到其对偶问题。该问题的拉格朗日函数为:
| $ \begin{array}{c}{L(\boldsymbol{\omega}, b, e, \boldsymbol{a})=J(\boldsymbol{\omega}, e)-} \\ {\sum\limits_{k=1}^{N} a_{k}\left\{\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(x_{k}\right)+b+e_{k}-y_{k}\right\}}\end{array} $ | (7) |
令∂L/∂ω=0,∂L/∂b =0,∂L/∂ek=0,∂L/∂ak=0,消去ω和e,可得:
| $ \left[ \begin{array}{cc}{0} & {\boldsymbol{E}_{v}^{\mathrm{T}}} \\ {\boldsymbol{E}_{v}^{\mathrm{T}}} & {\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}+\frac{1}{\gamma} \boldsymbol{I}}\end{array}\right] \left[ \begin{array}{l}{b} \\ {\boldsymbol{a}}\end{array}\right]=\left[ \begin{array}{l}{0} \\ {\boldsymbol{y}}\end{array}\right] $ | (8) |
其中,Ev=[1, …, 1]T;I为单位阵;a=[a1, …, aN]T;Ω=φ(xk)Tφ(xl),k, l=1, …, N;y=[y1, …, yN]T。
令核函数k(xk, xl)=φ(xk)Tφ(xl),根据式(8)求出a和b,故LSSVM回归估计函数为:
| $ y(x)=\sum\limits_{k=1}^{N} a_{k} k\left(x, x_{k}\right)+b $ | (9) |
本文选用高斯核函数:
| $ k\left(x_{k}, x_{l}\right)=\exp \left(\frac{-\left\|x_{k}-x_{l}\right\|}{2 \sigma^{2}}\right) $ | (10) |
其中,xk、xl为输入样本;σ>0为高斯核函数的带宽,为待定参数。
σ和γ对LSSVM的泛化性能至关重要。实际应用中通常采用试凑法或凭经验确定,不但耗时耗力,而且效果还可能不好。所以,本文利用遗传算法的全局寻优能力来确定σ和γ。
1.3 遗传算法利用遗传算法(GA)[9]优化LSSVM参数的步骤[10]如下。
1) 输入训练数据。
2) 种群初始化。个体编码方法采用实数编码,对LSSVM的σ2、γ进行编码。
3) 计算个体的适应度值。计算适应度目标函数,目的是寻找一组参数(γ, σ2),通过LSSVM训练使得式(11)目标函数全局最小,也就是适应度值最大。然后判断是否满足精度要求,若满足则执行步骤7),否则执行步骤4)。
| $ \left\{\begin{array}{l}{\min f\left(\gamma, \sigma^{2}\right)=\frac{1}{2 n} \sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}} \\ {\text { s.t }~~ \gamma \in\left[\gamma_{\min }, \gamma_{\max }\right], \quad \sigma^{2} \in\left[\sigma_{\min }^{2}, \sigma_{\max }^{2}\right]}\end{array}\right. $ | (11) |
其中yi和
4) 选择。筛选适应度优良的个体遗传给下一代,以提高全局收敛性和计算速率。
5) 交叉。随机选择第k个染色体αk和第l个染色体αl在j位的基因进行交换,产生新的优秀个体:
| $ \left.\begin{aligned} \alpha_{k j} &=\alpha_{k j}(1-\beta)+\alpha_{l j} \beta \\ \alpha_{l j} &=\alpha_{l j}(1-\beta)+\alpha_{k j} \beta \end{aligned}\right\} $ | (12) |
式中,αkj为第k个染色体在j位的基因;αlj为第l个染色体在j位的基因;β∈[0, 1]。
6) 变异。从种群中任意选取第i个个体的第j个染色体变异为更加优秀的个体:
| $ \alpha_{i j}=\left\{\begin{array}{l}{\alpha_{i j}+\left(\alpha_{i j}-\alpha_{\max }\right) f(g), r \geqslant 0.5} \\ {\alpha_{i j}+\left(\alpha_{\min }-\alpha_{i j}\right) f(g), r<0.5}\end{array}\right. $ | (13) |
式中,αmax和αmin分别是基因αij取值的上界和下界;f(g)=r(1-g/Gmax)2,g为当前迭代次数,Gmax为最大进化数,r是[0, 1]间的随机数。
7) 终止循环,得到最佳染色体。将遗传算法优化得到的最优个体分解为σ2和γ,用于预报。
2 基于WD-GA-LSSVM的可降水量短临预报结合WD、GA和LSSVM的优点,利用WD-GA-LSSVM方法进行可降水量预报,步骤如下。
1) 把GPS可降水量的原始时间序列x(t)通过小波分解得到1个近似分量cj和i个细节分量d1、d2、…、di。
2) 对分解后的各分量分别进行LSSVM建模,并利用遗传算法优化其参数,得到各分量的预报值。本文设置遗传算法的参数为:迭代次数100,种群规模20,交叉概率0.9,变异概率0.2。
3) 对各分量的预报值进行叠加重构,得到可降水量的最终预报结果。
3 实验分析为方便比较,分别设计3种方案:方案1为遗传小波神经网络模型(GA-WNN),方案2为LSSVM模型,方案3为WD-GA-LSSVM模型。
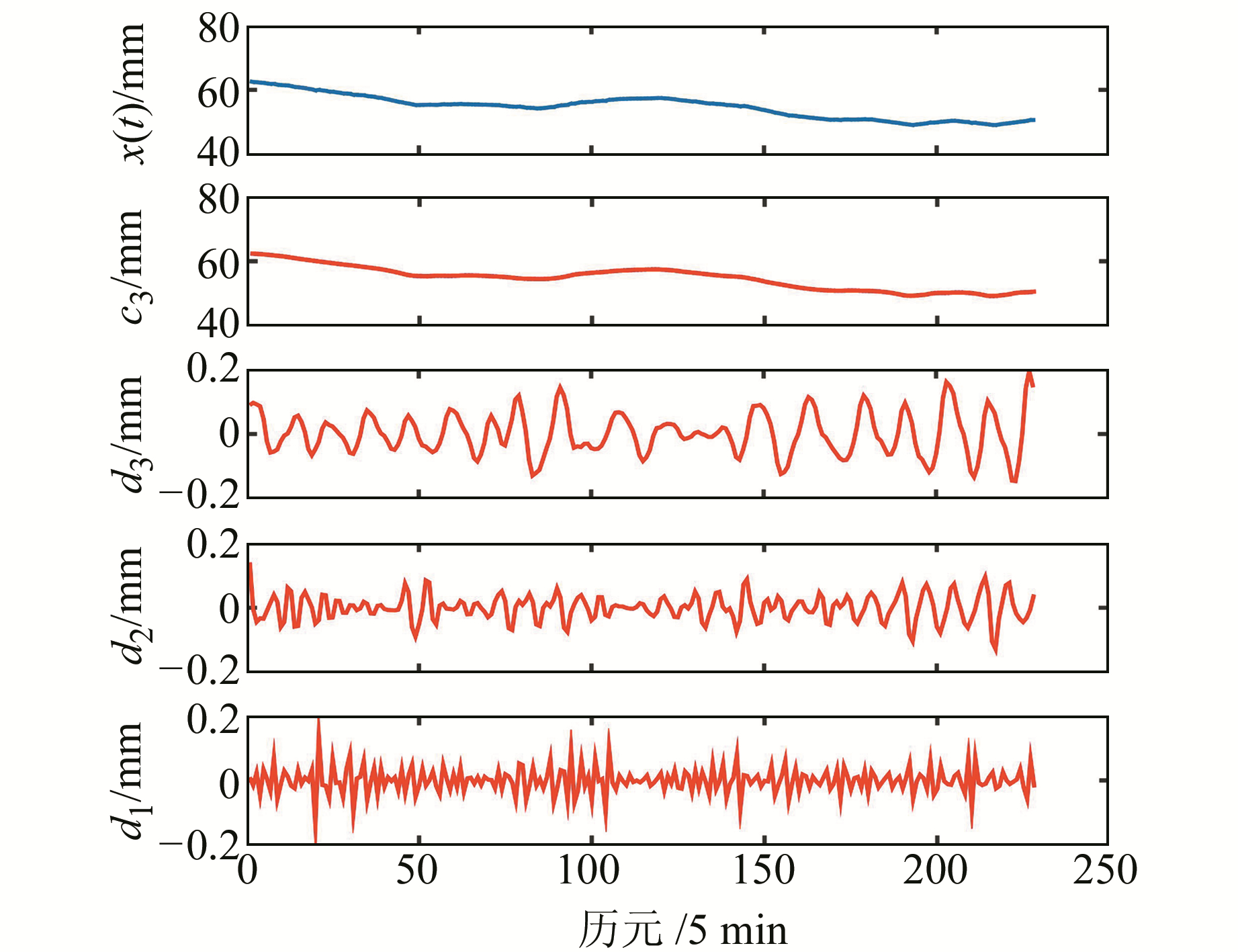
选取武汉站2016-07-04 GPS可降水量数据进行分析。该天年积日为186 d,天气为暴雨转大雨。该站可降水量数据利用GAMIT 10.6软件解算出对流层延迟,再结合气象数据计算获得。数据采样率为5 min,共228个历元数据,选用前192个为输入样本,后36个为测试样本。采用db4小波基对GPS可降水量时间序列进行3级分解,原始时间序列及小波分解结果如图 1所示,其中的低频近似分量c3代表了GPS可降水量的大致变化趋势;高频细节分量d1、d2、d3的频率逐次递减,有利于对各分量进行预报。
|
图 1 年积日186 d时间序列及其小波分解结果 Fig. 1 The time series of doy 186 and its decomposition results |
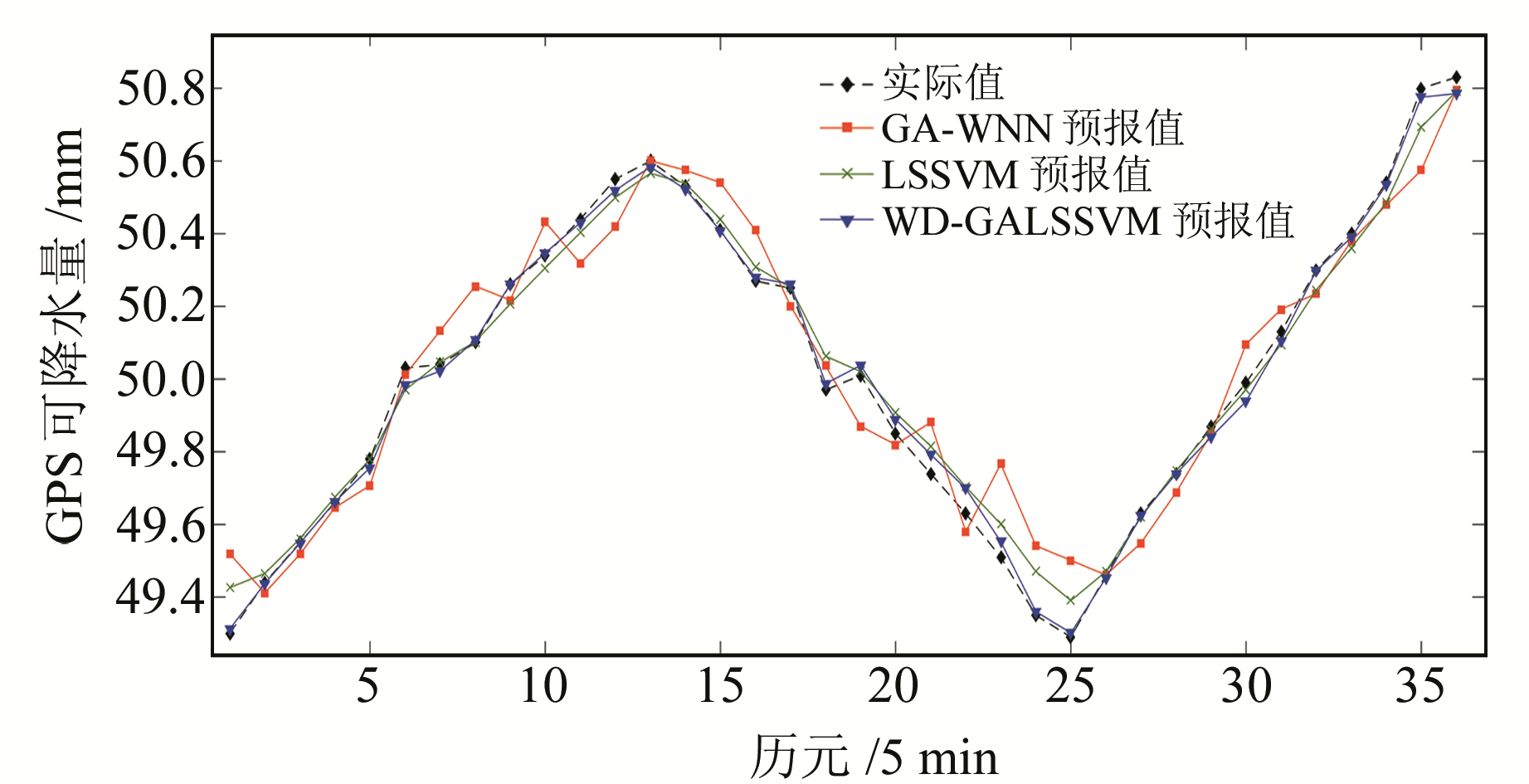
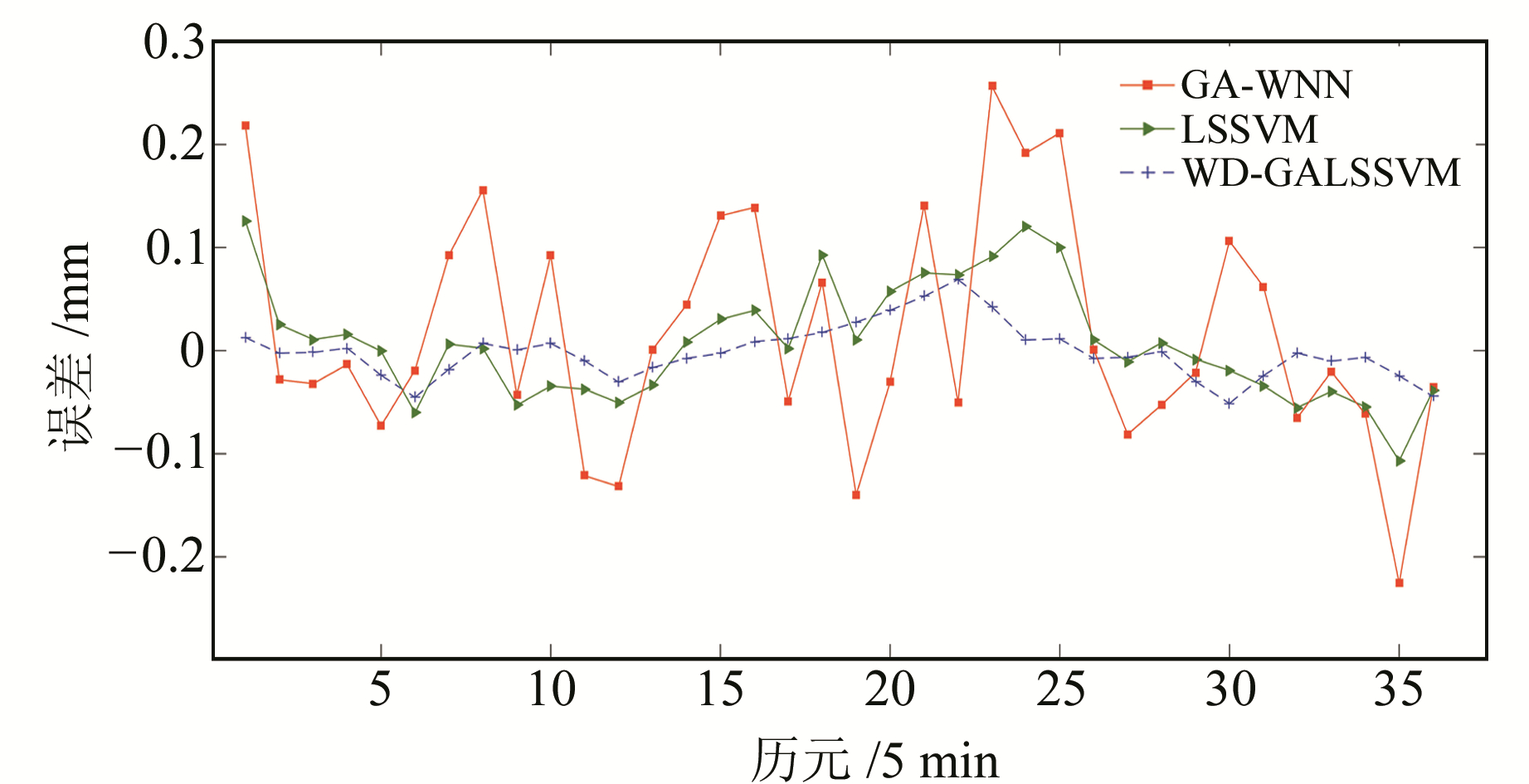
对分解后的各分量建立GA-LSSVM模型进行预报,然后重构合成预报结果。各分量参数设置见表 1,各模型预报结果如图 2,图 3为各模型预报残差对比。
|
|
表 1 年积日186 d各分量参数设置 Tab. 1 Parameter settings of each component for doy 186 |
|
图 2 年积日186 d各模型预报值和实际值对比 Fig. 2 Comparison between the predicted values of each model and the actual value for doy 186 |
|
图 3 年积日186 d各模型残差 Fig. 3 Residual of each model for doy 186 |
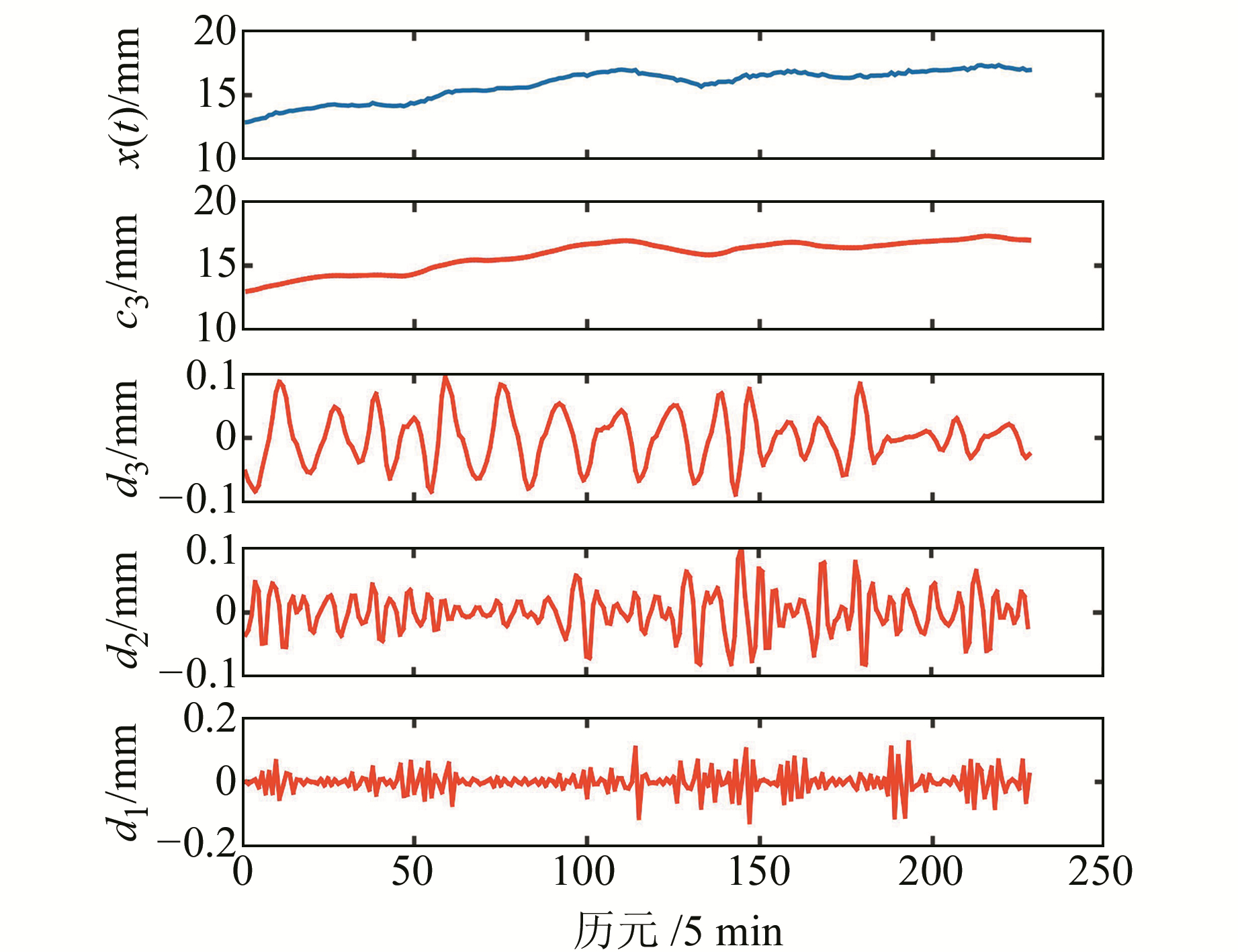
为进一步验证该算法的效果,选取北京房山站2016-11-20的GPS可降水量数据进行分析。该天年积日为325 d,天气为雨夹雪转大雪,采样率为5 min, 共228个历元数据。选用前192个历元数据为输入样本,后36个为测试样本,选用db4小波基对GPS可降水量时间序列进行3级分解,结果如图 4。
|
图 4 年积日325 d时间序列及其小波分解结果 Fig. 4 The time series of doy 325 and its decomposition results |
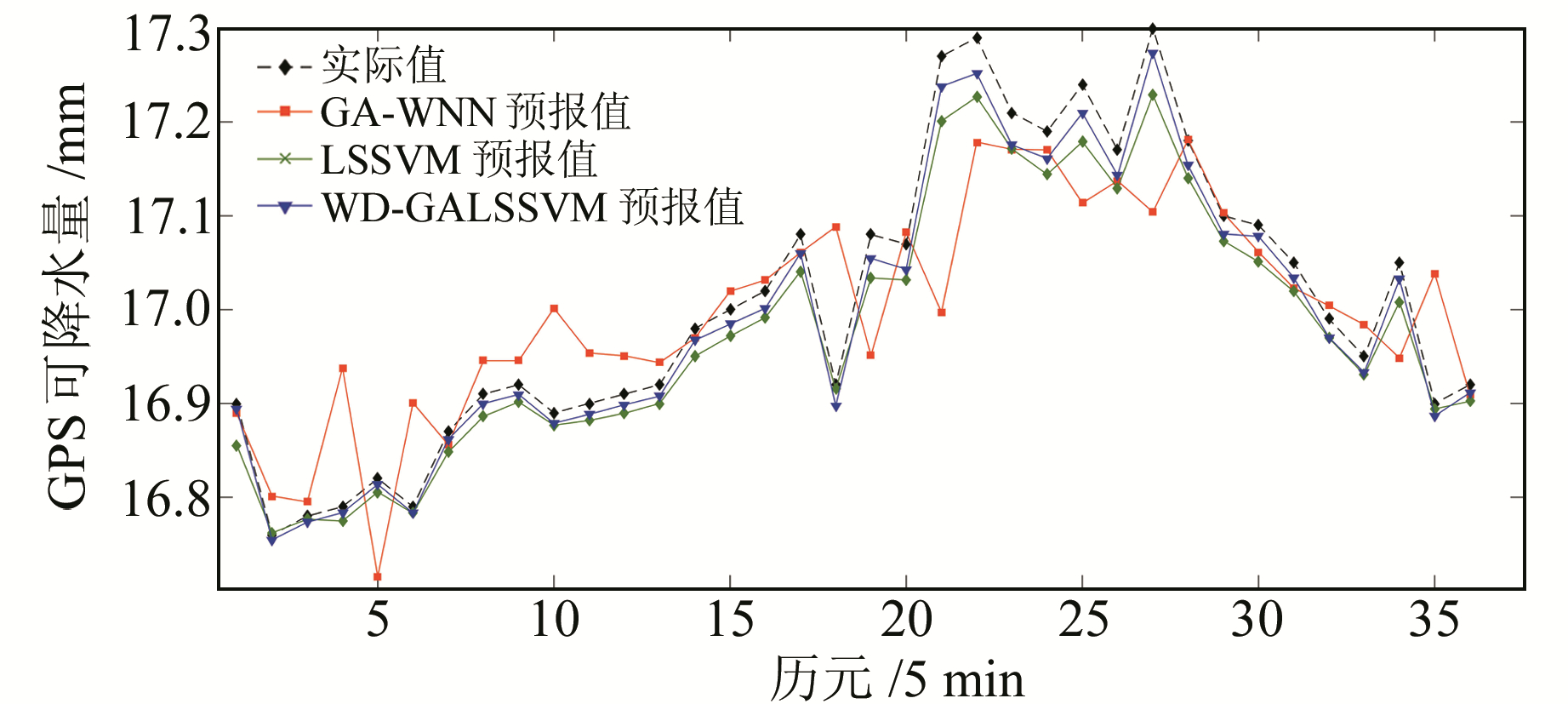
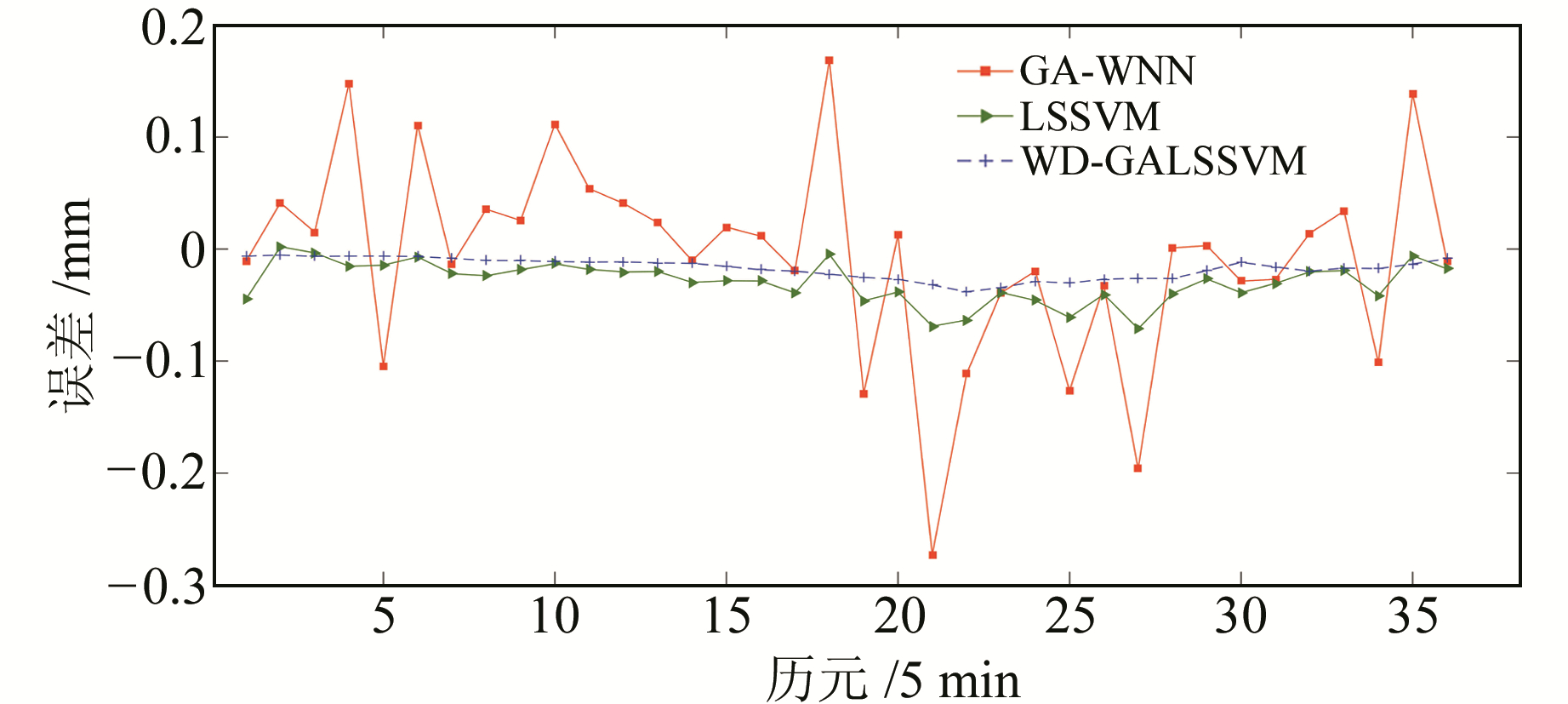
对分解后的各分量建立GA-LSSVM模型进行预报,然后重构合成预报结果。各分量参数设置见表 2,预报结果如图 5、图 6所示,两组数据各模型的均方根误差(RMSE)及平均绝对误差(MAE)见表 3(单位mm)。
|
|
表 2 年积日325 d各分量参数设置 Tab. 2 Parameter settings of each component for doy 325 |
|
图 5 年积日325 d各模型预报值和实际值对比 Fig. 5 Comparison between the predicted values of each model and the actual value for doy 325 |
|
图 6 年积日325 d各模型残差 Fig. 6 Residual of each model for doy 325 |
|
|
表 3 各模型精度对比 Tab. 3 Comparison of the accuracy of each model |
由图 2和图 5可以看出,方案3的预报结果更接近实际,结果更加稳定;由图 3和图 6可知,方案3的残差变化最小,预报效果最好;由表 3可知,方案3的RMSE和MAE指标也显著优于另外两种方案,进一步证明该方法的优越性。表 3结果还显示,方案2的预报精度也明显优于方案1,表明该方法能有效解决神经网络的一些缺陷。
4 结语本文研究了基于小波分解、遗传算法和LSSVM的GPS可降水量预报方法,利用不同季节、不同天气的GPS可降水量时间序列对其性能进行验证,并与遗传小波神经网络、LSSVM方法进行比较。结果表明,LSSVM方法显著优于遗传小波神经网络方法,WD-GA-LSSVM方法的预报精度比LSSVM方法也有明显提高,为短临天气预报提供了一种新的思路。
| [1] |
刘严萍, 杨晶, 王勇. 经验模态分解与神经网络的GPS可降水量预测[J]. 测绘科学, 2013, 38(5): 91-93 (Liu Yanping, Yang Jing, Wang Yong. Prediction of GPS Water Vapor Based on EMD and ANN[J]. Science of Surveying and Mapping, 2013, 38(5): 91-93)
(  0) 0) |
| [2] |
张朝菡.基于EMD与RBF的GPS可降水量的降水预报研究[D].唐山: 河北联合大学, 2015 (Zhang Zhaohan. Research on Precipitation Forecast of GPS Precipitable Water Vapor Based on EMD and RBF[D]. Tangshan: Hebei United University, 2015) http://cdmd.cnki.com.cn/Article/CDMD-10081-1015808436.htm
(  0) 0) |
| [3] |
葛玉辉, 熊永良, 陈志胜, 等. 基于小波神经网络的GPS可降水量预测研究[J]. 测绘科学, 2015, 40(9): 28-32 (Ge Yuhui, Xiong Yongliang, Chen Zhisheng, et al. Prediction Method of GPS Precipitation Based on Wavelet Neural Network[J]. Science of Surveying and Mapping, 2015, 40(9): 28-32)
(  0) 0) |
| [4] |
王建敏, 黄佳鹏, 席克伟, 等. 大气可降水量预测模型的自适应Kalmam滤波改进[J]. 测绘科学, 2017, 42(12): 127-133 (Wang Jianmin, Huang Jiapeng, Xi Kewei, et al. Improved Prediction Model of Precipitable Water Vapor Using Adaptive Kalman Filter[J]. Science of Surveying and Mapping, 2017, 42(12): 127-133)
(  0) 0) |
| [5] |
杨锡运, 孙宝君, 张新房, 等. 基于相似数据的支持向量机短期风速预测仿真研究[J]. 中国电机工程学报, 2012, 32(4): 35-41 (Yang Xiyun, Sun Baojun, Zhang Xinfang, et al. Short-Term Wind Speed Forecasting Based on Support Vector Machine with Similar Data[J]. Proceedings of the CSEE, 2012, 32(4): 35-41)
(  0) 0) |
| [6] |
王晓兰, 王明伟. 基于小波分解和最小二乘支持向量机的短期风速预测[J]. 电网技术, 2010, 34(1): 179-184 (Wang Xiaolan, Wang Mingwei. Short-Term Wind Speed Forecasting Based on Wavelet Decomposition[J]. Power System Technology, 2010, 34(1): 179-184)
(  0) 0) |
| [7] |
朱家元, 陈开陶, 张恒喜. 最小二乘支持向量机算法研究[J]. 计算机科学, 2003, 30(7): 157-159 (Zhu Jiayuan, Chen Kaitao, Zhang Hengxi. Study of Least Squares Support Vector Machines[J]. Computer Science, 2003, 30(7): 157-159 DOI:10.3969/j.issn.1002-137X.2003.07.044)
(  0) 0) |
| [8] |
阎威武, 邵惠鹤. 支持向量机和最小二乘支持向量机的比较及应用研究[J]. 控制与决策, 2003, 18(3): 358-360 (Yan Weiwu, Shao Huihe. Application of Support Vector Machines and Least Squares Support Vector Machines to Heart Disease Diagnoses[J]. Control and Decision, 2003, 18(3): 358-360 DOI:10.3321/j.issn:1001-0920.2003.03.025)
(  0) 0) |
| [9] |
鲁凤, 徐建华, 王占永. 合肥市需水预测遗传小波神经网络模型研究[J]. 测绘科学, 2013, 38(5): 28-31 (Lu Feng, Xu Jianhua, Wang Zhanyong. Model of Genetic Algorithms Optimized Wavelet Neural Network on Urban Water Demand Prediction of Hefei[J]. Science of Surveying and Mapping, 2013, 38(5): 28-31)
(  0) 0) |
| [10] |
王小川. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013 (Wang Xiaochuan. Analysis of 43 Cases of MATLAB Neural Network[M]. Beijing: Beihang University Press, 2013)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2019, Vol. 39
2019, Vol. 39

