2. 中国地震局地球物理研究所,北京市民族大学南路5号,100081;
3. 广东省地震局,广州市先烈中路81号,510070;
4. 中国地震局地震观测技术研究院,北京市民族大学南路5号,100081
地震观测记录是多种地动信号叠加的结果[1],对观测记录中的地震信号进行分析,并区分和比较地震信号及地动噪声,是地震学研究非常重要的内容。地震信号可以近似为一个复杂的位移阶跃信号或速度脉冲信号[2],其谐波分量幅度及相位遵循一定的数学关系,原则上是平滑的频率函数。地震信号归为暂态信号,具有有限的能量和零功率,分为脉冲型和振荡型两类,通常使用能量谱密度(ESD)描述其频谱分布特征[1]。地动噪声由各类信号叠加产生,其相位谱具有不确定性[1]。地动噪声可以近似为平稳随机过程,归为稳态信号,具有无限能量和有限功率,主要包含随机噪声和单色正弦信号两类,通常使用功率谱密度(PSD)进行描述。因此,用于表征地震信号以及地动噪声的物理量存在不兼容的现象。
1 地震信号与地动噪声的RMS表征为了能在统一尺度上表达地震信号与地动噪声,Aki[3]提出暂态信号的小波f(t)在t=0附近的峰值振幅可以由“振幅谱密度”和小波频带宽度的乘积近似表示,而稳态信号则用其PSD来表征。Fix等[4-5]按照1/3倍频程频带宽度从PSD计算出相应的RMS。在定义频带宽度下,脉冲信号的峰值幅度与频带宽度成比例,噪声幅度大致与频带宽度的平方根成比例。这样,地震信号与地动噪声就可以在RMS下进行统一比较。
计算RMS值的方法有两种:一种是在一定频带上以一定的倍频程频带宽度对时域波形进行带通滤波,然后根据RMS定义直接计算RMS;另一种是先计算PSD,对观测系统通频带内一定频带宽度上的PSD值进行积分,得到观测系统输出端功率,再对功率开方得到对应频带宽度上的RMS。理论上,这两种方法得到的RMS值应该具有很高的一致性,然而由于窄带滤波器参数和PSD计算参数配置的差异,两种方法计算的RMS值存在一定差异。针对该问题,本文使用两种方法分别计算RMS值,给出1/3倍频程频带宽度下的窄带滤波器优化设计参数,列出PSD值反算RMS值的参数最优区间,分别对两种方式获得的RMS值进行误差概率分析。
2 仿真数据合成为了对计算结果的误差进行定量分析,本文合成1 000个波形ST(i),每个波形由1 126条正弦子波Ssub(i, j)合成,子波的频率从0.5 Hz到23 Hz以0.02 Hz为步长变化,每个子波的幅度和时间延迟由计算机随机产生。合成1 000个波形是为了增加误差概率分析时的样本数,分析在样本数达到多少时结果趋于稳定。
| $ \begin{array}{l} {S_{{\rm{sub}}}}\left( {i, j} \right) = A\left( {i, j} \right) \times \\ \sin \left( {2\pi f\left( j \right)t + {\Delta _t}\left( {i, j} \right)} \right) \end{array} $ | (1) |
式中,i=1, 2…, 1 000为波形编号,j=1, 2…, 1 126为子波编号;t为采样时间序列,从0.01以0.01为步长增加到T(i); T(i)为波形时间长度,从100以10为步长增加到1 090;A(i, j)为子波幅度;Δt(i, j)为波形延迟;
把合成的1 000个不同长度的波形在0.89~22.4 Hz的频带内按照1/3倍频程分为14个子频带,对于每个波形,将落入14个子频带内的子波分别叠加,形成14个子频带合成波形Ssub-T(i, k):
| $ {S_{{\rm{sub}}-{\rm{T}}}}\left( {i, k} \right) = \sum\limits_{j = {N_{k-l}}}^{{N_{k-h}}} {{S_{{\rm{sub}}}}\left( {i, j} \right)} $ | (2) |
式中,i=1, 2…, 1 000为波形编号,k=1,…14为子频带编号,Nk-l为第k个子频带下限频率在1 126个子波中的编号,Nk-h为第k个子频带上限频率在1 126个子波中的编号。根据RMS值的定义,使用Ssub-T(i, k)直接计算的RMS值RMSR(i, k)作为第i个合成波形ST(i)在第k个子频带上RMS值的基准值,用于后面的相对误差计算,R表示参考基准。
3.1 滤波后计算RMS值根据每个子频带的上下限频率设计FIR型窗口函数带通滤波器,其频率响应特性主要依赖于滤波器阶数和窗口函数类型,滤波特性随着滤波器阶数的提高而更加接近理想状态[6]。
在计算每个子频带RMS值时,对滤波器的窗口函数及阶数进行变化,其中每个带通滤波器的窗口函数有16种,滤波器阶数从2以步长1增加到1 000,再从1 020以步长20增加到5 000。
RMSmnk-NF(m, i, n, k)为使用FIR滤波器对ST(i)滤波后,使用每个波形后50 s数据计算得到的RMS值,m为滤波器窗口函数的编号,i为波形编号,n为滤波器阶数, k为子频带编号, NF表示窄带滤波器。
针对每个固定的窗口函数,将RMSmnk-NF(m, i, n, k)与RMSR(i, k)进行比较,得到两者之间的误差比:
| $ \begin{array}{l} {\rm{RM}}{{\rm{S}}_{\_{\rm{error}}\_{\rm{ratio}}}}(m, i, n, k) = \\ \frac{{{\rm{RM}}{{\rm{S}}_{mnk-{\rm{NF}}}}(m, i, n, k)-{\rm{RM}}{{\rm{S}}_R}(i, k)}}{{{\rm{RM}}{{\rm{S}}_R}(i, k)}} \times 100 \end{array} $ | (3) |
在固定的窗口函数下对RMS_error_ratio(m, i, n, k)进行概率统计,得到每个滤波器阶数上的RMS_error_ratio(m, i, n, k)的概率分布结果RMS_error_ratio_probility(m, n),在参与计算的合成波形达到100条后趋于稳定,细化结果表现为以hann和rectwin为代表的两类窗口函数。
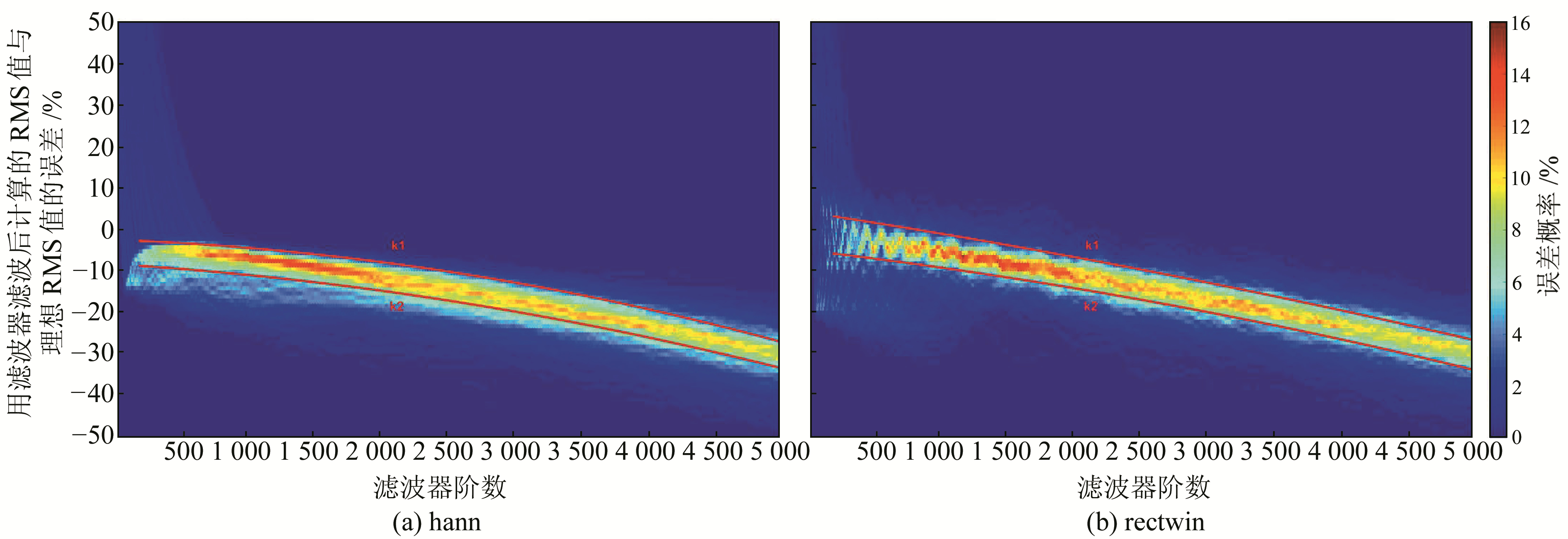
从图 1可以看出,使用hann窗口函数的滤波器对原始波形进行滤波后,再计算得到的RMS值与参考RMS值的误差主要集中在由k1和k2控制的狭长条带区间内。该条带整体随滤波器阶数的增加呈下降趋势,集中误差分布由最初的-4%~-9%,在k1和k2控制下逐渐集中到-27%~-33%。使用rectwin窗口函数时,RMS值的误差在低于800阶时存在振荡,在800阶以后误差主要集中在由k1和k2控制的狭长条带区间,该条带随滤波器阶数的增加整体呈下降趋势,集中误差分布由最初的3%~-5%,在k1和k2控制下逐渐集中到-25%~-33%。
|
图 1 使用不同阶数的hann及rectwin窗口函数滤波器滤波后计算的RMS值误差概率统计 Fig. 1 The error probability statistics for the RMS calculated after filtered with FIR filter designed in hann and rectwin window with different orders |
在使用FIR窗口函数方法设计带通滤波器计算RMS值的过程中,滤波器的窗口函数类型和阶数是影响计算结果误差分布的主要因素。从计算结果可以看出,不同窗口函数类型的结果在低于1 000阶时有一定差别,误差概率分布形态基本趋势相同,误差主要集中在由k1和k2控制的狭长条带区间内,该条带在k1和k2的夹持下整体随滤波器阶数的增加呈现下降趋势,意味着随着滤波器阶数的上升带来滤波器特性的改变,引入的滤波器响应使得误差会以逐渐放大的趋势集中。图 2显示,使用500阶左右的turkeywin窗口函数,或是370阶至880阶的kaiser和rectwin窗口函数所计算的RMS值误差在±5%以内的概率为50%左右。在其他窗口函数下,结果误差在±5%以内的概率则在30%以下。

|
图 2 使用16种滤波器窗口函数在不同滤波器阶数下对波形滤波后计算的RMS值误差在±1%及±5%以内的概率统计 Fig. 2 Theprobability statistics for the error within ±1% and ±5% of RMS calculated after filtered with filter designed in 16 different windows with different orders |
采用Welch平均周期图法[7]计算PSD时,有几个常用参数,如窗口函数类型、窗口长度、分段数据长度及相邻数据段的重叠率, 这些参数的配置直接影响信号谱及平方相干函数的计算结果。研究[7]显示,信号谱的计算精度与分段数据长度呈反比,为平衡谱计算精度与相干系数方差及偏差的矛盾,通常采用相邻数据段部分数据重叠的方法。在分段数据长度固定的情况下,重叠率与滑动步长呈反比。随着分段数据长度[8]和重叠率的增大[9],谱计算的方差会降低,不同数据段互相关性及稳定性会增加,但是相应的计算量也会增大。Carter[10]指出,在固定窗口长度时,当重叠率达到一定程度后,数据段互相关性及稳定性会达到一个相对恒定的状态。
通过变换窗口函数类型、窗口长度、重叠率等3个参数计算PSD并进一步计算RMS值,其中窗口长度与分段数据长度相等,按1/3倍频程的相对频带宽度在0.89~22.4 Hz频段确立中心频点,对14个子频带内的PSD值分别进行积分、开方,并用这个值来表征该子频带的RMS值,表示为PSD2RMS_imjgk。把每个ST(i)在相同窗口函数类型、窗口长度、重叠率下得到的PSD2RMS_imjgk与对应的RMSR(i, k)进行比较,统计误差在±1%及±5%以内的概率,分别表示为PSD2RMS_mjg_1和PSD2RMS_mjg_5。
PSDRMS_imjgk是由PSD反算的RMS值,其中i表示波形编号,m表示滤波器的窗口函数类型编号,j代表窗口长度占原数据长度的百分比,g代表相邻两段数据的重叠率,k代表子频带编号。
| $ {\rm{PS}}{{\rm{D}}_{2{\rm{RMS}}\_ijk\_1}} = \frac{{N\_{\rm{PS}}{{\rm{D}}_{2{\rm{RMS}}\_mjg\_1}}}}{{N\_{\rm{PS}}{{\rm{D}}_{2{\rm{RMS}}\_mjg\_{\rm{T}}}}}} $ | (4) |
| $ {\rm{PS}}{{\rm{D}}_{2{\rm{RMS}}\_ijk\_5}} = \frac{{N\_{\rm{PS}}{{\rm{D}}_{2{\rm{RMS}}\_mjg\_5}}}}{{N\_{\rm{PS}}{{\rm{D}}_{2{\rm{RMS}}\_mjg\_{\rm{T}}}}}} $ | (5) |
式中,N_PSD2RMS_mjg_1为误差在±1%以内的个数,N_PSD2RMS_mjg_5为误差在±5%以内的个数,N_PSD2RMS_mjg_T为参与统计的总数,该值等于参与统计的ST(i)个数乘以14。
针对每个窗口函数在不同窗口长度及重叠率组合下得到的PSD2RMS_mjg_1和PSD2RMS_mjg_5进行分析发现,这两个固定误差阀值的概率分布大致可以分为两类:一类是以flattopwin窗口函数为代表,在合成的ST(i)达到20条后,RMS值误差±5%以内的概率统计结果进入稳定状态,达到400条后RMS值误差±1%以内的概率统计结果进入稳定状态(图 3);另一类是以turkeywin窗口函数为代表的其余15个,在合成的ST(i)达到120条后,RMS值误差±5%以内的概率统计结果进入稳定状态,达到150条后RMS值误差±1%以内的概率统计结果进入稳定状态(图 4)。

|
图 3 应用flattopwin窗口函数在不同窗口长度和重叠率参数组合下计算的PSD反算RMS值误差±1%及±5%以内的概率统计 Fig. 3 The probability statistics for the error within ±1% and ±5% of RMS calculated from PSD calculated with different window length and different overlap ratio under flattopwin window |

|
图 4 应用turkeywin窗口函数在不同窗口长度和重叠率参数组合下计算的PSD反算RMS值误差±1%及±5%以内的概率统计 Fig. 4 The probability statistics for the error within ±1% and ±5% of RMS calculated from PSD calculated with different window length and different overlap ratio under turkeywin window |
结果显示,在每一个窗口函数类型下,±1%和±5%的误差概率分布较为集中,基本呈条带和块状。高概率主要分布在窗口长度3%~14%、重叠率在中高比例的区间,受窗口长度的影响多于受重叠率的影响。说明在一定的窗口长度下,随着重叠率的增加,相邻数据段间互相关性及稳定性提高,谱估计的方差降低并趋于稳定,RMS值计算结果符合设定误差范围的概率就高,且分布区域较为连续。
4 结语在使用FIR窗口函数方法设计带通滤波器计算RMS值的过程中,滤波器的窗口函数类型和阶数是影响计算结果误差的2个主要因素,其中滤波器阶数作用更大。在滤波器窗口函数固定的情况下,RMS_error_ratio_probility(m, n)主要集中在由k1和k2控制的狭长条带区间内,该条带随着滤波器阶数的增加整体呈下降趋势,意味着随着滤波器阶数的上升,误差会以逐渐放大的趋势在概率分布上集中。通过对比,推荐使用500阶左右的turkeywin窗口函数,或是370~880阶的kaiser和rectwin窗口函数,这样获得的RMS有50%以上的概率误差在±5%以内。
使用pwelch函数,通过变换窗口函数类型、窗口长度、重叠率等3个参数计算PSD并进一步计算RMS值,在合成的ST(i)达到400条后,RMS值误差±1%及±5%以内概率统计结果的量级及展布形态全部进入稳定。结果还显示,在每一个窗口函数类型下,计算结果的误差受窗口长度的影响多于受重叠率的影响,误差概率总体呈现随窗口长度增加而降低的趋势。误差概率分布较为集中,基本呈条带和块状。推荐使用turkeywin窗口函数,在窗口长度3%~13%、重叠率23%~98%的近似长条区间内,误差±5%以内的概率在95%以上。在其他窗口函数类型下,在窗口长度3%~14%、重叠率的中高比例阶段在呈条带或块状的区间也有误差±5%以内概率95%以上的集中出现,但是相对turkeywin要小。
从同等误差水平的概率分布来看,使用pwelch函数,选取恰当的窗口函数类型、窗口长度、重叠率等3个参数计算PSD,并进一步计算RMS值的方法优于使用FIR设计带通滤波器对波形滤波以计算RMS值的方法。
本文在计算RMS值时,为了能定性及定量分析计算误差,使用了合成地动噪声,与自然界的地动噪声存在一定的差异。而直接使用天然地动噪声又无法建立RMS值的基准,导致无法对计算误差进行有效分析,需要找到一个平衡点来解决这个矛盾。
致谢: 感谢中国地震局地球物理研究所为该研究提供实验设备、场地及技术支持。
| [1] |
Bormann P. New Manual of Seismological Observatory Practice [R]. 2002
(  0) 0) |
| [2] |
Aki K, Richards P G. Quantitative Seismology[M]. Sausalito: University Science Books, 2002
(  0) 0) |
| [3] |
Aki K, Richards P G. Quantitative Seismology-Theory and Methods[M]. Freeman and Company, 1980
(  0) 0) |
| [4] |
Fix J E. Ambient Earth Motion in the Period Range from 0.1 to 2 560 sec[J]. Bull Seism Soc Am, 1972, 62: 1753-1760
(  0) 0) |
| [5] |
Melton B S. The Sensitivity and Dynamic Range of Inertial Seismographs[J]. Rev Geophys Space Phys, 1978, 14: 393-116
(  0) 0) |
| [6] |
Milivojevic Z.Digital Filter Design[EB/OL]. https://learn.mikroe.com/ebooks/digitalfilter
(  0) 0) |
| [7] |
Welch P D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms[J]. IEEE Trans Audio Electroacoust, 1967, AU-15: 70-73
(  0) 0) |
| [8] |
Oppenheim A V, Schafer R W. Digital Signal Processing[M]. New Jersey: Prentice-Hall Press, 1975
(  0) 0) |
| [9] |
Ringler A T, Hutt C R, Evans J R, et al. A Comparison of Seismic Instrument Noise Coherence Analysis Techniques[J]. Bull Seismol Soc Am, 2011, 101: 558-567 DOI:10.1785/0120100182
(  0) 0) |
| [10] |
Carter G C, Knapp C H, Nuttall AH. Estimation of the Magnitude-Squared Coherence Function via Overlapped Fast Fourier Transform Processing[J]. IEEE Transactions Audio and Electroacoustics, 1973, AU-21(4): 337-344
(  0) 0) |
2. Institute of Geophysics, CEA, 5 South-Minzudaxue Road, Beijing 100081, China;
3. Guangdong Earthquake Agency, 81 Mid-Xianlie Road, Guangzhou 510070, China;
4. E-Institute of Earthquake Observation Technology, 5 South-Minzudaxue Road, Beijing 100081, China
 2019, Vol. 39
2019, Vol. 39


