2. 中国科学院大学,北京市玉泉路19号甲,100049
高精度重力测量是地球科学、资源勘测等领域的研究基础[1-2]。与常规的机械式重力仪相比,超导重力仪具有极宽的动态线性测量范围、极低的噪声、极小的漂移和极高的稳定性及灵敏度[3-4],目前在各类观测地球重力场的仪器中精度最高[5]。超导重力仪利用超导电磁悬浮系统进行实时重力测量,通过2个超导线圈中持续电流产生的磁场,使超导球悬浮在一个固定的位置。当重力发生变化时,超导球将在垂直方向上产生一定的位移[6],将重力的测量转化为电压的测量。超导重力仪数据采集系统提供的重力场原始数据是以电压变化形式给出的[7-8]。超导重力仪的测量精度受磁悬浮系统倾斜的影响[9],极小的倾角会引起很大的误差,因此要实现高精度重力测量,必须对磁悬浮系统偏离水平方向的倾角进行测量和调平。
本文利用超导重力仪测量精度与磁悬浮系统倾角及支撑腿调节高度之间的关系,制作支撑腿调平系统并进行调平实验,为超导重力仪的调平工作和高精度重力测量提供参考。
1 重力精度与倾角及支撑腿之间的关系 1.1 重力精度与倾角的关系超导重力仪的测量精度受其磁悬浮系统偏离水平方向倾角的影响,当存在倾角θ时,测量的重力值g会减少到g×cosθ,与真实重力值的偏差为:
| $ \Delta g = g\left( {1 - \cos \theta } \right) \approx \left( {1/2} \right)g{\theta ^2} $ | (1) |
据式(1)可计算出不同重力测量精度与倾角θ的关系,即θ=(2Δg/g)1/2,对应结果如表 1所示。
|
|
表 1 重力精度与倾角之间的关系 Tab. 1 The relationship between gravity and inclination |
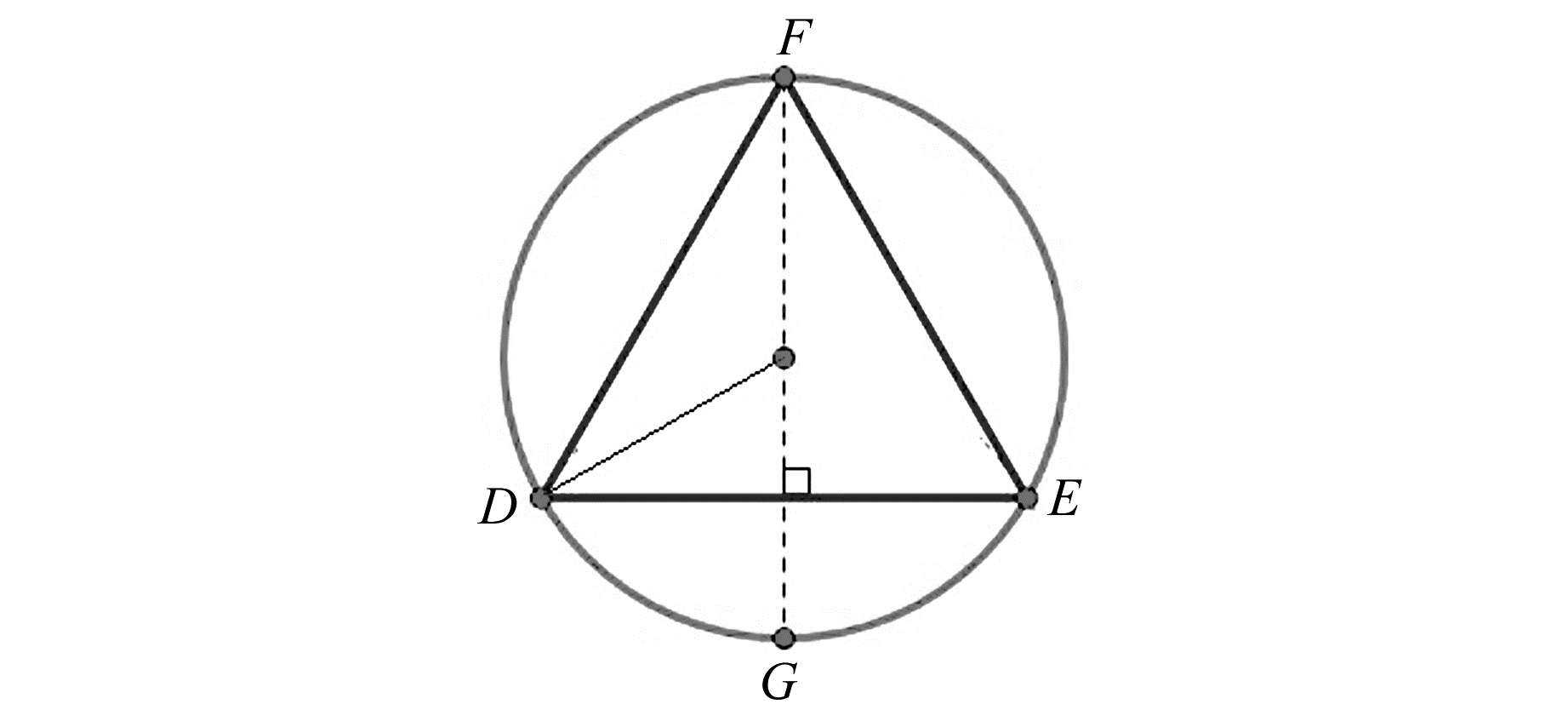
图 1为重力仪外筒和3个支撑腿位置的简化图。图中外圆为重力仪外筒,直径为500 mm,D、E、F三个点表示3个支撑脚,3点构成正三角形,可算出内接正三角形的高为:
|
图 1 重力装置外观简化图 Fig. 1 Gravity device appearance simplified diagram |
| $ h = \frac{{\sqrt 3 }}{2}DE = \frac{{\sqrt 3 }}{2} \times \sqrt 3 R = \frac{3}{2}R = 375\;{\rm{mm}} $ | (2) |
超导重力仪的调平是以其中2个脚(如D、E 2点)确定的一条线(X轴)为参考,平行放置一台电容倾角传感器,在垂直方向上(Y轴)放置另一台传感器,用以确定和调节传感器所在平面的倾角。调平时先固定D点,通过调节E点的高度使平行于X轴方向的传感器倾角为零,此时X轴方向水平,Y轴方向的倾角就是磁悬浮系统的倾角。再通过调节F点的高度使Y轴方向的传感器倾角为零,调平完成。超导重力仪的调平分为水平粗调和水平细调2个过程,此调平方法既适用于超导装置外筒的调平(粗调),也适用于磁悬浮系统的调平(细调),粗调是使2个传感器的读数为零,细调是使位移电压(反映悬浮力大小)位于峰值。
1.3 重力精度与支撑脚调节高度间的关系在调平过程中,当调节Y轴方向倾角时,设F点改变的高度为Δh,Y轴改变的倾角为Δθ,则tanΔθ=Δh/h,故有:
| $ \Delta \theta = \arctan \left( {\Delta h/h} \right) $ | (3) |
式中,h为重力仪外筒内接正三角形的高。根据表 1结果,结合h的计算值(375 mm)计算出不同重力精度与支撑脚调节高度的关系,即Δh=h×tanΔθ,结果如表 2所示。
|
|
表 2 重力精度与支撑脚高度间的关系 Tab. 2 The relationship between gravity and support feet height |
当重力仪外筒直径为500 mm时,在1 μGal精度要求下,倾角为9.14",支撑脚调节高度为16.62 μm;在0.1 μGal精度要求下,倾角为2.89",支撑脚调节高度为5.25 μm。要实现5.25 μm的高精度位移调节,并且3个支撑脚要支撑高达150 kg的重力仪是个很大的挑战。通过大量的调研发现,高精度的支撑台往往只能支撑几百g的重量,而能支撑150 kg大重量的支撑台往往体积较大且精度达不到要求。综合考虑以上要求,决定采用交流伺服电机驱动电动缸作为支撑脚。电动缸选用高精度滚珠丝杆电动缸,定位精度可达5 μm,行程30 mm;电机选用交流伺服电机,中容量中惯量,配以20位的编码器,最小调节高度为2.5 μm。此方案能同时满足支撑重量大和调节精度高的要求。
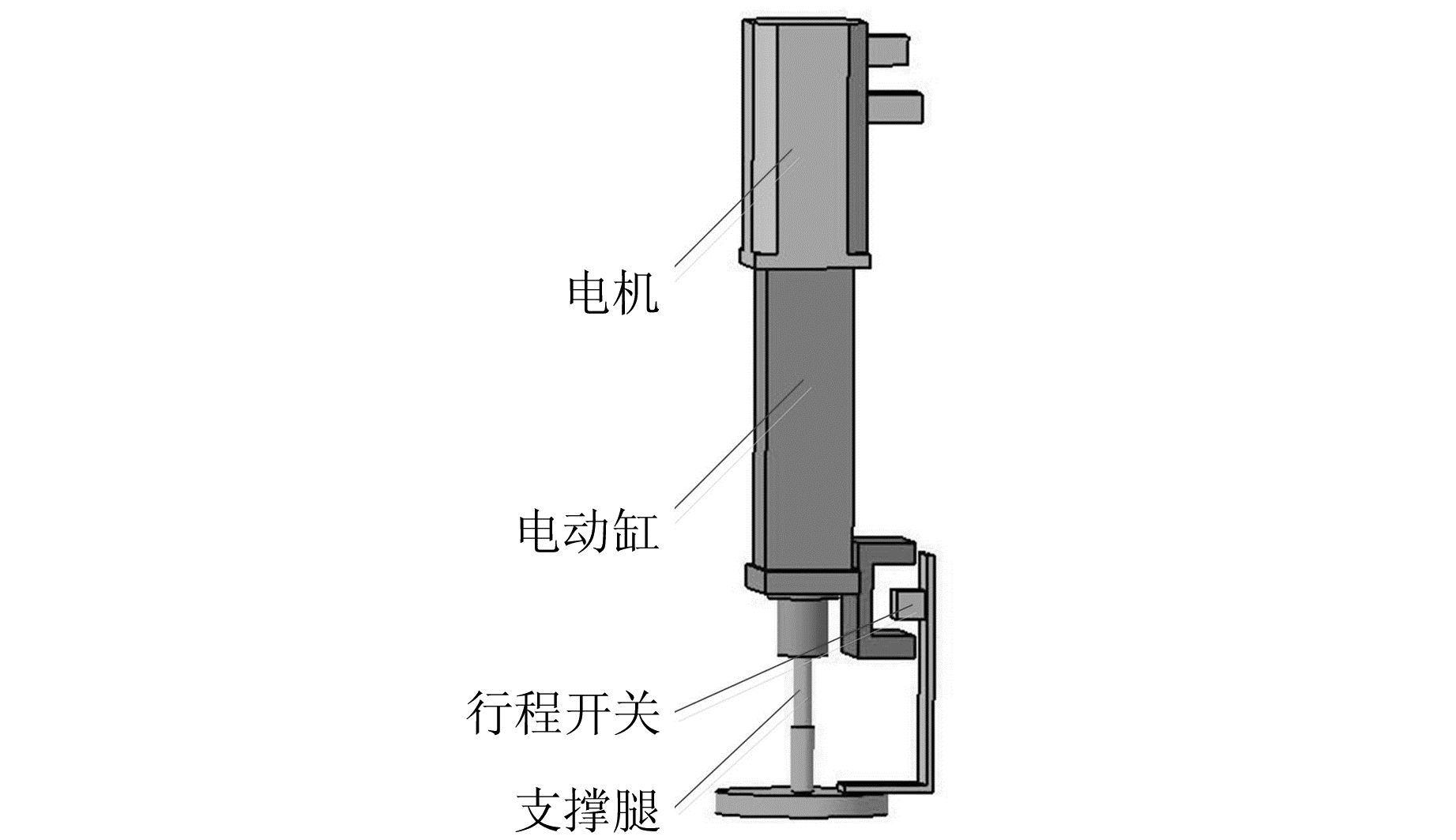
设计的重力仪自动调平系统主要由高精度倾角传感器、控制系统、电动升降支撑腿组成。控制系统主要包括触摸屏、PLC、伺服驱动器、安全限位和电气附件,能够实现人机交互、设备控制等功能。其中,触摸屏主要显示当前支撑腿的高度及水平度信息,可设置调节的角度;PLC主要与倾角传感器及伺服驱动器通信,控制伺服电机运动,达到角度和高度精细调节的目的;电动升降支撑腿由交流伺服电机和高精度电动缸组成,用于实现罐体的支撑、调平功能;高精度倾角传感器为双轴倾角传感器,安装在重力仪底部,用于采集水平度信号并反馈给控制系统。电动升降支撑腿示意图见图 2,调平系统控制框见图 3。
|
图 2 电动升降支撑腿结构示意图 Fig. 2 Electric supporting leg structure diagram |

|
图 3 调平系统控制框 Fig. 3 Leveling system control block diagram |
利用实验室的高精度数字水平仪对水平调节装置的调节精度进行评估,数字水平仪为青岛前哨精密仪器公司生产的WL11型数字水平仪,测量量程为±999",分辨率为0.1"。将数字水平仪放在待调整的平面上,然后多次改变调平装置的角度,发现在此过程中,数字水平仪测得的改变角度与调平装置改变的角度几乎一样,证明该调平装置调节的准确性,其倾角调节精度达到0.002°,按表 2重力精度与倾角关系评估,由倾斜引起的最小重力误差约为1 μGal。
3 重力仪调平实验及结果分析运用前文的调平方法进行水平粗调,然后给超导悬浮线圈通电,通过调节支撑腿使位移电压达到峰值,实现水平细调。通过调节E点高度,改变X轴方向的倾角(此过程Y轴方向倾角也会改变),找到X轴方向倾角的最小值,然后通过调节F点高度改变Y轴方向的倾角,找到新的位移电压峰值,即找到Y轴方向的最小倾角,实现水平细调。超导磁悬浮系统在此水平下进行后续的高精度重力测量。
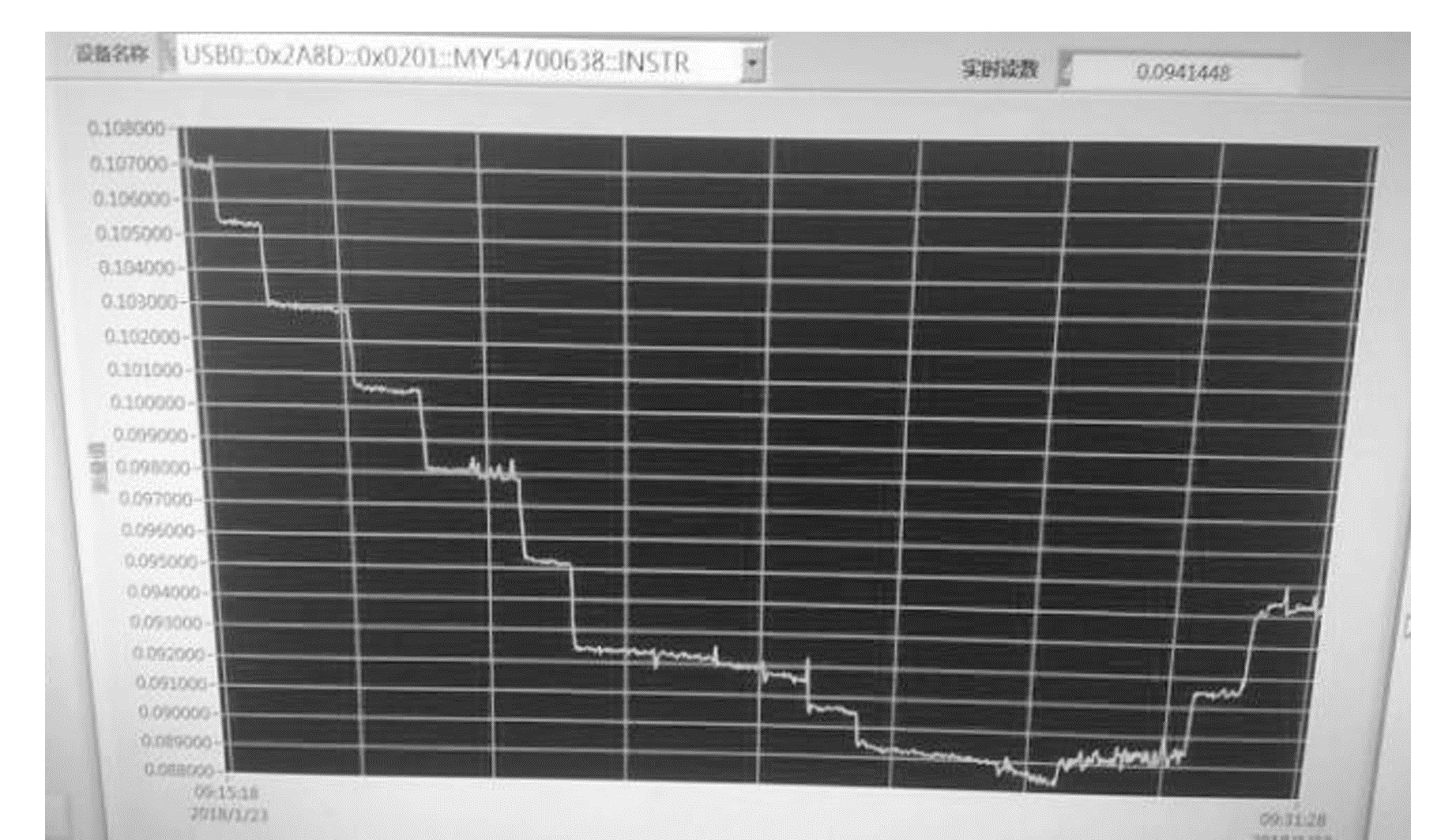
图 4为倾斜实验过程中,用Labview软件采集的超导球位移电压随倾角变化的波形图,图中纵坐标为位移电压,横坐标为时间,采样频率为1 Hz。根据实验和此图像列出位移电压与倾角的关系,结果见表 3。
|
图 4 位移电压随倾角变化 Fig. 4 Displacement voltage changes with the tilt angle |
|
|
表 3 位移电压随倾角变化数据 Tab. 3 Data table of displacement voltage and tilt angle |
图 4中电压波形是调节完X轴方向水平后,Y轴方向的倾角从0.048°开始,每次以0.013°的倾角增加到0.165°的过程,图中电压最低处的倾角为0.139°。位移电压为0时表示超导球处在中心位置,为正值时超导球位于中心位置以下,为负值时超导球位于中心位置以上,电压绝对值越大表示超导球偏离中心位置越远。可以看出,在倾角调节过程中,电压为正,电压值先变小再变大,表示超导球先上升到最高点再下降的变化过程。当磁悬浮系统偏离水平方向倾角最小时,电磁力分力提供的悬浮力最大,超导球能上升到最高处。图 4中电压的峰值处即为倾角最小处,此时倾角为0.139°。从图 4中还可以看出,每调整一次倾角,位移电压变化比较稳定,说明超导球运动比较稳定,且每改变0.013°的倾角,差动电压变化较明显,说明重力测量对倾角的变化很灵敏。图 4中某些台阶出现小毛刺,可能是仪器隔震措施没做好,由外界的随机振动带来的干扰,或者是由调平装置伺服电机的零位漂移带来的干扰。通过此倾斜实验,实现了装置的调平,得到了位移电压随倾角变化的数值关系。
从表 3可看出,当倾角每改变0.013°时,位移电压变化在1.5~3.0 mV,取平均值为2.53 mV,即每改变0.013°倾角引起位移电压变化为2.53 mV。在此超导重力测量装置中,电压与位移关系为±7 V对应1 mm位移,所以2.53 mV电压改变对应1.807×10-7 m的位移变化。根据重力梯度公式,梯度∇=ΔF/ΔS=mΔg/ΔS,重力误差为:
| $ \Delta g = \left( {\Delta S \times \nabla } \right)/m $ | (4) |
式中,ΔS为位移变化,m为超导球质量8 g,仪器梯度为1.0×10-2N/m。在此条件下,可算出1.807×10-7 m位移变化引起的重力改变为22.50 μGal。根据式(3)可计算出0.013°倾角改变引起的重力改变为26.22 μGal,即2.53 mV的位移电压变化对应26.22 μGal的重力变化,与通过式(4)计算得到的22.50μGal的结果非常接近。通过倾斜实验和仪器参数算出的重力精度与理论公式算出的结果非常接近,验证了重力精度与倾角的关系,同时也证明了用此支撑腿调平系统进行倾角测量和调平的有效性和正确性,为超导磁悬浮装置的调平工作和高精度重力测量提供参考。
4 结语通过分析重力测量精度与磁悬浮系统倾角及仪器支撑腿调节高度之间的关系,确定采用交流伺服电机驱动高精度电动缸作为支撑腿进行调平的方案。制作支撑腿调平系统并进行调平实验,倾角调节精度达0.002°,最小位移调节为2.5 μm,由调平引起的最小重力误差约为1 μGal。利用此系统,找到了倾角最小的位置,实现了重力仪调平功能,验证了重力测量精度与倾角间的关系,为超导重力仪的调平工作和高精度重力测量提供参考。
| [1] |
聂仁奇, 章传银, 秘金钟. 超导重力仪观测数据分析[J]. 全球定位系统, 2012, 37(1): 35-38 (Nie Renqi, Zhang Chuanyin, Bei Jinzhong. Analysis of Superconducting Gravimeter Observations[J]. GNSS World of China, 2012, 37(1): 35-38 DOI:10.3969/j.issn.1008-9268.2012.01.010)
(  0) 0) |
| [2] |
吴琼.高精度绝对重力仪关键技术研究[D].北京: 中国地震局地球物理研究所, 2011 (Wu Qiong.The Study of the Key Technology in High-Precision Absolute Gravimeter[D].Beijing: Institute of Geophysics, CEA, 2011)
(  0) 0) |
| [3] |
Sun H P, Xu H Z, Ducarme B, et al. Comprehensive Comparison and Analysis of Tidal Gravity Observations Obtained with Superconducting Gravimeters at Stations in China, Belgium and France[J]. Chinese Science Bulletin, 1999, 44(8): 750-755 DOI:10.1007/BF02909719
(  0) 0) |
| [4] |
Sun H P, Takemoto S, Xu H Z, et al. Precise Tidal Gravity Recorded with Superconducting Gravimeters at Stations Wuhan, China and Kyoto, Japan[J]. Journal of Geodesy, 2001, 74(10): 720-729 DOI:10.1007/s001900000139
(  0) 0) |
| [5] |
陈晓东, 孙和平, 张为民, 等. 用绝对重力仪测定超导重力仪格值的精度分析[J]. 大地测量与地球动力学, 2013, 33(5): 145-149 (Chen Xiaodong, Sun Heping, Zhang Weimin, et al. Accuracy Analysis on Determination of Calibration Factor of a Superconducting Gravimeter Using an Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics, 2013, 33(5): 145-149)
(  0) 0) |
| [6] |
胥靖文, 王晖, 胡新宁, 等. 应用于重力测量的超导磁悬浮系统电磁特性分析[J]. 低温与超导, 2016, 44(4): 1-5 (Xu Jingwen, Wang Hui, Hu Xinning, et al. Analysis of Electromagnetic Properties of Superconducting Suspension System Applied to Gravity Observations[J]. Cryogenics & Superconductivity, 2016, 44(4): 1-5)
(  0) 0) |
| [7] |
孙和平, 徐建桥, 许厚泽. 我国GWR超导重力仪观测资料应用研究进展[J]. 大地测量与地球动力学, 2002, 22(4): 106-111 (Sun Heping, Xu Jianqiao, Xu Houze. Progress in Application Study of Gravity Observations Recorded with a GWR Superconducting Gravimeter in China[J]. Journal of Geodesy and Geodynamics, 2002, 22(4): 106-111)
(  0) 0) |
| [8] |
邢乐林, 李辉, 刘子维, 等. 利用绝对重力测量精密测定超导重力仪的格值因子[J]. 大地测量与地球动力学, 2010, 30(1): 48-50 (Xing Lelin, Li Hui, Liu Ziwei, et al. Scale Factor Calibration of a Superconducting Gravimeter by Using Absolute Gravimetry[J]. Journal of Geodesy and Geodynamics, 2010, 30(1): 48-50)
(  0) 0) |
| [9] |
郑家祺, 宋士元, 吴培钧, 等. 超导重力仪的研制[J]. 低温物理学报, 1988, 10(3): 40-46 (Zheng Jiaqi, Song Shiyuan, Wu Peijun, et al. Study of the Superconducting Gravimeter[J]. Chinese Journal of Low Temperature Physics, 1988, 10(3): 40-46)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39


