传统的地震学理论认为,固体介质中某一点的运动包括平动、转动和变形3种,其中平动是指沿直线往复运动,转动是指沿轴线扭转运动。转动地倾斜是以地面上一条水平直线为转轴的转动。早期地震仪的设计既考虑了平动信号的检测,也考虑了转动地倾斜信号的检测。然而,由于受到当时技术水平的限制,仪器的灵敏度普遍较低,以至于多年来未能记录到可靠的转动地倾斜信号[1],这种状况持续了近70 a(1927~1998年)。在长期缺乏观测证据的情况下,地震引起的转动地倾斜信号是否存在逐渐受到怀疑。20世纪初,传统地震学认为,地震引起的转动不显著甚至可以忽略,这一观点逐渐成为共识。
近年来,随着观测技术的进步,地震观测数据中的通带外信号在观测数据中反复出现,王小龙等[2]利用短周期地震记录资料研究远震接收函数并得到预期的结果。可见,地震记录数据中通带外信号不能简单地作为零点漂移或者干扰来处理,其来源和属性需要进一步研究。事实上,虽然地震计的设计目标主要集中在地面平动的检测上,但几乎所有摆式地震计都不可能区别平动与地倾斜信号,用于检测平动信号的惯性地震计必然对转动地倾斜信号存在响应[3],传统地震观测系统的记录数据中既有平动成分,也有转动地倾斜信号成分[4]。2006年,Pillet等[5]在宽频带海底地震计的通带外数据中发现了占总信号强度90%的地面转动成分。为了从现代地震观测数据中识别地倾斜信号,前人作了大量工作,Kinoshita等[6]在宽频带速度型地震计VSE-355EI的记录数据中观察到Tokachi-Oki M8.3地震时地面倾斜引起的长周期脉冲信号。
2011-03-11日本9.0级大地震之后,云南的地震台站和地倾斜台站同时记录到持续2 d以上的地球自由振荡。由于地震计对倾斜和平动能同时响应,导致记录数据中各种信号相互混叠,难以判断其基本属性。本文通过建立地震计对地倾斜与平动信号的响应模型,利用仿真方法对整个观测过程进行模拟,判断地震计通带外信号与地震波传播过程中等效地面倾斜的关系。
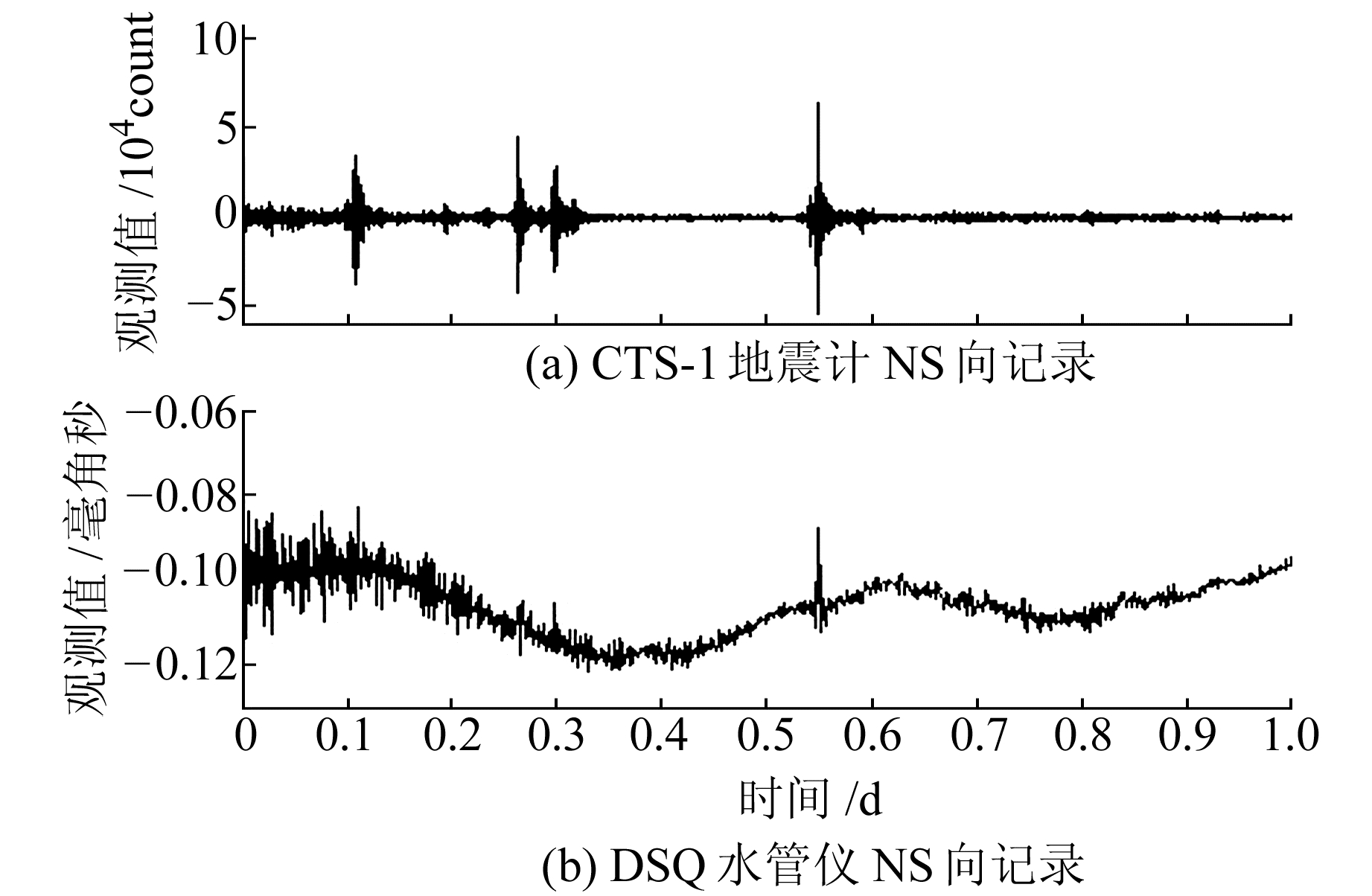
1 观测数据与现象日本M9.0地震发生后,云南省综合观测站(同时安装宽频带地震计与地倾斜观测仪器)记录到了清晰的地球自由振荡,持续时间为2011-03-11~03-13。其中,洱源地震台CTS-1宽频带地震计及DSQ水管地倾斜观测仪记录的地球自由振荡信号如图 1所示。
|
数据时段2011-03-11 21:00:00~03-12 22:59:00 图 1 洱源地震台CTS-1地震计、DSQ水管仪记录数据中的地球自由震荡信号对比 Fig. 1 Earth's free oscillation records of CTS-1 seismometer and DSQ tilter meter at Eryuan station |
图 1中,CTS-1宽频带地震计记录数据的采样率为100 Hz,DSQ水管地倾斜观测仪记录数据的采样率为1/60 Hz。将图 1中的数据在时间坐标中展开,可以看到有一组长周期信号同时出现在地震与地倾斜观测数据之中,如图 2所示。
|
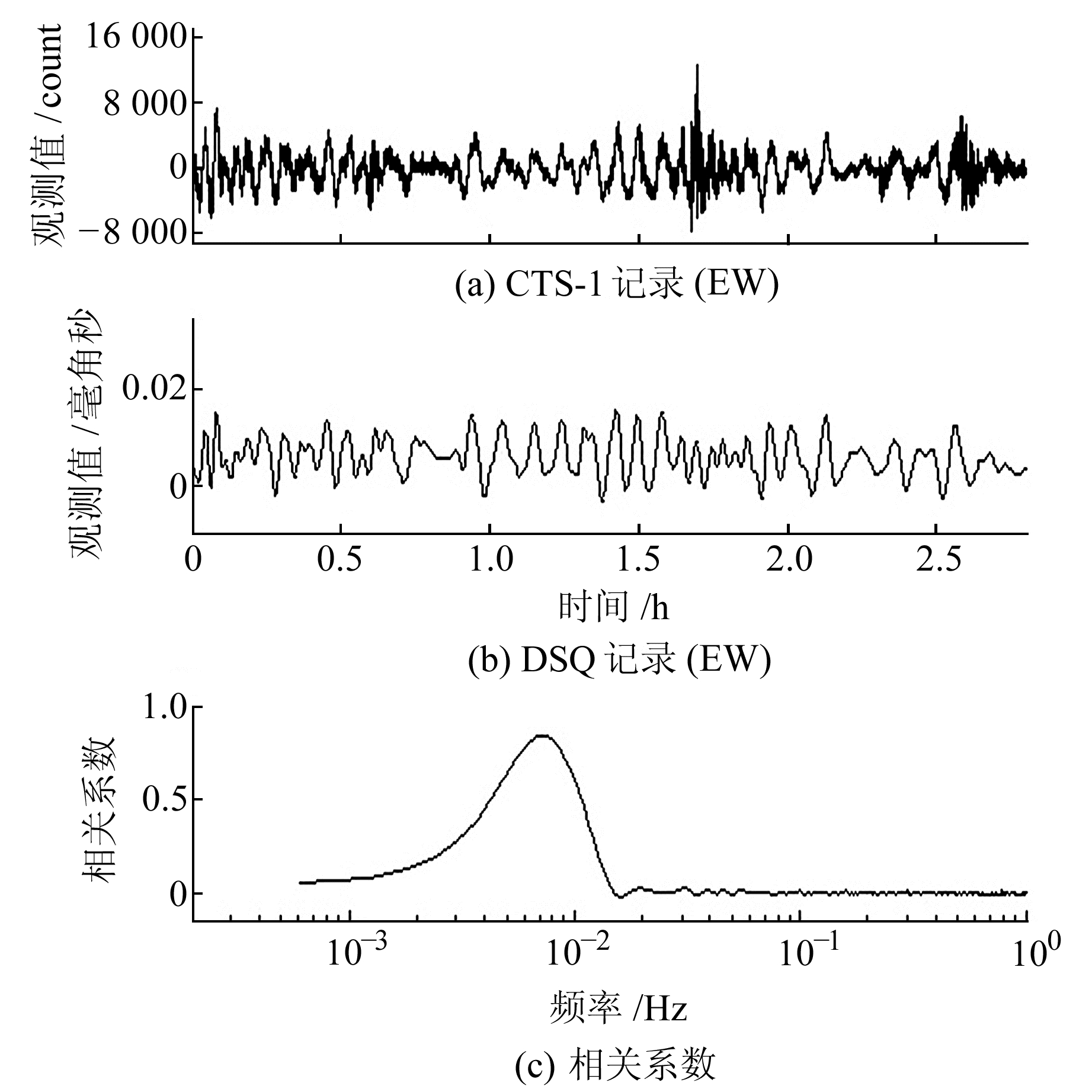
数据时段2011-03-12 00:00:00~03-12 02:24:00 图 2 洱源地震台CTS-1地震计、DSQ水管仪记录数据中的地球自由震荡信号对比s Fig. 2 Earth's free oscillation records of CTS-1 seismometer and DSQ tiltmeter at Eryuan station |
从观测原理上看,图 2(a)中的地震记录信号是地面平动信号,其物理量纲是m/s,而图 2(b)中的信号是地倾斜信号,其物理量纲是rad/s。对比图 2(a)和图 2(b)可以看出,2种记录数据中的低频信号基本相似。由于该低频信号同时出现在地震和地倾斜观测数据中,其物理属性值得进一步研究。
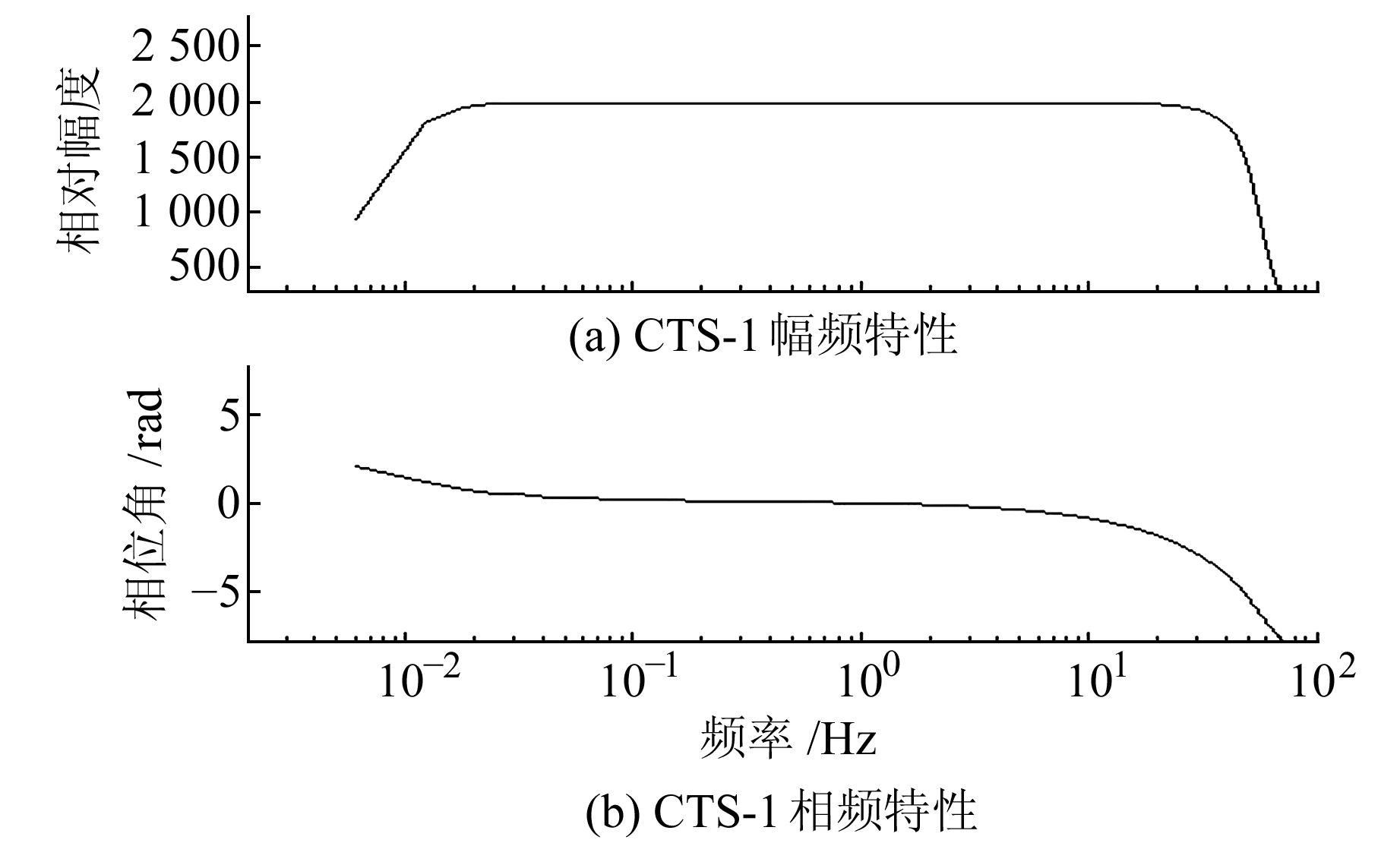
根据CTS-1地震计的结构原理及传递函数[7],得到该地震计对地面平动响应的频率特性,结果见图 3。
|
图 3 CTS-1地震计平动响应频率特性 Fig. 3 Amplitude and phase features of the CTS-1 |
从图 3可以看出,地震计CTS-1对平动信号的响应特性为带通滤波器,其低频截止频率约为120 s。而2011-03-11日本9.0级大地震之后的地面自由振荡信号周期为396 s,频率在CTS-1地震计的通频带之外,如图 3(a)所示,这一现象难以用传统的地震观测理论来解释。
2 模型分析与验算当输入信号为地面平动时,地震计摆体对输入信号响应的运动方程为:
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} + 2\beta {\omega _0}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + \omega _0^2y = - \frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} $ | (1) |
式中,y为摆体运动位移,x为地面运动位移,β为摆体的阻尼系数,ω0为摆体的自振角频率。用正弦信号叠加,合成式(1)中的输入信号
如果既考虑地震计的平动响应,又考虑倾斜响应(忽略较小的二次项),地震计摆体的运动方程为:
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} + 2\beta {\omega _0}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + \omega _0^2y = - \frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} - L\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{t^2}}} - g\theta $ | (2) |
式中,L为摆体的等效倾斜长度,θ为地面倾斜角度,g为重力加速度。对于CTS-1型宽频带地震计,由于开环自振周期T≈6 s,将CTS-1的参数代入计算,可以得出等效的折合摆长。
混合的输入信号为式(2)等号右边的
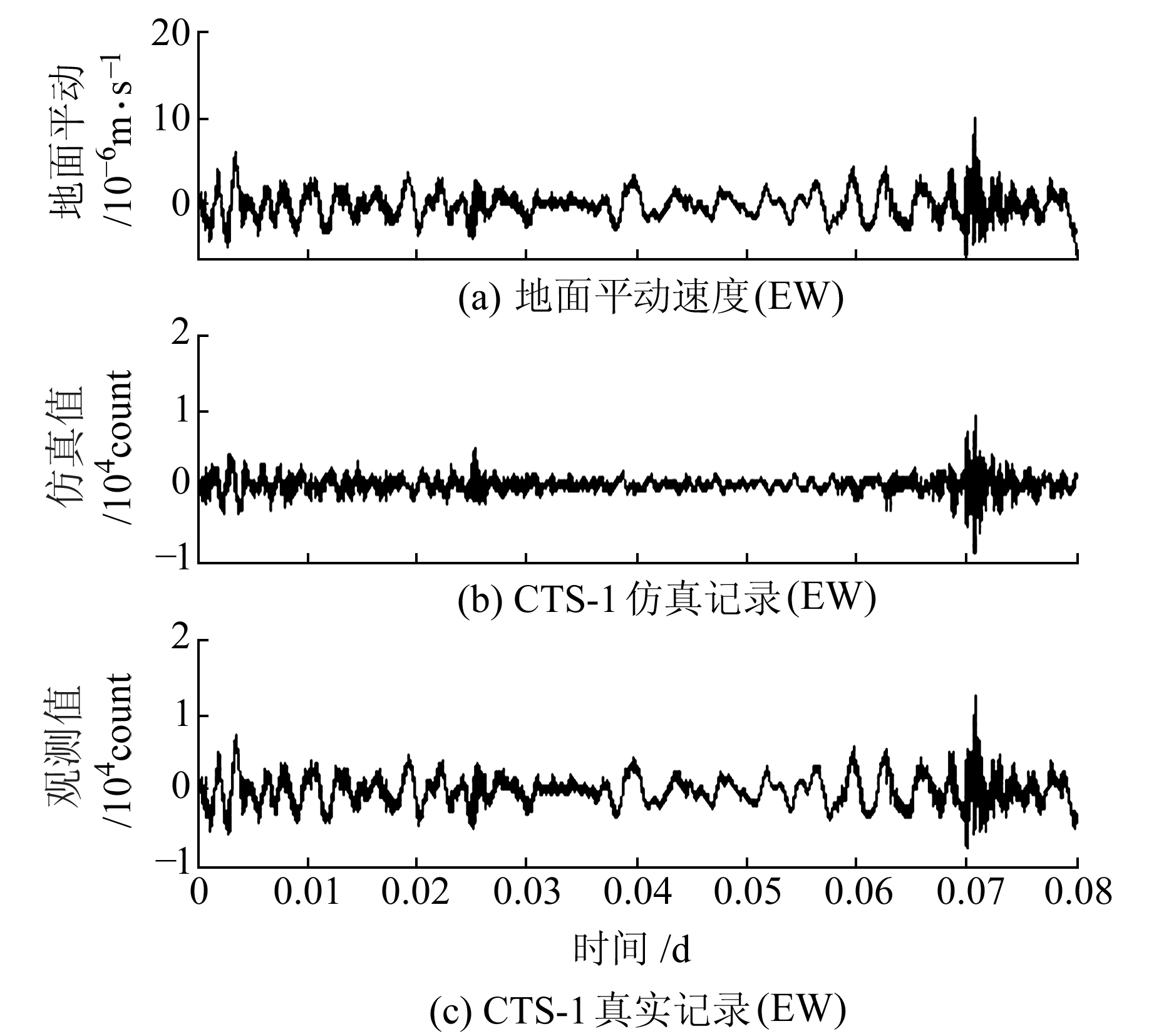
假设图 2(a)的记录信号无论高频或低频都属于平动信号,则该信号代表的地面平动速度见图 4(a)。将该信号作为地震信号输入,计算地震计CTS-1对该信号的响应记录,结果见图 4(b),真实记录如图 4(c)所示。
|
图 4 长周期信号作为平动信号输入时的仿真记录与真实记录对比 Fig. 4 Difference in simulation records and real field records of CTS-1 seismometer when the long period signal is assumed as translation motion |
由图 4可知,如果长周期信号为平动信号,记录数据中的低频信号将会被压制,信号幅度变小并部分丢失(图 4(b)),使记录图像严重偏离真实的地震记录(图 4(c)),故图 2中的长周期信号不属于平动信号。
2.2 基于混合输入假设的数值计算由于惯性地震计必然对倾斜产生响应,且CTS-1记录数据中的低频信号同时出现在地倾斜仪记录数据中(图 2),假定低频信号属于倾斜θ,高频信号属于平动x,上述2个信号按式(2)右端进行叠加得到混合输入信号,该信号对于地震计摆体来说是一个等效的力。
由于地震观测系统是一个线性系统,该系统对多个叠加信号的响应等于对单个信号响应的叠加,因此可以分别计算地震计对平动和倾斜的响应并叠加,得到地震计对混合信号的响应记录。
根据摆体运动方程式(2),摆体位移y对平动速度dy/dt的传递函数为:
| $ H\left( s \right) = \frac{{ - s}}{{\left( {{s^2} + 2\beta {\omega _0}s + \omega _0^2} \right)}} $ | (3) |
摆体位移y对倾斜角度θ的传递函数为:
| $ {F_\theta }\left( s \right) = \frac{{ - {s^2}L - g}}{{\left( {{s^2} + 2\beta {\omega _0}s + \omega _0^2} \right)}} $ | (4) |
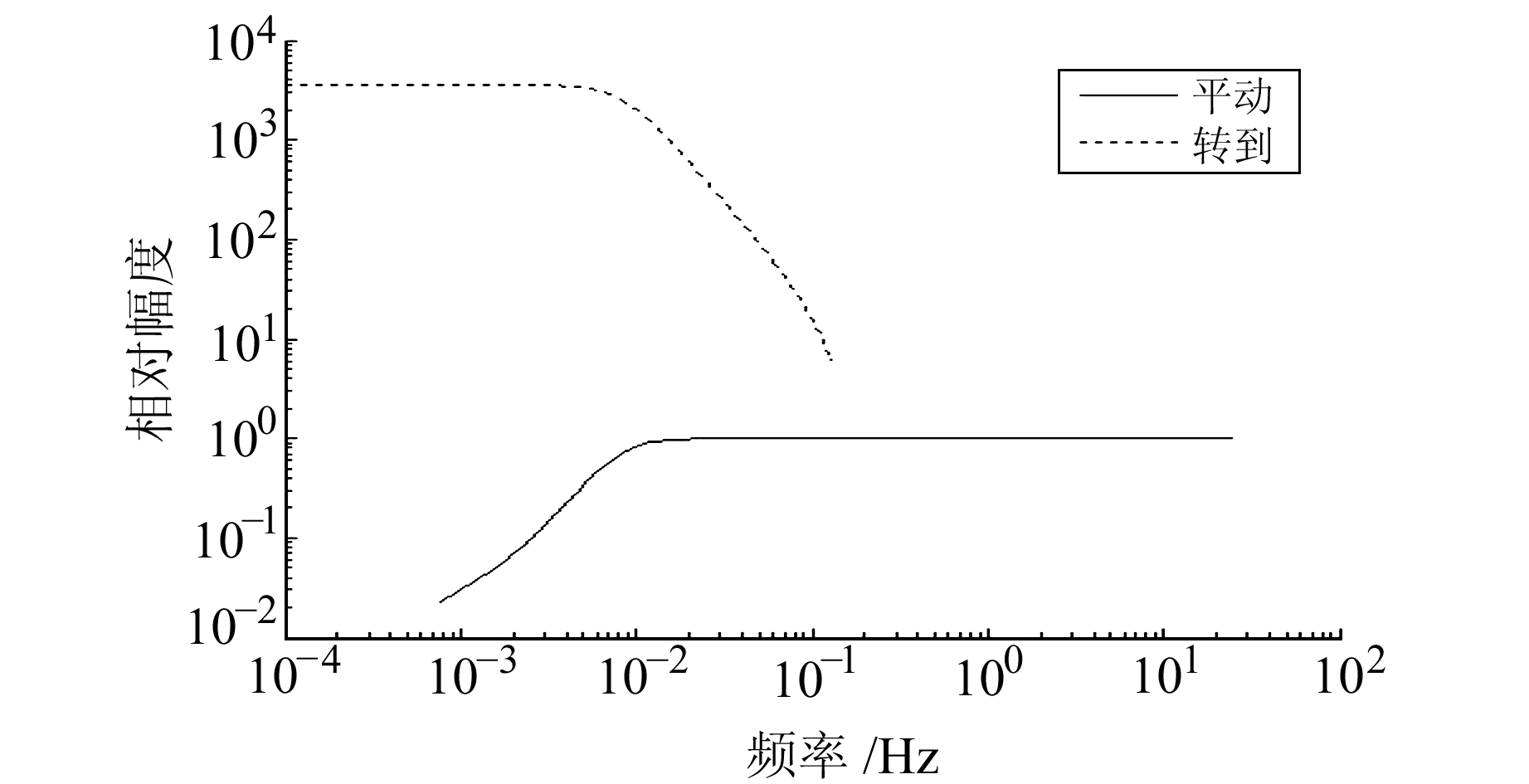
将摆体参数代入式(3)和(4),可以得到摆体对平动速度和倾斜角度响应的幅频特性对比情况,结果如图 5所示。
|
图 5 CTS-1地震计摆体对平动和倾斜信号响应的理论特性对比 Fig. 5 Difference in response performance of CTS-1 seismometer to translation signal and tilt motion |
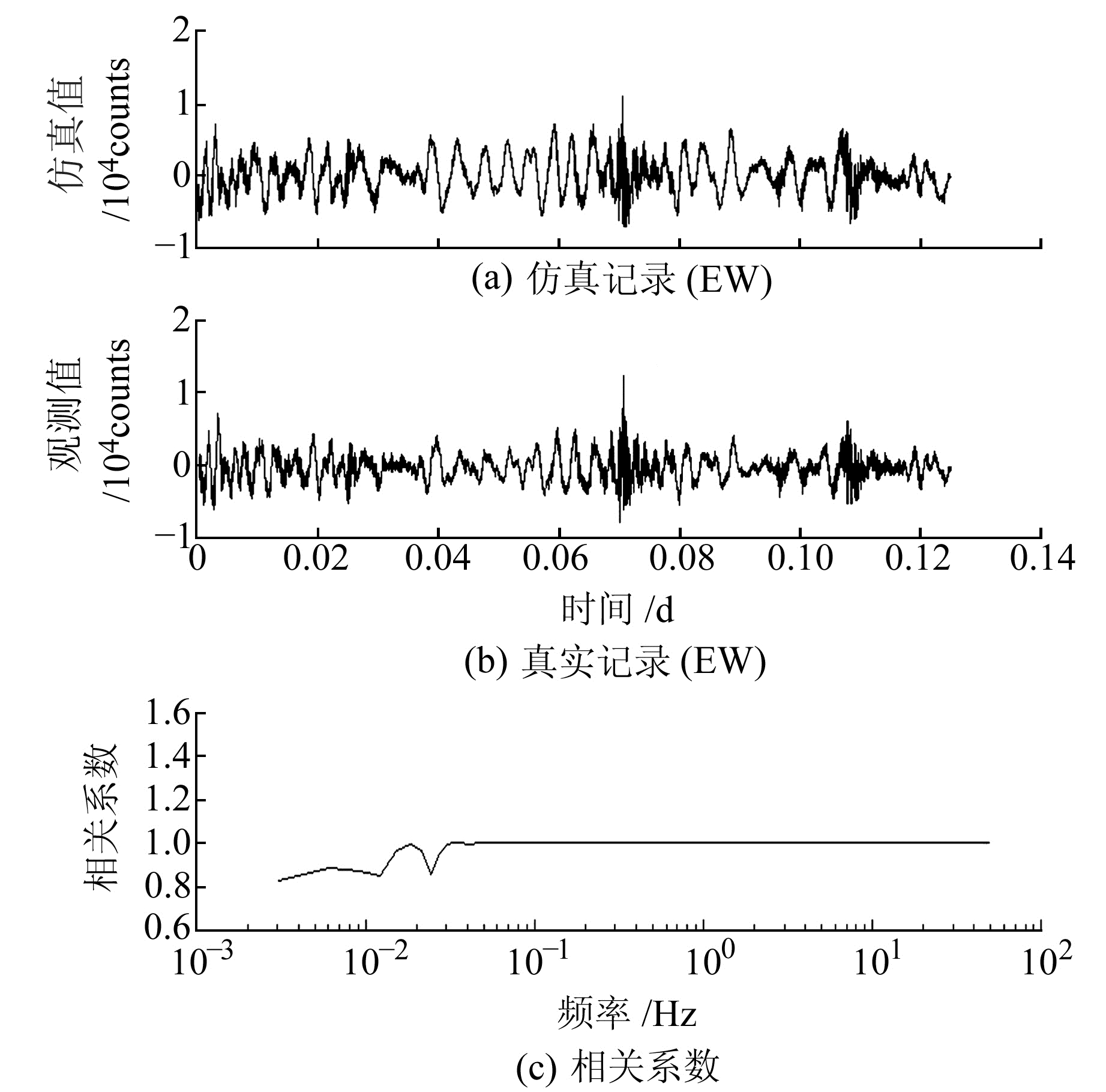
用地倾斜记录数据作为倾斜信号θ,从测震记录中提取通带内的信号作为平动信号x,将高频速度信号代入式(3),长周期倾斜信号代入式(4),分别得到地震计对2种信号的响应。将2种响应记录叠加,即可得到地震计对混合输入信号的仿真记录,该记录波形(图 6(a))与真实记录波形(图 6(b))基本相同,两者的相关系数见图 6(c)。
|
图 6 长周期信号作为倾斜信号输入时CTS-1的仿真记录与真实记录对比 Fig. 6 Simulation records and real field records of CTS-1 seismometer when the long period signal is assumed as tilt motion |
由图 6可知,如果长周期信号为倾斜信号,仿真结果与真实记录差别较小,如图 6(a)和6(b)所示。分析仿真结果与真实记录之间的相关性,结果表明,2组数据之间的相关系数在地震计通频带内接近于1。可见,CTS-1记录数据中的长周期信号属于等效倾斜信号的假设是成立的。
3 结语尽管地震引起的地面倾斜信号不可能以波的形式传播是地球物理学的基本结论,但地震波(特别是长周期面波和地球自由振荡)在传播过程中对地震计的机理存在着倾斜效应。常规地震计不仅对平动信号有响应,而且对地倾斜信号及地震波传播过程中引起的倾斜效应有响应,2种响应在记录数据中相互叠加难以分离。基于地震计对平动与倾斜响应的数学模型,利用地震与地倾斜同点观测记录的数据,可以初步判断地震记录中某一频段信号的属性。结果表明,在地震观测实践中,记录数据中的通带外信号可能来源于地震波传播过程中引起的等效倾斜,也可能来源于地震计幅频特性对通带外信号的不完全截取,还可能两者兼而有之。因此,不能简单地将通带外信号作为不可靠信号丢弃,信号的具体属性需要根据实际情况作进一步分析。
| [1] |
Lee W H K, Celebi M, Todorovska M I, et al. Introduction to the Special Issue on Rotational Seismology and Engineering Applications[J]. Bulletin of the Seismological Society of America, 2009, 99(2B): 945-957 DOI:10.1785/0120080344
(  0) 0) |
| [2] |
王小龙, 倪四道, 刘渊源, 等. 利用远震接收函数分析三峡库区重庆段地壳厚度变化[J]. 地震地质, 2010, 32(4): 543-551 (Wang Xiaolong, Ni Sidao, Liu Yuanyuan, et al. Study of Crustal Thickness Variation in Chongqing Section of Three Gorges Reservoir Area from Teleseismic Receiver Function Method[J]. Seismology and Geology, 2010, 32(4): 543-551 DOI:10.3969/j.issn.0253-4967.2010.04.002)
(  0) 0) |
| [3] |
Bradner H, Reichle M. Some Methods for Determining Acceleration and Tilt by Use of Pendulums and Accelerometers[J]. Bulletin of the Seismological Society of America, 1973, 63(1): 1-7
(  0) 0) |
| [4] |
Pillet R, Virieux J. The Effect of Seismic Rotations on Inertial Sensors[J]. Geophysical Journal International, 2007, 171(3): 1314-1323 DOI:10.1111/j.1365-246X.2007.03617.x
(  0) 0) |
| [5] |
Pillet R, Deschamps A, Legrand D, et al. Interpretation of Broadband Ocean-Bottom Seismomenter Horizontal Data Seismic Background Noise[J]. Bulletin of the Seismological Society of America, 2009, 99(2B): 1333-1342 DOI:10.1785/0120080123
(  0) 0) |
| [6] |
Kinoshita S, Ishikawa H, Satohy T. Tilt Motion Recorded at Two WISE Sites for the 2003 Tokachi-Oki Earthquake(M8.3)[J]. Bulletin of the Seismological Society of America, 2009, 99(2B): 1251-1260 DOI:10.1785/0120080090
(  0) 0) |
| [7] |
蔡亚先, 吕永清, 周云耀, 等. CTS-1甚宽频带地震计[J]. 大地测量与地球动力学, 2004, 24(3): 109-114 (Cai Yaxian, Lü Yongqing, Zhou Yunyao, et al. CTS-1 Very Broadband Seismometer[J]. Journal of Geodesy and Geodynamics, 2004, 24(3): 109-114)
(  0) 0) |
| [8] |
崔庆谷, 华均, 杨星. 强震、微震记录数据差异的模型验算[J]. 地震学报, 2012, 34(5): 667-675 (Cui Qinggu, Hua Jun, Yang Xing. Checking the Distinction between Accelerator and Seismometer Records by Means of Mathematical Model[J]. Acta Seismologica Sinica, 2012, 34(5): 667-675 DOI:10.3969/j.issn.0253-3782.2012.05.008)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


