2. 浙江省河海测绘院,杭州市复兴南街268号, 310008
激光扫描技术的进步使得三维激光扫描仪在工业扫描、文物测绘等领域得到了广泛应用[1]。在点云数据处理过程中,配准对后续处理影响重大,最经典的算法就是20世纪90年代初计算机视觉研究者Bes等[2]提出的迭代最近点(iterative closet point,ICP)算法,通过迭代选择对应点的计算,满足对应点之间的距离误差最小条件即可得出旋转平移变换矩阵[3-4]。近年来,许多学者针对搜索最近点过程和加快收敛速度方面进行改进,提高了ICP算法的精度和效率。Natasha等[5]分析了ICP算法中的配准质量问题;Chen等[6]及Bergevin等[7]提出point-to-plane搜索最近点的精确配准方法;Park等[8]提出contractive-projection-point搜索最近点的配准方法;Mitra等[9]和Ko等[10]进行深入研究,提出不同的配准算法。
但ICP算法以最小二乘为解算原则,存在粗差点时算法抗差性弱,以空间欧氏距离最小为原则确立对应点对不具客观性。因此,本文提出一种改进的基于点云权重的ICP算法,并通过具体实例验证其有效性。
1 标准ICP算法概述ICP算法是点集到点集的配准算法,其基本思想是将给定的目标点集P通过一系列旋转和平移变换,最终变换到参考点集Q中,实现数据的融合。其基本前提为假设P是Q的子集,具体过程为:1)对于目标点集P中的每个点,在参考点集Q中寻找与其空间欧氏距离最近的一个点组成最近点对集合;2)以旋转平移后点对残差平方和最小为目标,在最小二乘原则下求解出一个最优的变换M;3)迭代地进行这个过程,直到满足某种精度要求为止。其变换关系式和收敛准则为:
| $ \mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{RP}} + \mathit{\boldsymbol{T}} $ | (1) |
| $ d = \sum\limits_{i = 1}^n {{{\left\| {{q_i} - \mathit{\boldsymbol{R}} \cdot {p_i} - \mathit{\boldsymbol{T}}} \right\|}^2}} $ | (2) |
式中,P和Q分别为目标点集和参考点集,R为旋转矩阵,T为平移向量,d为目标函数。
ICP算法是以残差平方和最小为解算准则来求解变换参数的,当配准残差服从正态分布时,最小二乘具有最优统计性质,算法能计算出最佳结果。但最小二乘估计不具备抗差性,如果残差中包含了粗差影响,数据就会偏离正态分布,此时用最小二乘估计得出的结果将会出现偏差。而且,扫描仪在扫描时是对物体表面进行随机性扫描,ICP算法以空间欧氏距离最小为原则确立对应点对不具客观性,没有考虑到点云数据自身的内部差异,没有对点对在配准计算中的权重作出区分。
2 点云配准算法改进现有的针对ICP配准点云定权的方法都是简单地利用点对的距离绝对值的倒数作为权重值,这种方法形象直观,并且在某些情况下能起到抵御粗差的作用。但由于没有充分利用点对残差的统计分布规律,简单残差倒数的定权法不具备通用性。当ICP配准残差服从正态分布规律时,可以将残差对应的正态分布曲线函数作为残差的定权函数,即
| $ P\left( v \right) = f\left( v \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }} \cdot {{\rm{e}}^{\frac{{ - {v^2}}}{{2{\sigma ^2}}}}} $ | (3) |
式(3)满足残差绝对值大的权重小、残差绝对值小的权重大的定权原则,而且能够保证权重值在0~1之间。
设(pi, qi)为ICP配准某次迭代计算的对应点对,经过变换后的残差为vi=(vxi, vyi, vzi),由式(3)可以计算出3个方向残差分量的权重值为:
| $ \left\{ \begin{array}{l} {P_{xi}} = P\left( {{v_{xi}}} \right) = {\rm{e}}\frac{{ - v_{xi}^2}}{{2\sigma _x^2}}\\ {P_{yi}} = P\left( {{v_{yi}}} \right) = {\rm{e}}\frac{{ - v_{yi}^2}}{{2\sigma _y^2}}\\ {P_{zi}} = P\left( {{v_{zi}}} \right) = {\rm{e}}\frac{{ - v_{zi}^2}}{{2\sigma _z^2}} \end{array} \right. $ | (4) |
式中,σx2、σy2、σz2分别为3个方向残差的方差,由残差值可近似地计算出:
| $ \left\{ \begin{array}{l} \sigma _x^2 = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{v_{xi}} - \overline {{v_x}} } \right)}^2}} \\ \sigma _y^2 = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{v_{yi}} - \overline {{v_y}} } \right)}^2}} \\ \sigma _z^2 = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{v_{zi}} - \overline {{v_z}} } \right)}^2}} \end{array} \right. $ | (5) |
式中,vx、vy、vz分别为3个方向残差的均值,n为残差的个数。顾及
| $ \begin{array}{*{20}{c}} {{P_i} = }\\ {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\left( {{\sigma _x} \cdot {\rm{e}}\frac{{ - v_{xi}^2}}{{\sigma _x^2}} + {\sigma _y} \cdot {\rm{e}}\frac{{ - v_{yi}^2}}{{\sigma _y^2}} + {\sigma _z} \cdot {\rm{e}}\frac{{ - v_{zi}^2}}{{\sigma _z^2}}} \right)} \end{array} $ | (6) |
式(6)即为基于配准残差分布函数的点对权重计算公式。
标准ICP算法将每个点对都看成是权重为1的计算值,即各个点对对最终计算结果的影响是相同的。基于点云权重改进的ICP算法的核心,是对每个点对根据其配准计算的残差值利用公式(6)计算出其对应的权重值,在此基础上解求变换参数。
由于选权迭代法和ICP算法本身都是一个迭代的过程,本文基于点云权重改进的ICP算法利用了M估计中选权迭代法的思想,包含了常规ICP迭代和选权迭代,是一个复合迭代的过程。因此,在传统ICP算法的每步迭代计算中还包含了一组选权迭代计算,每次选权迭代计算都是针对同一组对应点对来进行的。根据该组点对的残差进行定权,然后在附加点对权重的基础上不断重新计算旋转平移参数,在这一过程中每次都会计算出新的残差,相应点对的权重也会不断调整,直到满足某种条件为止。在一组选权迭代计算完成一次ICP迭代计算后,运用该次计算得出的变换参数重新搜索最近点以进行下一次ICP迭代计算,根据2次ICP迭代计算的残差平方和之差的大小来判断迭代计算是否完成。算法详细过程如下:
1) 给定2个已经经过初始配准的待配准点集P和Q;
2) 对点集P中的每一个点,在Q中寻找与其对应的最近点,在最小二乘准则下计算初始旋转参数R、初始平移参数t、初始残差V(Vx, Vy, Vz),使得
3) 根据残差V,利用定权公式(6)给每个点对i赋权重值Pi;
4) 在附加点对权重的基础上重新计算新的旋转参数R,平移参数t及点对残差V,使
5) 重复3)~4),直到相邻2次选权迭代计算出来的点对残差值Vk及Vk+1充分接近,即满足|Vk-Vk+1| < τ时停止;
6) 重复2)~5),当相邻2次ICP配准的残差平方和ek和ek+1满足|ek+1-ek|≤σ时停止;
7) 最后一次迭代计算得出的旋转平移参数即为所求。
3 算法实验 3.1 常规粗差点实验分析由于常规粗差点产生的原因很多,其规律很难把握,因此不易在实际的点云数据中提前对其准确定位。为验证本文算法对常规粗差点的影响,在实验中采取人为增加粗差点的方法,确保残差呈正态分布。向经过公共点提取后的雕像数据的左视点云中加入300个粗差点,这些粗差点加入在雕像基座的正前方,以确保粗差点都在配准的公共区域内部(图 1),图 1(b)矩形方框内即为加入粗差点的区域。

|
图 1 公共点云示意图 Fig. 1 The schematic of public cloud point |
对以上点云数据分别采用标准ICP算法和本文算法进行配准,并将最终求解出来的配准结果作用于全部数据集,得到的配准结果按左、中、右3个视角方向对比显示(图 2和3)。

|
图 2 传统ICP算法示意图 Fig. 2 The schematic of traditional ICP algorithm |

|
图 3 本文算法示意图 Fig. 3 The schematic of this article algorithm |
从图 2可以看出,传统ICP算法的配准结果在雕像基座边缘处存在明显的错开现象,而雕像基座上部的人物部位拼接吻合度良好,说明粗差点对传统ICP算法的解算产生了干扰,主要影响区域为存在粗差的雕像基座部位。经过本文算法得出的配准结果(图 3)从3个视角来看,左、右雕像点云都很好地拼接到了一起,基座部位没有出现明显的错位现象,说明本文算法有效地抵御了粗差点对配准结果的干扰。将2种算法每次迭代时的均方误差进行统计,结果见图 4和表 1。

|
图 4 2种算法迭代残差统计 Fig. 4 The residual chart of two algorithms iterative |
|
|
表 1 2种算法计算性能比较 Tab. 1 The performance comparison of two algorithms compute |
从图 4可以看出,本文算法迭代计算的收敛速度总体上要快于传统算法。由表 1可知,本文算法计算耗时多于传统ICP算法,这是因为本文算法在每一步常规ICP迭代计算中都要进行一组选权迭代计算,增加了算法的时间和空间,但得出的均方根误差要小于传统算法,计算精度更高。
3.2 边缘粗差点实验分析边缘粗差点是不具有对应关系的非公共点,是影响ICP算法精度的另一重要因素,现采用存在边缘粗差点的一组数据分别进行计算分析。实验数据为采用Trimble GXTM型三维激光扫描仪对某学校三峡石按左右视角扫描获得的两站点云数据(图 5),分别运用本文改进的ICP算法及传统ICP算法进行最终配准,结果见图 6。

|
图 5 扫描点云 Fig. 5 Scanning point cloud |

|
图 6 配准效果图 Fig. 6 Registration renderings |
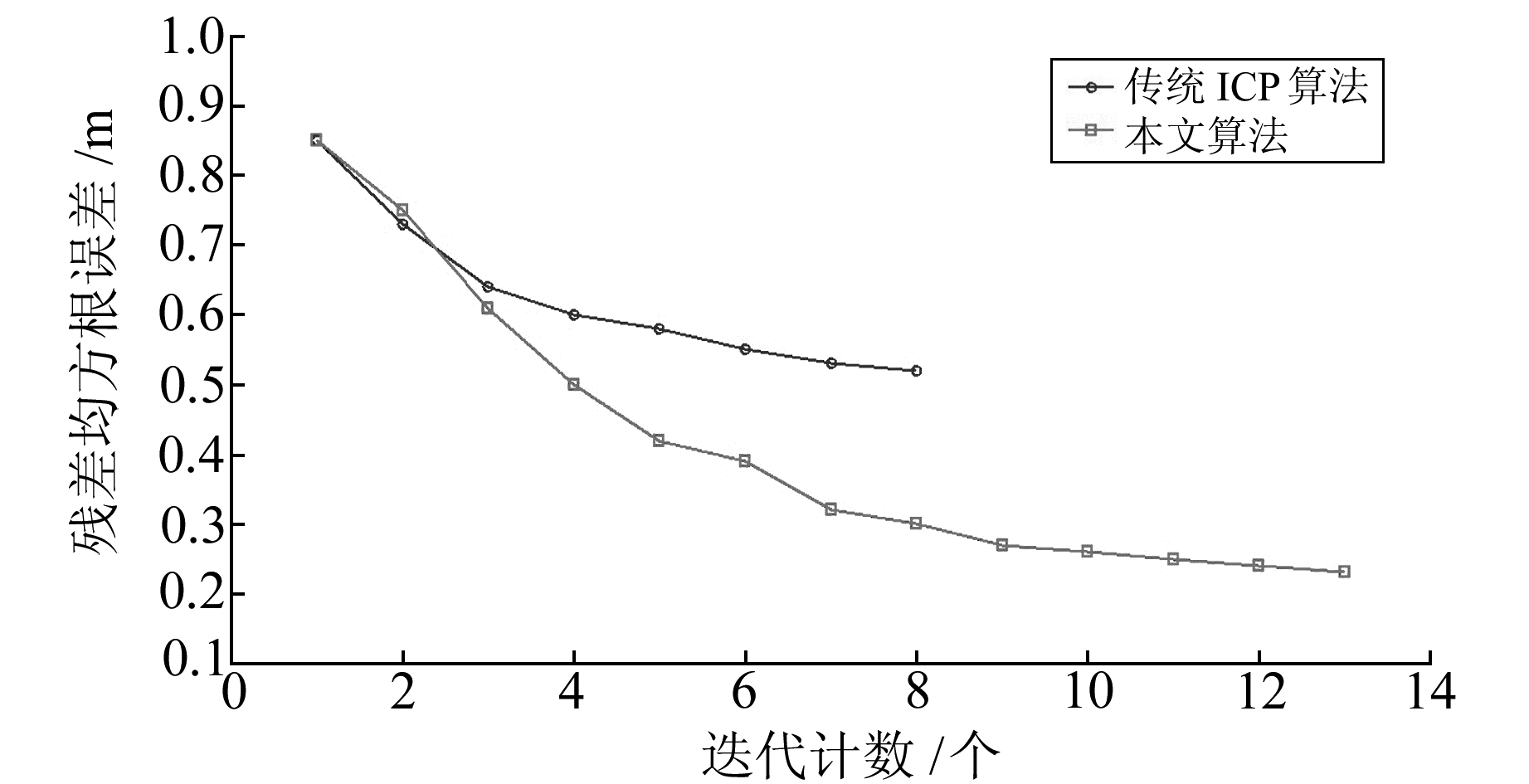
从图 6可以看出,当有边缘点存在时,传统ICP配准算法配准结果出现明显的错位现象,无法满足后续操作的要求,而本文改进算法的配准结果良好。将2种算法迭代计算的均方根误差作为衡量精度的指标进行统计,结果见图 7,其计算性能比较见表 2。
|
图 7 2种算法迭代残差统计 Fig. 7 The residual chart of two algorithms iterative |
|
|
表 2 2种算法计算性能比较 Tab. 2 The performance comparison of two algorithms compute |
由图 7和表 2可知,传统ICP算法配准结果较差。本文基于点云权重改进的ICP算法从最终配准效果和计算进度来看都较传统ICP算法要好,原因在于由边缘粗差点构建的最近点对参与配准后的残差值一般都会很大,而由公共点对计算出的残差值要小很多。在选权迭代计算时,残差大的点对不断被赋以较小的权值,残差小的点对不断被赋以较大的权值,经过多次选权迭代计算,边缘粗差点对对配准计算结果的影响将会变得很小,配准结果主要是由具有对应关系的公共点对所确立。
4 结语针对配准数据中的常规粗差点和边缘粗差点问题,本文在传统ICP算法的基础上对点云权重进行改进,并与传统ICP算法进行比较分析。可以看出,本文基于点对权重改进的ICP算法能够有效处理配准数据中存在粗差的情况,是一种比较精确的抗差配准算法,但仍存在计算耗时大等缺点,在精度和效率两方面没有做到兼顾,具有改进空间。
| [1] |
郑莉.基于结构光的不规则钣金件三维量测[D].武汉: 武汉大学, 2007 (Zheng Li. 3D Measurement of Irregular Sheetmetal Parts Based on Structured Light[D]. Wuhan: Wuhan University, 2007)
(  0) 0) |
| [2] |
Besl P J, Mckay N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256 DOI:10.1109/34.121791
(  0) 0) |
| [3] |
Natasha G, Leslie I, Rzymon R, et al. Geometrically a Table Sampling for the ICP Algorithm[C]. International Conference on 3D Digital Imaging and Modeling, Banff, 2003
(  0) 0) |
| [4] |
郑德华, 岳东杰, 岳建平. 基于几何特征约束的建筑物点云配准方法[J]. 测绘学报, 2008, 37(37): 465-468 (Zheng Dehua, Yue Dongjie, Yue Jianping. Geometric Feature Constraint Based Algorithm for Building Scanning Point Cloud Registration[J]. Acta Geodaetica et Cartographic Sinica, 2008, 37(4): 465-468)
(  0) 0) |
| [5] |
Gelfand N, Ikemoto L, Rusinkiewicz S, et al. Geometrically Sampling for the ICP Algorithm[EB/OL]. http:www.cs.princeton.edu/gfx/bubs/Genlfand2003GSS/stabicp.pdf, 2004-05-18
(  0) 0) |
| [6] |
Chen Y, Medioni G. Object Modeling by Registration of Multiple Range Images[J]. Image and Vision Computing, 1992, 10(3): 145-155 DOI:10.1016/0262-8856(92)90066-C
(  0) 0) |
| [7] |
Bergevin R, Soucy M, Gagnon H, et al. Toward a General Multi-View Registration Technique[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(5): 540-547 DOI:10.1109/34.494643
(  0) 0) |
| [8] |
Park S Y, Subbarao M. An Accurate and Fast Point-to-Plane Registration Technique[J]. Pattern Recognition Letters, 2003, 24(16): 2967-2976 DOI:10.1016/S0167-8655(03)00157-0
(  0) 0) |
| [9] |
Mitra N J, Gelfand N, Pottmann H, et al. Registration ofPoint Cloud Data from a Geometric Optimization Perspective [C].The 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Nice, 2004
(  0) 0) |
| [10] |
Ko K H, Maekawa T, Patrikalakis N M. An Algorithm for Optimal Free-form Object Matching[J]. Computer-Aided Disgin, 2003, 35(10): 913-923 DOI:10.1016/S0010-4485(02)00205-1
(  0) 0) |
2. Zhejiang Surveying Institute of Estuary and Coast, 268 South-Fuxing Street, Hangzhou 310008, China
 2019, Vol. 39
2019, Vol. 39

