2. 中国科学院大学, 北京市玉泉路19号甲, 100049
对流层延迟误差是全球导航卫星系统(GNSS)等空间大地测量技术的主要误差源之一,包括干延迟(ZHD)和湿延迟(ZWD)2个部分。其中,干延迟占比约为90%,可以通过模型较精确地获得;湿延迟占比只有10%,难以通过模型准确计算[1]。在标准大气状况下,天顶方向对流层延迟(ZTD)可达2.3 m左右,在低高度角时,ZTD可达20 m以上,因此必须对ZTD进行正确的估计。目前,常用的对流层估计方法主要有模型改正法、参数估计法、差分法及外部修正法[2],在实际GNSS定位导航应用中,用模型改正法较为方便[3]。
为满足实时定位与导航需要,国内外学者根据气象资料提出一系列全球对流层天顶延迟改正模型,包括UNB3模型[4]、EGNOS模型[5]、GPT2w模型[6]、TropGrid2模型[7]、IGGtrop模型[8]、GZTD模型[9]等。其中,UNB3模型和EGNOS模型为条带模型,其余均为格网模型。2017年,Zhang等[10]基于中国区域的GNSS观测资料构建了格网对流层产品——GTPs模型,可向用户提供实时ZTD改正服务。格网对流层模型不仅顾及对流层天顶延迟的纬向变化,同时也考虑其在经向上的差异[8]。与条带模型相比,格网对流层模型有一定优势,也是目前对流层研究的热点。
格网对流层模型在全球范围的精度已有较多讨论,但针对中国区域的分析较少。Zhang等[3]使用中国地壳运动观测网络(CMONOC)中几十个站点的观测数据对IGGtrop模型进行评估,平均偏差(bias)和均方根误差(RMS)分别为-0.3 cm和4.4 cm;Zhou等[11]使用中国区域的探空数据对GPT2w模型进行精度评估,平均bias和RMS分别为-1.3 cm和4.4 cm;Zhang等[10]对GTPs模型进行精度评估,平均bias和RMS分别为0.1 cm和1.8 cm。
虽然这些格网对流层模型在中国区域都已经评估过精度,但由于这些数据并不同源,未将模型进行统一评估,无法比较各种格网模型的优劣,而且这些评估都是基于地面站,未对飞行器定位导航中ZTD模型的精度进行分析。随着中国北斗导航卫星系统(BDS)的不断发展,中国的BDS用户显著增多,如何选择中国区域内精度相对较高的格网对流层模型是目前亟待解决的问题。采用探空气球数据和GNSS数据均可评估模型,考虑到GTPs模型构建时占用了中国区域大部分的GNSS站,本文将中国区域探空数据计算的ZTD作为真值,来评估GPT2w模型、IGGtrop模型和GPTs模型的精度。
1 对流层延迟基本原理和常用格网模型介绍 1.1 对流层延迟基本原理对流层延迟误差通常是指卫星信号通过50 km以下未被电离的中性大气层时产生的信号延迟。对流层延迟ZTD可由式(1)求出:
| $ {\rm{ZTD}} = {10^{ - 6}}\int_{{h_0}}^\infty {N{\rm{d}}h} $ | (1) |
式中,N为大气折射指数,h0为测站高度,h为高度。
大气折射指数与传播路径的气温、气压和水汽压等气象元素有关。精确的大气折射指数计算公式为:
| $ N = \frac{{{k_1}\left( {P - e} \right)}}{T} + \frac{{{k_2}e}}{T} + \frac{{{k_3}e}}{{{T^2}}} $ | (2) |
式中,k1、k2和k3为折射系数,分别为77.689 K/hPa、71.295 2 K/hPa和3 775 463 K2/hPa;P和e分别为大气压和水汽压,单位为hPa;T为温度,单位为K。
1.2 对流层延迟格网模型介绍一般情况下,测站信号传播路径的气象参数很难获取,只能通过测站上的气象数据建立数学模型,近似地求出ZTD改正,或者在GNSS数据处理中将ZTD作为参数求解。本文主要介绍国际上公认的精度较高的GPT2w模型、IGGtrop模型及GTPs模型。
1.2.1 GPT2w模型Böhm等[6]根据欧洲中期天气预报中心(ECMWF)2001~2010年的ERA-37数据建立全球对流层天顶延迟模型(GPT2w)。该模型将全球划分为1°×1°和5°×5°两种格网,并提供格网点的气象参数表,分别记为GPT2_1w和GPT2_5w,并假定格点上的气象参数随时间仅包含1 a周期变化和0.5 a周期变化,垂直方向上的温度随高度呈线性变化,气压随高度呈指数变化。用户根据测站点的大地坐标和儒略日,可计算出测站所在格网点的气象参数,然后插值计算出测站的气象参数,最后计算ZTD。
1.2.2 IGGtrop模型Li等[8]根据美国国家环境预报中心(NCEP)提供的2006~2009年大气资料, 构建了适用于中国BDS的全球对流层天顶延迟模型(IGGtrop)。该模型将全球划分为2.5°×2.5°×1 km的三维网格,最高高度为25 km,并提供各格网点的ZTD参数表。在赤道地区,该模型考虑了ZTD的1 a周期变化和0.5 a周期变化,其他地区仅考虑1 a周期变化。用户根据测站大地坐标和年积日,可计算出测站所在三维格网点的ZTD,然后插值计算出测站的ZTD。
1.2.3 GTPs模型Zhang等[10]基于CMONOC中210个GNSS测站数据,建立了覆盖中国区域的GTPs模型。该模型将中国划分为2.5°×2°的格网,通过插值和高程改正,将GNSS站的ZTD归算到格网点上。通过分析中心,将时间分辨率为30 s的GPTs模型实时播发给授权用户,用户可根据测站坐标选择测站附近120 km、高差1.5 km内的格点数据,插值计算出测站的ZTD。
2 数据和方法美国国家气象数据中心(NCDC)提供的全球站点无线电探空资料数据集(IGRA),是目前全球范围内时空密度最高、资料最完整的高质量探空资料数据集。该数据集包含中国区域100多个探空站逐日(每天00:00和12:00)探空资料。探空气球将无线电探空仪携带到高空,可以测量从地面到约30 km高度范围内Hi(i=1, 2, …, n)高度处的温度、气压、相对湿度等气象要素。根据这些气象数据,就可以计算出天顶对流层延迟ZTDRS。
当探空仪最高高度过低时,计算得到的ZTDRS偏差比较大,因此在计算之前,通常需要剔除最高高度低于24 km且气压大于30 hPa的观测数据。经过预处理后的探空气象数据解算的ZTDRS精度可达到5 mm,因而常被作为其他模型的参考值[1]。
ZTDRS计算方法为:将气象参数P、T、e代入式(2),计算各高度层上的大气折射指数Ni(i=1, 2, …, n),然后对Ni进行积分得到ZTD:
| $ \begin{array}{*{20}{c}} {{\rm{ZTD}} = \frac{1}{2} \times {{10}^{ - 6}}\sum\limits_i^{n - 1} {\left[ {\left( {{H_{i + 1}} - {H_i}} \right)\left( {{N_{i + 1}} + } \right.} \right.} }\\ {\left. {\left. {{N_i}} \right)} \right] + \Delta {\rm{ZTD}}} \end{array} $ | (3) |
式中,ΔZTD为超出探空气球最高高度部分的对流层延迟残差,可以由Saastamoinen模型估算:
| $ \Delta {\rm{ZTD}} = \frac{{0.002\;277P\left( {{H_{\max }}} \right)}}{{1 - 0.002\;66 \times \cos 2\varphi - 2.8 \times {{10}^{ - 7}}{H_{\max }}}} $ | (4) |
式中,Hmax为探空仪所记录的最高高度,φ为大地纬度,P(Hmax)为层顶大气压。
为了获取统计意义上的结论,选择尽量长的时间序列来评估模型的精度。GPT2_1w、GPT2_5w和IGGtrop模型是相对固定的经验模型,本文采用中国区域6 a(2010-01-01~2015-12-31)的探空数据计算的ZTD来评估这3种模型的精度。在进行精度评估前需要进行预处理,包括剔除高度过低的探空数据及剔除数据不连续的测站。经过预处理后,有85个测站的数据可用,站点分布相对比较均匀。
由于GTPs模型是2017-11正式发布的,且该模型是时变模型,目前尚不能获取长时间序列的数据,本文将采用1个月(2017-11-24~12-24)的探空数据来验证比较该模型的精度。GTPs模型的最大格网尺寸为267.5 km×222.6 km,最小尺寸为222.6 km×163.6 km,按照120 km的距离搜索策略,有部分区域无法被覆盖。由于格网点不一定是该区域的地形特征点,限定1.5 km高差的搜索策略也会导致一些地面站无法应用。经实验,按照水平距离180 km内的格点进行插值,可以保证地面站全部被覆盖且精度不会有较大变化。按照新的插值方法,有10个探空站无法解算出ZTD,主要是因为这些探空站附近GNSS基准站太少,无法提供有效的GTPs产品。随着中国地壳观测网络的不断建设,GNSS测站数量增加,该问题会得到很好的解决。经过处理后,最终得到的可用站点数为75个,除西南地区外,站点分布比较均匀。
本文采用平均bias和RMS来评估各模型精度,具体计算见文献[10]。
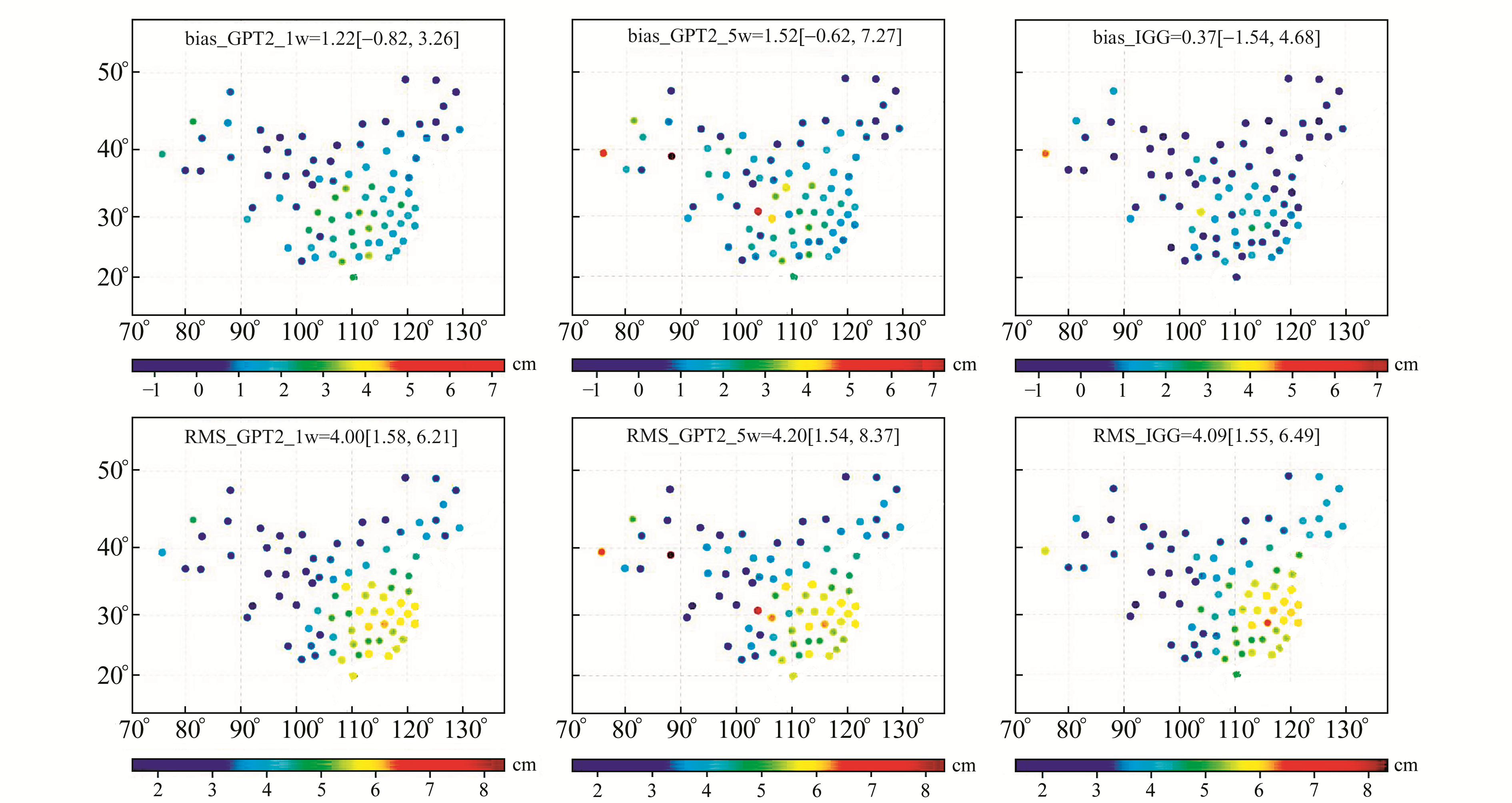
3 研究结果与分析 3.1 GPT2_1w、GPT2_5w和IGGtrop模型对比基于前文的数据和方法,对所有测站3种模型的平均bias和RMS进行统计,中国区域的平均结果和取值区间如图 1所示。从图 1可以看出,3种模型的平均RMS数值相当,为4.0~4.2 cm,但是从取值区间来看,GPT2_5w模型明显存在偏差较大的测站;3种模型的平均bias存在明显的差别,IGGtrop模型最小,为0.37 cm,GPT2_1w和GPT2_5w模型均超过1 cm,GPT2_5w模型最大,为1.52 cm,说明这2种模型在中国区域存在明显的正偏差;从bias分布图中可以看出,GPT2_1w和GPT2_5w模型在西北部以负向偏差为主,东南部以正向偏差为主;从RMS分布图中可以看出,3种模型在西部地区精度(1~3 cm)整体优于东部(4~6 cm),东南部地区精度最差(超过6 cm)。造成这种现象的原因是东南沿海比内陆水汽含量丰富,湿延迟变化相对剧烈,经验模型难以准确估计。
|
图 1 GPT2_1w、GPT2_5w和IGGtrop模型在中国区域的ZTD平均bias和RMS Fig. 1 Mean bias and RMS values of the GPT2_1w, GPT2_5w and IGGtrop models over China area |
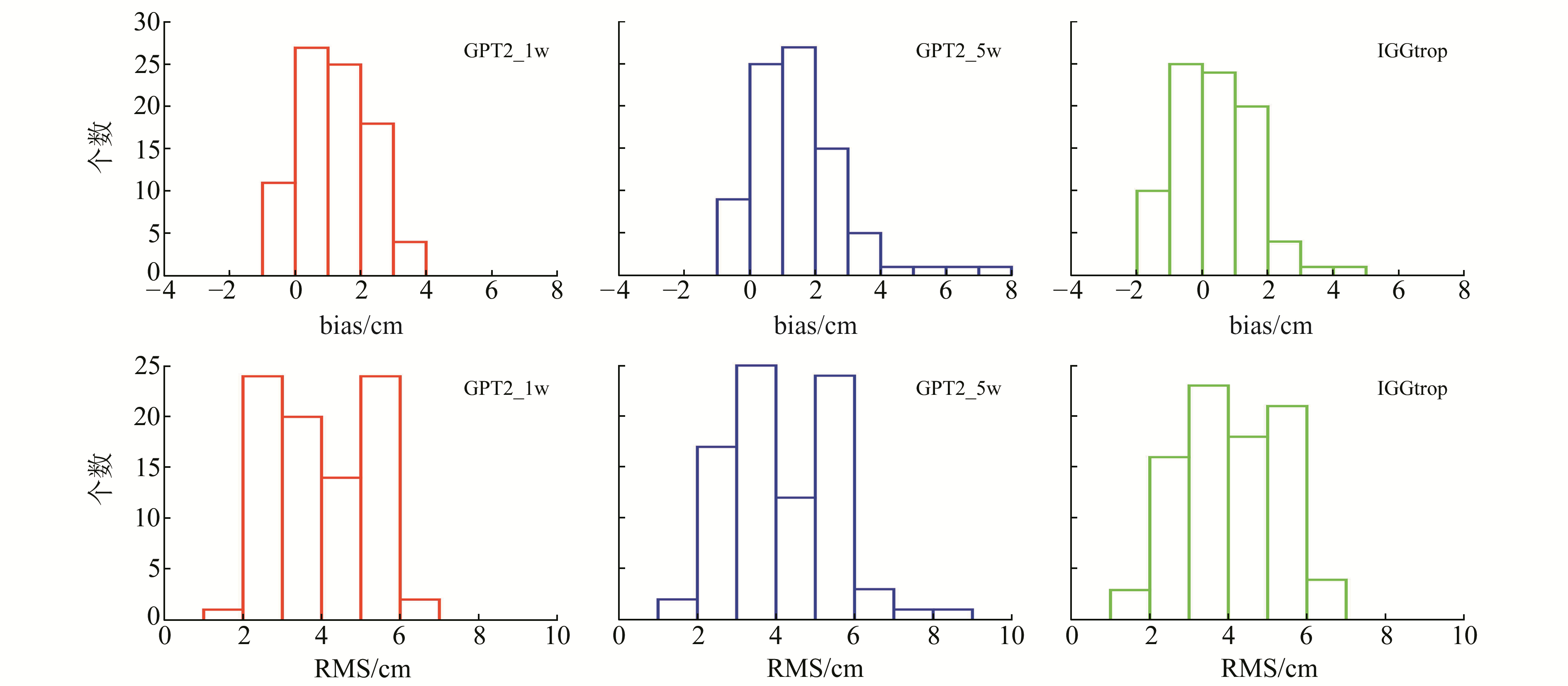
对不同模型的平均bias和RMS进行直方图统计,结果如图 2所示。从bias统计结果中可以看出,3种模型的偏差集中在-2~4 cm,IGGtrop模型分布适中,GPT2_1w模型和GPT2_5w模型明显存在1 cm左右的系统性偏差,GPT2_5w模型有一些站bias较大,超过4 cm。从RMS统计结果中可以看出,3种模型的平均RMS集中在2~6 cm。
|
图 2 GPT2_1w、GPT2_5w和IGGtrop模型平均bias和RMS直方图 Fig. 2 Histogram of mean bias and RMS for the GPT2_1w, GPT2_5w and IGGtrop models |
这3种模型在大部分测站上的bias和RMS差异在1 cm之内,表现出较好的一致性,其中差异较大的51777、56187和51709测站统计数据如表 1所示。可以看出,这3个测站高程相对较高,且主要分布在中西部,分辨率相对较高的GPT2_1w模型精度明显优于GPT2_5w模型和IGGtrop模型。这可能是因为在海拔较高的区域,对流层变化比较复杂,空间分辨率相对较低的模型无法反映部分区域ZTD的实际分布。不同分辨率的模型所包含的参数量不同,占用的存储空间也各不相同。在不考虑存储空间的情况下,应选择分辨率较高的模型,在中国东部地区可以选择分辨率相对较低的模型,在中国西部地区应选择分辨率相对较高的GPT2_1w模型。
|
|
表 1 精度差异较大测站的统计结果 Tab. 1 Accuracy statistical results of quite different stations |
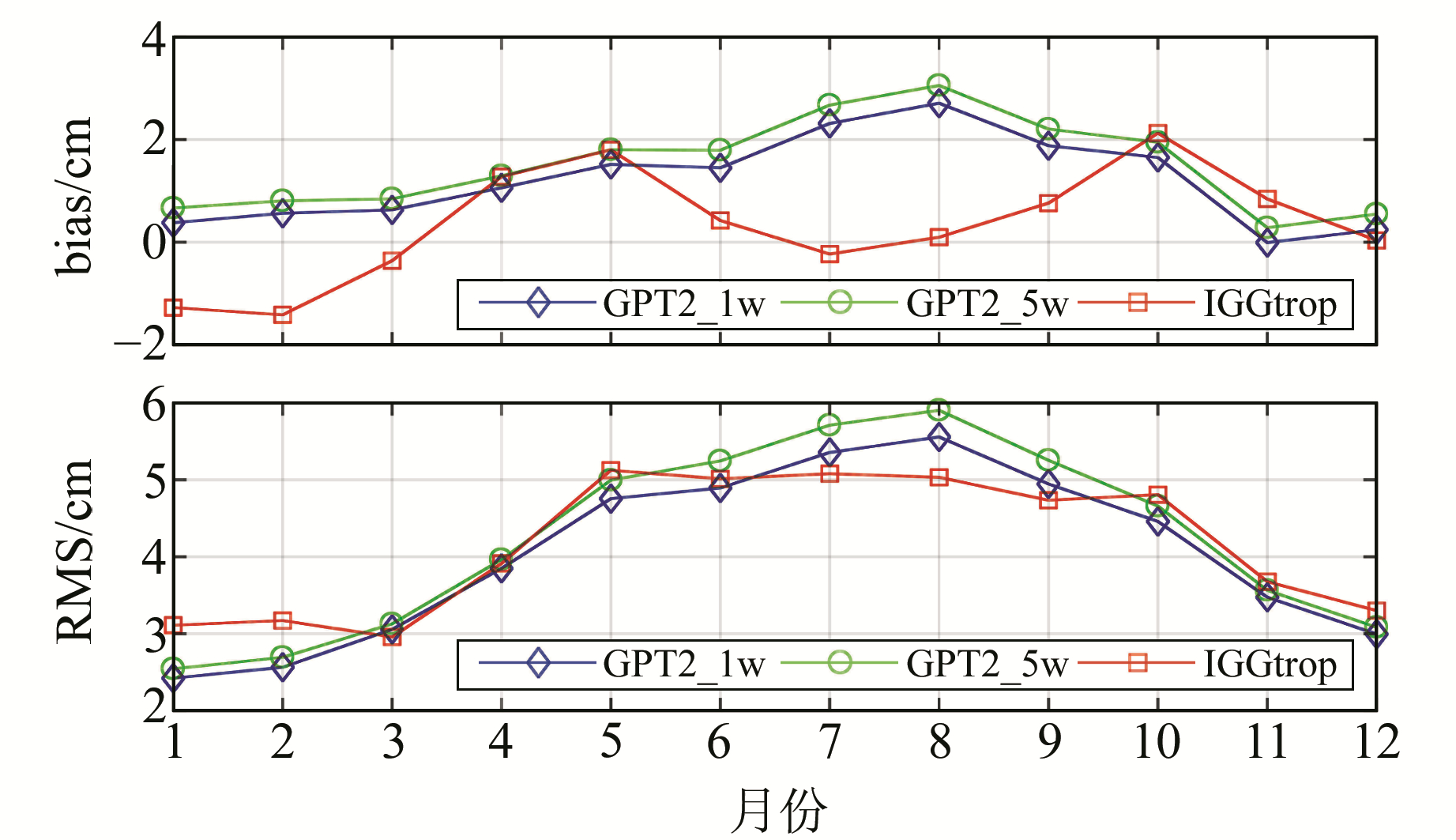
统计所有测站在不同月份的平均bias和RMS,得到图 3。从bias图可以看出,GPT2w模型的bias以正偏差为主,在8月份达到最大,GPT2_1w模型较GPT2_5w模型有2 mm整体偏差;IGGtrop模型正负偏差交替,总体上正偏差居多;IGGtrop模型冬季偏差比GPT2w模型大,可能是因为建模时未考虑ZTD的0.5 a周期变化。从RMS图中可以看出,3种模型在5~10月份精度为4~6 cm,其他月份精度在3 cm左右,这可能是由于夏季水汽分布变化相对较大,湿延迟估计不准确所致。
|
图 3 GPT2_1w、GPT2_5w和IGGtrop模型不同月份的精度 Fig. 3 ZTD accuracy for the GPT2_1w, GPT2_5w and IGGtrop models with respect to time |
由于GPT2_1w模型精度明显优于GPT2_5w模型,下文只讨论GPT2_1w模型。目前大部分的统计研究是基于地面站,对于飞行器定位导航中ZTD改正精度的分析相对较少。探空数据可以计算高空中的ZTD,因此可以采用探空数据进行相应的分析。根据探空数据,对ZTD取对数后在高程方向作线性插值,得到从地面到24 km高空、间隔为100 m的ZTD序列,以此为真值来评估这2种模型。
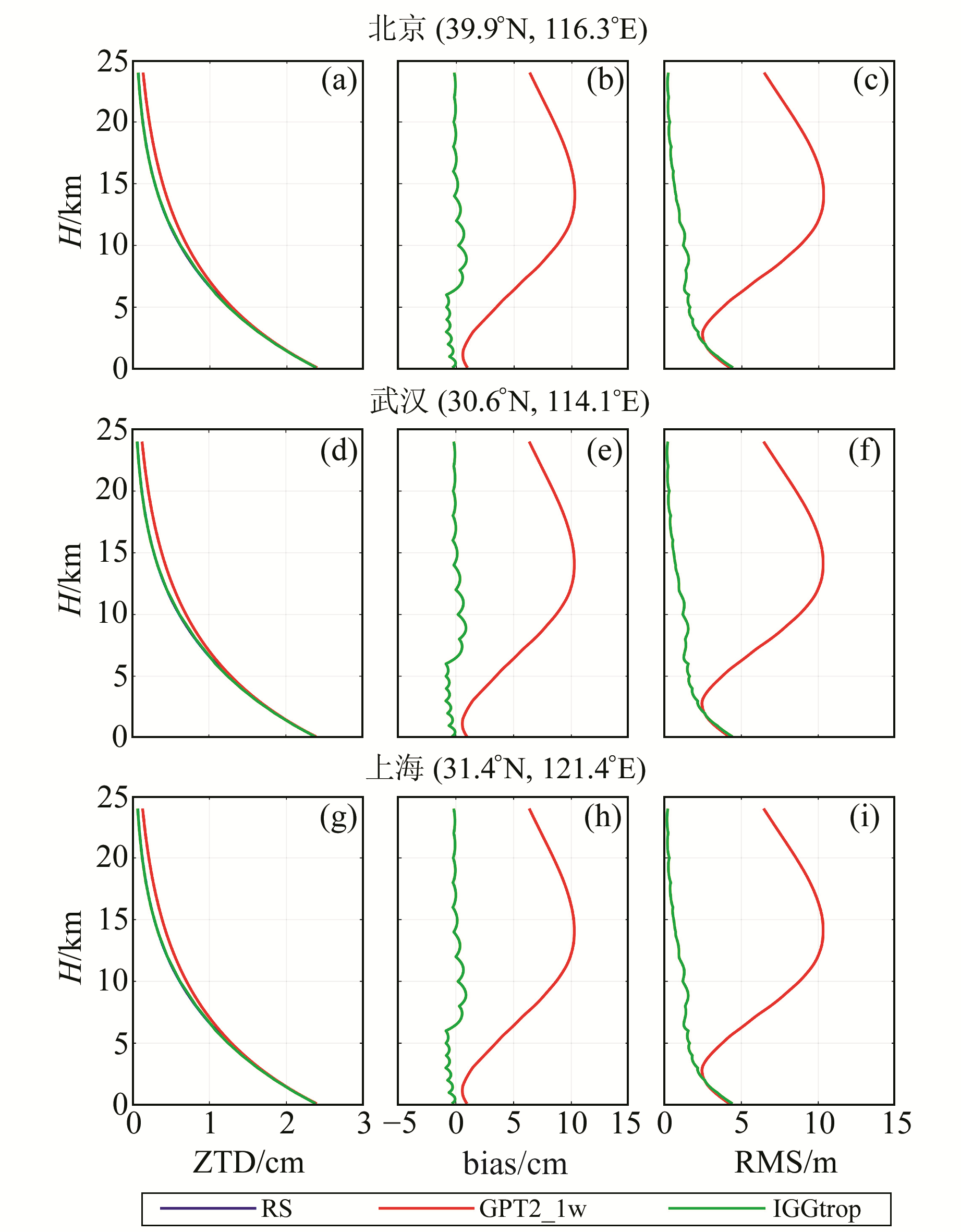
由于篇幅所限,仅以北京、武汉和上海站来进行说明。统计结果如图 4所示,其中图 4(a)、4(d)和4(g)分别为探空数据、GPT2_1w模型和IGGtrop模型在不同高度计算的平均ZTD分布图,图 4(b)、4(e)和4(h)为bias分布图,图 4(c)、4(f)和4(i)为RMS分布图。从ZTD分布图可以看出,ZTD随着高度的增加近似呈指数递减。图 4(a)、4(d)、4(g)中看不到探空数据的蓝色线,是因为从地面到24 km高空,IGGtrop模型计算的ZTD分布与探空数据计算的结果基本重合。对于IGGtrop模型,从地面到24 km高度bias始终在0附近波动,偏差在2 cm之内,其精度随高度增加而提高;对于GPT2_1w模型,从地面到3 km高度bias保持在2 cm之内,精度随高度增加而提高,从3 km到24 km高度bias和RMS随着高度升高先增大后减小,在13 km左右达到最大,约为10 cm,在24 km高度处bias仍超过5 cm。总体来说,从地面到3 km高度,IGGtrop模型和GPT2_1w模型精度相当,从3 km到24 km高度IGGtrop模型精度明显优于GPT2_1w模型。其他测站与该图特征一致,不同的是bias极大值所在的高度为13~18 km,bias极大值的范围为8~12 cm。
|
图 4 北京、武汉和上海站不同高度处的平均ZTD及精度统计 Fig. 4 Mean ZTD and accuracy statistical results at different heights of Beijing, Wuhan and Shanghai |
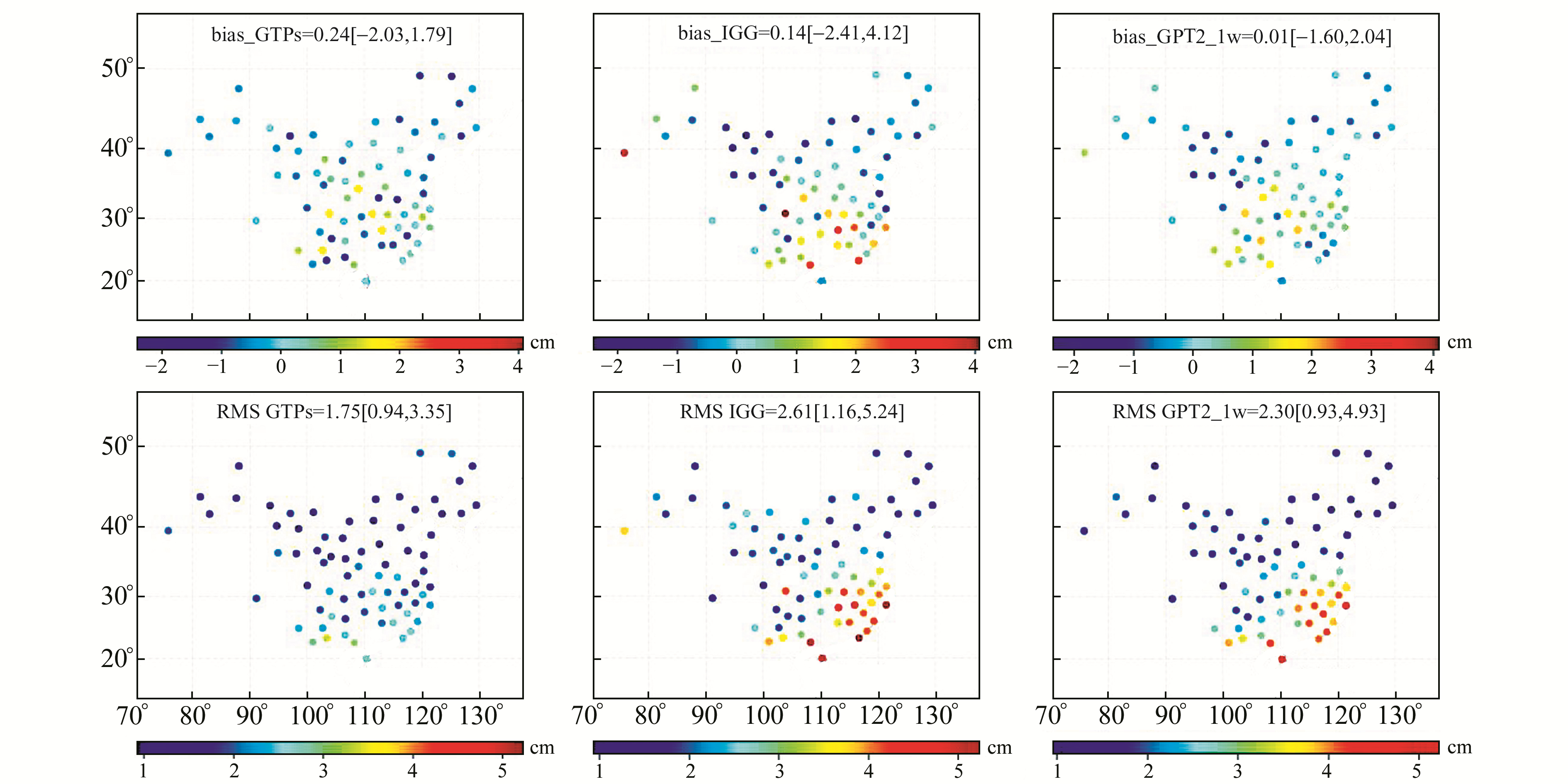
GPT2_1w模型、IGGtrop模型和GTPs模型2017-12的精度统计结果如图 5所示。对比图 3和图 5可以看出,GPT2_1w模型和IGGtrop模型2017-12的精度与2010~2015年所得的12月平均精度基本一致,说明采用75个测站评定精度是可靠的,除IGGtrop模型有较大bias外,其他模型bias均小于3 cm。GTPs模型修正效果明显优于其他2种模型,GPT2_1w模型精度略优于IGGtrop模型。
|
图 5 GTPs、IGGtrop和GPT2_1w模型在中国区域的ZTD平均bias和RMS(2017-12) Fig. 5 Mean bias and RMS values o for the GTPs、IGGtrop and GPT2_1w models over China area in December 2017 |
从图 5可以看出,GPTs模型bias分布较均匀,RMS随纬度的增加而减小,在东南沿海区域精度(2~3 cm)明显优于GPT2_1w模型和IGGtrop模型(3~5 cm),除了56985测站(23.4°N,103.4°E)精度超过3 cm,其他测站精度均优于3 cm,可能是由于用于插值计算的格点与测站距离较远,两地的ZTD相关性较低。随着GNSS基准网的不断加密,GTPs模型分辨率有望提高,精度也会随之提高。
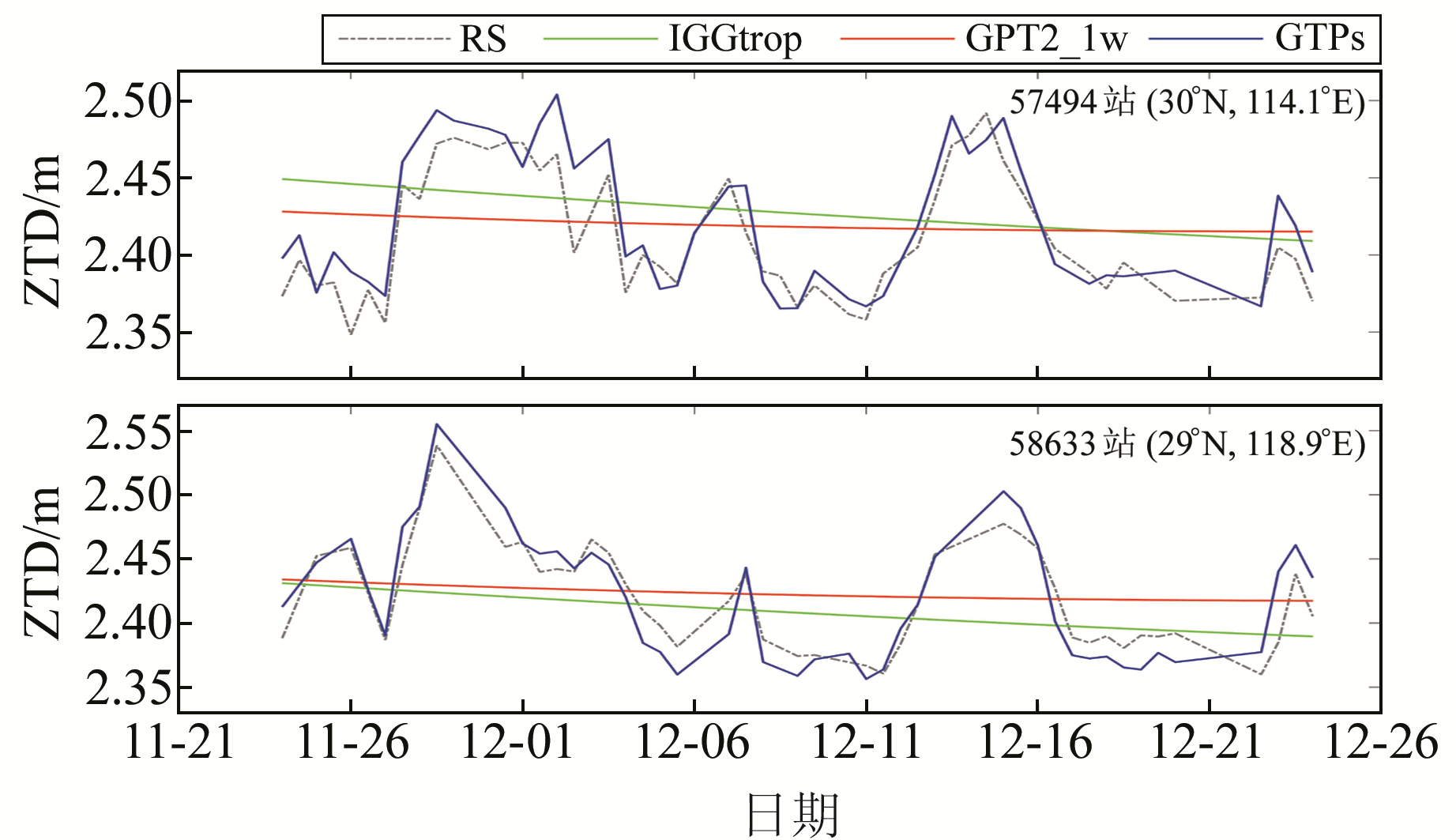
这3种模型精度的明显差异与建模的方法有很大关系。GTPs模型时间分辨率高,可以反映出ZTD短周期的变化,GPT2_1w模型考虑了气象参数的1 a周期变化和0.5 a周期变化,IGGtrop模型在赤道区域之外只考虑了ZTD的1 a周期变化。由于篇幅有限,仅以精度差异较大的东南沿海57494测站(30.6°N,114.1°E)和58633测站(29.0°N,118.9°E)进行说明。2个测站不同模型的ZTD序列如图 6所示,可以看出,ZTD在短时间内变化显著,传统的模型只考虑了1 a周期或0.5 a周期变化,并没有考虑ZTD的短周期特性,高时间分辨率的GTPs模型克服了这一点,利用GTPs模型可有效提高实时定位的精度与速度。
|
图 6 57494站和58633站不同模型的ZTD时间序列(2017) Fig. 6 Time series of ZTD of different models at 52533 and 58633 stations (2017) |
实时应用中,除了精度之外,还涉及模型计算的复杂程度、基础数据的存储及实时获得的可行性等多方面问题。各模型的实时应用性能统计如表 2所示,考虑到GTPs模型所服务的区域为16°~54°N、70~135°E,表中的参数量仅包含该区域。从前文可知,GTP2_1w、GPT2_5w、IGGtrop和GTPs模型在用户端的计算复杂程度虽略有区别,但对于现有计算机性能来说,并不会影响时效性。从表 2可以看出,高分辨率的GPT2_1w模型参数量远超过GPT2_5w模型,在同等分辨率的情况下,采用ZTD进行建模的IGGtrop模型和GTPs模型,参数量小于直接用气象资料所构建的GPT2w模型;GPT2w模型和IGGtrop模型的参数可存储在本地,而GTPs模型的参数则需要通过网络实时接收,如果按照float类型计算存储量,每30 s需要消耗2 160 B流量,会加重通信负担。GTPs模型精度虽高,但其依赖于外部数据源和通信环境,当分析中心无法解算出有效模型参数或通信出现故障时,将无法正常使用,而传统的经验模型则不受限制,随时随地可以使用。建议用户在实际应用中,根据精度、存储空间和网络情况选择模型。
|
|
表 2 GTP2_1w、GPT2_5w、IGGtrop和GTPs模型在中国区域实时应用性能统计 Tab. 2 Real-time application performance statistics of GTP2_1w, GPT2_5w, IGGtrop and GTPs model over China |
本文针对格网对流层天顶延迟模型GPT2w、IGGtrop和GTPs,采用探空数据分析各个模型在中国区域的适用性,得出如下结论:
1) GPT2_1w、GPT2_5w和IGGtrop模型在地表附近平均精度相当,为4.0~4.2 cm,但由于各模型分辨率不同,GPT2_5w模型和IGGtrop模型在中西部部分区域可能会产生异常偏差,在不考虑数据存储空间的情况下,用户应尽可能选择高分辨率的GPT2_1w模型。在中西部地区应选择高分辨率的GPT2_1w模型,在东南沿海地区可选择分辨率相对较低的GPT2_5w模型和IGGtrop模型。这些模型在西部地区精度优于东部,东南沿海精度最差,夏季精度明显低于冬季。GPT2w模型存在明显系统性偏差,在西北区域为负、东南区域为正。在使用时可以根据区域的不同,在总延迟上增加一个常数来减弱误差。
2) 在3 km高度以上,IGGtrop模型的ZTD修正效果明显优于GPT2w模型。对于飞行器导航定位,建议选择IGGtrop模型来改正对流层延迟误差。从地面到3 km高度,IGGtrop模型和GPT2_1w模型精度相当,且随高度增加精度提高;从3 km到24 km高度,IGGtrop模型精度随高度增加而提高,GPT2_1w模型随高度增加先降低后略微改善。
3) GTPs模型可以较好地反映ZTD在短周期内的变化,冬季平均精度可达1.8 cm,大多数区域偏差优于3 cm,尤其在东南沿海ZTD变化剧烈的区域,精度明显优于传统的经验模型。但该模型需要得到授权才可以获取,且依赖外部的数据源,目前有部分区域无法应用。随着GNSS基准站网的不断加密,GTPs模型的精度和可用性会得到逐步改善,从而更好地为PNT用户服务。另外,目前GTPs产品的覆盖时间有限,后续还会利用更长时间序列的模型数据对其精度进行分析。
| [1] |
Chen B Y, Liu Z Z. A Comprehensive Evaluation and Analysis of the Performance of Multiple Tropospheric Models in China Region[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 663-678 DOI:10.1109/TGRS.2015.2456099
(  0) 0) |
| [2] |
戴吾蛟, 陈招华, 匡翠林, 等. 区域精密对流层延迟建模[J]. 武汉大学学报:信息科学版, 2011, 36(4): 392-396 (Dai Wujiao, Chen Zhaohua, Kuang Cuilin, et al. Modeling Regional Precise Tropospheric Delay[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 392-396)
(  0) 0) |
| [3] |
Zhang H X, Yuan Y B, Li W, et al. Assessment of Three Tropospheric Delay Models (IGGtrop, EGNOS and UNB3m) Based on Precise Point Positioning in the Chinese Region[J]. Sensors, 2016, 16(1): 122 DOI:10.3390/s16010122
(  0) 0) |
| [4] |
Leandro R F, Langley R B, Santos M C. UNB3m_pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques[J]. GPS Solutions, 2007, 12(1): 65-70
(  0) 0) |
| [5] |
Penna N T, Dodson A H. Assessment of EGNOS Tropospheric Correction Model[J]. Journal of Navigation, 2001, 54(1): 37-55 DOI:10.1017/S0373463300001107
(  0) 0) |
| [6] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions, 2014, 19(3): 433-441
(  0) 0) |
| [7] |
Schüler T. The TropGrid2 Standard Tropospheric Correction Model[J]. GPS Solutions, 2014, 18(1): 123-131 DOI:10.1007/s10291-013-0316-x
(  0) 0) |
| [8] |
Li W, Yuan Y B, Ou J K, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(17): 2132-2139 DOI:10.1007/s11434-012-5010-9
(  0) 0) |
| [9] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227 (Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227)
(  0) 0) |
| [10] |
Zhang H X, Yuan Y B, Li W, et al. A Grid-Based Tropospheric Product for China Using a GNSS Network[J]. Journal of Geodesy, 2017(5): 1-13
(  0) 0) |
| [11] |
Zhou C C, Peng B B, Li W, et al. Establishment of a Site-Specific Tropospheric Model Based on Ground Meteorological Parameters over the China Region[J]. Sensors, 2017, 17(8): 1722 DOI:10.3390/s17081722
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39

