2. 中国科学院大学,北京市玉泉路19号甲,100049
国际全球导航卫星系统服务(IGS)自1994年起对外提供高精度的全球导航卫星系统(GNSS)产品,为科学、教育和商业应用提供精确的全球参考框架。过去,由于实时产品的稳定性和精度不高,高精度应用主要依赖事后产品。随着短延时或无延时应用需求的日益增长,实时GNSS产品已引起越来越多的关注。实时卫星钟差是IGS产品的重要组成部分,是实现实时精密单点定位(PPP)的关键要素,同时也可以为卫星钟的性能监测提供参考依据。
IGS于2007年号召多个国际分析中心参与实时飞行项目(RTPP),该项目强调实时卫星钟差的重要性[1]。2010年初,RTPP开始对外提供IGS01 / IGC01的GPS实时产品。2011-08 IGS实时工作组宣布RTPP已具备初步运行能力,可提供连续的GNSS数据流和实时轨道及钟差产品,并于2012年正式提供实时高精度GPS卫星轨道和钟差产品[2]。目前,多达10个国际实时分析中心(RTAC)可提供GPS或多GNSS实时轨道和钟差产品,其中,GPS产品由欧洲空间局的空间操作中心(ESA / ESOC)进行综合后对外播发,其公布的均方根误差为0.3 ns,标准差为0.12 ns。
GPS系统自上世纪成立以来,经过多年的改进和完善,已具备成熟的全球服务能力。随着RTPP和多GNSS实验与试点项目(MGEX)技术的发展,GNSS实时应用的优势[3-6]愈发突出,实时产品受到越来越多的关注。
目前,已有大量专家学者针对GPS实时钟差估计开展了相关研究[7-13]。实时卫星钟差估计常见的算法包括非差算法、历元差分算法及混合差分算法。本文基于Ge等[7]提出的混合差分算法,从待估参数数量出发,提出一种改进的混合差分算法。该算法在原方法仅对相位观测数据实施历元差分处理的基础上,对伪距和相位观测数据增加了星间差分处理,使得待估参数仅剩卫星钟差参数和对流层参数,不仅便于算法的实现,还可以满足高频率、高精度的解算需求。
1 混合差分算法卫星钟差估计采用无电离层的线性组合观测值,用以消除电离层延迟一阶项。实时钟差估计中,改进的混合差分处理分为:1)载波相位部分,采用历元间差分和星间差分处理;2)伪距部分,采用星间差分处理。
1.1 相位处理部分对于双频接收机,无电离层线性组合的相位观测方程如下:
| $ \begin{array}{l} L_{{\rm{IF}}, r}^s\left( i \right) = \rho _r^s\left( i \right) + m_r^s\left( i \right) \cdot {T_r}\left( i \right) + c \cdot {\rm{d}}{t_{{\rm{IF}}, r}}\left( i \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;c \cdot {\rm{d}}t_{{\rm{IF}}}^s\left( i \right) + N_{{\rm{IF}}, r}^s + {\varepsilon ^s}\left( i \right) \end{array} $ | (1) |
式中,L为载波相位观测值,上标s为卫星,下标r为接收机,IF为无电离层的标志,i为历元号,ρ为接收机和卫星相位中心之间的几何距离,m为对流层投影函数,T为天顶对流层延迟(zenith total delay,ZTD)参数,c为真空中的光速,dtIF, r和dtIFs分别为无电离层的接收机和卫星钟差,NIF, rs为无电离层模糊度参数,ε为无电离层的观测噪声。
处理载波相位时,首先对观测值进行历元间差分和星间差分处理。相邻历元间差分将消除模糊度参数NIF, rs,星间差分将消除接收机钟差dtIF, r(i)。通常选择当前解算历元中高度角最大的卫星作为参考星。GPS历元差分和星间差分载波相位观测方程如下:
| $ \begin{array}{l} \Delta L_{{\rm{IF}}, r}^{s, {\rm{ref}}}\left( i \right) = \Delta \rho _r^{s, {\rm{ref}}}\left( i \right) + \Delta m_r^{s, {\rm{ref}}}\left( i \right) \cdot {T_r}\left( i \right) - \\ \;\;c \cdot \Delta {\rm{d}}t_{{\rm{IF}}}^s\left( i \right) + c \cdot \Delta {\rm{d}}t_{{\rm{IF}}}^{{\rm{ref}}}\left( i \right) + \Delta {\varepsilon ^{s, {\rm{ref}}}}\left( i \right) \end{array} $ | (2) |
式中,Δ为当前历元i与之前某个历元i'的观测值作差,ref为历元i作差分时的参考星。
由于固定了卫星和接收机位置,式(2)中的待估参数只有Tr、ΔdtIFs和ΔdtIFref。为避免式(2)中其他卫星与参考星钟差之间的秩亏问题,解算时在历元i引入一个钟差基准约束条件:
| $ \mathop \sum \limits_{s = 1}^m \Delta {\rm{d}}t_{{\rm{IF}}}^s\left( i \right) = \mathop \sum \limits_{s = 1}^m \Delta {\rm{bc}}{{\rm{k}}^s}\left( i \right) $ | (3) |
式中,s为卫星号,m为解算卫星的总数,bck为广播钟差值。
解算式(2)和式(3),可得天顶对流层参数Tr和卫星钟差历元间变化值ΔdtIFs。
1.2 伪距处理部分类似于相位处理部分,伪距观测方程如下:
| $ \begin{array}{l} P_{{\rm{IF}}, r}^s\left( i \right) = \rho _r^s\left( i \right) + m_r^s\left( i \right) \cdot {T_r}\left( i \right) + \\ \;c \cdot {\rm{d}}{t_{{\rm{IF}}, r}}\left( i \right) - c \cdot {\rm{d}}t_{{\rm{IF}}}^s\left( i \right) + {e^s}\left( i \right) \end{array} $ | (4) |
式中,P为伪距观测值,e为无电离层伪距观测噪声。由相位观测方程解得钟差历元间变化值ΔdtIFs(i)之后,历元i处的卫星钟差可表示为:
| $ {\rm{d}}t_{{\rm{IF}}}^s\left( i \right) = {\rm{d}}t_{{\rm{IF}}}^s\left( 0 \right) + \mathop \sum \limits_{k = 1}^i \Delta {\rm{d}}t_{{\rm{IF}}}^s\left( k \right) $ | (5) |
式中,dtIFs(0)为卫星s的初始时刻钟差,k为历元计数标识。此时,ρrs(i)、Tr(i)和ΔdtIF(k)组合成固定值:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\rho _r^{s'}\left( i \right) = \\ \rho _r^s\left( i \right) + m_r^s\left( i \right) \cdot {T_r}\left( i \right) + \mathop \sum \limits_{k = 1}^i \Delta {\rm{d}}t_{{\rm{IF}}}^s\left( k \right) \end{array} $ | (6) |
处理伪距观测值时,首先将式(6)代入式(4),之后实施星间差分,用以消除接收机钟差参数dtIF, r。新的差分观测方程为:
| $ \begin{array}{l} P_{{\rm{IF}}, r}^{s, {\rm{ref}}}\left( i \right) = \rho _r^{s, {\rm{ref}}}{'}\left( i \right) - c \cdot {\rm{d}}t_{{\rm{IF}}}^s\left( 0 \right) + \\ \;\;\;\;\;\;\;c \cdot {\rm{d}}t_{{\rm{IF}}}^{{\rm{ref}}}\left( 0 \right) + {e^{s, {\rm{ref}}}}\left( i \right) \end{array} $ | (7) |
同样,式(7)在其他卫星与参考卫星钟差之间存在秩亏问题。为消除该问题,选择当前历元所有卫星的广播钟差作为基准,增加约束条件:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\mathop \sum \limits_{s = 1}^m {\rm{d}}t_{{\rm{IF}}}^s\left( 0 \right) = \\ \mathop \sum \limits_{s = 1}^m \left[ {{\rm{bc}}{{\rm{k}}^{\rm{s}}}\left( i \right) - \mathop \sum \limits_{k = 1}^i \Delta {\rm{d}}t_{{\rm{IF}}}^s\left( k \right)} \right] \end{array} $ | (8) |
实时钟差估计算法的实现过程主要分为4个步骤:
1) 估计ZTD参数。通过处理载波相位方程式(2)和(3),估计ZTD。该过程中,算子Δ中的历元i'与历元i的间隔设置为300 s,避免出现当2个历元非常接近时,由于式(2)中Tr(i)的系数过小导致ZTD估值不准确的情况。顾及ZTD参数在1 h弧段内较为稳定,在1 h内视为常量,并使用当前历元前1 h的Tr均值作为当前历元的ZTD结果。
2) 估计钟差历元间变化参数。将1)中的ZTD结果Tr(i)的均值作为高权重的已知值引入,并通过解算载波相位方程式(2)和式(3),估计卫星钟差相邻历元间的变化值ΔdtIFs(i)。在该过程中,算子Δ中的历元i'被设置为i的前一历元,即此时i'与i之间的间隔为钟差产品的时间间隔。
3) 估计初始时刻卫星钟差参数。在引入1)与2)所生成的ZTD值Tr(i)和钟差历元间变化值ΔdtIFs(i)之后,未知参数仅剩卫星的初始时刻钟差dtIFs(0)。通过解算伪距方程式(7)和式(8),生成初始时刻卫星钟差。为获得准确的初始时刻钟差,对卫星s选取初始时刻后1 h内各个历元解算的dtIFs(0)结果取平均,作为最终的初始时刻钟差,供式(5)使用。一旦卫星s的初始时刻钟差确定,将不会被轻易更新,除非数据出现长时间的缺失。
4) 预报用户接收时刻钟差。由于数据的采集、解算及产品播发均存在一定的时间延迟,本步骤通过将钟差结果向外预报几个历元之后提供给用户,以解决该问题。考虑到卫星钟差历元间变化值较为稳定,各卫星均选取当前历元前1 h的钟差历元间变化均值,作为数据解算时刻i之后数10 s以内的卫星钟差历元间变化值。
利用2)~4)中解得的钟差历元间变化、初始时刻钟差及历元间变化均值,根据式(5)生成播发时刻所需的卫星钟差结果(图 1)。

|
图 1 实时钟差算法实现流程 Fig. 1 Flow chart of the real-time satellite clock offset estimation |
相较于旧的混合差分算法,改进后的算法在其基础上增加了星间差分处理,以消除接收机钟差。由于旧的混合差分算法中,待估参数包括接收机钟差,因此在数据预处理部分,需要利用伪距单点定位解算每个接收机各历元的接收机钟差近似值。改进的混合差分算法在消除了接收机钟差后,具备以下3个方面的优势:
1) 具有更少的待估参数,可以更高效地估计卫星钟差。假设某一历元中,卫星数为32,接收机数为50,则旧方法中待估参数有32个卫星钟差、50个接收机钟差和50个对流层延迟参数,共132个;改进的算法中待估参数有32个卫星钟差和50个对流层延迟参数,共82个。因此,改进后的算法具有更少的待估参数,可以提高方程的解算效率。
2) 无需实施伪距单点定位,减少了计算量。由于不需要计算接收机钟差,因此也不需要伪距单点定位来获取接收机钟差的近似值,进而减少了解算过程中的计算量。
3) 更加简单的数据质量控制方法。由于实施了新的混合差分处理,相位和伪距观测方程式(2)和式(7)仅剩卫星钟差和对流层延迟参数。此外,当式(2)中用作差分的2个历元非常接近(如5 s)时,Δmrs, ref(i)将变得非常小,绝大多数(99%)小于0.01,这样,在代入卫星钟差近似值后,可直接根据残差的异常值进行数据质量控制。
2 数据处理在数据处理过程中,选择68个可提供实时数据流的IGS跟踪站,其中可稳定接收到的跟踪站约55个,这些跟踪站均匀地分布于全球。选取2018-01-14~01-19作为测试时段,实施过程中除GPS PRN4号卫星处于非健康状态被剔除外,实际解算的卫星共31颗。
实时钟差估计中,使用法国国家空间研究中心(CNES)提供的实时轨道产品(ftp://ppp-wizard.net/products/)。该实时GPS卫星轨道在径向、切向和法向上的精度约为2~3 cm,对卫星钟差的精度影响约为0.1 ns[14-15],可以满足实时钟差及实时定位应用的需求。卫星钟差估计中,解算频率设置为5 s/次,对外提供5 s级更新的实时卫星钟差改正信息。由于实时数据流的滞后性,解算时刻设置为当前时刻前10 s,以保证能接收到与大部分测站相同时刻的数据。为保证播发的实时钟差方便用户使用,播发的钟差历元时刻设置为当前时刻后5 s,即解算时刻后15 s。
数据处理中,数据质量控制采取对单个历元进行残差剔除的方法。对于混合差分后的相位观测值,式(2)中只剩卫星钟差和对流层参数,且对流层系数Δmrs, ref(i)非常小(99%小于0.01),代入卫星钟差和对流层延迟近似值后,将残差绝对值大于3倍残差RMS的观测值当作粗差剔除。对于星间差分的伪距观测值,在代入相位部分解算的钟差变化和对流层延迟值后,式(7)仅剩初始时刻钟差,再代入近似值后,将残差绝对值大于3倍残差RMS的观测值当作粗差剔除。
3 结果验证实时卫星钟差利用改进的混合差分算法,依据实施步骤及其所述配置,实时对外播发钟差改正值,供用户接收使用,同时存储播发值用以评定精度。钟差结果采用2种方式进行评估:1)与事后钟差产品比较;2)实时用户实施动态PPP进行检验。
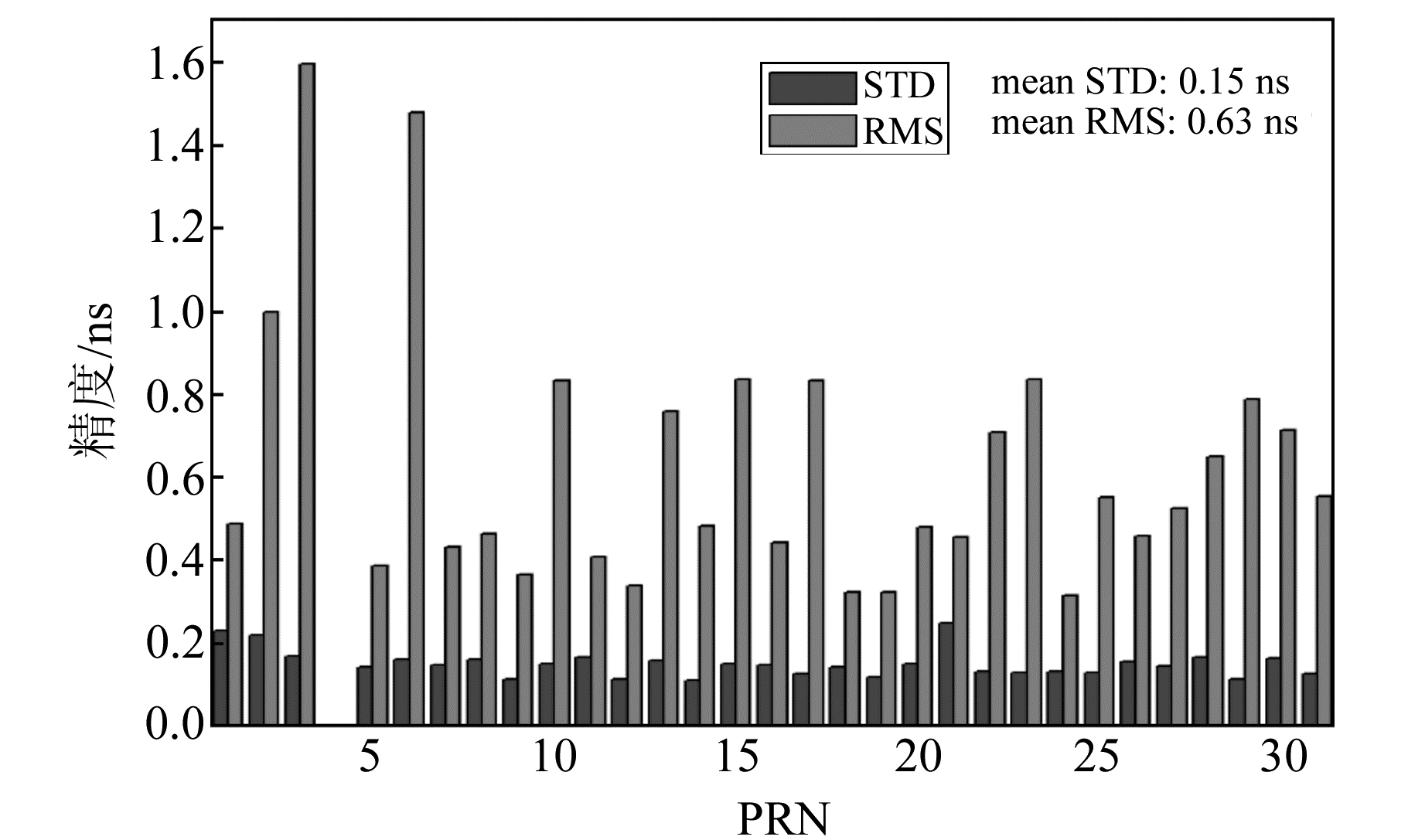
3.1 与事后钟差比较选取IGS快速钟差产品作为参考值,与实时卫星钟差进行比较。比较方法采用二次作差法[16],消除基准钟的影响。统计2018-01-14~01-19实时钟差产品精度,结果如图 2所示,横轴为卫星PRN序号,纵轴为各卫星对应统计值6 d的均值。
|
图 2 GPS实时卫星钟差与IGS快速钟差比较结果 Fig. 2 Statistic results of the comparison between generated clock and IGS rapid clock products |
图 2中3号和6号卫星的RMS较大,主要是由于在初始化过程中,有一小段时间接收到的3号和6号卫星数据流不稳定,导致初始时刻钟差估值较差。因此,稳定、连续的数据也是制约卫星钟差精度的重要因素。
由图 2可知,本系统生成的实时卫星钟差结果与最终结果比较的STD约为0.15 ns,RMS约为0.63 ns,与国际上公布的精度水平相当[15],理论上可提供cm级定位服务。因此,改进的混合差分算法可以满足实时卫星钟差产品的性能需求。
3.2 动态PPP验证动态PPP是直接检验钟差产品实际应用水平的工具。在动态PPP实施过程中,接收实时播发的卫星钟差改正信息,改正由卫星钟差产生的卫星至接收机的几何距离偏差。为检验实时钟差的定位水平,随机选取7个IGS跟踪站(图 3)于2018-01-18实施实时仿动态PPP。

|
图 3 用于实时动态PPP测试的测站 Fig. 3 Stations for real-time kinematic PPP testing |
将动态PPP结果与IGS提供的SINEX结果比较,统计东、北和垂直3个方向的RMS,结果如图 4所示。

|
图 4 2018-01-18各测站实时仿动态PPP结果在东、北和垂直3个方向的精度 Fig. 4 January 18, 2018, the accuracy of real-time kinematic PPP results in east, north and vertical directions |
由图 4可知,利用该实时卫星钟差产品可以实现东、北和垂直方向cm级的实时动态定位,从而证实该产品已经具备了提供实时cm级定位服务的能力。
4 结语GPS卫星实时钟差产品是提升实时导航和授时应用的重要参数。为简化钟差估计模型,提高实时钟差估计效率,本文提出一种改进的混合差分算法,该算法在常规混合差分算法的基础上,通过实施星间差分,进一步消除接收机钟差参数,将待估参数降到最少,不仅便于程序实现,还可以高效运算。在算法实现中,采用4个主要步骤,逐步获取ZTD、钟差历元间变化值、初始时刻钟差值和播发时刻钟差值。
在程序实际运行中,基于68个IGS跟踪站的实时数据流实施实时钟差估计,钟差结果与IGS事后产品进行比较,并运用动态PPP进行验证。结果显示,实时卫星钟差的STD约为0.15 ns,RMS约为0.63 ns。同时,动态PPP结果在东、北和垂直方向分别达到4.6 cm、4.0 cm和8.5 cm的水平,表明该实时钟差产品可以对外实时提供cm级的定位服务。因此,本文提出的实时卫星钟差估计方法及实施过程可行,提供的卫星钟差产品与国际产品水平相当[15],编制的软件已初步具备服务的能力。
本文仅依据GPS系统验证了该方法的可行性,但该方法是否适用于多系统联合处理,能否提供多GNSS实时卫星钟差,还有待进一步开展相关的研究工作。
| [1] |
Weber G, Mervart L, Lukes Z, et al. Real-Time Clock and Orbit Corrections for Improved Point Positioning via NTRIP[C].ION GNSS, Fort Worth, 2007
(  0) 0) |
| [2] |
Caissy M, Agrotis L, Weber G, et al. The International GNSS Real-Time Service[J]. GPS World, 2012, 23(6): 52-58
(  0) 0) |
| [3] |
Dai Z Q, Zhao Q L, Lü Y F, et al. The Wide- and Local-Area Combined GNSS Real-Time Precise Positioning Service System and Products[C]. China Satellite Navigation Conference, Shanghai, 2017 https://link.springer.com/chapter/10.1007%2F978-981-10-4594-3_34
(  0) 0) |
| [4] |
Li X X, Ge M R, Dai X L, et al. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, Beidou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635 DOI:10.1007/s00190-015-0802-8
(  0) 0) |
| [5] |
Li X X, Dick G, Lu C X, et al. Multi-GNSS Meteorology: Real-Time Retrieving of Atmospheric Water Vapor from Beidou, Galileo, GLONASS, and GPS Observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(12): 6385-6393 DOI:10.1109/TGRS.2015.2438395
(  0) 0) |
| [6] |
Teferle N, Ding W W, Abraha K E, et al. Multi-GNSS Benefits to Real-Time and Long-Term Monitoring Applications[C]. IAG/CPGPS International Conference on GNSS+, Shanghai, 2016
(  0) 0) |
| [7] |
Ge M R, Chen J P, Douša J, et al. A Computationally Efficient Approach for Estimating High-Rate Satellite Clock Corrections in Realtime[J]. GPS Solutions, 2012, 16(1): 9-17 DOI:10.1007/s10291-011-0206-z
(  0) 0) |
| [8] |
Hauschild A, Montenbruck O. Kalman-Filter-Based GPS Clock Estimation for Near Real-Time Positioning[J]. GPS Solutions, 2009, 13(3): 173-182 DOI:10.1007/s10291-008-0110-3
(  0) 0) |
| [9] |
Zhang X H, Li X X, Guo F. Satellite Clock Estimation at 1 Hz for Realtime Kinematic PPP Applications[J]. GPS Solutions, 2011, 15(4): 315-324 DOI:10.1007/s10291-010-0191-7
(  0) 0) |
| [10] |
Laurichesse D, Cerri L, Berthias J P, et al. Real Time Precise GPS Constellation and Clocks Estimation by Means of a Kalman Filter[C]. ION GNSS, Nashville, 2013
(  0) 0) |
| [11] |
Zhang Q, Moore P, Hanley J, et al. Auto-BAHN: Software for Near Real-Time GPS Orbit and Clock Computations[J]. Advances in Space Research, 2007, 39(10): 1531-1538 DOI:10.1016/j.asr.2007.02.062
(  0) 0) |
| [12] |
Gong X P, Gu S F, Lou Y D, et al. An Efficient Solution of Real-Time Data Processing for Multi-GNSS Network[J]. Journal of Geodesy, 2018, 92(7): 797-809 DOI:10.1007/s00190-017-1095-x
(  0) 0) |
| [13] |
陈良, 胡志刚, 耿长江, 等. GNSS增强系统中精密实时钟差高频估计及应用研究[J]. 测绘学报, 2016, 45(增2): 12-21 (Chen Liang, Hu Zhigang, Geng Changjiang, et al. Study on a High-Frequence Multi-GNSS Real-Time Precise Clock Estimation Algorithm and Application in GNSS Augment System[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 12-21)
(  0) 0) |
| [14] |
Kazmierski K, Sošnica K, Hadas T. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-Time Precise Point Positioning[J]. GPS Solutions, 2018, 22(1): 11 DOI:10.1007/s10291-017-0678-6
(  0) 0) |
| [15] |
Wang Z Y, Li Z S, Wang L, et al. Assessment of Multiple GNSS Real-Time SSR Products from Different Analysis Centers[J]. ISPRS International Journal of Geo-Information, 2018, 7(3): 85 DOI:10.3390/ijgi7030085
(  0) 0) |
| [16] |
Agrotis L, Sanz P A, Dow J, et al. ESOC's RETINA System and the Generation of the IGS RT Combination[C]. IGS Workshop, Newcastle Upon Tyne, 2010
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39

