SWARM卫星由欧洲航天局(ESA)于2013-11-22成功发射,是ESA首个用于地球区域磁场信息探测的低轨卫星星座。SWARM包括3颗卫星,其中SWARM-A和SWARM-C卫星轨道高度为450 km,轨道倾角为87.4°,SWARM-B卫星轨道高度为530 km,倾角为88°,通过卫星星座特殊的空间分布,可以在地球磁场测量期间有效解决时空模糊度的问题[1]。3颗卫星均配备了精密的科学仪器,包括星载GPS接收机、加速度计、激光后向反射器等。SWARM卫星搭载的高精度加速度计,能够填补GRACE卫星退役后,新的探测卫星尚未发射的重力场监测空窗期[2]。学者们根据不同低轨卫星精密轨道恢复的高精度地球重力场均达到较好的效果[3-5]。因此,分析SWARM卫星不同方法的定轨精度可根据不同需要进行合理化选择,对后续科学工作的开展有着至关重要的作用。
星载GPS定轨是目前低轨卫星中最有效的定轨手段,这是因为GPS接收机可以提供连续的星载GPS数据,为轨道的确定提供有效的数据支撑。根据低轨卫星数据处理所采用的力学模型和观测数据的不同,将定轨方法分为运动学精密定轨、动力学精密定轨和简化动力学精密定轨。运动学法主要使用星载GPS观测数据进行定轨,不受力学模型的影响,特别是近年来星载GPS技术的不断发展,运动学精密定轨精度能达到cm级[6];动力学法作为传统的卫星定轨方法,通过建立力学模型,确定卫星的理论轨迹,最后根据实测数据改进卫星轨道,但由于太阳辐射压、地球辐射压、大气阻力等非保守力学模型难以精确测定,定轨精度有待提高[7]。Yunck等[8]在动力学法基础上创新地提出简化动力学法,其特点是将动力学轨道作为先验轨道,通过伪随机脉冲参数在滤波和平滑中的设置,对大气密度模型和太阳光压模型等进行优化,削弱非保守力摄动模型对轨道精度的影响,以此实现低轨卫星精密定轨的目的。
本文主要采用运动学和简化动力学方法,利用7 d非差星载GPS观测数据对SWARM卫星进行精密定轨,比较运动学轨道和简化动力学轨道的差异。将定轨结果与ESA发布的科学轨道进行外符合精度评定,分析2种方法的定轨精度,讨论IGS发布的快速星历、超快速星历对SWARM卫星简化动力学定轨的影响[9]。
1 基于星载GPS的SWARM卫星定轨方法 1.1 观测方程在星载GPS定轨中,可将误差源分为以下3类:1)与GPS卫星有关的误差,主要包括GPS天线相位中心偏差、GPS卫星钟差等;2)与传播路径有关的误差,主要包括电离层延迟、相对论效应等;3)与低轨卫星有关的误差,主要包括接收机钟差、接收机天线相位中心改正、天线缠绕改正等[10]。根据这些误差源,建立低轨卫星与GPS卫星之间的相位观测和伪距观测消电离层组合方程,分别为[5, 11]:
| $ {L_3} = \rho _{\rm{r}}^{\rm{s}} + c(\delta {t_{\rm{r}}} - \sigma {t^{\rm{s}}}) + {\sigma _{{\rho _{{\rm{rel}}}}}} + {\sigma _\rho }_{_{{\rm{wind - up}}}} + \lambda B + {\varepsilon _{{P_3}}} $ | (1) |
| $ {P_3} = \rho _{\rm{r}}^{\rm{s}} + c(\delta {t_{\rm{r}}} - \sigma {t^{\rm{s}}}) + {\sigma _{{\rho _{{\rm{rel}}}}}} + {\sigma _\rho }_{_{{\rm{wind - up}}}} + {\varepsilon _P}_{_3} $ | (2) |
式中,L3为载波相位观测值,P3为伪距观测值,
由于星载GPS观测得到的是GPS天线到接收机天线之间的距离,GPS卫星精密星历和LEO卫星精密轨道的坐标是以卫星质心为基准给出的,因此,在低轨卫星精密定轨的过程中,要加入GPS卫星和LEO卫星天线相位中心改正[12]。
1.2 简化动力学方法低轨卫星除了受到地心引力外,还受到潮汐摄动力、太阳光压力、多体摄动力和大气阻力等因素的影响,根据这些摄动模型建立的基本方程为[13]:
| $ \mathit{\boldsymbol{\ddot r}} = - \frac{{GM}}{{{\mathit{\boldsymbol{r}}^3}}}\mathit{\boldsymbol{r}} + {f_1}({t_1}, \mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\dot r}}, {q_1}, \cdots , {q_d}) $ | (3) |
式中,r、
假设先验轨道r0(t)和先验轨道参数pi0已知,动力学定轨可以看作是一个逐步改善轨道的过程。对r(t)进行泰勒级数展开,消去基本观测方程中的未知摄动力参数,对低轨卫星观测数据和其他相关参数作最小二乘处理,求得pi0的改正值,修正后的轨道表达式为[13]:
| $ \mathit{\boldsymbol{r}}\left( t \right) = {\mathit{\boldsymbol{r}}_0}\left( t \right) + \mathop \sum \limits_{i = 1}^n \frac{{\partial {\mathit{\boldsymbol{r}}_0}\left( t \right)}}{{\partial {p_i}}}({\mathit{\boldsymbol{p}}_i} - {\mathit{\boldsymbol{p}}_{{i_0}}}) $ | (4) |
式中,pi表示轨道参数,pi0为pi的先验值。
使用简化动力学方法进行卫星精密定轨与动力学法类似。不同的是,动力学法在定轨的过程中力学模型可能不精确,定轨精度随着模型误差的累积逐渐降低。简化动力学法将运动学法与动力法相结合,使用较少的力学模型,通过附加伪随机参数,对先验轨道进行参数化。通过预先时间历元的划分和先验标准差的设置,在星载GPS观测数据和动力学模型之间进行最优选权,在一次次迭代循环中筛选参数不断优化,轨道的质量不断改善。在低轨卫星轨道坐标的求解过程中,附加伪随机参数等过程噪声参数的优点是可以吸收动力学模型误差和没有被模型化的误差,进而提高简化动力学轨道的精度[14]。
2 解算策略 2.1 数据准备高精度的GPS卫星精密星历和卫星钟差是低轨卫星精密定轨的关键,本文主要采用CODE(center for orbit determination in Europe)中心提供的精密星历、30 s采样间隔的卫星钟差及地球自转参数文件。从ESA(https://earth.esa.int)下载2017-04-30~05-06共7 d采样间隔为1 s的星载GPS观测数据和卫星姿态数据,事后科学轨道也由ESA提供,采样间隔为10 s,轨道精度优于2 cm。精密定轨所使用的力学模型[15]如表 1所示。
|
|
表 1 SWARM卫星精密定轨所采用的标准模型 Tab. 1 The model standards adopted for SWARM precise orbit determination |
本文利用Bernese5.2软件对SWARM卫星定轨进行研究,运动学和简化动力学定轨技术路线如图 1所示。

|
图 1 SWARM定轨技术路线 Fig. 1 Technical route of SWARM precise orbit determination |
将解算的SWARM 3颗卫星运动学轨道与ESA发布的科学轨道进行对比,在RTN坐标系下进行分析,结果如图 2~4和表 2所示。
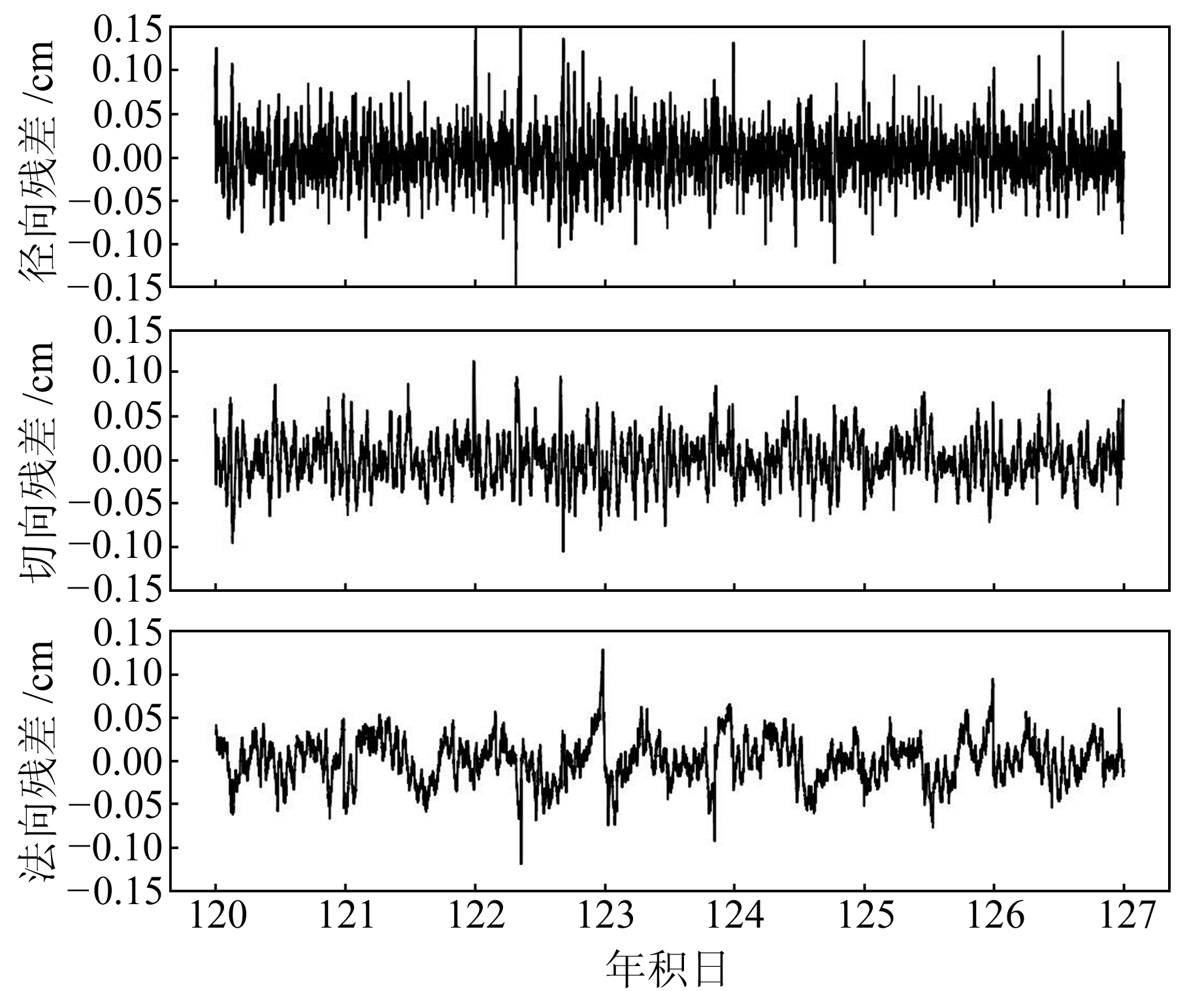
|
图 2 SWARM-A卫星年积日120~126的运动学轨道与ESA轨道差值 Fig. 2 The residuals between kinematic orbit and product released by ESA for SWARM-A during doy 120~126 |
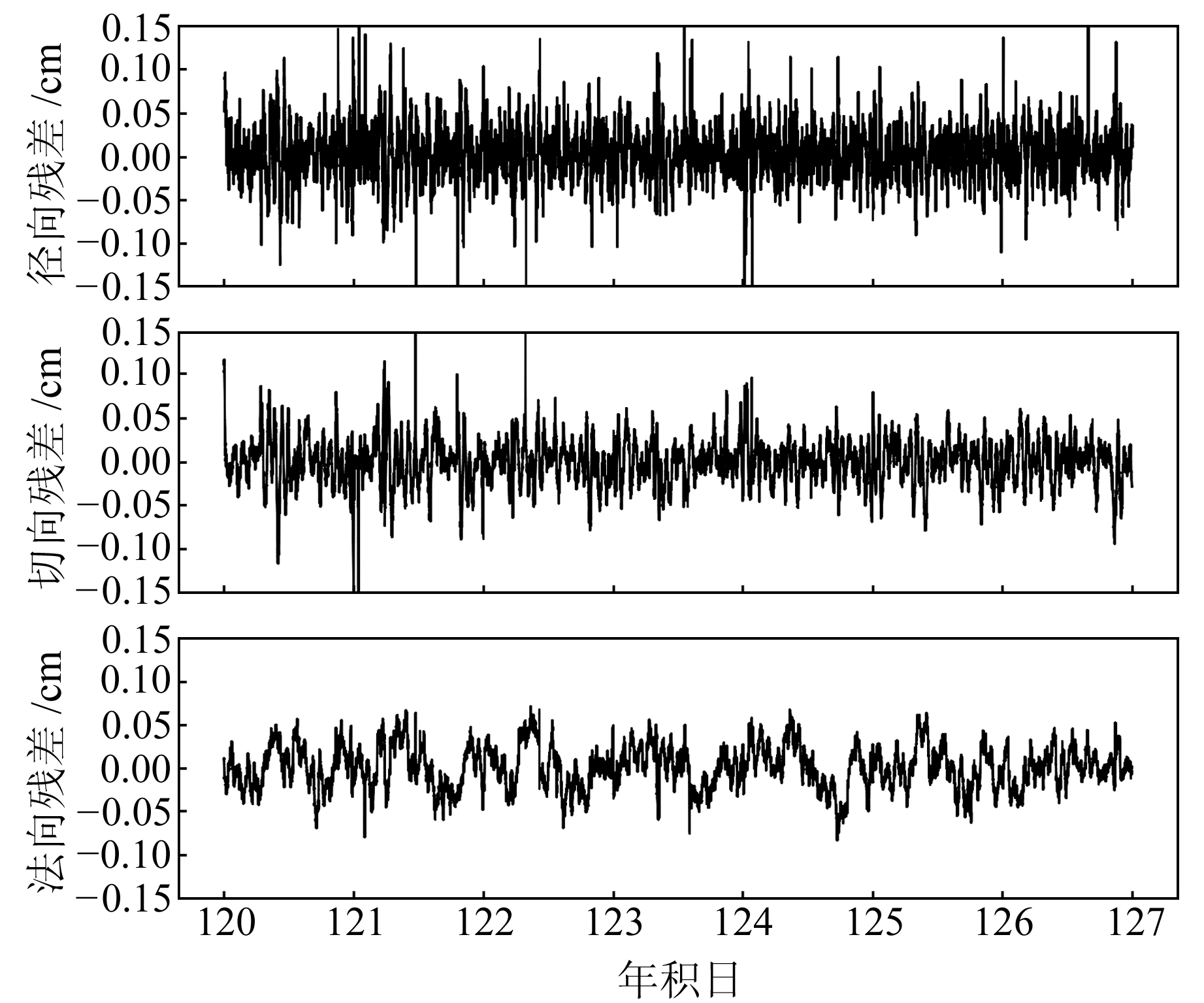
|
图 3 SWARM-B卫星年积日120~126的运动学轨道与ESA轨道差值 Fig. 3 The residuals between kinematic orbit and product released by ESA for SWARM-B during doy 120~126 |

|
图 4 SWARM-C卫星年积日120~126的运动学轨道与ESA轨道差值 Fig. 4 The residuals between kinematic orbit and product released by ESA for SWARM-C during doy 120~126 |
|
|
表 2 年积日120~126运动学轨道与真值轨道比较后的平均RMS Tab. 2 The mean RMS values of kinematic orbit and product released by ESA during doy 120~126 |
从图 2~4可以看出,SWARM卫星运动学轨道少量残差值在径向、切向和法向上存在较大差异。理论上,运动学定轨方法主要依赖于星载GPS接收机观测值的数量和质量,所以在定轨的过程中有些历元存在一些粗差或者缺失值的情况。从图中可以发现,SWARM卫星运动学轨道在法向上的残差序列波动范围明显比径向和切向波动范围小,定轨精度略高。根据平均RMS结果(表 2)可知,SWARM-A卫星径向、切向和法向平均RMS分别为2.68 cm、2.58 cm、2.43 cm; SWARM-B卫星径向、切向和法向平均RMS分别为2.96 cm、2.68 cm、2.43 cm; SWARM-C卫星径向、切向和法向平均RMS分别为2.69 cm、2.52 cm、2.28 cm。SWARM卫星3个方向的平均RMS均小于3 cm,运动学精密定轨精度达到cm级。
2.4 简化动力学轨道外符合精度评定将解算的SWARM卫星简化动力学轨道与ESA发布的科学轨道进行对比,在RTN坐标系下进行分析,结果如图 5~7和表 3所示。
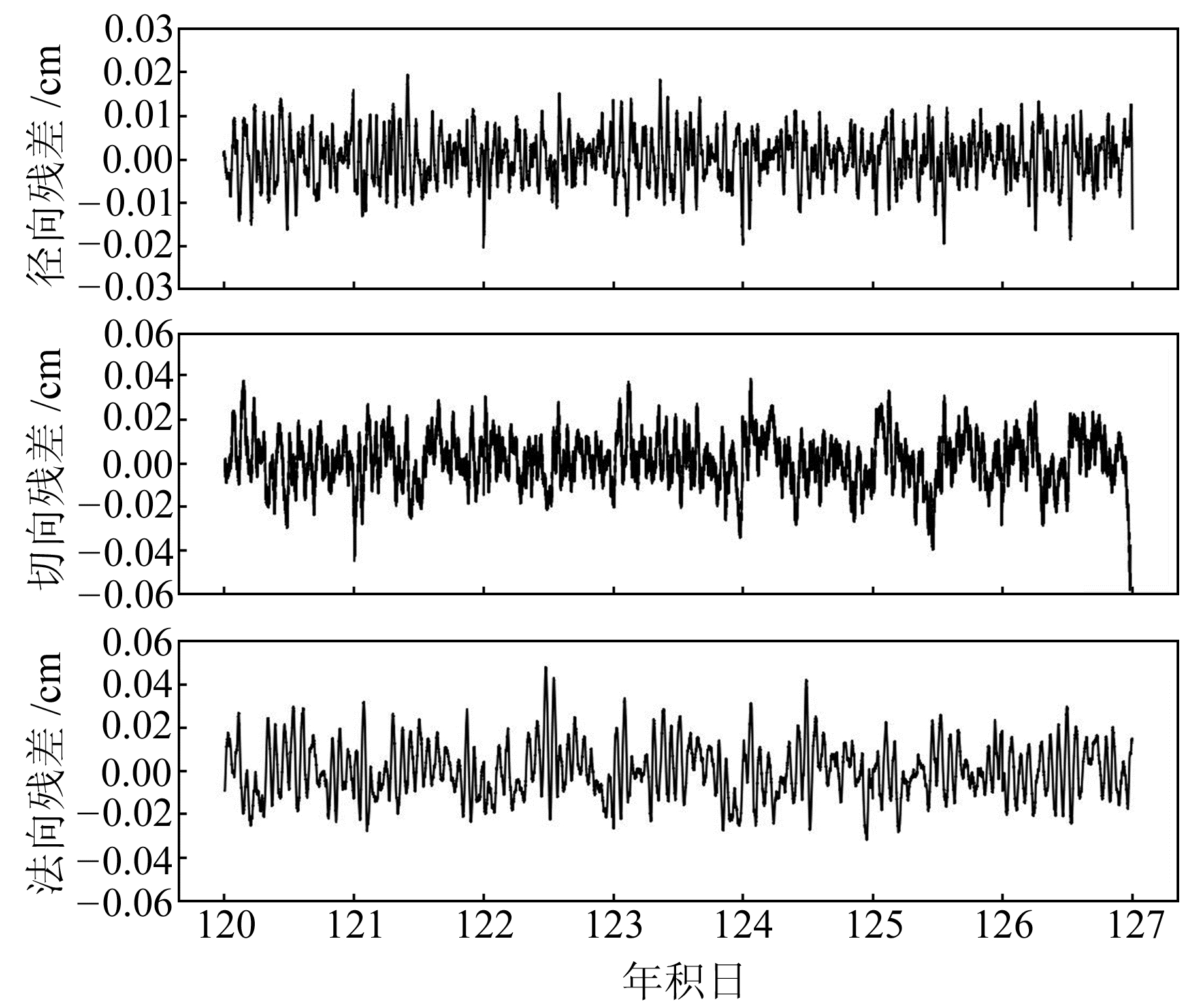
|
图 5 SWARM-A卫星年积日120~126的简化动力学轨道与ESA轨道差值 Fig. 5 The residuals between reduced-dynamic orbit and product released by ESA for SWARM-A during doy 120~126 |
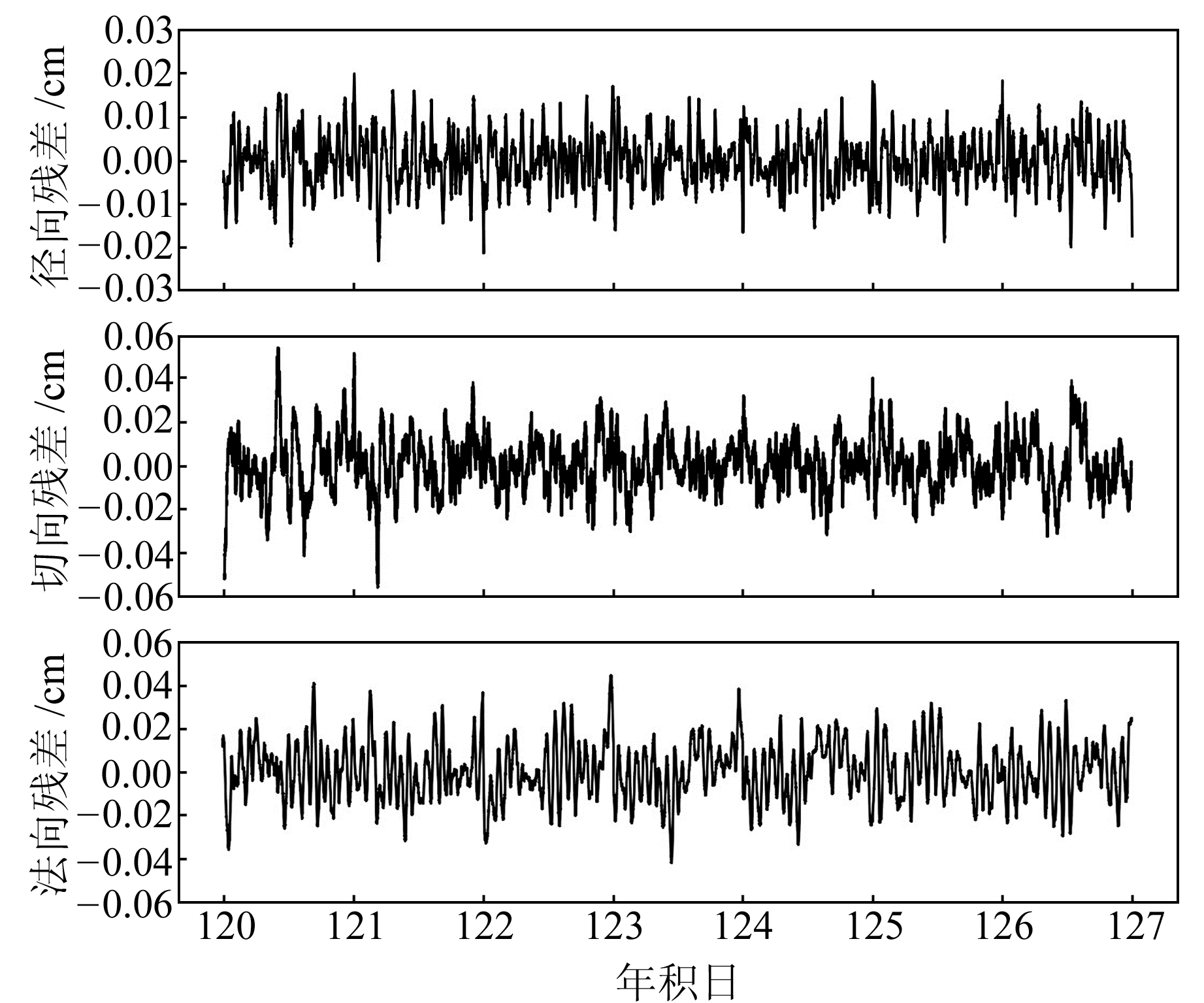
|
图 6 SWARM-B卫星年积日120~126的简化动力学轨道与ESA轨道差值 Fig. 6 The residuals between reduced-dynamic orbit and product released by ESA for SWARM-B during doy 120~126 |
|
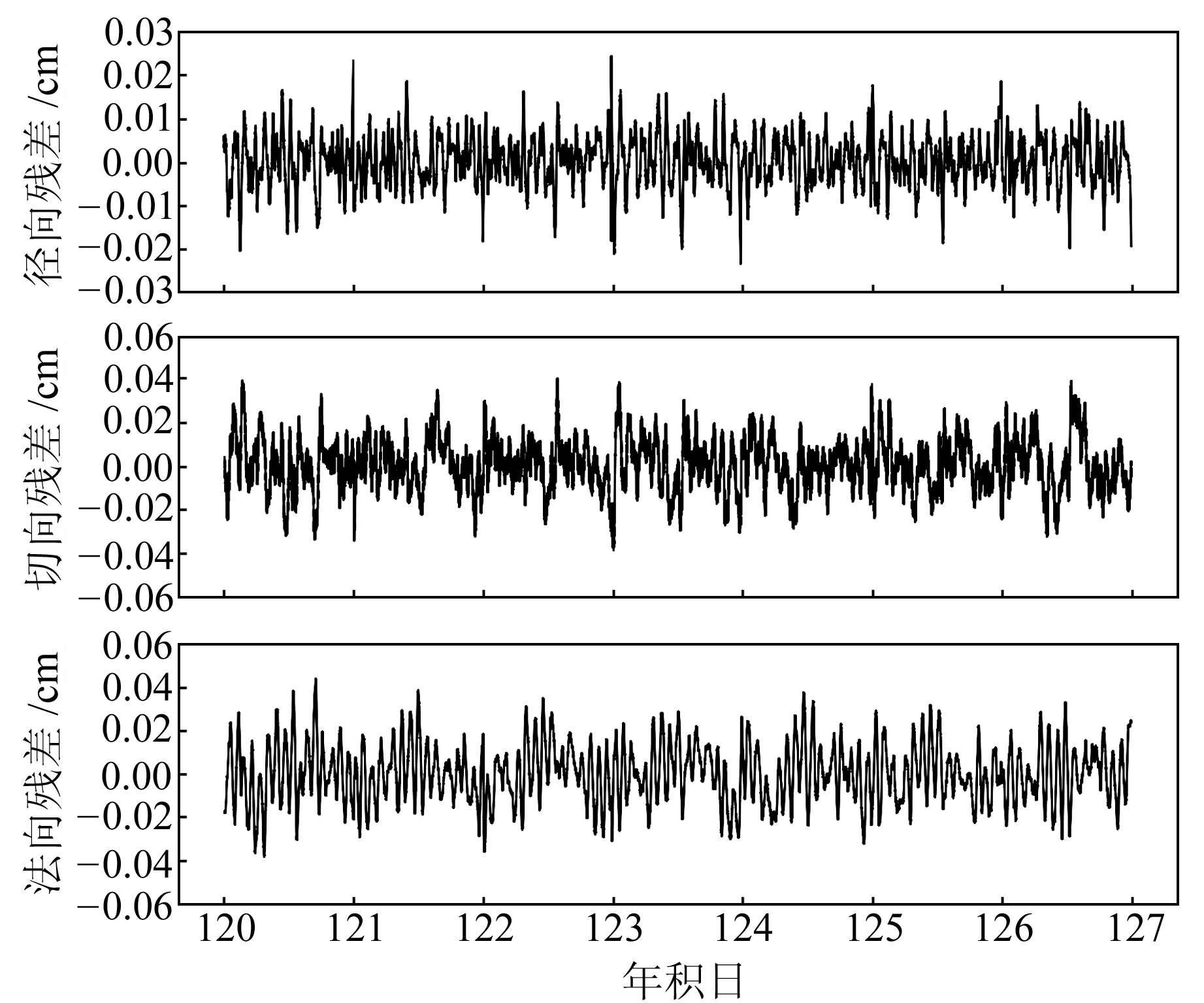
图 7 SWARM-C卫星年积日120-126的简化动力学轨道与ESA轨道差值 Fig. 7 The residuals between reduced-dynamic orbit and product released by ESA for SWARM-C during doy 120-126 |
|
|
表 3 年积日120-126简化动力学轨道与真值轨道比较后的平均RMS Tab. 3 The mean RMS values of reduced-dynamic orbit and product released by ESA during doy 120~126 |
从图 5~7可以看出,SWARM卫星轨道残差在每天的00:00和24:00有较大的波动,这是因为简化动力学定轨时,弧段两端的约束比较弱,存在一定的边界效应。从精密星历的时间间隔也可以发现,23:45后的星历只能通过外推获取,这必定会对轨道精度造成一定影响[16]。另外,简化动力学轨道残差序列图在切向和法向上存在微弱的周期性误差,从图中可以看出,在1 d的弧段中,切向残差会出现2次波峰和波谷,而法向残差值则是在中午至下午14:00时间段内达到最大。轨道切向是因为伪随机脉冲和逐段常量经验加速度未能完全吸收大气阻力模型等误差,导致残差序列产生周期性变化;法向是因为太阳辐射光压误差和地球反照光压误差导致残差序列产生周期性变化[17]。从表 3可以看出,SWARM-A卫星径向、切向和法向平均RMS分别为0.63 cm、1.19 cm、1.24 cm; SWARM-B卫星径向、切向和法向平均RMS分别为0.63 cm、1.27 cm、1.33 cm; SWARM-C卫星径向、切向和法向平均RMS分别为0.65 cm、1.23 cm、1.38 cm, 定轨精度高于文献[14]和文献[17]给出的SWARM卫星简化动力学定轨结果,且3颗卫星的3D-RMS平均值均小于2 cm,精度高于运动学精密定轨结果。
2.5 运动学轨道与简化动力学轨道对比分析本文将解算后的运动学轨道与简化动力学轨道进行作差,将残差序列在RTN坐标系中列出,计算SWARM卫星R、T、N 3个方向的平均RMS,结果如图 8和表 4所示。
|
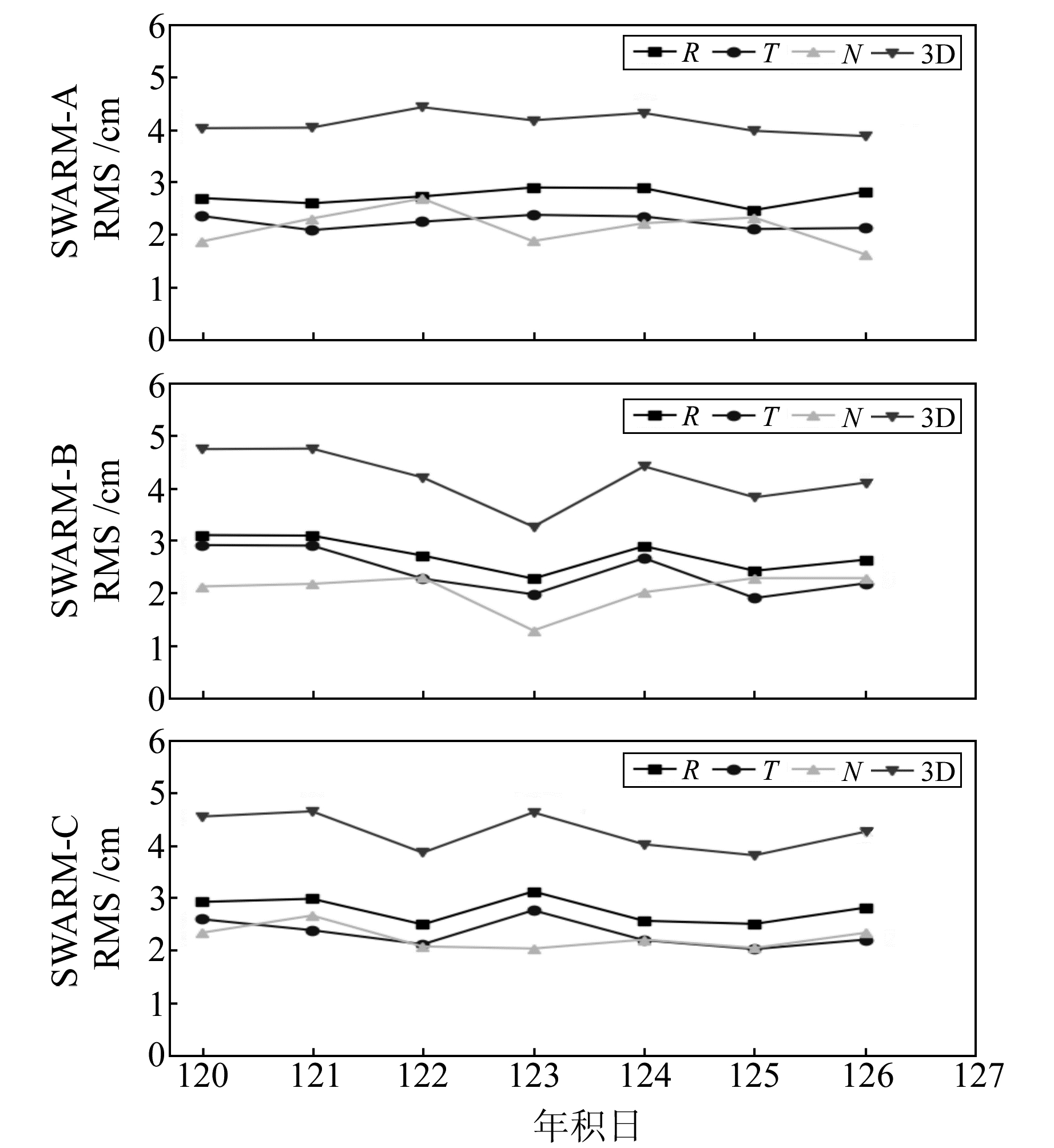
图 8 SWARM卫星运动学轨道和简化动力学轨道比较后的RMS Fig. 8 The RMS values between kinematic orbit and reduced-dynamic orbit for SWARM |
|
|
表 4 SWARM卫星运动学轨道和简化动力学轨道比较后的平均RMS Tab. 4 The mean RMS values between kinematic orbit andreduced-dynamic orbit for SWARM |
从图 8可以看出,将SWARM卫星解算得到的运动学轨道和简化动力学轨道作差,得到R、T、N 3个方向的RMS在很小的范围内变化,定轨结果比较稳定。从表 4可以看出,平均RMS和运动学轨道外符合精度评估得到的平均RMS较为接近,一方面可以说明随着科研技术和设备的发展,运动学方法的定轨精度在不断提高,与简化动力学轨道精度的差距逐步缩小,精度同样达到cm级;另一方面也证明了简化动力学定轨方法的优越性,其定轨精度非常接近ESA发布的精密科学轨道。
2.6 不同星历下SWARM卫星定轨精度比较目前国际GNSS服务组织(IGS)发布的星历主要有3种,分别为精密、快速和超快速星历,其中,超快速星历是IGS为满足用户对于GPS卫星的近实时应用,于2000年发布的一款产品[10]。表 5是IGS官网(http://www.igs.org/products)提供的不同星历精度信息。
|
|
表 5 不同星历精度信息 Tab. 5 Precision information of different ephemeris |
为比较不同GPS卫星星历对SWARM卫星定轨的影响,采用以下3种方案:1)选择CODE中心提供的15 min间隔的精密星历和30 s采样间隔的精密钟差;2)选择IGS提供的快速星历和5 min采样间隔的钟差;3)选择IGS提供的超快速星历。以2017-05-01(年积日121)SWARM卫星星载GPS观测数据为例进行定轨研究,将定轨结果与ESA发布的精密科学轨道进行对比,结果如图 9、10和表 6、7所示。
|
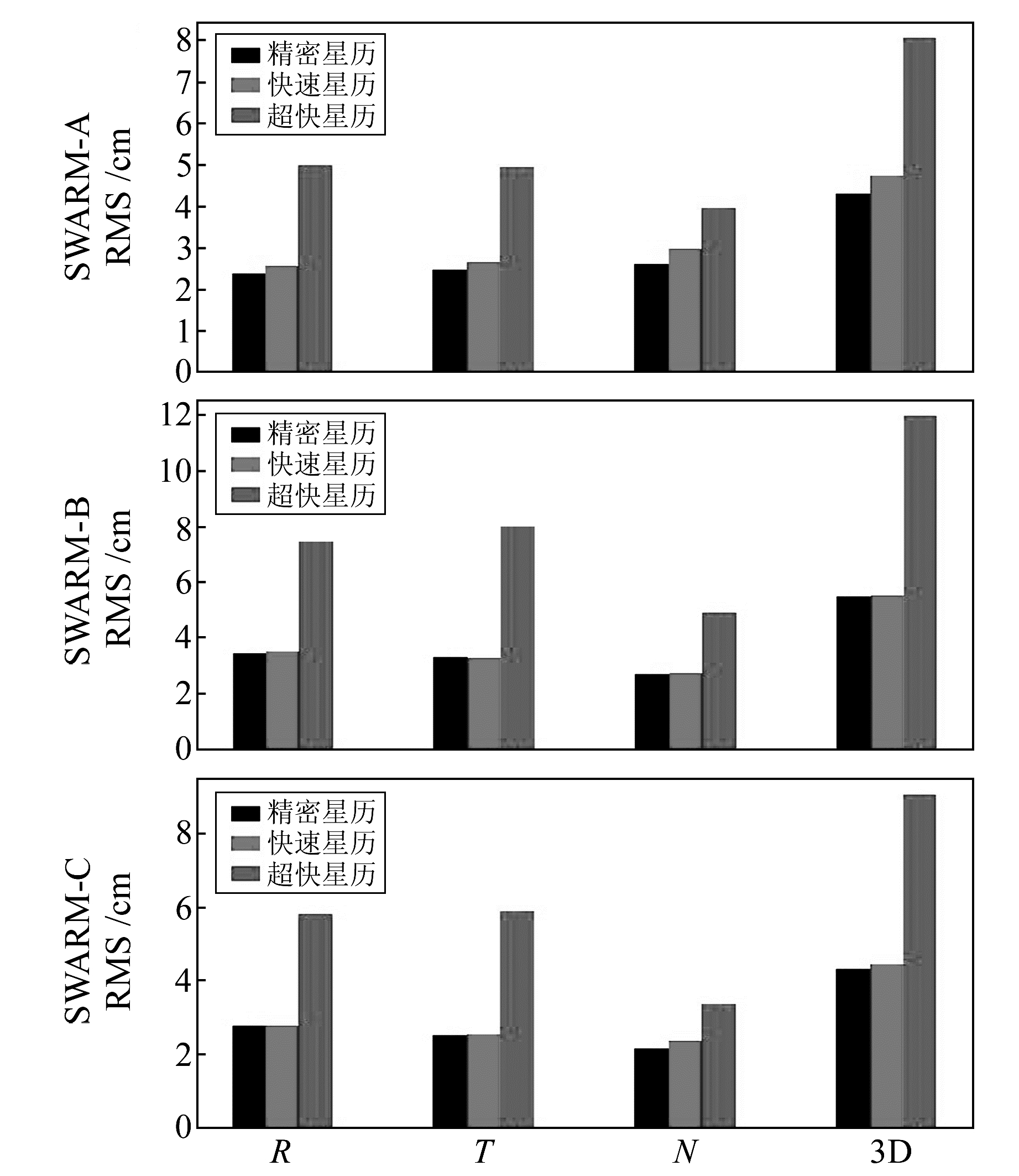
图 9 不同星历下运动学轨道对比分析 Fig. 9 Kinematic orbit analysis of different ephemeris |
|
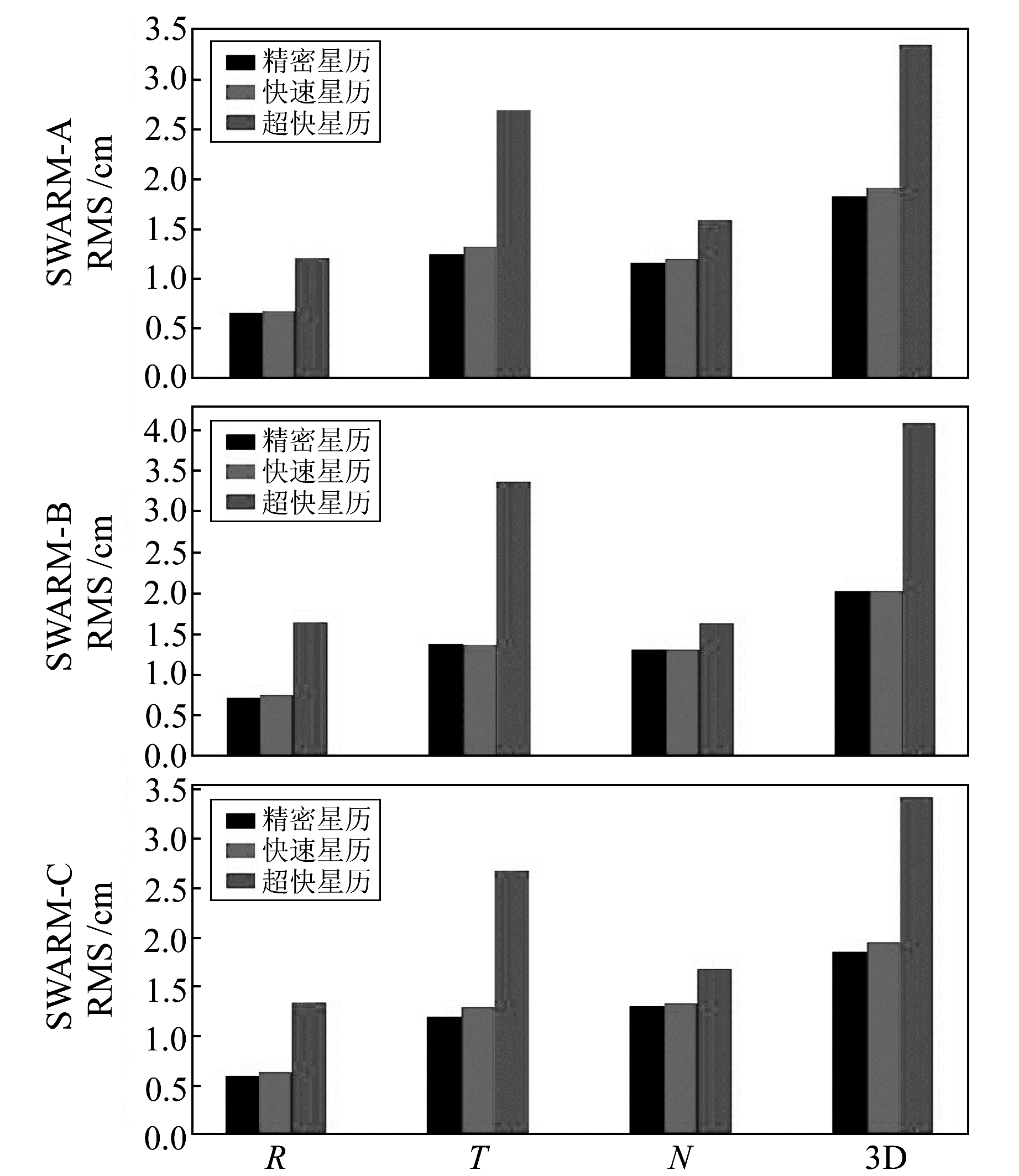
图 10 不同星历下简化动力学轨道对比分析 Fig. 10 Reduced-dynamic orbit analysis of different ephemeris |
|
|
表 6 不同星历下SWARM卫星运动学轨道平均RMS Tab. 6 The mean RMS values of SWARM kinematic orbit during different ephemeris |
|
|
表 7 不同星历下SWARM卫星简化动力学轨道平均RMS Tab. 7 The mean RMS values of SWARM reduced-dynamic orbit during different ephemeris |
从图 9和10可以看出,在CODE精密星历和IGS快速星历下,运动学轨道和简化动力学轨道与事后科学轨道对比分析后的差值变化不明显,RMS只在mm级范围内波动。当使用IGS超快速星历时,RMS明显增大,径向和切向RMS基本上是精密轨道和快速轨道RMS的2倍。表 6和7则显示,运动学近实时轨道径向平均RMS为6.08 cm,切向和法向RMS分别为6.27 cm和4.16 cm;简化动力学近实时轨道径向平均RMS为1.39 cm,切向和法向分别为2.90 cm和1.63 cm。综上可知,使用IGS快速星历对SWARM卫星进行定轨的精度与ESA发布的精密定轨精度基本一致,而在SWARM卫星近实时定轨研究中,使用IGS超快速星历确定的轨道误差符合表 5所示信息,精度低于IGS快速星历的定轨结果。
3 结语对于SWARM卫星而言,选择不同的定轨方法,其轨道精度会有较明显的差异。本文通过对SWARM 3颗卫星2017-04-30~05-06共7 d星载GPS观测数据进行定轨分析,并在不同GPS卫星星历下进行定轨研究,得到以下结论:
1) SWARM卫星运动学轨道会出现少量残差值异常现象,这是因为运动学定轨完全使用观测值信息,过分依赖观测值质量,导致少量历元定轨精度较差。SWARM卫星3个方向的平均RMS均小于3 cm,轨道精度达到cm级。
2) SWARM卫星轨道切向残差序列的周期性变化,是由伪随机脉冲和逐段常量经验加速度未能完全吸收的大气阻力模型等误差产生的;法向残差序列的周期性变化,是由太阳辐射光压误差和地球反照光压误差产生的。简化动力学轨道残差在各天的弧段两端存在一定的边界效应,出现数值较大的情况。SWARM卫星轨道径向平均RMS在0.65 cm左右,切向和法向在1.3 cm左右,轨道精度高于预期1~2 cm的要求。
3) 通过对运动学轨道和简化动力学轨道进行对比分析,一方面直接验证了随着星载GPS技术的发展,运动学定轨精度已经达到cm级;另一方面间接证明了简化动力学定轨方法的优越性,其精度与ESA发布的精密科学轨道精度非常接近。
4) 使用精密星历、快速星历和超快速星历对SWARM卫星进行定轨,结果表明,使用IGS快速星历进行定轨的精度与ESA发布的精密定轨精度近似相等,而在SWARM卫星近实时定轨研究中,使用IGS超快速星历确定的运动学轨道3D-RMS为9.68 cm,简化动力学轨道3D-RMS为3.61 cm,低于IGS快速星历的定轨精度。
| [1] |
付郁, 云成. ESA首个磁场监测卫星星座"蜂群"[J]. 卫星应用, 2014(3): 73 (Fu Yu, Yun Cheng. ESA's First Monitoring Satellite Constellation "Swarm"[J]. Satellite Application, 2014(3): 73)
(  0) 0) |
| [2] |
宁津生, 王正涛, 超能芳. 国际新一代卫星重力探测计划研究现状与进展[J]. 武汉大学学报:信息科学版, 2016, 41(1): 1-8 (Ning Jinsheng, Wang Zhengtao, Chao Nengfang. Research Status and Progress in International Next-Generation Satellite Gravity Measurement Missions[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 1-8)
(  0) 0) |
| [3] |
陈秋杰, 沈云中, 张兴福, 等. 基于GRACE卫星数据的高精度全球静态重力场模型[J]. 测绘学报, 2016, 45(4): 396-403 (Chen Qiujie, Shen Yunzhong, Zhang Xingfu, et al. GRACE Data-Based High Accuracy Global Static Earth's Gravity Field Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 396-403)
(  0) 0) |
| [4] |
Zheng W, Xu H Z. Progress in Satellite Gravity Recovery from Implemented CHAMP, GRACE and GOCE and Future GRACE Follow-on Missions[J]. Geodesy and Geodynamics, 2015, 6(4): 241-247 DOI:10.1016/j.geog.2015.05.005
(  0) 0) |
| [5] |
Jäggi A, Dahle C, Arnold D, et al. SWARM Kinematic Orbits and Gravity Fields from 18 Months of GPS Data[J]. Advances in Space Research, 2016, 57(1): 218-233 DOI:10.1016/j.asr.2015.10.035
(  0) 0) |
| [6] |
李建成, 张守建, 邹贤才, 等. GRACE卫星非差运动学厘米级定轨[J]. 科学通报, 2009, 54(16): 2355-2362 (Li Jiancheng, Zhang Shoujian, Zou Xiancai, et al. Zero-Difference Kinematic POD of GRACE with Precision of Centimeters[J]. Chinese Science Bulletin, 2009, 54(16): 2355-2362)
(  0) 0) |
| [7] |
Jäggi A, Hugentobler U, Beutler G. Pseudo-Stochastic Orbit Modling Techniques for Low-Earth Orbiters[J]. Journal of Geodesy, 2006, 80(1): 47-60 DOI:10.1007/s00190-006-0029-9
(  0) 0) |
| [8] |
Yunck T P, Wu S C, Wu J T, et al. Precise Tracking of Remote Sensing Satellites with the Global Positioning System[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(1): 108-116 DOI:10.1109/36.45753
(  0) 0) |
| [9] |
吴琼宝, 赵春梅, 田华. 不同星历下低轨卫星轨道精度分析[J]. 导航定位学报, 2017, 5(4): 21-24 (Wu Qiongbao, Zhao Chunmei, Tian Hua. Accuracy Analysis of LEO Satellite Orbit Determination Based on Different Ephemeris[J]. Journal of Navigation and Positioning, 2017, 5(4): 21-24)
(  0) 0) |
| [10] |
秦显平.星载GPS低轨卫星定轨理论及方法研究[D].郑州: 信息工程大学, 2009 (Qin Xianping. Research on Precision Orbit Determination Theory and Method of Low Earth Orbiter Based on GPS Technique[D]. Zhengzhou: Information Engineering University, 2009) http://www.cqvip.com/QK/93330B/201001/34257860.html
(  0) 0) |
| [11] |
郭金运, 宗干, 李旺, 等. GPS单星单历元模糊度与电离层延迟分类解算[J]. 山东科技大学学报:自然科学版, 2015, 34(1): 54-60 (Guo Jinyun, Zong Gan, Li Wang, et al. Classification Solution of Single-Epoch Ambiguity and Ionospheric Delay for Single GPS Satellite[J]. Journal of Shandong University of Science and Technology, 2015, 34(1): 54-60)
(  0) 0) |
| [12] |
胡志刚, 赵齐乐, 郭靖, 等. GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(1): 34-38 (Hu Zhigang, Zhao Qile, Guo Jing, et al. Research on Impact of GPS Phase Center Variation on Precise Orbit Determination of Low Earth Orbit Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 34-38)
(  0) 0) |
| [13] |
秦建, 郭金运, 孔巧丽, 等. Jason-2卫星星载GPS数据cm级精密定轨[J]. 武汉大学学报:信息科学版, 2014, 39(2): 137-141 (Qin Jian, Guo Jinyun, Kong Qiaoli, et al. Precise Orbit Determination of Jason-2 with Precision of Centimeters Based on Satellite-Borne GPS Technique[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 137-141)
(  0) 0) |
| [14] |
张兵兵, 聂琳娟, 吴汤婷, 等. SWARM卫星简化动力学厘米级精密定轨[J]. 测绘学报, 2016, 45(11): 1278-1284 (Zhang Bingbing, Nie Linjuan, Wu Tangting, et al. Centimeter Precise Orbit Determination for Swarm Satellite via Reduced-Dynamic Method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1278-1284 DOI:10.11947/j.AGCS.2016.20160284)
(  0) 0) |
| [15] |
Zhang B B, Wang Z T, Zhou L, et al. Precise Orbit Solution for SWARM Using Space-Borne GPS Data and Optimized Pseudo-Stochastic Pulses[J]. Sensors, 2017, 17(3): 635-650 DOI:10.3390/s17030635
(  0) 0) |
| [16] |
张德成, 郑作亚, 刘娴, 等. 基于星载GPS数据的GRACE卫星动力法定轨[J]. 全球定位系统, 2013, 38(5): 1-4 (Zhang Decheng, Zheng Zuoya, Liu Xian, et al. GPS-Based Dynamic Orbit Determination of GRACE Satellite[J]. GNSS World of China, 2013, 38(5): 1-4 DOI:10.3969/j.issn.1008-9268.2013.05.001)
(  0) 0) |
| [17] |
田英国, 郝金明, 谢建涛, 等. SWARM卫星星载GPS精密定轨方法及精度分析[J]. 测绘科学技术学报, 2016, 33(5): 452-457 (Tian Yingguo, Hao Jinming, Xie Jiantao, et al. Swarm Precise Orbit Determination and Accuracy Analysis Using on Board GPS Data[J]. Journal of Geomatics Science and Technology, 2016, 33(5): 452-457)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


