随着卫星导航系统的快速发展,星载GNSS精密定轨技术取得长足的进步。自1992年T/P卫星利用星载GPS技术获取cm级轨道以来,越来越多的低轨卫星通过搭载星载GPS接收机,获取了cm级精度的轨道[1-6]。卫星定轨精度受数据质量、摄动力建模、数据处理策略等技术因素影响。GNSS卫星主要考虑太阳光压摄动模型[7],低轨卫星常采用经验力模型或伪随机脉冲模型。Beutler等[8]提出采用伪随机脉冲方法进行低轨卫星定轨,并给出提高执行效率的消元回代算法;Guo等[9]通过不同的重力场模型拟合CHAMP和GRACE卫星轨道,使用经验力和伪随机脉冲模型吸收力学模型误差,得到较好的拟合轨道;韩保民等[10]分析伪随机脉冲在不同情形下的大小变化及其对定轨精度的调节作用,在力学模型误差较大的情况下,随机脉冲的设置能有效补偿和吸收模型误差,从而提高定轨精度;赵春梅等[11]、刘伟平等[12]及田英国等[13]将伪随机脉冲及经验力模型联合用于低轨卫星GRACE、CHAMP及SWARM,吸收难以精确模型化的摄动力,获得了cm级的定轨精度。
本文通过设置不同周期的伪随机脉冲及其与ECOM光压模型组合,分析伪随机脉冲吸收GRACE卫星及GNSS卫星未模型化摄动力的有效性,研究其在卫星轨道拟合中的应用和效果。
1 卫星轨道拟合基本原理 1.1 卫星轨道拟合原理设任意t时刻,卫星在惯性系下的位置和速度分别为r和v,构成该时刻的状态量X作为轨道拟合时的虚拟观测量。同时设t0为初始时刻,初始时刻卫星的位置r0和速度v0构成初轨X0。根据卫星摄动理论,设卫星在任意t时刻的状态量近似值为X,状态量X对初始时刻状态量X0的偏导数定义为状态转移矩阵Φ(t),对卫星所受力学参数p的偏导数为敏感矩阵S(t),即
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( t \right) = \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial \mathit{\boldsymbol{X}}_0^{\rm{T}}}} $ | (1) |
| $ \mathit{\boldsymbol{S}}\left( t \right) = \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial {\mathit{\boldsymbol{p}}^{\rm{T}}}}} $ | (2) |
对状态量X进行泰勒展开,得到:
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{\bar X}} + \frac{{\partial \mathit{\boldsymbol{\bar X}}}}{{\partial \mathit{\boldsymbol{X}}_0^{\rm{T}}}}\delta {\mathit{\boldsymbol{X}}_0} + \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial {\mathit{\boldsymbol{p}}^{\rm{T}}}}}\delta \mathit{\boldsymbol{p}} + \mathop \sum \limits_{i = 1}^n \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial \mathit{\boldsymbol{q}}_{{t_i}}^{\rm{T}}}}\delta {\mathit{\boldsymbol{q}}_{{t_i}}} $ | (3) |
其中, 初轨参数X0、力学参数p及伪随机脉冲参数qt1、qt2…qtn(t1 < t2 < … < tn < t)是待估参数,状态量X及初轨、力学参数和伪随机脉冲偏导数可通过轨道积分得到,详细参考文献[14]。
1.2 伪随机脉冲基本模型伪随机脉冲(pseudo-stochastic-pulses)是指在给定的历元时刻对卫星速度施加一个脉冲或一个微小增量,但卫星的位置在该时刻保持不变。该时刻的速度增量作为一个待估参数,用于吸收未模型化的摄动力对卫星轨道的影响,在定轨中和其他参数一并解算。由伪随机脉冲的定义可知,伪随机脉冲只改变该历元时刻卫星的速度,不改变其位置。因此,在历元时刻有:
| $ {\mathit{\boldsymbol{r}}_{{t_i}}} = r_{{t_i}}^ + = \mathit{\boldsymbol{r}}_{{t_i}}^ - $ | (4) |
| $ {\mathit{\boldsymbol{v}}_{{t_i}}} = \mathit{\boldsymbol{v}}_{{t_i}}^ + = \mathit{\boldsymbol{v}}_{{t_i}}^ - + {\mathit{\boldsymbol{M}}_{{t_i}}}{\mathit{\boldsymbol{q}}_{{t_i}}} $ | (5) |
式(4)和式(5)中,“-”为施加伪随机脉冲前,“+”为施加伪随机脉冲后,Mti为ti时刻伪随机脉冲qti所在坐标系与卫星位置速度所在坐标系之间的旋转矩阵。结合式(3),状态量对伪随机脉冲偏导数为:
| $ \frac{{\partial \mathit{\boldsymbol{\bar X}}}}{{\partial \mathit{\boldsymbol{q}}_{{t_i}}^{\rm{T}}}} = \left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{0}}\\ {{\mathit{\boldsymbol{M}}_{{t_i}}}} \end{array}} \right) $ | (6) |
分别选取GRACE低轨卫星精密星历数据和GPS、GLONASS、Galileo及BDS等4个卫星导航系统的精密星历数据进行轨道拟合实验。GRACE卫星选取德国地学中心GFZ发布的2010-01-11~01-15共5 d的GRACE-A卫星精密星历,采样间隔为10 s;GNSS卫星星历采用德国地学中心GFZ发布的2015-01-05多系统精密星历数据。通过轨道拟合方法,利用伪随机脉冲吸收未模型化的摄动力,检验拟合后的轨道与精密轨道之间的差异,对拟合轨道进行精度评价。数据实验在卫星精密定轨定位与重力场恢复系统(satellite precise orbit determination and gravity recovery system, SPODAGRS)上进行。该软件是本文第一作者在参考GPSTK等现有GNSS数据处理软件基础上,采用标准C++语言独立开发的一套卫星精密定轨定位与重力场恢复软件系统。力学模型统一采用IERS2010推荐模型,重力场模型采用EGM2008模型,GRACE卫星采用150阶次,GNSS卫星采用10阶次,积分器采用配置积分器。GRACE卫星积分步长1 min,GNSS卫星积分步长60 min,均为10阶。GNSS卫星太阳光压模型采用ECOM九参数模型,在D、Y、B 3个方向施加伪随机脉冲,GRACE卫星在R、T、N 3个方向施加伪随机脉冲。
3 低轨卫星轨道拟合精度分析选取GFZ发布的2010-01-11~01-15 GRACE-A卫星精密星历数据,按照上述轨道拟合策略,伪随机脉冲分别每隔10 min、15 min和30 min设置1次,共进行3组实验,结果如表 1~3所示。
|
|
表 1 R方向拟合轨道精度统计 Tab. 1 Orbit fitting precision in R direction |
|
|
表 2 T方向拟合轨道精度统计 Tab. 2 Orbit fitting precision in T direction |
|
|
表 3 N方向拟合轨道精度统计 Tab. 3 Orbit fitting precision in N direction |
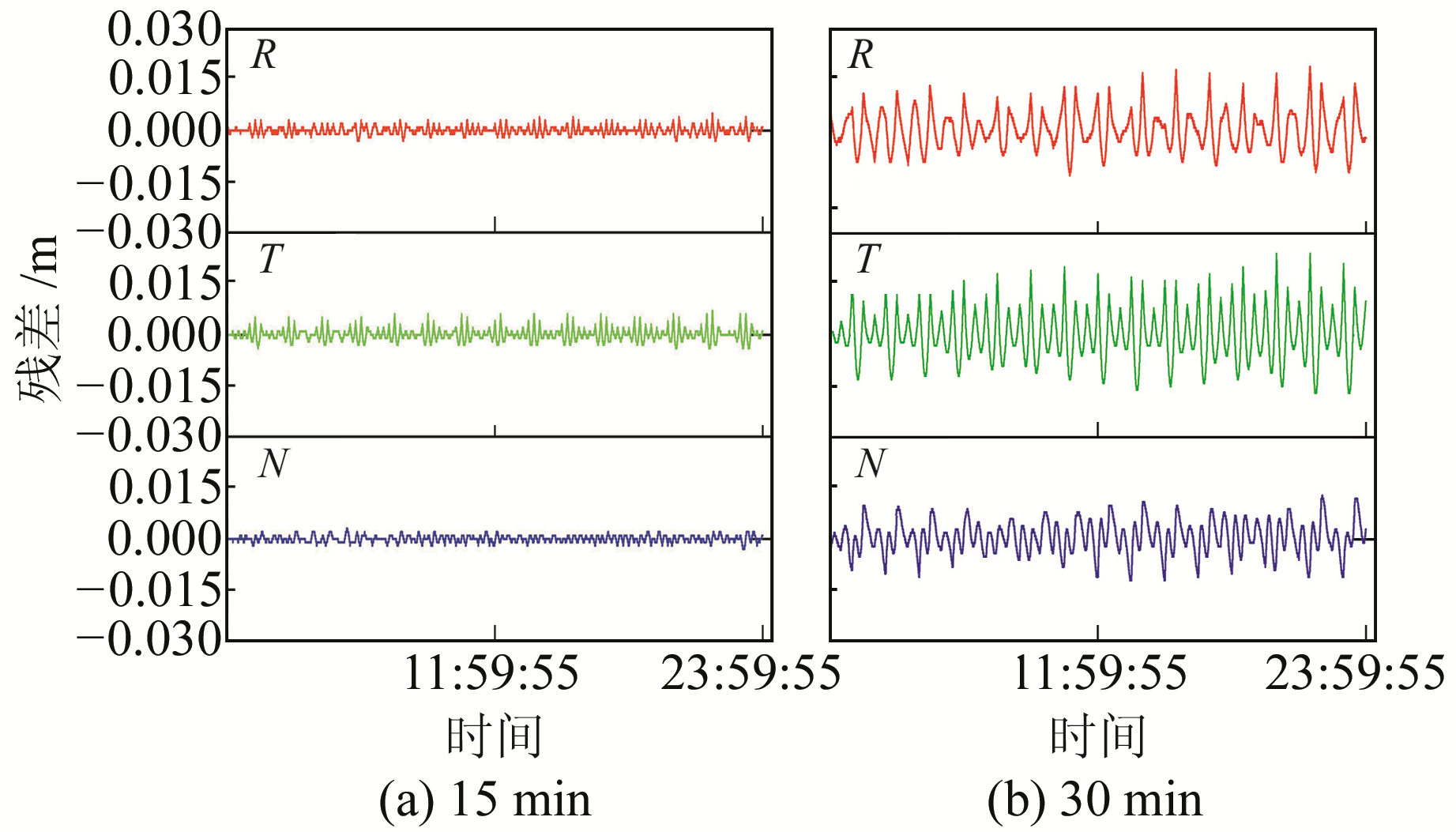
表 1~3统计了GRACE-A卫星在R、T、N方向的轨道拟合精度,图 1绘制了年积日11 d当天的拟合残差时间序列。由表 1~3可知,伪随机脉冲在吸收未模型化的摄动力方面效果非常显著,R、T、N方向RMS均在0.01 m以内。拟合过程中对地球引力进行建模,大气阻力、太阳光压等摄动力采用伪随机脉冲进行吸收,得到精度较高的拟合轨道。随着伪随机脉冲设置周期的增大,轨道拟合精度有所下降:当间隔10 min设置1组伪随机脉冲时,拟合后RMS不超过0.001 m,与精密轨道差值最大不超过0.003 m,拟合轨道与精密轨道几乎重合;当间隔15 min设置1组伪随机脉冲时,3个方向RMS均不超过0.002 m,最大不超过0.007 m;当间隔30 min设置1组伪随机脉冲时,3个方向RMS不超过0.008 m,与精密星历最大偏差不超过0.025 m,且T方向精度略低于R和N方向,这与GRACE-A未模型化的摄动力主要来自T方向大气阻力有关。随着伪随机脉冲设置周期的增加,伪随机脉冲次数逐渐减少,其吸收未模型化摄动力效应的能力逐渐减弱,拟合轨道RMS逐渐增大。从图 1的残差序列也可以明显看出,使用伪随机脉冲进行GRACE-A卫星轨道拟合时,R和N方向拟合结果优于T方向,而间隔15 min的伪随机脉冲拟合结果明显优于间隔30 min的结果。
|
图 1 年积日11 d拟合残差序列 Fig. 1 Fitting residual series for doy 11 |
鉴于GRACE-A卫星运行周期约为90 min,在进行轨道拟合时,1个周期内设置3~9次伪随机脉冲就能保证拟合轨道精度优于0.01 m。如果脉冲次数进一步增加,一方面会降低计算效率,另一方面拟合精度已经较高,再提高精度也没有实质意义。
4 GNSS卫星轨道拟合精度分析为分析伪随机脉冲对GPS、BDS、GLONASS和Galileo四大导航系统卫星轨道拟合精度的影响,进行以下2组实验:ECOM九参数光压模型+伪随机脉冲实验方案,简称方案1;纯伪随机脉冲实验方案,简称方案2。其他力学模型及积分器均不变。
方案1中,在采用ECOM九参数光压模型的基础上,按照不设置伪随机脉冲、每8 h设置1组伪随机脉冲、每12 h设置1组伪随机脉冲进行3个实验,结果见图 2和图 3。

|
图 2 方案1拟合轨道3D RMS比较(GPS+Galileo) Fig. 2 3D RMS of fitting orbit for scheme 1 (GPS+Galileo) |

|
图 3 方案1拟合轨道3D RMS比较(GLONASS+BDS) Fig. 3 3D RMS of fitting orbit for scheme 1 (GLONASS+BDS) |
由图 2和图 3可知,仅采用九参数ECOM太阳光压模型时,4大卫星导航系统共70颗卫星的拟合轨道精度均优于0.08 m,其中大部分卫星拟合精度优于0.01 m,少部分卫星拟合精度在0.02 m左右,只有G07、G11、E12、R14、R20、R21、R22、C04、C11、C12共10颗星RMS超过0.02 m,表明ECOM太阳光压模型在多个卫星导航系统中都是有效的,但并不是完全有效;每8 h设置1组伪随机脉冲时,拟合精度普遍比不使用伪随机脉冲时有所提高,尤其Galileo卫星E12,拟合精度由约0.04 m提高到约0.02 m,而BDS卫星C12拟合精度由0.06 m提高到约0.04 m,表明未模型化的摄动力能够被伪随机脉冲很好地吸收,从而提高了拟合精度;当每12 h设置1组伪随机脉冲,也就是在每天午时施加1组伪随机脉冲以吸收ECOM模型未模型化的摄动力时,大部分卫星拟合精度有明显提高,尤其是与不使用伪随机脉冲时精度较差的卫星相比,如G07、G11、G16、E12、R14、R20、C11、C12卫星,精度均优于0.01 m,表明ECOM模型与伪随机脉冲组合使用能够提高拟合轨道的精度,且在ECOM太阳光压模型建模前提下,伪随机脉冲不宜设置过多,每天只在午时设置1组即可。
方案2中不使用太阳光压模型,与GRACE-A低轨卫星实验类似,完全使用伪随机脉冲进行轨道拟合实验,探讨伪随机脉冲在吸收太阳光压摄动力方面的能力。伪随机脉冲分别每隔45 min、120 min和240 min设置1组,实验结果如图 4和图 5所示。

|
图 4 方案2拟合轨道3D RMS比较(GPS+Galileo) Fig. 4 3D RMS of fitting orbit for scheme 2 (GPS+Galileo) |

|
图 5 方案2拟合轨道3D RMS比较(GLONASS+BDS) Fig. 5 3D RMS of fitting orbit for scheme 2 (GLONASS+BDS) |
由图 4和图 5可知,在完全使用伪随机脉冲的前提下,设置周期越短,伪随机脉冲次数越多,拟合精度越高,且不论是何种导航系统卫星,伪随机脉冲均能够有效吸收未模型化的摄动力。当每隔240 min设置1组伪随机脉冲时,GPS和Galileo卫星拟合精度约为0.9 m,GLONASS卫星拟合精度约为1.3 m,BDS卫星拟合精度约为1.1 m;当每隔120 min设置1组伪随机脉冲时,GPS和Galileo卫星拟合精度提高至约0.2 m,GLONASS卫星拟合精度提高至约0.3 m,BDS卫星拟合精度提高至约0.2 m;当每隔45 min设置1组伪随机脉冲时,所有GNSS卫星拟合精度均优于0.05 m,进一步表明伪随机脉冲在吸收太阳光压方面具有普遍性,无论何种导航系统均适用。由于上述实验采用的GNSS卫星精密星历采样间隔为15 min,伪随机脉冲设置到45 min基本已达极限,如果缩短至30 min以内,会出现伪随机脉冲个数比虚拟观测量个数还多的情况,从而导致解算时法矩阵秩亏。
5 结语通过GRACE-A低轨卫星和4大导航系统卫星精密轨道的拟合实验,分析伪随机脉冲吸收大气阻力、太阳光压等摄动力对轨道拟合精度的影响效果,得出以下结论:
1) 伪随机脉冲在吸收未建模摄动力方面具有良好的效果,低轨卫星轨道拟合中能很好地吸收大气阻力,拟合精度达mm级;GNSS卫星轨道拟合中能很好地吸收太阳光压摄动力,拟合精度达到cm级。
2) 使用伪随机脉冲吸收低轨卫星大气阻力和GNSS卫星太阳光压摄动时,设置周期越短,吸收效果越好,拟合精度越高,反之拟合精度越低。但伪随机脉冲次数越多,解算待估参数越多,解算效率会明显降低。
3) 尽管伪随机脉冲能够有效吸收GNSS卫星太阳光压摄动影响,但进一步提高轨道拟合精度需要与ECOM太阳光压模型组合使用,每天设置1组伪随机脉冲即可保证拟合精度达到mm级,次数设置过多,拟合精度反而会下降。
4) 使用伪随机脉冲吸收低轨卫星和GNSS卫星未模型化的摄动力,本质上是以牺牲卫星速度的连续性为代价,而GNSS精密星历通常应用在地面精密定位等场合,一般不需要卫星的速度,只要能保证卫星轨道的高精度,卫星速度是否连续不影响地面用户的使用。
5) 在设置GRACE卫星伪随机脉冲间隔时直接使用了10 min、15 min和30 min固定间隔,主要考虑到GRACE卫星运行周期约为90 min,伪随机脉冲设置间隔不能超过其周期,同时也是一种经验做法,但脉冲时间间隔与拟合精度之间的理论推导及定量关系还有待进一步研究及完善。
| [1] |
张睿, 杨元喜. BDS/GPS联合定轨的贡献分析[J]. 武汉大学学报:信息科学版, 2017, 42(5): 600-608 (Zhang Rui, Yang Yuanxi. Contribution Analysis of BDS/GPS Combined Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 600-608)
(  0) 0) |
| [2] |
匡翠林.利用GPS非差数据精密确定低轨卫星轨道的理论及方法研究[D].武汉: 武汉大学, 2008 (Kuang Cuilin. Research on Precise Orbit Determination Theory and Methods of Lower Earth Orbit Satellites Using Zero-Difference GPS Data[D]. Wuhan: Wuhan University, 2008)
(  0) 0) |
| [3] |
Montenbruck O, Gill E, Kroes R. Rapid Orbit Determination of LEO Satellites Using IGS Clock and Ephemeris Products[J]. GPS Solutions, 2005, 9(3): 226-235 DOI:10.1007/s10291-005-0131-0
(  0) 0) |
| [4] |
Schrama E J O, Visser P N A M. Accuracy Assessment of the Monthly GRACE Geoids Based upon a Simulation[J]. Journal of Geodesy, 2007, 81(1): 67-80
(  0) 0) |
| [5] |
Pail R. CHAMP-, GRACE-, GOCE-Satellite Projects[A]//Grafarend E. Encyclopedia of Geodesy[M]. Cham: Springer, 2015
(  0) 0) |
| [6] |
Jäggi A, Beutler G, Mervart L. GRACE Gravity Field Determination Using the Celestial Mechanics Approach-First Results[A]//Mertikas S P. Gravity, Geoid and Earth Observation[M]. Heidelberg: Springer, 2010
(  0) 0) |
| [7] |
陈俊平, 王解先. GPS定轨中的太阳辐射压模型[J]. 天文学报, 2006, 47(3): 310-319 (Chen Junping, Wang Jiexian. Solar Radiation Pressure Models for the GPS Satellites[J]. Acta Astronomica Sinica, 2006, 47(3): 310-319 DOI:10.3321/j.issn:0001-5245.2006.03.009)
(  0) 0) |
| [8] |
Beutler G, Jäggi A, Hugentobler U, et al. Efficient Satellite Orbit Modelling Using Pseudo-Stochastic Parameters[J]. Journal of Geodesy, 2006, 80(7): 353-372 DOI:10.1007/s00190-006-0072-6
(  0) 0) |
| [9] |
Guo J L, Hu M, Zhao Q L, et al. Reducing Influence of Gravity Model Error in Precise Orbit Determination of Low Earth Orbit Satellites[J]. Geo-Spatial Information Science, 2007, 10(2): 105-110 DOI:10.1007/s11806-007-0055-7
(  0) 0) |
| [10] |
韩保民, 朱秀英. 伪随机脉冲估计及其在简化动力学定轨中的应用[J]. 武汉大学学报:信息科学版, 2007, 32(5): 466-469 (Han Baomin, Zhu Xiuying. Estimation of Pseudo-Stochastic Pulses and Their Applications in Reduced-Dynamic Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 466-469)
(  0) 0) |
| [11] |
赵春梅, 程鹏飞. 基于伪随机脉冲估计的简化动力学卫星定轨方法[J]. 宇航学报, 2011, 32(4): 762-766 (Zhao Chunmei, Cheng Pengfei. Reduced-Dynamics Satellite Orbit Determination Based on Pseudo-Stochastic Pulse Estimation[J]. Journal of Astronautics, 2011, 32(4): 762-766 DOI:10.3873/j.issn.1000-1328.2011.04.009)
(  0) 0) |
| [12] |
刘伟平, 郝金明, 田英国, 等. 一种伪随机脉冲的快速参数估计方法[J]. 武汉大学学报:信息科学版, 2015, 40(11): 1487-1492 (Liu Weiping, Hao Jinming, Tian Yingguo, et al. Fast Parameter Estimation for Pseudo-Stochastic Pulse[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1487-1492)
(  0) 0) |
| [13] |
田英国, 郝金明, 谢建涛, 等. SWARM卫星星载GPS精密定轨方法及精度分析[J]. 测绘科学技术学报, 2016, 33(5): 452-457 (Tian Yingguo, Hao Jinming, Xie Jiantao, et al. SWARM Precise Orbit Determination and Accuracy Analysis Using Onboard GPS Data[J]. Journal of Geomatics Science and Technology, 2016, 33(5): 452-457)
(  0) 0) |
| [14] |
闫志闯. GRACE卫星精密轨道确定与一步法恢复地球重力场[D].郑州: 信息工程大学, 2015 (Yan Zhichuang. Precise Orbit Determination and the Earth Gravity Field Recovery by One Step Method for GRACE[D]. Zhengzhou: Information Engineering University, 2015) http://cdmd.cnki.com.cn/Article/CDMD-90005-1016058452.htm
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

