激光跟踪仪具有测距精度高、测量速度快、动态高效等优点,广泛应用于航空航天、汽车、飞机等装配领域。激光跟踪仪的距离测量精度理论上可以达到μm级,但在应用过程中往往受制于装配现场气象条件。装配现场热源较多、温度分布不均匀[1],无论是IFM还是ADM,温度对测距精度的影响均不可忽略[2],温度影响约占所有气象参数影响量的92%,温度每变化约1.1 ℃,将引起约10-6的折射率变化[3-4]。
在实际应用中,激光跟踪仪数字化气象工作站可采集温度等气象参数,对测站端实时的气象进行改正,进而对距离观测值进行修正。对于装配制造而言,不能用某一点的温度值代表整条测线的实际温度值,应该是激光跟踪仪在测线上无数个温度因子的积分平均值,但该积分平均值在实际测量中不可能得到[5]。因此,若要提高激光跟踪仪的测量精度,需要对环境气象参数尤其是对测距影响较大的温度因子进行测距积分改正。本文以温度因子为研究对象,提出激光跟踪仪分段积分测距改正方法,建立分段积分测距改正模型,为装配现场的测距温度梯度改正提供理论支撑,有助于提高飞机等装配制造的精度。
1 分段积分测距改正模型常用的折射率公式有Barrel & Sears公式、Edlen-1966公式[6]、Edlen-1994公式[7]、Edlen-1995公式[8]、Ciddor & Hill公式[9]、Rugger公式[10]等。其中,Barrel & Sears公式和Edlen-1966公式一般用在室外对测量精度要求不高的情况,而Edlen-1994公式、Edlen-1995公式和Ciddor & Hill公式一般用在室内对测量精度要求较高的情况[2]。本文从精度和实用性两方面考虑采用Edlen-1995公式,标准状态下的大气折射率为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {n - 1} \right)_s} \times {10^8} = \\ 8\;342.54 + \frac{{2\;406\;147}}{{130 - {\sigma ^2}}} + \frac{{15\;998}}{{38.9 - {\sigma ^2}}} \end{array} $ | (1) |
式中,空气的标准温度为t=15 ℃、气压为P=101 325 Pa,CO2的含量为x=0.03%。
当温度和气压发生变化时:
| $ \begin{array}{l} \;\;\;{\left( {n - 1} \right)_{tp}} = \frac{{{{\left( {n - 1} \right)}_s} \times P}}{{96\;095.43}} \times \\ \frac{{1 + {{10}^{ - 8}} \times \left( {0.601 - 0.009\;72t} \right)}}{{1 + \alpha t}} \end{array} $ | (2) |
式中,α=1/273.16,为空气膨胀系数。
假设装配现场温度为t, 大气压强为P,不考虑湿度的影响,标准计量环境状态参数为:t=20 ℃,P=101 325 Pa。将其代入式(1)、式(2),得到气象改正公式:
| $ \begin{array}{l} {\rm{ppm}} = 271.687 - 291.580 \times \\ \frac{{1 + {{10}^{ - 8}}\left( {0.601 - 0.009\;72t} \right)}}{{1 + \alpha t}} \end{array} $ | (3) |
ppm为气象改正中按距离成比例的部分,单位是10-6。
1.1 两点积分测距改正模型当在现场仅获取测站与镜站的温度值时,设测站与镜站的距离为S(图 1),沿测线x方向上的温度不相等,且为x的函数。考虑到小范围内温度呈线性变化,则测线上温度随距离变化的直线方程为:
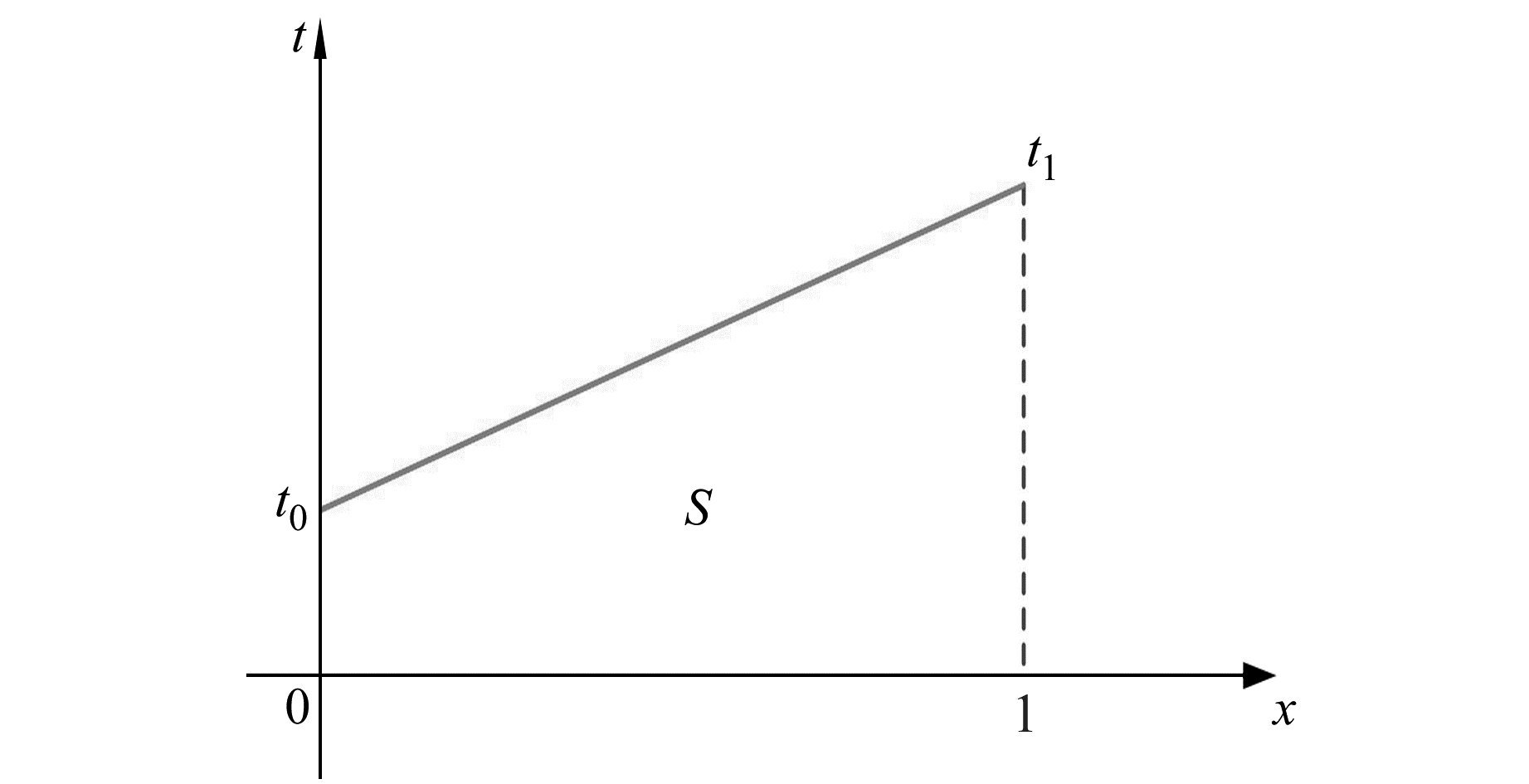
|
图 1 两点温度分布示意图 Fig. 1 Two-point temperature distribution diagram |
| $ t = \frac{{{t_1} - {t_0}}}{S}x + {t_0} $ | (4) |
将测段S细分为S1, S2, …Sn,当n趋于无穷大时,距离改正量以积分形式表示为:
| $ \begin{array}{l} D = \smallint _0^S{\rm{ppm}}\left( t \right){\rm{d}}x = \smallint _0^S[271.687 - 291.580 \times \\ \;\;\;\;\;\;\frac{{1 + {{10}^{ - 8}}\left( {0.601 - 0.009\;72t} \right)}}{{1 + \alpha t}}]{\rm{d}}x \end{array} $ | (5) |
将式(4)代入式(5)得:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\Delta D = 271.687S - \\ \frac{{291.580(1 + {{10}^{ - 8}}(0.601 - 0.009\;72{t_0}))S}}{{\alpha ({t_1} - {t_0})}} \times \\ \;\;\;\;\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}} + 2.831\;456\;7 \times {10^{ - 8}} \times \\ \;\;\;\;\;\;\frac{S}{\alpha }\left( {1 - \frac{{1 + \alpha {t_0}}}{{\alpha ({t_1} - {t_0})}}\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}}} \right) \end{array} $ | (6) |
即两点积分改正模型为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{\rm{ppm}} = \frac{{\Delta D}}{S} = 271.687 - \\ \frac{{291.580(1 + {{10}^{ - 8}}(0.601 - 0.009\;72{t_0}))}}{{\alpha ({t_1} - {t_0})}} \times \\ \;\;\;\;\;\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}} + 2.831\;456\;7 \times {10^{ - 8}} \times \\ \;\;\;\;\;\;\;\frac{1}{\alpha }\left( {1 - \frac{{1 + \alpha {t_0}}}{{\alpha ({t_1} - {t_0})}}\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}}} \right) \end{array} $ | (7) |
当在现场不仅测量测站与镜站的温度值,还测量测站与镜站中点的温度值时,假设现场温度呈线性变化,测站与镜站的距离为S(图 2),则测段内温度随距离变化的直线方程为:

|
图 2 均匀三点温度分布示意图 Fig. 2 Uniform three-point temperature distribution diagram |
| $ \left\{ \begin{array}{l} t = \frac{{2({t_1} - {t_0})}}{S}x + {t_0}\\ t = \frac{{2({t_2} - {t_1})}}{S}x + 2{t_1} - {t_2} \end{array} \right. $ | (8) |
同理可得,三点等距积分改正模型为:
| $ {\rm{ppm}} = \frac{1}{2}{\rm{pp}}{{\rm{m}}_{0, 1}} + \frac{1}{2}{\rm{pp}}{{\rm{m}}_{1, 2}} $ | (9) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{\rm{pp}}{{\rm{m}}_{0, 1}} = 271.687 - \\ \frac{{291.580(1 + {{10}^{ - 8}}(0.601 - 0.009\;72{t_0}))}}{{\alpha ({t_1} - {t_0})}} \times \\ \;\;\;\;\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}} + 2.831\;456\;7 \times {10^{ - 8}} \times \\ \;\;\;\;\;\;\frac{1}{\alpha }\left( {1 - \frac{{1 + \alpha {t_0}}}{{\alpha ({t_1} - {t_0})}}\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}}} \right) \end{array} $ | (10) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{pp}}{{\rm{m}}_{1, 2}} = \\ - \frac{{291.580(1 + {{10}^{ - 8}}(0.601 - 0.009\;72(2{t_1} - {t_2})))}}{{\alpha ({t_2} - {t_1})}} \times \\ \;\;\;\;\;\;\;\;\;\;\ln \frac{{1 + \alpha {t_2}}}{{1 + \alpha {t_1}}} + 2.831\;456\;7 \times {10^{ - 8}} \times \\ \;\;\;\frac{1}{\alpha }\left( {1 - \frac{{1 + \alpha (2{t_1} - {t_2})}}{{\alpha ({t_2} - {t_1})}}\ln \frac{{1 + \alpha {t_2}}}{{1 + \alpha {t_1}}}} \right) + 271.687 \end{array} $ | (11) |
一般情形下,在一条测线上布设n+1个温度传感器,将测线分为n段,每段距离分别为S1, S2, …Sn(图 3)。

|
图 3 多点温度分布示意图 Fig. 3 Multi-point temperature distribution diagram |
同理可得多点测距积分改正模型为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{pp}}{{\rm{m}}_{0, n}} = \\ \frac{{{S_1}}}{S}{\rm{pp}}{{\rm{m}}_{0, 1}} + \frac{{{S_2}}}{S}{\rm{pp}}{{\rm{m}}_{1, 2}} + \cdots + \frac{{{S_n}}}{S}{\rm{pp}}{{\rm{m}}_{n - 1, n}} \end{array} $ | (12) |
式中,S=S1+S2+…+Sn, 则:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\rm{pp}}{{\rm{m}}_{0, 1}} = 271.687 - \\ \frac{{291.580(1 + {{10}^{ - 8}}(0.601 - 0.009\;72{t_0}))}}{{\alpha ({t_1} - {t_0})}} \times \\ \;\;\;\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}} + 2.831\;456\;7 \times {10^{ - 8}} \times \\ \;\;\;\frac{1}{\alpha }\left( {1 - \frac{{1 + \alpha {t_0}}}{{\alpha ({t_1} - {t_0})}}\ln \frac{{1 + \alpha {t_1}}}{{1 + \alpha {t_0}}}} \right) \end{array} $ | (13) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{pp}}{{\rm{m}}_{i, i + 1}} = \\ - \frac{{291.580(1 + {{10}^{ - 8}}(0.601 - 0.009\;72(2{t_i} - {t_{i + 1}})))}}{{\alpha ({t_{i + 1}} - {t_i})}}\\ \;\;\;\;\;\;\;\; \times \ln \frac{{1 + \alpha {t_{i + 1}}}}{{1 + \alpha {t_i}}} + 2.831\;456\;7 \times {10^{ - 8}} \times \\ \;\;\frac{1}{\alpha }\left( {1 - \frac{{1 + \alpha (2{t_i} - {t_{i + 1}})}}{{\alpha ({t_{i + 1}} - {t_i})}}\ln \frac{{1 + \alpha {t_{i + 1}}}}{{1 + \alpha {t_i}}}} \right) + 271.687 \end{array} $ | (14) |
式中,i=1, 2, …n-1。
2 实验和分析为验证本文提出的分段积分测距改正模型的正确性,采用Radian激光跟踪仪进行单测线温度测距改正实验,分为倾斜、水平2组实验。
在实验过程中,为避免现场环境震动,尽量减少人员走动,确保激光跟踪仪与靶球基座处于稳定的环境。同时,要保证密闭空间内的气压、湿度、空气扰动等参数随着温度的升高不发生较大的变化,以排除其对实验结果的影响。
2.1 倾斜单测线实验实验现场配置如图 4所示,激光跟踪仪与靶球相距约7.866 m,激光束通过密闭空间投射到靶球上,在光路中点位置以大功率电灯泡作为热源,对整个密闭空间进行加热,模拟测线上的温度分布。测线光路附近布设4个温度传感器,测量精度为±0.2 ℃。

|
图 4 倾斜单测线实验现场配置 Fig. 4 Field configuration of tilt single line experiment |
在实验的开始阶段,调节现场温度、气压、湿度(水气压)等气象参数近似为t=20 ℃、P=101 325 Pa、f0= 101 325/76 Pa。在近似标准的气象状态下,测量测站到镜站的距离并进行相应的气象改正,多次测量得到平均值为7 866.521 6 mm,以此作为距离的基准值。
打开热源进行密闭空间加热,记录现场温度及测距值的变化,每组温度节点采集30个数据,最后取平均值,共进行21次实验,部分结果见表 1。
|
|
表 1 倾斜单测线实验测量值 Tab. 1 Tilt single line experimental measurements |
实验现场配置如图 5所示,激光跟踪仪与靶球相距约7.539 m,采用相同的方法,多次测量得到平均值为7 539.465 1 mm,以此作为距离的基准值。打开热源进行密闭空间加热,记录现场温度及测距值的变化,每组温度节点采集30个数据,共进行26次实验,部分测量结果见表 2。

|
图 5 水平单测线实验现场配置 Fig. 5 Field configuration of horizontal single line experiment |
|
|
表 2 水平单测线实验测量值 Tab. 2 Horizontal single line experimental measurements |
对2组实验数据的结果分别采用单点法、两点均值法、分段积分法进行改正,比较测距改正值与基准值的差值,结果见表 3和4。
|
|
表 3 倾斜单测线实验测距改正值与基准值差值 Tab. 3 The difference between range correction value and datum value of tilt single line experiment |
|
|
表 4 水平单测线实验测距改正值与基准值差值 Tab. 4 The difference between range correction value and datum value of horizontal single line experiment |
图 6为不同测距改正方法差值比较。由图可知,在实验开始阶段,各点温度值差异较小,单点法、两点均值法及分段积分法改正得到的差值都比较小;随着热源温度的升高,各温度测量点之间的温差变大,采用单点法和两点均值法进行测距值改正时差值变大,并且差值会随着温差的增大愈发增大;分段积分改正方法的改正效果明显优于另外2种方法,其改正值与基准值的差值在15 μm以内,能够有效地削弱温度梯度造成的影响。
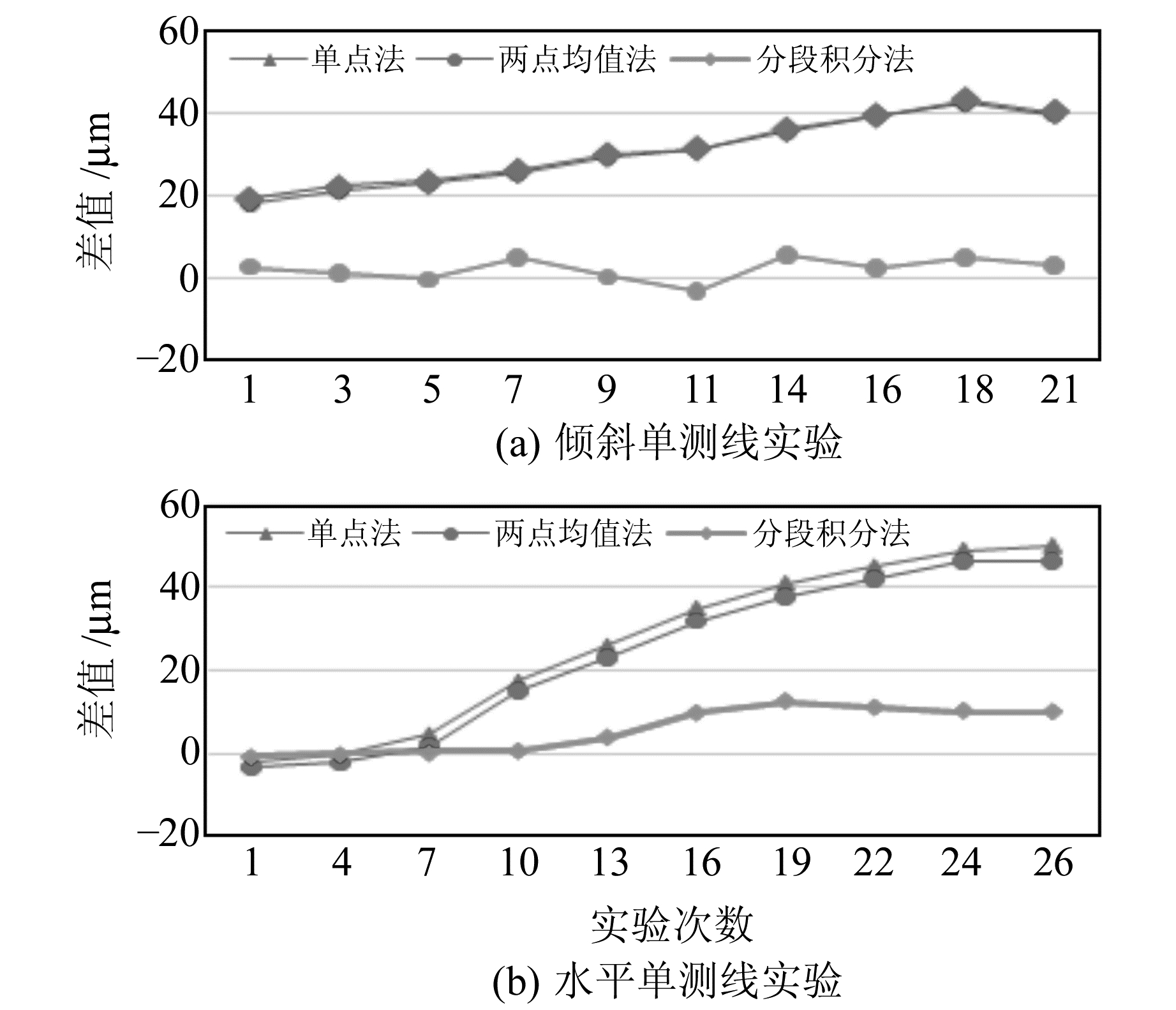
|
图 6 不同测距改正方法差值比较 Fig. 6 Comparison of different range correction methods |
考虑到在测量实验过程中,温度、气压、湿度、震动等影响因子并非完全可控,测线温度的测量值只是测线附近的温度等效值,温度传感器本身的精度及由于测量、传输等在时间上的滞后性等因素,都会造成一定的测量误差。虽然采取气压、湿度等相关因子调节措施,但现场环境会不可避免地随着温度的升高发生变化,外界的轻微震动也会影响测量值的变化。因此,分段积分测距改正模型并不能完全消除现场环境温度梯度的影响,但可以极大地削弱其对测量值造成的影响,通过实验分析验证了分段积分改正模型的准确性。
3 实际应用与分析分段积分测距改正模型能够有效削弱温度梯度对测距的影响,但在实际应用中,如何有效测量测线上的温度值是急需解决的问题。
在装配现场均匀布设若干温度传感器,并对局部温度特征点进行测量,建立覆盖整个装配车间的温度全局控制网络,实时监控现场的温度参数,图 7为装配现场传感器配置。
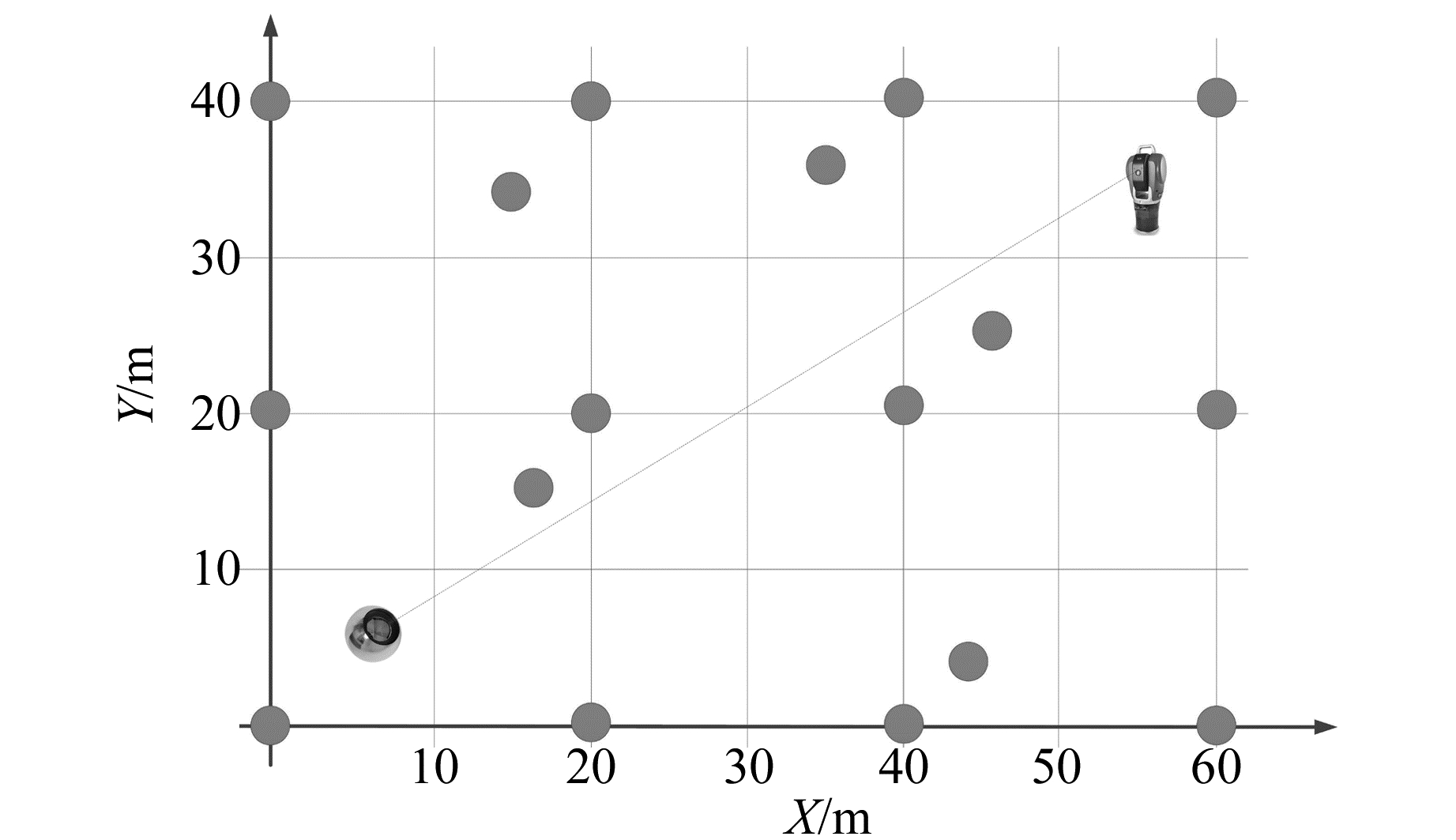
|
图 7 装配现场传感器配置 Fig. 7 Sensor configuration at assembly site |
温度控制网络可以获取有限离散点的温度值,对于未测量温度值的点,需要通过附近点的温度值和适当的空间内插值函数来计算其温度值,从而建立装配车间温度场热力分布图(图 8)。
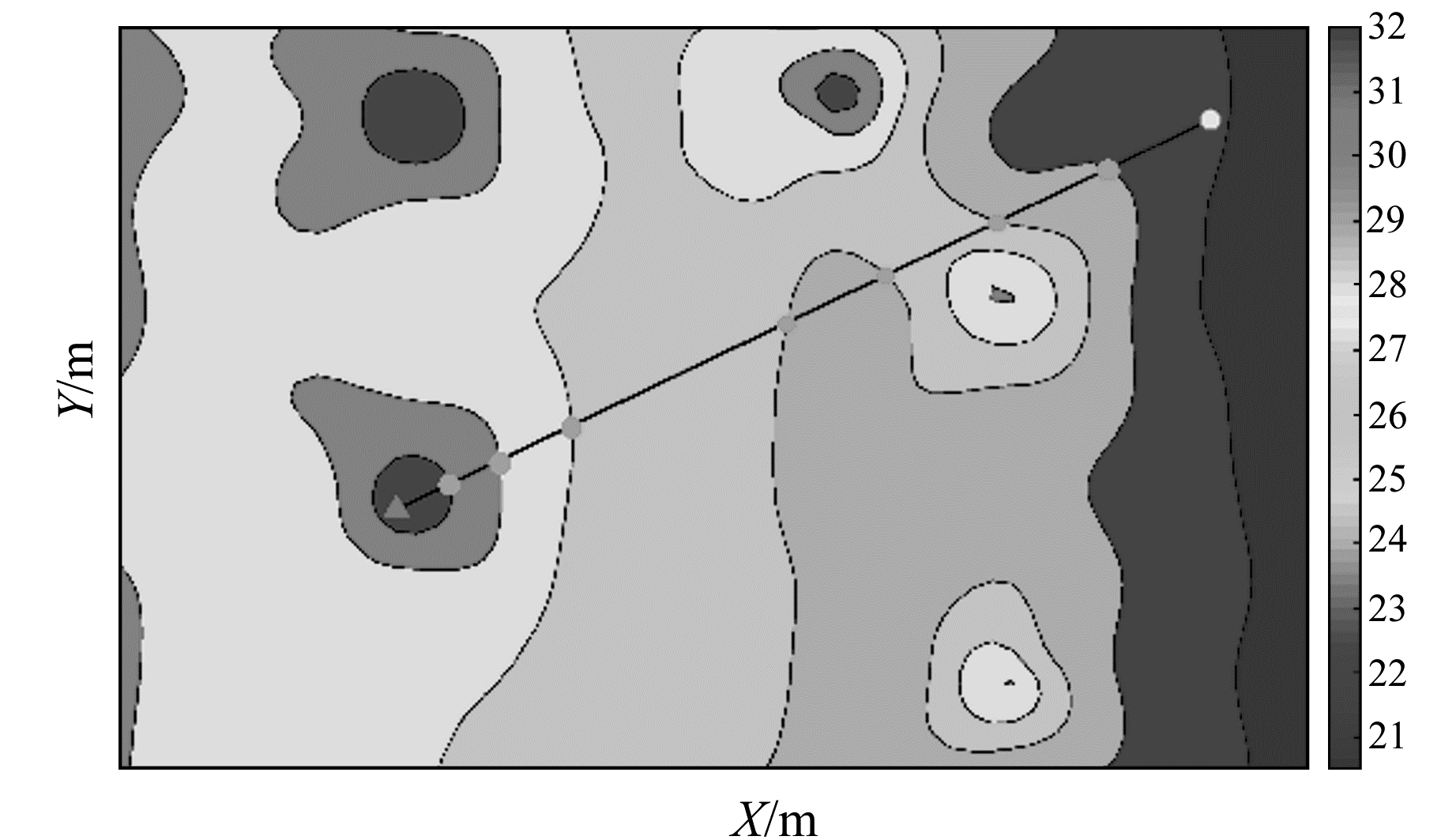
|
图 8 装配现场热力分布 Fig. 8 Assembly site thermal distribution |
在激光跟踪仪测量过程中,通过提取测线与等温线交点的温度值进行分段积分测距改正,提高激光跟踪仪数据测量成果,进而提高装配制造精度。
4 结语本文提出的激光跟踪仪分段积分测距改正方法能够有效地削弱装配现场温度梯度的影响,极大地提高装配制造的精度,特别适用于装配环境场中温度差异较大、温度场分布不均匀的情况。但该模型只对测距影响较大的温度因子进行积分测距改正,没有考虑气压、湿度、CO2等微小因子的影响,对于装配现场气压、湿度分布不均匀、波动范围较大的情况,可采用类似的方法,通过布设湿度、气压传感器,对所有因子进行积分测距改正。
| [1] |
张俐, 王炜辰. 基于飞机装配的热变形误差分析方法[J]. 机械工程与自动化, 2017(1): 4-6 (Zhang Li, Wang Weichen. Thermal Deformation Errors Analysis Method Based on Aircraft Assembly[J]. Mechanical Engineering and Automation, 2017(1): 4-6 DOI:10.3969/j.issn.1672-6413.2017.01.002)
(  0) 0) |
| [2] |
王亚伟, 周维虎, 王中宇, 等. 激光跟踪测量系统大气折射率修正方法[J]. 光电子技术, 2011, 31(2): 83-86 (Wang Yawei, Zhou Weihu, Wang Zhongyu, et al. Correction Method of Air Refractivity for Laser Tracking Measurement System[J]. Optoelectronic Technology, 2011, 31(2): 83-86)
(  0) 0) |
| [3] |
欧阳麟桦, 方长远, 严峻. 环境因素对测量塔全站仪定位精度的影响研究[J]. 测绘地理信息, 2013, 38(3): 67-70 (Ouyang Linhua, Fang Changyuan, Yan Jun. Study on Impact of Environmental Factors on Measurement of Total-Station Positioning[J]. Journal of Geomatics, 2013, 38(3): 67-70)
(  0) 0) |
| [4] |
于成浩, 柯明, 赵振堂. 提高激光跟踪仪测量精度的措施[J]. 测绘科学, 2007, 32(2): 54-56 (Yu Chenghao, Ke Ming, Zhao Zhentang. Measures to Improve Measurement Accuracy of Laser Tracker[J]. Science of Surveying and Mapping, 2007, 32(2): 54-56 DOI:10.3771/j.issn.1009-2307.2007.02.019)
(  0) 0) |
| [5] |
范百兴.激光跟踪仪高精度坐标测量技术研究与实现[D].郑州: 信息工程大学, 2013 (Fan Baixing. Research and Realization of the High Precision Coordinate Measurement Technique Using Laser Tracker[D]. Zhengzhou: Information Engineering University, 2013) http://cdmd.cnki.com.cn/Article/CDMD-90005-1016058201.htm
(  0) 0) |
| [6] |
Birch K P, Downs M J. An Updated Edlén Equation for the Refractive Index of Air[J]. Metrologia, 1993, 30(3): 155-159 DOI:10.1088/0026-1394/30/3/004
(  0) 0) |
| [7] |
Korpelainen V, Lassila A. Acoustic Method for Determination of the Effective Temperature and Refractive Index of Air in Accurate Length Interferometry[J]. Optical Engineering, 2004, 43(10): 9-15
(  0) 0) |
| [8] |
Birch K P, Downs M J. Correction to the Updated Edlén Equation for the Refractive Index of Air[J]. Metrologia, 1994, 31(4): 315-319 DOI:10.1088/0026-1394/31/4/006
(  0) 0) |
| [9] |
Ciddor P E, Hill R J. Refractive Index of Air.2. Group Index[J]. Applied Optics, 1999, 38(9): 1663-1667 DOI:10.1364/AO.38.001663
(  0) 0) |
| [10] |
Birch K P, Downs M J. The Results of a Comparison between Calculated and Measured Values of the Refractive Index of Air[J]. Journal of Physics E: Scientific Instruments, 1988, 21(7): 694-699 DOI:10.1088/0022-3735/21/7/015
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

