自2002年GRACE卫星计划实施以来,GRACE时变重力场一直是国内外大地测量学者们研究的热门领域,已经取得不少重大科研成果[1-6]。由于GRACE重力场模型高阶项存在较大误差,其时变重力场会出现明显的南北条带误差,因此需要采用一定的滤波方法以削弱条带误差的影响。常用的方法是对球谐位系数直接进行频谱滤波,如高斯滤波和去相关滤波等,但这些方法在削弱条带误差影响的同时也会抑制真实的质量变化信号[7]。Wouters等[8]提出对球谐位系数进行经验正交函数(empirical orthogonal function,EOF)滤波,相比其他滤波方法,该方法的结果能更好地反映真实的地球物理信息,但消除条带的效果稍差。为了在削弱条带影响的同时尽可能地保留真实的质量变化信号,本文针对经验正交函数滤波方法进行改良,提出一种基于经验正交函数和去相关滤波的组合滤波方法,并利用真实GRACE数据验证其削弱南北条带误差的能力,分别从反演结果、误差分布及其均方根(RMS)的角度比较滤波效果。结果显示,组合滤波方法削弱南北条带误差的能力要优于经验正交函数滤波方法和去相关滤波方法。利用模拟数据验证其保留真实地球物理信号的能力,并从反演结果残差的RMS角度进行比较分析,组合滤波方法的RMS最小,优于以上2种已有的滤波方法。多种分析结果表明,该组合方法结合了两者的优点,能够在削弱条带影响的同时尽可能地保留真实信号。
1 基本原理 1.1 等效水高计算利用GRACE数据处理机构发布的RL05时变地球重力场模型计算地球质量变化,以等效水高表示为[9]:
| $ \begin{array}{l} \Delta H\left( {\theta , \lambda } \right) = \frac{{a{\rho _{{\rm{ave}}}}}}{{3{\rho _w}}}\mathop \sum \limits_{l = 0}^\infty \mathop \sum \limits_{m = 0}^l {{\bar P}_{lm}}\left( {\cos \theta } \right){W_l}\frac{{2l + 1}}{{1 + {k_l}}} \times \\ \;\;\;\;\;\;\;\;\;(\Delta {{\bar C}_{lm}}\cos \left( {m\lambda } \right) + \Delta {{\bar S}_{lm}}\sin \left( {m\lambda } \right)) \end{array} $ | (1) |
式中,a为地球平均半径,ρave为地球平均密度,ρw为水的密度,l与m分别为球谐位系数对应的阶和次,Plm(cosθ)为完全规格化的勒让德(Legendre)函数,kl为考虑地球弹性形变的负荷勒夫数(LOVE数),ΔClm与ΔSlm为每月球谐位系数的变化值,θ为地心余纬,λ为地心经度,Wl为高斯滤波函数。值得注意的是,仅采用高斯滤波并不能完全削弱条带误差的影响,需结合其他方法,如文献[10]的去相关滤波方法。
1.2 经验正交函数分析方法经验正交函数分析方法又称为主成分分析(principal components analysis, PCA),是一种基于二阶统计信息的信号分解方法[11]。设每个历元含有p个观测点,n个历元的数据可以存储在一个n×p的矩阵X中,则矩阵X的PCA分解可以表示为:
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{E}}^{\rm{T}}} $ | (2) |
式中,E为经验正交函数,可以对X的协方差矩阵C进行特征值分解,得到P=XE,储存着主成分。为降低数据集的维度,可以将主要模式保留下来,再对其进行重构,即
| $ \mathit{\boldsymbol{X}} \cong {\mathit{\boldsymbol{X}}_j} = {\mathit{\boldsymbol{P}}_j}\mathit{\boldsymbol{E}}_j^{\rm{T}}, j < \min \left( {n, p} \right) $ | (3) |
在经验正交函数滤波方法中,将每个模式对应的时间序列进行白噪声测试,常采用Kolmogorov-Smirnov检验(KS2检验)[12],被判别为白噪声的时间序列将不会用于重构。
2 基于经验正交函数的GRACE滤波方法及其改进利用经验正交函数对GRACE球谐位系数进行滤波处理,最早由Wouters等[8]和Schrama等[13]提出,其核心在于对不同历元同一次的球谐位系数进行主成分分析。本文采用2003-01~2013-12共124个月的GRACE时变地球重力场模型作为参考数据,数据来源于CSR,其间共缺失8个月的数据。根据上述经验正交函数方法,对GRACE时变地球重力场模型进行处理,并与其他滤波方法对比。几种方法在2008-03全球范围内的等效水高变化量如图 1所示,其中所有方法的高斯滤波半径均为300 km,去相关滤波方法采用P4M6[14-15]。

|
图 1 2008-03不同滤波方法的等效水高 Fig. 1 Equivalent water heights of different filtering methods in March, 2008 |
从图 1可以看出,当高斯滤波半径为300 km时,3种方法均可以识别出一定的地球物理信号,特别是在亚马孙流域,但条纹还是比较明显。去相关滤波方法去除南北条带误差的能力最好,特别是在高纬地区,经验正交函数滤波方法次之,但去相关滤波方法在部分地区的信号强度要弱于经验正交函数滤波方法,后者保留信号的能力要更好一些。为更好地去除条带误差并保留信号,针对经验正交函数滤波方法和去相关滤波方法的特点,通过综合对比分析及不断实验,提出将2种滤波方法结合进行组合滤波的改进策略,即在经验正交函数滤波之后,再对球谐位系数进行一次去相关滤波,但在进行经验正交函数滤波时,只对次数为0~55的系数进行滤波,其他系数保持不变。文中采用P4M6方法,可以在一定程度上减少有效信息的损失,同时削弱条带误差的影响。
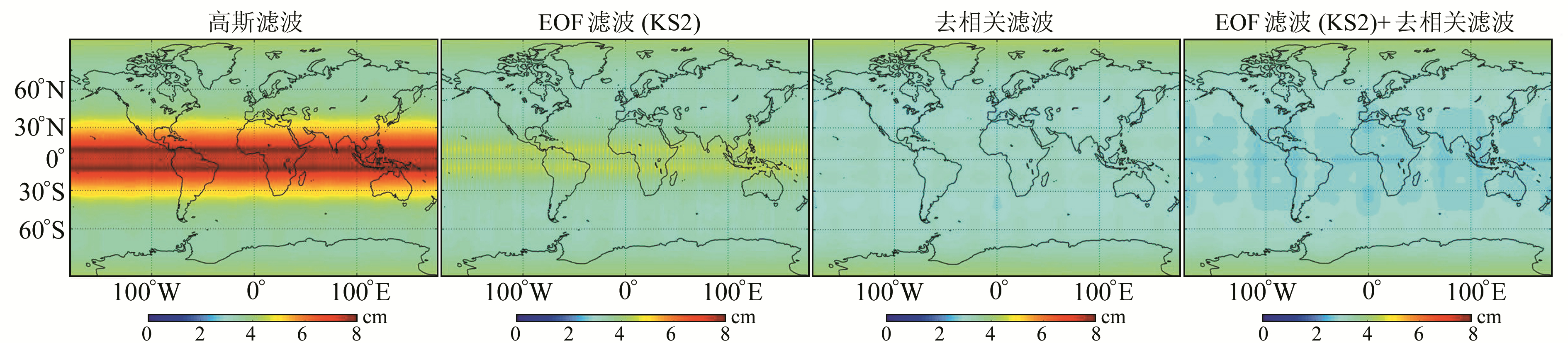
3 结果对比分析为了从误差的角度比较各种方法的效果,利用Wahr等[16]提出的方法,在球谐位系数中扣除线性项、1 a项和0.5 a项等变化,将残差作为对应球谐位系数的误差,并利用误差传播定律得到等效水高误差的全球分布,结果见图 2。
|
图 2 几种方法计算得到的误差全球分布 Fig. 2 Global distribution of errors calculated by several methods |
从图 2可以看出,去相关滤波等针对条带误差的滤波方法可以大幅降低误差。误差的分布在空间上具有相同的特征,即赤道地区的误差较大,两极地区相对较小,这主要是由于GRACE卫星为近极圆轨卫星,观测数据在两极较为密集,在赤道地区相对较少。组合滤波方法的误差小于经验正交函数滤波方法和去相关滤波方法。为了定量地进行比较分析,将误差在空间上的RMS作为分析滤波效果的指标之一,不同高斯滤波半径下的RMS如表 1(单位mm)所示。由表 1可知,在进行针对条带的滤波后,RMS都有一定程度的下降,当滤波方法固定时,RMS会随着滤波半径的增大而减小。与仅进行高斯滤波的方法相比,高斯滤波半径越小,各种去相关滤波方法的RMS下降幅度越大,当半径足够大时,RMS下降幅度并不明显,这是因为随着滤波半径的增加,地球物理信号的强度会变得越来越弱,过大的滤波半径降低了反演结果的空间分辨率,在削弱误差影响的同时也抑制了有效的地球物理信号,此时进行去相关滤波已无太大意义。但当高斯滤波半径为0时,经验正交函数方法的RMS要远大于去相关滤波方法,说明经验正交函数滤波方法的效果与高斯滤波半径有关,当滤波半径足够小时,滤波效果不会太明显。从表 1还可看出,在没有高斯滤波的条件下,组合滤波方法的RMS最小,说明直接对原始数据进行滤波时,组合滤波方法过滤噪声的效果最好。当然RMS只能作为比较不同滤波方法的指标之一,在具体的比较中还需与其他的指标或判别方法相结合,从而得到最合理的结果。
|
|
表 1 各种方法在不同高斯滤波半径下的RMS Tab. 1 RMS with different methods under different Gaussian filtering radius |
一般而言,当高斯滤波半径固定时,如果只进行高斯滤波而不进行去相关滤波,得到的结果除了真实的地球物理信号外,必然包含有条带误差。如果在进行高斯滤波的同时还进行了针对条带的滤波,其结果主要为真实信号,当然也带有一部分条带误差。如果去条带足够彻底,那么两者之差应该只包含条带误差的信息。基于此,可以通过两者之差来判定去条带效果的好坏。计算高斯滤波与其他3种方法结果的差值,结果见图 3。

|
图 3 高斯滤波与其他滤波方法的差值 Fig. 3 The difference between the results calculated by Gaussian filtering and other filtering methods |
由图 3可知,经验正交函数滤波方法所对应的图像中条带信号强度与另外2个相比要弱些,且在80°~90°的高纬地区,基本上看不到条带的存在,而另外2种方法相比区别不大。经验正交函数滤波方法在一定的条件下可以削弱条带误差的影响,但效果比另外2种要差一些,特别是在高纬地区,这也与图 1中结果相印证。
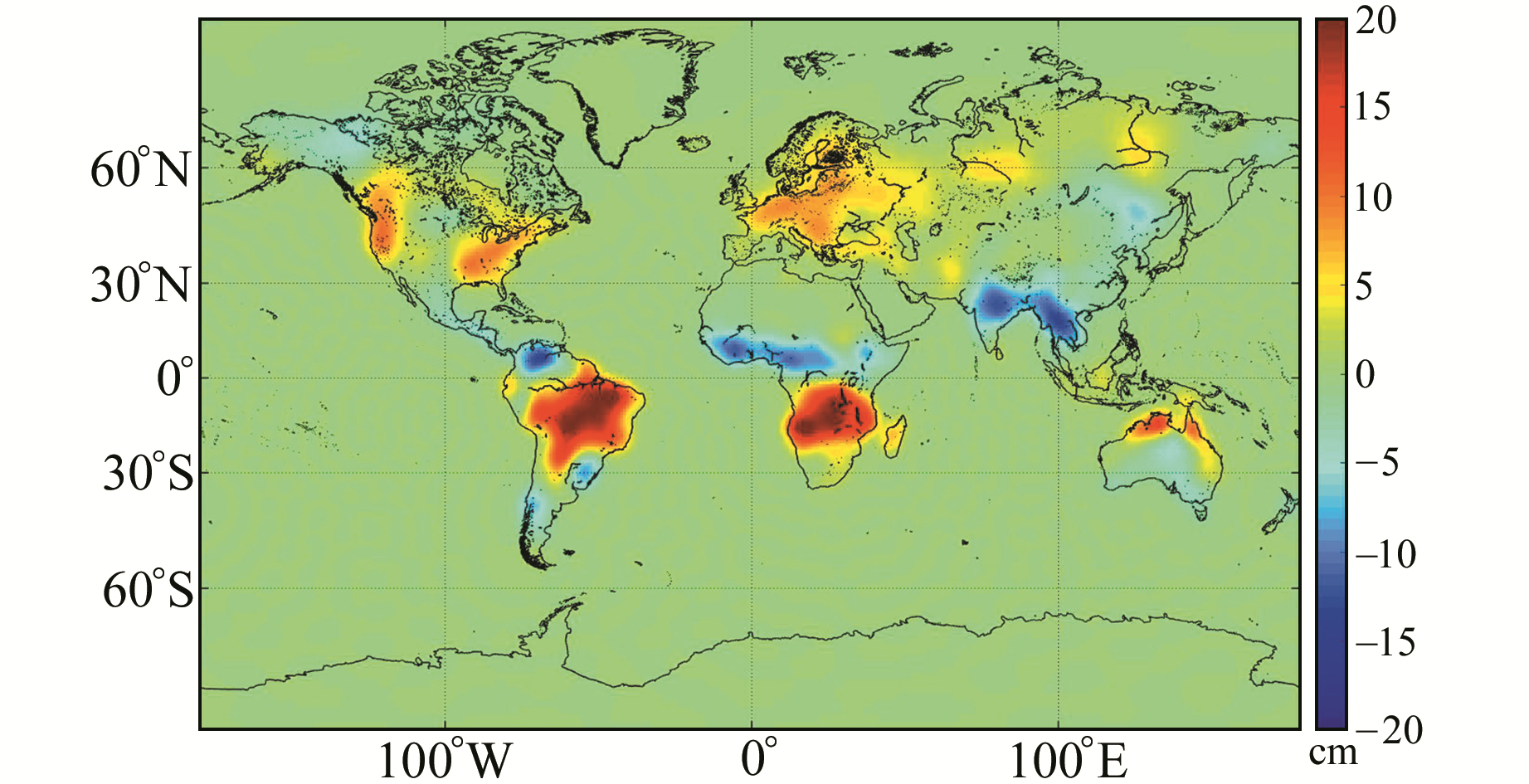
前文主要探讨了3种方法去除条带的能力,无法直观地比较其保留有效地球物理信号的能力。为了对其进行分析,最简单的方法就是将滤波之后的结果与全球实际变化进行比较,但完全真实的地球物理信号基本上无法得到。为此,本文设计了一个模拟实验,利用GLDAS(global land data assimilation system)水文模式的土壤湿度变化来替代现实中的水储量变化,并将其作为原始模拟信号转换为球谐位系数的形式,类比GRACE数据,利用高斯滤波计算其等效水高。图 4即为2008-03高斯滤波半径为300 km时的等效水高。
|
图 4 由NOAH数据计算得到的2008-03等效水高模拟值 Fig. 4 Simulated equivalent water height calculated from NOAH data in March, 2008 |
为了在模拟的全球等效水高中添加南北条带,将图 1中仅进行高斯滤波与去相关滤波方法的结果差值作为模拟的条带误差添加在图 4中。利用3种滤波方法对模拟数据的球谐位系数进行处理,计算得到的全球变化如图 5所示。图 5中第1行从左到右分别表示2008-03用3种方法计算得到的等效水高,第2行表示没有添加条带误差的原始模拟信号与3种滤波结果的差值。将3种方法的等效水高与原始模拟信号进行比较可以发现,经验正交函数滤波方法的结果与原始模拟信号最接近,组合滤波方法次之,去相关滤波方法最差,特别是在亚马孙流域等信号相对较强的地区。经验正交函数方法在信号强度上与模拟信号最为接近,但残存的条带也最为明显。比较图 5中第2行的图像,在3种方法残余的信号中,去相关方法最为明显,与组合方法的信号分布比较相似,但前者强度明显要大一些,特别是在赤道几内亚湾地区;经验正交函数方法依然出现了较为明显的条带,尤其是在高纬地区;其他2种方法分布比较均匀,这也与前文描述相互印证。

|
图 5 3种滤波方法的等效水高及其与等效水高模拟值的差值 Fig. 5 The equivalent water heights of the three filtering methods and their difference from the simulated equivalent water height |
为了定量地比较3种方法的结果与模拟信号的差异,分别计算其差值在空间上的RMS。一般而言,RMS越小表明该方法的结果与模拟信号相差越小,说明该方法保留实际信号的能力越强。3种方法的RMS分别为10.6 mm、11.0 mm和9.9 mm,其中,组合滤波方法的RMS最小,去相关滤波方法最大。由此可知,组合滤波方法的结果与模拟信号最为接近,保留实际信号的能力最好。
4 结语本文在经验正交函数滤波方法的基础上,提出改进的策略,即经验正交函数滤波与去相关滤波的组合滤波方法。对2003~2013年的GRACE数据进行滤波,从反演结果、误差分布及RMS可以发现,去相关滤波方法和组合滤波方法去除条带的能力较强。如果高斯滤波半径很小,经验正交函数方法的结果有时会不太理想,这是其局限性之一。利用模拟数据探究各方法保留真实信号的能力可知,组合滤波方法的RMS最小,保留真实信号的能力最好,经验正交函数方法次之,去相关滤波方法保留信号的能力较弱。经验正交函数方法也有局限性,其对GRACE球谐位系数时间序列的长度有一定的要求,如果时间序列很短,甚至只有1个月,滤波效果会很差,而去相关滤波对时间序列的长度没有要求。另外,经验正交函数方法对时间序列两端的月份滤波效果非常有限[8],这也是其局限性之一。本文的改进方法是由经验正交函数方法和去相关滤波组合得到,同样受到上述经验正交函数方法局限性的影响,但相较于单纯的经验正交函数方法,影响不是很大。由此可知,改良的组合方法继承了经验正交函数滤波方法与去相关滤波方法的优点,能够在削弱南北条带误差影响的同时,尽可能地保留真实信号。
| [1] |
Tapley B D, Bettadpur S, Ries J C, et al. GRACE Measurements of Mass Variability in the Earth System[J]. Science, 2004, 305(5683): 503-505 DOI:10.1126/science.1099192
(  0) 0) |
| [2] |
Chen J L, Wilson C R, Blankenship D, et al. Accelerated Antarctic Ice Loss from Satellite Gravity Measurements[J]. Nature Geoscience, 2009, 2(12): 859-862 DOI:10.1038/ngeo694
(  0) 0) |
| [3] |
Han S C, Shum C K, Bevis M, et al. Crustal Dilatation Observed by GRACE after the 2004 Sumatra-Andaman Earthquake[J]. Science, 2006, 313(5787): 658-662 DOI:10.1126/science.1128661
(  0) 0) |
| [4] |
Luo Z C, Li Q, Zhang K, et al. Trend of Mass Change in the Antarctic Ice Sheet Recovered from the Grace Temporal Gravity Field[J]. Science China Earth Science, 2011, 55(1): 76-82
(  0) 0) |
| [5] |
Matsuo K, Heki K. Time-Variable Ice Loss in Asian High Mountains from Satellite Gravimetry[J]. Earth and Planetary Science Letters, 2010, 290(1-2): 30-36 DOI:10.1016/j.epsl.2009.11.053
(  0) 0) |
| [6] |
Rodell M, Velicogna I, Famiglietti J S. Satellite-Based Estimates of Groundwater Depletion in India[J]. Nature, 2009, 460(7258): 999-1002 DOI:10.1038/nature08238
(  0) 0) |
| [7] |
许才军, 龚正. GRACE时变重力数据的后处理方法研究进展[J]. 武汉大学学报:信息科学版, 2016, 41(4): 503-510 (Xu Caijun, Gong Zheng. Review of the Post-Processing Methods on GRACE Time Varied Gravity Data[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4): 503-510)
(  0) 0) |
| [8] |
Wouters B, Schrama E J O. Improved Accuracy of GRACE Gravity Solutions through Empirical Orthogonal Function Filtering of Spherical Harmonics[J]. Geophysical Research Letters, 2007, 34(23): L23711
(  0) 0) |
| [9] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research:Solid Earth, 1998, 103(B12): 30205-30229 DOI:10.1029/98JB02844
(  0) 0) |
| [10] |
Swenson S, Wahr J. Post-Processing Removal of Correlated Errors in GRACE Data[J]. Geophysical Research Letters, 2006, 33(8): L08402
(  0) 0) |
| [11] |
Hyvärinen A. Survey on Independent Component Analysis[J]. Neural Computing Surveys, 1999, 2(4): 94-128
(  0) 0) |
| [12] |
Preisendorfer R W. Principal Component Analysis in Meteorology and Oceanography[M]. New York: Elsevier Science Ltd, 1988
(  0) 0) |
| [13] |
Schrama E J O, Wouters B, Lavallée D A. Signal and Noise in Gravity Recovery and Climate Experiment(GRACE) Observed Surface Mass Variations[J]. Journal of Geophysical Research, 2007, 112(B8): B8407 DOI:10.1029/2006JB004882
(  0) 0) |
| [14] |
Chen J L, Wilson C R, Tapley B D, et al. Antarctic Regional Ice Loss Rates from GRACE[J]. Earth and Planetary Science Letters, 2008, 266(1-2): 140-148 DOI:10.1016/j.epsl.2007.10.057
(  0) 0) |
| [15] |
Chen J L, Wilson C R, Tapley B D, et al. GRACE Detects Coseismic and Postseismic Deformation from the Sumatra-Andaman Earthquake[J]. Geophysical Research Letters, 2007, 34(13): L13302
(  0) 0) |
| [16] |
Wahr J, Swenson S, Velicogna I. Accuracy of GRACE Mass Estimates[J]. Geophysical Research Letters, 2006, 33(6): L06401
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


