2. 安徽省地震局,合肥市长江西路558号,230031
重力场是地球的基本物理场之一,其模型的构建是大地测量的研究目标。随着观测技术的不断发展,可利用的数据包括地表重力/GPS联合观测数据、卫星测高重力数据、船载测量重力数据及EGM2008地球重力场模型数据等。综合利用不同精度、不同分辨率和不同分布范围的重力数据,为局部重力场的优化提供可能。EGM2008模型数据覆盖全球,其中地面数据采集的覆盖面积占比高达83.8%,较以往模型精度更高,特别是在中国西部的川滇地区,利用其计算似大地水准面的精度能够达到24 cm[1]。但中国是重力专利数据区,在EGM2008模型构建时运用了地形推断的结果,中国大陆区域将近80%的区域模型值与实测值会产生10 mGal的差异,而在青藏高原地区标准差达到52.05 mGal[2]。地表重力/GPS联合观测数据获得的重力值相较于卫星观测数据,精度高出2个数量级,但分布极不均匀。
移去-恢复法作为经典多源数据融合方法,在GPS水准拟合中已有广泛的应用[3-4]。同时,该方法也广泛应用于局部重力场的优化,即采用EGM2008地球重力场模型作为移去-恢复法的参考场,通过拟合移去重力场模型后的残余重力,能够有效去除高频信息在拟合过程中的干扰。但移去-恢复法作局部重力场模型的优化时仅考虑了地理距离因素,地形的梯度同样会影响移去-恢复法的更新效果。
本文在常规拟合法的基础上引入地形梯度变量,改进经典移去-恢复法,从理论上优化局部重力场,并利用该算法对喜马拉雅东构造结及邻区的重力场进行校准。
1 移去-恢复法算法优化经典移去-恢复法理论模型中,重力异常能够分解为3个异常分量,分别为地球重力场模型的长波分量、地面重力异常的中波分量和地形改正对大地水准面的影响。移去-恢复法的核心思想是在重力异常中移去长波分量,对剩余部分进行拟合,并在拟合之后的解算点上恢复移去的长波分量。
利用EGM2008重力模型,能够得到该重力模型下实测点坐标处的重力异常值gEGMr和待测网格坐标处的重力异常值gEGM。首先计算gEGMr与实测点坐标处实际测量值gm的差值,即求得实测点坐标处重力异常残差值Δgresr:
| $ \Delta g_{{\rm{res}}}^r = {g_m}-g_{{\rm{EGM}}}^r $ | (1) |
这是移去-恢复法中“移去”的部分。
随后对Δgresr进行插值,得到待测网格点坐标处的重力异常值Δg′res,并将Δg′res与gEGM相加:
| $ {g_{{\rm{merge}}}} = \Delta g{\prime _{{\rm{res}}}} + {g_{{\rm{EGM}}}} $ | (2) |
这是移去-恢复法中“恢复”的部分,最终得到待测网格点坐标处的重力异常值gmerge。
对于该算法,本文从3个角度对其进行优化。
1.1 插值方法在缓冲区内部采用克里金插值,外部采用反距离权重插值。该方法的优点在于:在缓冲区内部,能够充分考虑测网的形状、大小及实测点的空间相互关系,对待测网格点进行线性无偏最优估计;在缓冲区外部,利用反距离权重法减少部分矩阵运算,较大程度上提高了插值效率。
1) 利用一系列实测点数据的相互位置关系h计算得到一系列变异函数γ(h),选取球状模型作为变异函数的理论模型进行γ(h)值拟合:
| $ \gamma \left( h \right) = \left\{ \begin{array}{l} 0, \;h = 0\\ {c_0} + c\left( {\frac{{3h}}{{2a}}-\frac{{{h^3}}}{{2{a^3}}}} \right), 0 < h \le a\\ {c_0} + c, h > a \end{array} \right. $ | (3) |
式中,c0为块金常数,c为拱高,a为变程。
2) 在待测网格点x周围有n个实测点数据,每个实测点的重力异常值为Z(xi), 则克里金插值公式为:
| $ {Z^*}\left( x \right) = \sum\limits_{i = 1}^n {{\lambda _i}Z({x_i})} $ | (4) |
式中,λi为权重系数,代表样本点对估计值的贡献量。
3) 克里金插值的实质是根据测量数据的空间分布特点和变异函数的结构特点对网格点区域化变量取值所进行的线性无偏和最优估计,即
| $ \left\{ \begin{array}{l} \sum\limits_{j = 1}^n {{\lambda _j}c} ({x_i}, {x_j})-\mu = c({x_i}, x)\\ \sum\limits_{i = 1}^n {{\lambda _i}} = 1 \end{array} \right. $ | (5) |
式中,μ为拉格朗日乘数。
4) 通过式(5)的求解可得克里格估计方差σE2,即
| $ {\sigma _E}^2 = c\left( {x, x} \right)-\sum\limits_{i = 1}^n {{\lambda _i}} c({x_i}, x) + \mu $ | (6) |
进而能够得到缓冲区内部待测网格点的重力异常更新值。
5) 在缓冲区外部采用反距离权重插值,分别计算待测网格点坐标与最邻近的一定数量实测点之间的距离,将距离的倒数看作权重,进而将一定数量的实测点重力异常值加权平均得到待测网格点处的重力异常值,即
| $ {Z^*}({x_0}) = \frac{{\sum\limits_{i = 1}^n {\frac{1}{{{{({D_i})}^p}}}} Z({x_i})}}{{\sum\limits_{i = 1}^n {\frac{1}{{{{({D_i})}^p}}}} }} $ | (7) |
反距离权重法主要思想为:实测点坐标与待测格网点坐标的距离越近,产生的影响就越大,插值计算时所赋权重也就越大。
1.2 考虑地形梯度考虑地形梯度因素,针对移去-恢复法的优化提出假设,即重力异常值与地形梯度存在相关性,地形梯度变化越大,重力异常值将发生越剧烈的改变。该异常改变主要是由地表附近地形起伏引起,而不是因为地球内部物质密度改变。基于此,地形梯度越大的坐标参与待测网格点插值时,其所赋权重应越小。
首先利用ASTER数字地形模型计算待测网格点的最大梯度值,通过数据预处理操作,得到待测网格点坐标处的最大梯度变量。步骤如下:
1) 通过归一化对地形梯度变量进行线性变化,将变量值映射到[0, 1]之间,消除变量量纲对结果的影响。变换函数为:
| $ x\prime = \frac{{x-{\rm{min}}}}{{{\rm{max-min}}}} $ | (8) |
2) 再通过标准化处理,使梯度变量满足均值E(x″) = 1,标准差σ(x″) = 1。E(x″) = 1能够将梯度变量当成权重变量,σ(x″) = 1确保不同类型的权重变量对插值结果的最终贡献相同。变换函数为:
| $ x" = \frac{{x'-\mu + 1}}{\sigma } $ | (9) |
我国的地震动态重力监测网主要分布在各个地震活动带上,早期的测网独立性高、关联性低,单个测网难以对整个区域进行有效控制。
根据测网空间分布,本文设计了划分更新范围的程序脚本,主要步骤为:
1) 根据测网的数量、形状和空间分布进行K-means分类,自动计算最优的分类数,保障各个区域测网的独立性。
2) 计算每个类别中测点的外包络线,并根据测网的精度确定缓冲区距离,计算缓冲区。
3) 根据前文的插值方法,在缓冲区内部利用实测点数据进行克里金插值,在缓冲区外部利用反距离权重法进行插值。
4) 若不同缓冲区存在交集部分,说明该区域在多个缓冲区内部,在对交集区域内的待测网格点插值时,综合利用缓冲区并集中各个实测点进行移去-恢复法插值计算。
通过CH指标来确定最佳分类数。该指标是通过定量描述类别内部离差矩阵的紧密度及类别间离差矩阵的分离度,计算得到最佳聚类结果。CH指标定义为:
| $ {\rm{CH}}\left( k \right) = \frac{{{\rm{tr}}\mathit{\boldsymbol{B}}\left( k \right)/\left( {k-1} \right)}}{{{\rm{tr}}\mathit{\boldsymbol{W}}\left( k \right)/\left( {n-k} \right)}} $ | (10) |
式中,n为聚类的总数目,k为当前的类别,trB (k)为类间离差矩阵的迹,trW (k)为类内离差矩阵的迹。
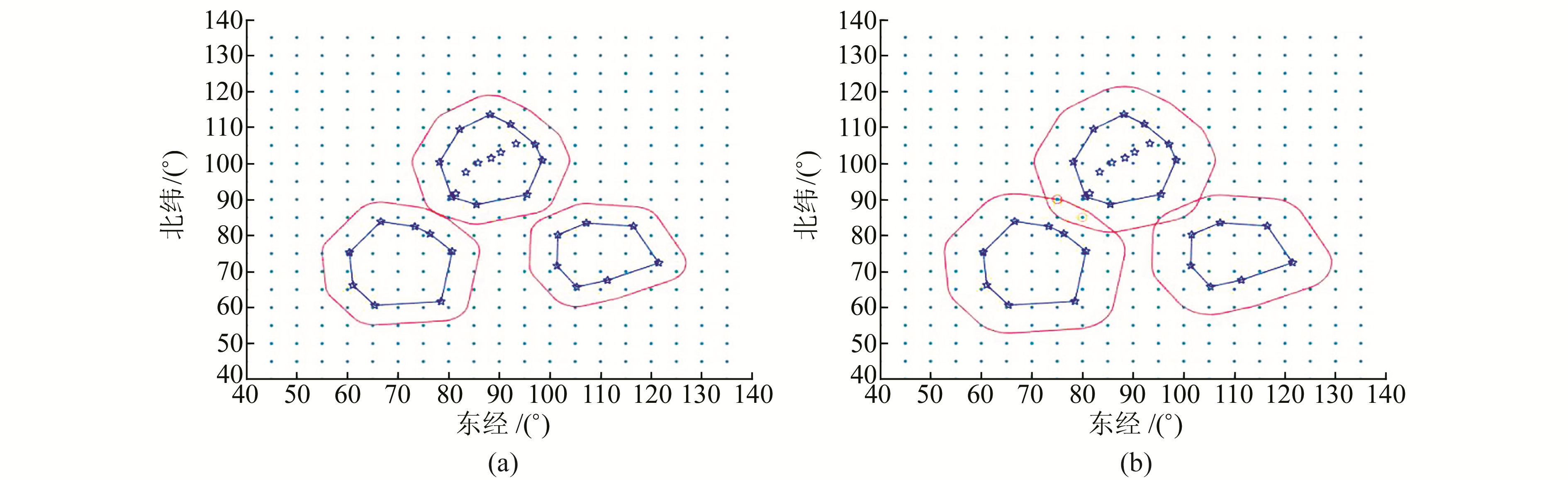
利用该脚本作出示意图,如图 1所示。其中,小圆点位置为待测网格点的地理坐标,五角星位置为实测点地理坐标,蓝线为测网的外包络线,红线为划定缓冲区距离后的整缓冲区范围,在其包围的范围内使用克里金插值法进行插值。图 1(b)将缓冲区距离扩大,当不同测网的缓冲区相交时,交集区域2个圆圈位置的待测网格点同时使用2个测网的实测数据进行插值。
|
图 1 改进移去-恢复法范围分析示意 Fig. 1 Range analysis example diagram |
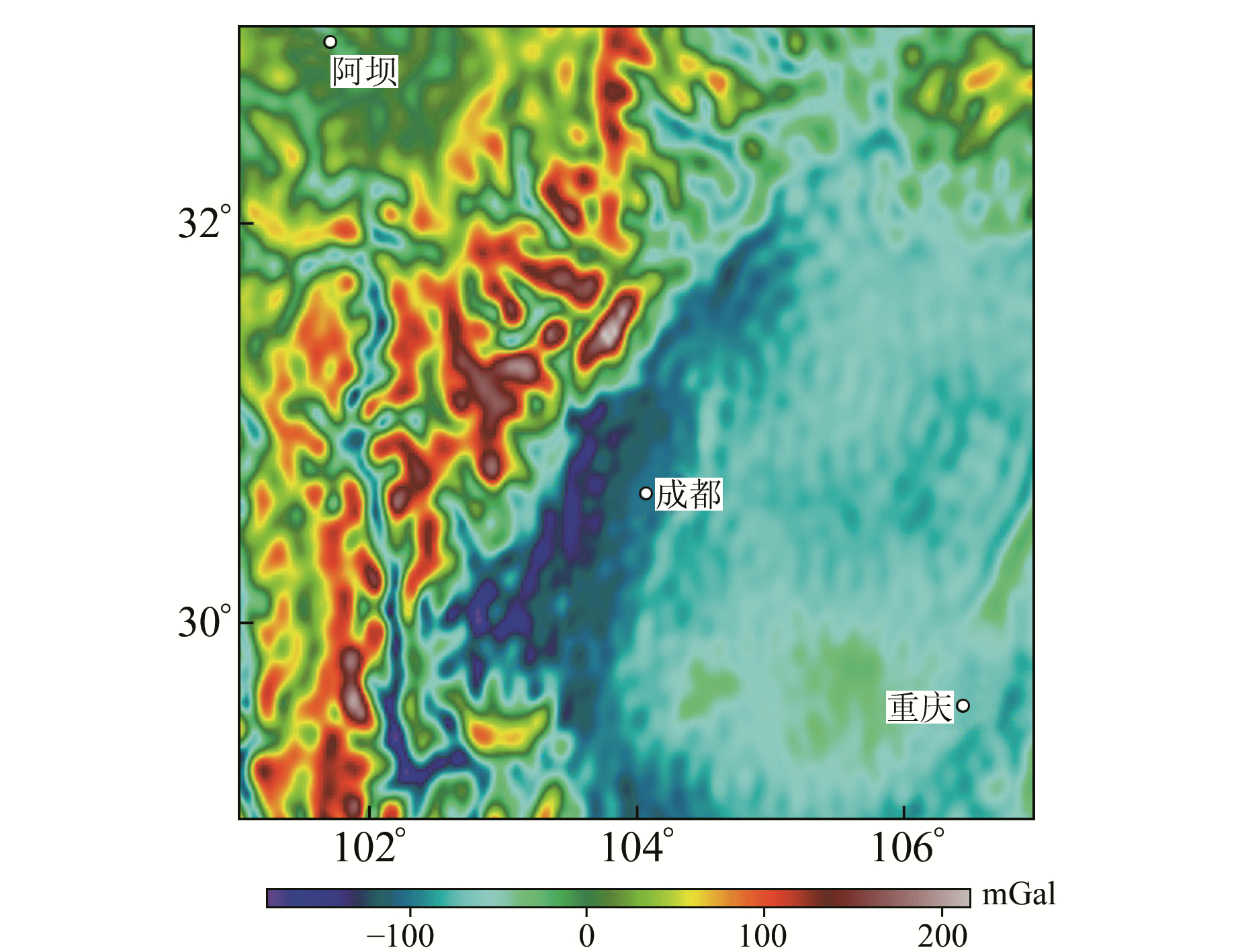
选取巴颜喀拉块体东缘的重力/GPS联合观测数据作为实测数据,在ICGEM的官方网站下载区域范围为29°~33°N、101°~107°E,网格分辨率为5″×5″的重力异常场数据。联合观测数据包括松潘-武胜测线、马尔康-内江测线、四川盆地测网、小金-雅安测线和康定-雅安测线,共计4条测线及1个测网[5-6]。计算结果如图 2所示。
|
图 2 川西地区自由空气重力异常图 Fig. 2 Free air gravity anomalous map in west Sichuan |
从图 2可以看出,优化后移去-恢复法插值有效平滑该地区重力场,较好地压制了地形起伏剧烈区的重力模型数据。通过计算利用不同方法平滑重力场模型后的标准差,能够直观地衡量利用移去-恢复法后该地区的插值效果(表 1)。
|
|
表 1 不同方法计算重力场模型标准差 Tab. 1 Different methods for calculating standard deviation of gravity field model |
表 1表明,经典的移去-恢复法能够较好地平滑重力场模型,标准差从65.09 mGal降至61.24 mGal。参考地形梯度因素,加入地形梯度变量后能进一步平滑重力场模型,使标准差降至59.31 mGal,有效印证了地形梯度因素在移去-恢复法中具有促进效果的假设。
3 喜马拉雅东构造结及邻区重力场校正喜马拉雅东构造结位于弧形山系东部弧顶区域,地处青藏高原、印度次大陆及缅甸三地交界处,地形和地质构造复杂,雅鲁藏布江、怒江、澜沧江等河流贯穿其中。其北部区域主要是海拔超过4 000 m的喜马拉雅山脉,地形起伏较为剧烈[7];南部为广阔的布拉马普特拉河谷地,地势平坦,海拔均在200 m以下。图 3中部区域为喜马拉雅山区南部的边缘地带,地势下降剧烈,海拔从4 000 m骤降至2 000 m左右。

|
图 3 喜马拉雅东构造结地形 Fig. 3 Eastern Himalayan syntaxis topographic map |
由于地形复杂,该地区广泛布控地面观测点难度较大,有将近一半的区域为重力空白区,目前仅有少量的地面观测点。对该区重力场研究的数据资料主要来源于EGM2008地球重力场模型,使用国际重力局提供的283个实测点重力异常数据,利用优化后的移去-恢复法计算该区自由空气重力异常(图 4)、布格重力异常(图 5)及均衡重力异常(图 6)。

|
图 4 喜马拉雅东构造结自由空气重力异常 Fig. 4 Eastern Himalayan syntaxis free air gravity anomaly map |
|
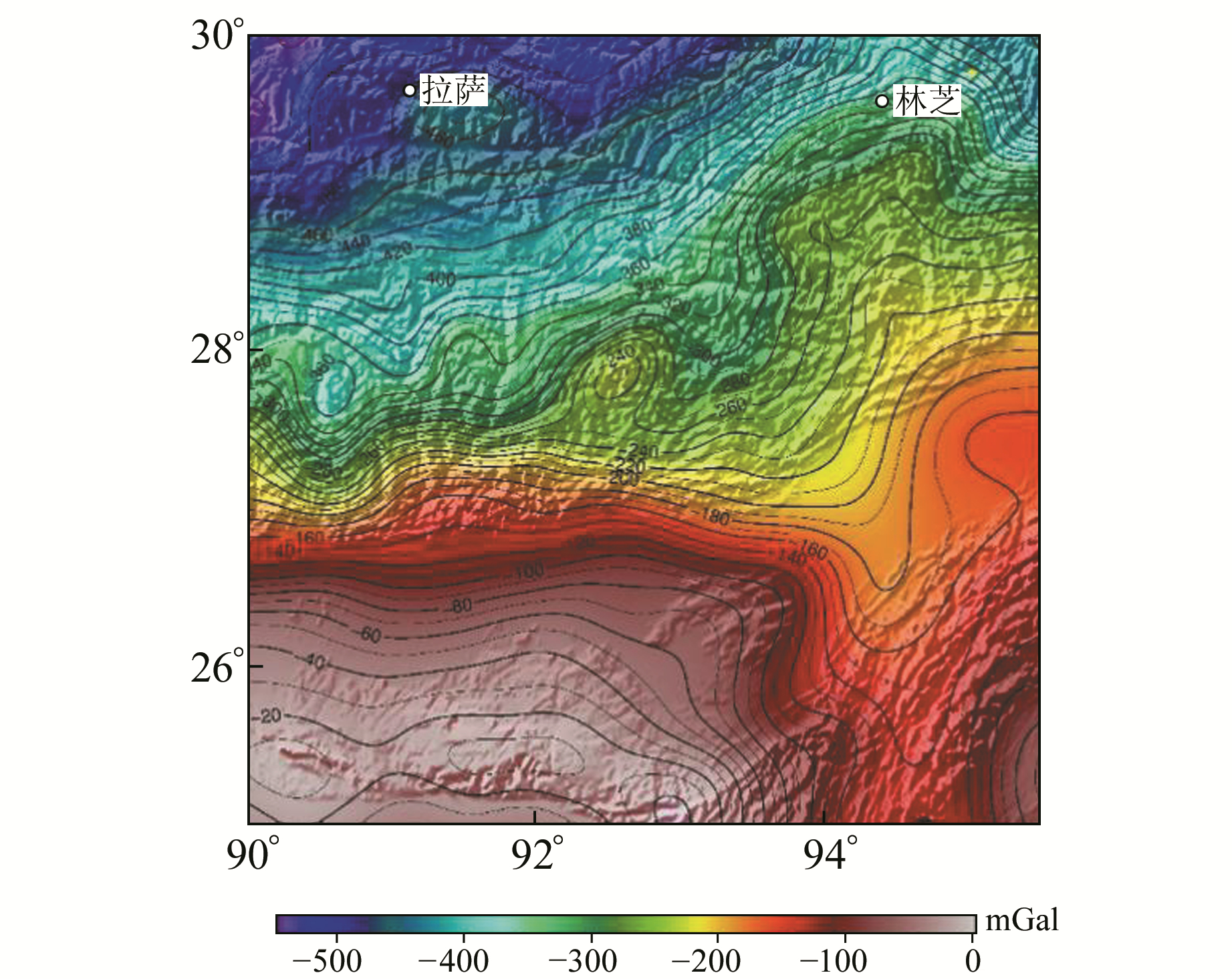
图 5 喜马拉雅东构造结布格重力异常 Fig. 5 Eastern Himalayan syntaxis Bouguer gravity anomaly map |

|
图 6 喜马拉雅东构造结均衡重力异常 Fig. 6 Eastern Himalayan syntaxis isostatic gravity anomaly map |
从图 4可以看出,研究区的自由空气重力异常值普遍在-80~250 mGal之间,个别区域低值达到-300 mGal,高值达到500 mGal。其中,中东部地区存在显著的大范围重力异常低值区,分布在-100~-200 mGal之间,形成原因与深层地质构造有关;西部区域重力异常值存在显著的纵向变化,以喜马拉雅山区南部边缘为界,界线以北的区域地势高,但地形较为平缓,自由空气重力异常值在-100~100 mGal之间,界线以南区域由于地势下降剧烈,范围内的空气异常值变化同样剧烈,存在较多的重力异常高值区,近三成区域的重力异常值超过200 mGal,同时交叉存在着很多重力异常低值点;中部谷地地势低缓,重力异常值分布均匀,在-150~0 mGal之间。通过移去-恢复法计算得到的自由空气重力异常,其图像特征与整个喜马拉雅山区及南部的地势构造特征高度吻合。
从图 5可以看出,研究区的布格重力异常值在-500~0 mGal之间,均值为-240 mGal左右。其空间分布主要表现为北部低、南部高,其中南部中段有明显低值带,部分地区异常值低于-150 mGal;西部区域的异常值在南北方向衰减较为剧烈,在27°~29°N范围内异常值从-150 mGal衰减至-500 mGal;西南部有较大面积的布格重力异常高值区,均值为-50 mGal左右。该区的布格重力异常空间分布有较强规律性,存在显著的南北纵向变化特征。
划分布格重力异常值的特征区为:北部边缘的布格重力异常极低值区为喜马拉雅山区,地势较高,海拔在4 000 m以上,布格重力异常值为-500 mGal左右;中北部为喜马拉雅山区南部边缘地带,海拔骤降至2 000 m左右,相应的布格重力异常值也随之升高至-160 mGal左右;西南部大片区域为谷地,海拔骤降至50 m左右,其布格重力异常值进一步升高至0~-100 mGal;东南部为那迦山山脉区域,由西向东布格重力异常值从-100 mGal降至-200 mGal,又升至-100 mGal;东北部林芝区域布格重力异常由北向南递增,东西部分布较为均匀。
由图 6可知,研究区的均衡重力异常分布范围较为广泛,在-140~120 mGal之间,全区有3个较为明显的均衡重力异常区域:1)北部为喜马拉雅山区南部边缘区域,其地势下降较为迅速,沿山区边缘分布有多个离散的均衡重力异常高值区,最大值达到120 mGal;2)南部为谷地边缘处,其地势由北向南开始变高,均衡重力异常值范围较大,最大达到80 mGal;3)中东部区域存在一个显著负均衡异常区,均衡重力异常值降至-150 mGal,其成因不仅与地壳均衡状态有关,还与该区的深部构造特征相关。
4 结语本文从多个角度对移去-恢复法进行优化,并结合川西地区的实测数据对优化方法的可行性进行验证,并利用该方法恢复并分析了喜马拉雅东构造结区域的重力异常场。
1) 移去-恢复法能够有效融合多元重力数据,利用少量的实测数据,更新较低精度的重力场,并能有效减弱高频信号的影响。通过对测网的空间位置分布进行分析,自动识别测网间的空间关系,并建立缓冲区,进而在不同区域内分别采用克里金插值和反距离权重插值法,在保证重点插值区域精度的同时,提高了插值效率。
2) 验证了地形梯度因素会对移去-恢复法产生影响的假设。地形梯度变化大,重力异常值通常也会发生较为剧烈的变化,其变化主要是由地表附近的地形起伏引起,而非地球深部物质密度改变造成,故地形梯度变化较大的区域参与待测网格点插值时所赋权重应该较小。利用川西实测数据证明,引入地形梯度变量能够更好地减小重力异常标准差,平滑重力异常场。
3) 通过对喜马拉雅东构造结及邻近地区进行计算分析发现,在喜马拉雅山区南缘地势下降剧烈的区域存在显著的自由空气重力异常高值区,且异常与地形有很好的契合;布格重力异常分布有较强的方向性,整体上呈现南高北低的特点;该区存在3个明显的均衡重力异常区,西部区域地势变化较为剧烈,有2个均衡高值区,而中东部地区存在显著的均衡重力异常低值区。
| [1] |
宁津生, 罗志才, 杨沾吉, 等. 深圳市1 km高分辨率厘米级高精度大地水准面的确定[J]. 测绘学报, 2003, 32(2): 102-107 (Ning Jinsheng, Luo Zhicai, Yang Zhanji, et al. Determination of Shenzhen Geoid with 1 km Resolution and Centimeter Accuracy[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(2): 102-107 DOI:10.3321/j.issn:1001-1595.2003.02.002)
(  0) 0) |
| [2] |
荣敏, 周巍, 陈春旺. 重力场模型EGM2008和EGM96在中国地区的比较与评价[J]. 大地测量与地球动力学, 2009, 29(6): 123-125 (Rong Min, Zhou Wei, Chen Chunwang. Evaluation of Gravity Field Models EGM2008 and EGM96 Applied in Chinese Area[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 123-125)
(  0) 0) |
| [3] |
陆彩萍, 伍吉仓, 王解先. 顾及EGM96模型的GPS水准高程拟合[J]. 测绘工程, 2002, 11(3): 31-34 (Lu Caiping, Wu Jicang, Wang Jiexian. The GPS/Lever Height Fitting Considering of EGM96[J]. Engineering of Surveying and Mapping, 2002, 11(3): 31-34 DOI:10.3969/j.issn.1006-7949.2002.03.009)
(  0) 0) |
| [4] |
管真, 陈剑杰, 尉伯虎, 等. 基于EGM2008的GPS水准拟合在复杂地形中的应用研究[J]. 大地测量与地球动力学, 2012, 32(4): 120-124 (Guan Zhen, Chen Jianjie, Yu Bohu, et al. Application of GPS Leveling Fitting Based on EGM2008 in Complex Terrain[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 120-124)
(  0) 0) |
| [5] |
付广裕, 祝意青, 高尚华, 等. 川西地区实测自由空气重力异常与EGM2008模型结果的差异[J]. 地球物理学报, 2013, 56(11): 3761-3769 (Fu Guangyu, Zhu Yiqing, Gao Shanghua, et al. Discrepancies between Free-Air Gravity Anomalies from EGM2008 and the Dense Gravity, GPS Observations at West Sichuan Basin[J]. Chinese Journal of Geophysics, 2013, 56(11): 3761-3769 DOI:10.6038/cjg20131117)
(  0) 0) |
| [6] |
佘雅文, 付广裕, 王灼华, 等. 重力与地形数据揭示的巴颜喀拉块体东缘垂向构造应力场[J]. 地球物理学报, 2017, 60(6): 2480-2492 (She Yawen, Fu Guangyu, Wang Zhuohua, et al. Vertical Tectonic Stress in Eastern Margin of Bayan Har Block Revealed by Gravity and Terrain Data[J]. Chinese Journal of Geophysics, 2017, 60(6): 2480-2492)
(  0) 0) |
| [7] |
滕吉文, 王谦身, 王光杰, 等. 喜马拉雅"东构造结"地区的特异重力场与深部地壳结构[J]. 地球物理学报, 2006, 49(4): 1045-1052 (Teng Jiwen, Wang Qianshen, Wang Guangjie, et al. Specific Gravity Field and Deep Crustal Structure of the 'Himalayas East Structural Knot'[J]. Chinese Journal of Geophysics, 2006, 49(4): 1045-1052 DOI:10.3321/j.issn:0001-5733.2006.04.016)
(  0) 0) |
2. Anhui Earthquake Agency, 558 West-Changjiang Road, Hefei 230031, China
 2019, Vol. 39
2019, Vol. 39

