2. 中国科学院大学, 北京市玉泉路19号甲, 100049
南海是西太平洋的边缘海盆之一,地处欧亚板块、菲律宾海板块和印度-澳大利亚板块的交汇地带,其形成和打开受特提斯构造域和太平洋构造域作用影响[1-2]。南海的形成和演化过程一直是地球科学的研究热点,不同地质历史时期的构造活动均会在岩石圈中留下痕迹,研究南海及邻区岩石圈结构特征对认识南海的形成和演化规律具有重要意义。近年来,随着地球物理数据的积累,已有多种反演南海莫霍面深度的成果陆续发表,前人在南海及邻区进行了声呐浮标探测[3]、双船扩展剖面探测[4]和海底地震仪探测剖面[5-10],并计算测量剖面上的莫霍面深度。Braitenberg等[11]考虑海洋岩石圈弹性形变,利用卫星重力数据计算南海海盆的莫霍面深度; 秦静欣等[12]利用空间重力异常数据,联合地形和地震剖面数据,通过三维带控制点界面反演算法,计算得到南海及邻区的莫霍面深度。由于采用的数据来源及计算方法不同,南海及邻区的莫霍面显示有不同的变化范围和深度特征。本文在前人研究基础上,采用EGM2008重力场模型联合GOCE卫星重力场模型,计算得到研究区内的高精度重力异常数据,进一步研究南海地区的重力场特征。同时联合海底地形、沉积层厚度及地震探测剖面等资料,计算南海及邻区的莫霍面深度,为综合解释南海及邻区地壳的构造属性和海盆的扩张机制提供依据。
1 数据来源及处理方法 1.1 数据来源本文研究范围为106°~120°E、8°~22°N。受研究区内地面/船测重力数据质量的限制,根据EGM2008重力场模型计算的自由空气重力异常的短波长精度有待提高[13-14]。研究发现,由GRACE和GOCE重力卫星观测数据解算得到的重力场模型,在波长小于100 km时的精度较高[14-15]。为提高研究区的重力场精度,本文将EGM2008重力场模型中的前200阶替换为GO_CONS_GCF_2_SPW_R2[15](基于GOCE重力卫星观测数据解算得到)的前200阶,替换后的位系数模型计算得到的重力异常为研究区域的自由空气重力异常。在计算过程中对数据进行UTM投影重采样为10 km×10 km的格网数据。
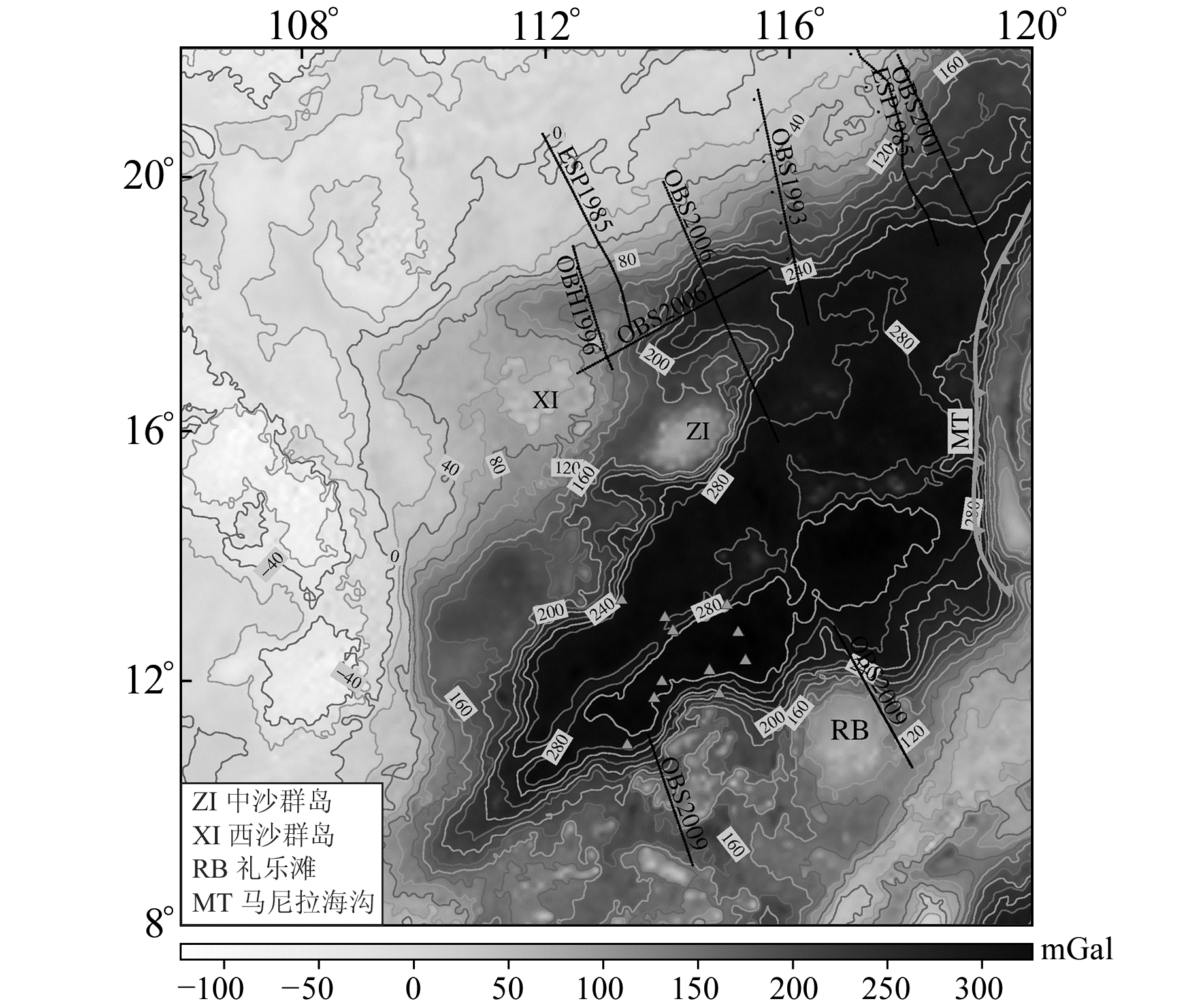
1.2 布格改正自由空气重力异常是地球内部物质密度分布不均匀性在地表的综合反映。在研究区内,自由空气重力异常可认为是海水、(新、中生代)沉积层、地壳、地幔岩石圈和岩石圈以下物质密度异常的总体响应。利用重力异常反演莫霍面深度,需要从观测重力异常中分离出莫霍面起伏所引起的重力异常。首先对自由空气重力异常数据采用完全布格校正的方法消除海底地形的影响,解算得到研究区的布格重力异常,地形数据采用GEBCO数据[16],校正密度为2 670 kg/m3[11-12]。研究区经过完全布格改正之后的布格重力异常见图 1。
|
图 1 研究区布格重力异常 Fig. 1 Bouguer gravity anomaly in the study region |
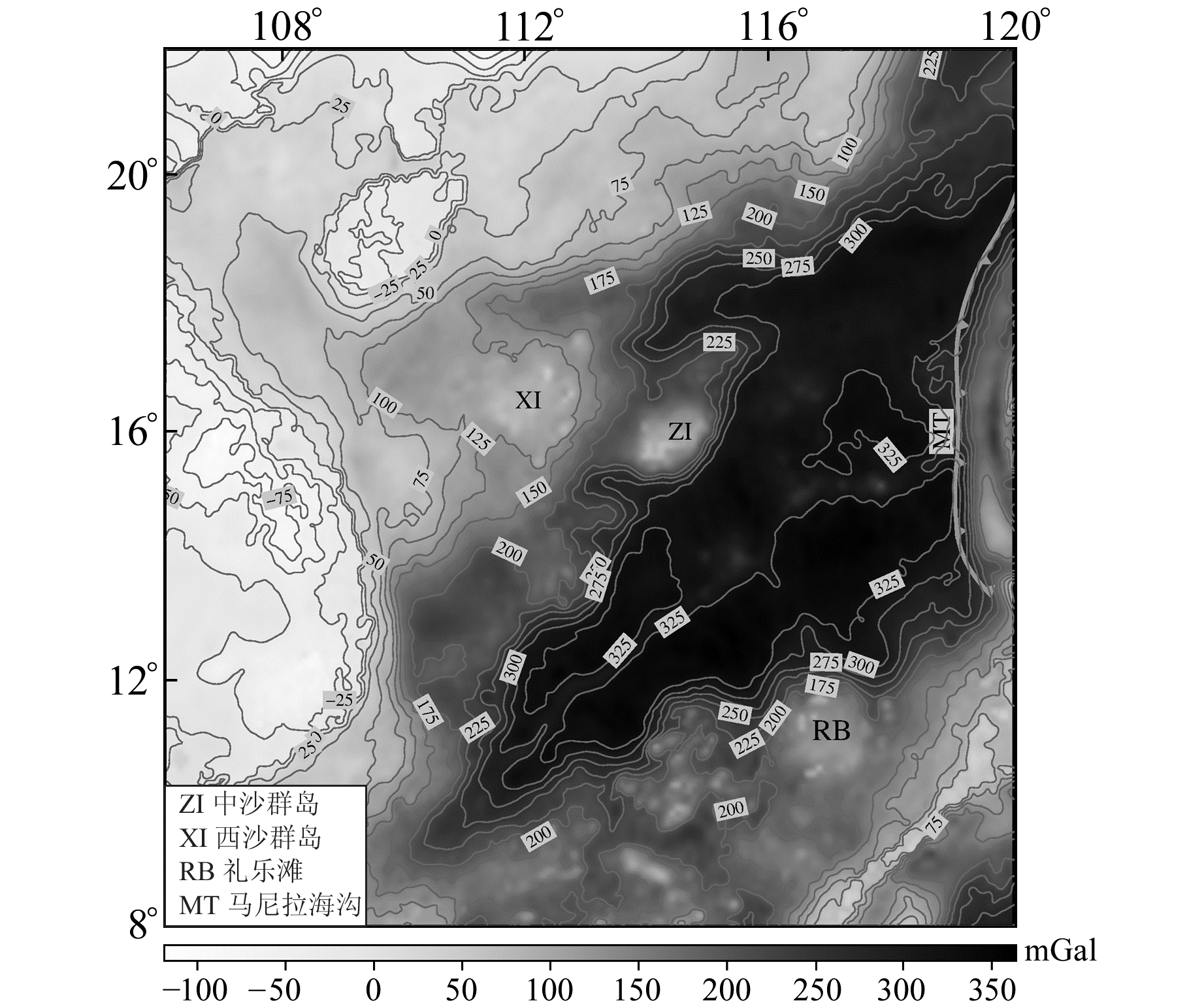
相关研究表明[11],南海海盆及邻区基底覆盖有0.5~12 km厚度不等的新、中生代沉积层。由于基底上、下界面密度差在有些区域可达300 kg/m3,沉积层内部同样存在密度分布不均匀的异常体,因此重力场分离时有必要在观测重力异常中扣除由沉积层内密度异常引起的重力异常。沉积层厚度采用美国NOAA公布的分辨率为5′×5′的格网数据[17],密度分布(ρz)采用指数密度[18]分布模型拟合,拟合公式为ρz = Φ0e-czρw+(1-Φ0e-cz)ρsg,其中, Φ0为初始沉积物孔隙度,z为沉积层厚度,c为转换参数,ρw为海水密度,取值1 030 kg/m3,ρsg为填充颗粒物密度。Φ0、c、ρsg的取值根据研究区内海底地震仪探测剖面的P波波速,通过波速-密度转换关系[19]计算得到:Φ0 = 0.54, c = 4.75×10-4m-1, ρsg = 2 650 kg/m3,自由空气重力异常通过地形改正和沉积层密度异常改正后的剩余重力异常见图 2。
|
图 2 重力场分离得到的莫霍面起伏的剩余重力异常 Fig. 2 Residual gravity anomaly used to calculate Moho depths |
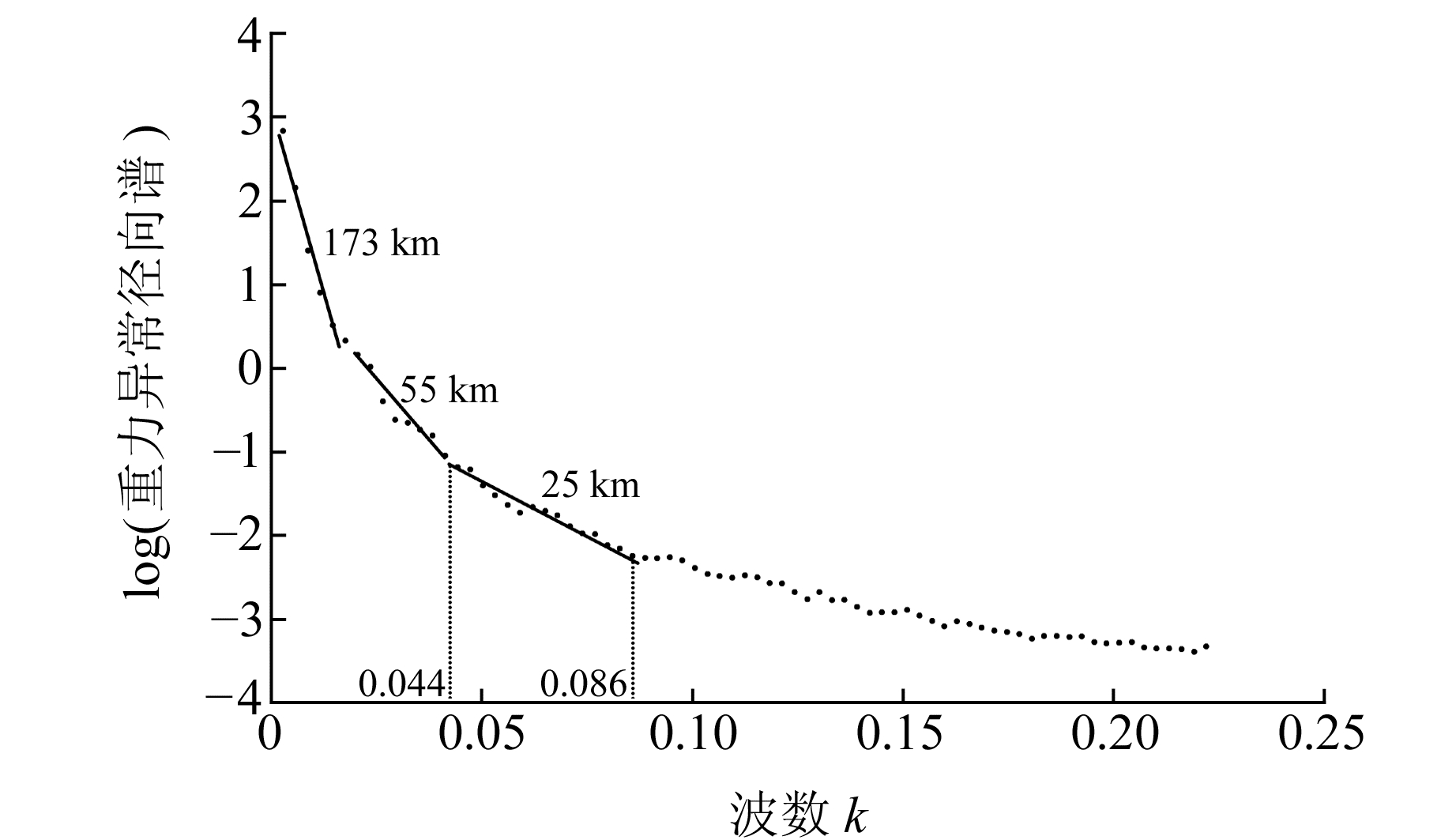
地壳的密度异常引起的重力异常一般被认为是高频异常,布格异常扣除中、新生代沉积层密度异常引起的重力异常之后,得到的剩余异常主要包含莫霍面起伏引起的重力异常及地幔岩石圈和岩石圈以下物质密度异常引起的重力异常,通过解算该剩余异常的对数振幅谱与波数的对应关系(图 3),分离出莫霍面起伏引起的重力异常。根据前人研究成果[11-12]和海底地震仪探测剖面[3-10]的结果,研究区域莫霍面深度约在7~40 km,图 3显示的25 km对应研究区的平均莫霍面深度。图 3中另外可见平均深度为173 km和55 km的异常波段,平均深度173 km的波段对应地幔岩石圈以下密度异常引起的重力异常,主要是长波长异常。由于南海海盆是新生代大陆破裂、海底扩张形成的边缘海盆,在距今约15.5 Ma时停止扩张[1-2],而大陆破裂、海底扩张形成的非稳态的温度场环境引起的岩石圈内的密度异常,是产生平均深度为55 km重力异常波段的主要原因。对于平均深度为173 km和55 km对应的重力异常项,主要采用滤波器(式(3))来扣除。
|
图 3 剩余重力异常对数振幅谱与波数的关系 Fig. 3 The plot of the logarithm of the power in the Bouguer gravity spectrum as a function of wavenumber |
为控制反演过程中的参数,同时评价反演质量,本文搜集在研究区内的声呐浮标探测[3]、双船扩展剖面探测[4]和海底地震仪探测剖面[5-10],计算得到71个莫霍面深度资料作为反演质量的检核点,检核点的位置分布见图 1。
2 Parker-Oldenburg反演算法及参数设置Parker [20]提出频率域内计算起伏界面重力异常的公式,Oldenburg[21]在Parker公式的基础上,将正演公式变为迭代反演形式,提出单界面模式的位场迭代反演公式,即
| $ F[\Delta g] = - 2{\rm{ \mathsf{ π} }}G\rho {{\rm{e}}^{ - k{z_0}}}\sum\limits_{n = 1}^\infty {\frac{{{k^{n - 1}}}}{{n!}}} F[{h^n}\left( {\left( {\vec r} \right)} \right] $ | (1) |
| $ F\left[{h\left( {\vec r} \right)} \right] = - \frac{{{\rm{ }}F[\Delta g]}}{{2{\rm{ \mathsf{ π} }}G\rho }}{{\rm{e}}^{k{z_0}}} - \sum\limits_{n = 2}^\infty {\frac{{{k^{n - 1}}}}{{n!}}F[{h^n}\left( {\left( {\vec r} \right)} \right]} {\rm{ }} $ | (2) |
式中,Δg为观测重力异常,h(
根据式(1)和(2),利用上文数据处理得到的剩余重力异常进行反演,计算南海及邻区的莫霍面深度。在计算过程中,为适应研究区地质构造环境,式(2)中的高频放大因子ekz0、观测平面z0、密度差ρ和迭代的收敛条件需要相关的参数设置。
由于式(2)中的ekz0会使重力场的高频噪声放大,影响反演过程的收敛性,本文采用Oldenburg[21]定义的低通滤波器HCF(k)来控制高频噪声。滤波器表达式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{HCK}}\left( k \right) = \\ \left\{ \begin{array}{l} 1, k/2{\rm{ \mathsf{ π} }} < {\rm{WH}}\\ \frac{1}{2}[1 + {\rm{cos}}(\frac{{k-2{\rm{ \mathsf{ π} WH}}}}{{2({\rm{SH-WH}})}})], {\rm{WH}} \le (k/2{\rm{ \mathsf{ π} }}) \le {\rm{SH}}\\ 0, k/2{\rm{ \mathsf{ π} }} > {\rm{SH}} \end{array} \right. \end{array} $ | (3) |
式中,k为波数,WH和SH为滤波参数,通过重力异常的对数振幅谱估计(图 3)。由图 3可以看出,研究区内的平均莫霍面深度为25 km,即式(2)中z0 = 25 km,对应的波长范围为70~151 km,对应的高通和低通滤波参数分别为SH = 0.014 2和WH = 0.006 6。
通过对研究区OBS剖面提供的地震波速度计算发现,研究区莫霍面的密度差数值估计在300~550 kg/m3。本文采用迭代计算来获取研究区最佳的密度差ρ,具体计算过程则是通过设定密度差300~550 kg/m3以10 kg/m3的间隔变化,将不同密度差计算的莫霍面深度结果与地震剖面控制点的结果作差,均方根误差最小的一组对应的密度差ρ即为研究区内采用的最终密度差。通过26次反演计算,ρ = 420 kg/m3对应的均方根误差最小,为1.9 km。
迭代的收敛性控制则根据
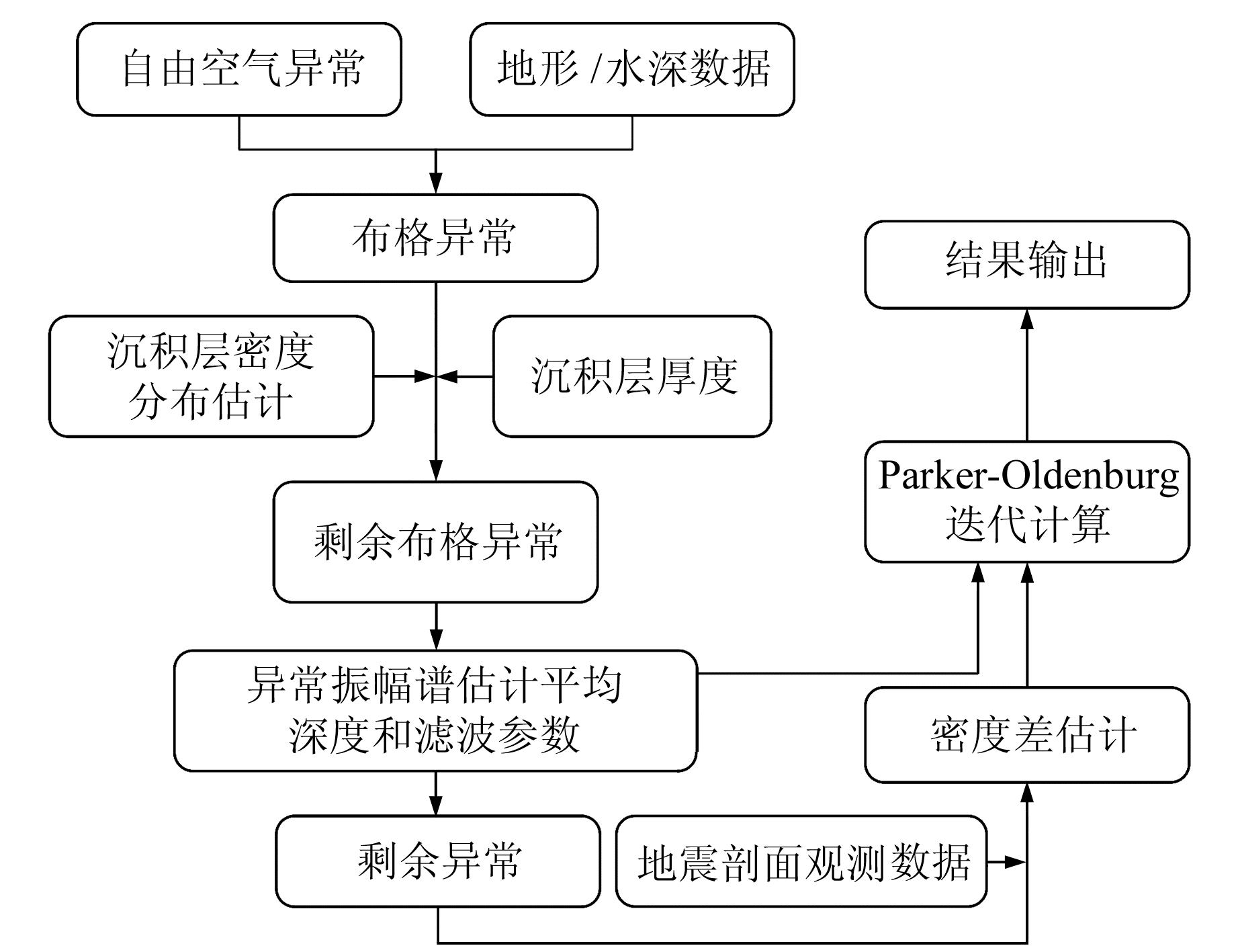
|
图 4 利用重力异常数据计算研究区内莫霍面深度分布流程 Fig. 4 Flowchart of illustrating the inversion of the Moho depths |
本文搜集的地震剖面控制点共71个,地震观测数据结果的误差为±2 km[3-5],反演结果与控制点观测结果的平均偏差为1.59 km,标准偏差为1.9 km。经统计分析,71个控制点中有86%的点差值在±2 km以内,反演结果比较可靠。计算得到的莫霍面深度分布见图 5。

|
图 5 重力异常反演计算得到的莫霍面深度分布 Fig. 5 Moho depths calculated from gravity anomaly |
与前人[12,22-23]得到的莫霍面深度结果相比,图 5显示的莫霍面在海区的深度有所不同。海盆区莫霍面深度约为8.0~13.0 km,与前人的计算结果约差0.5~1 km;在海盆北部洋陆过渡区,莫霍面深度与前人计算结果约差1~2 km。本文采用基于GOCE重力卫星观测数据解算得到的重力场模型GO_CONS_GCF_2_SPW_R2的前200阶替换EGM2008重力场模型的前200阶,提高了输入数据的重力异常精度。对比采用测高重力异常得到的莫霍面深度结果,测高卫星计算的莫霍面深度与地震剖面控制点计算结果的平均差值为1.67 km,替换后的重力异常使计算结果的可靠性略有提高。根据南海地质特征分离各层重力异常,尤其在扣除沉积层的重力异常时,采用指数形式的变密度公式拟合密度异常,提高剩余重力异常的精度。海盆区由于沉积层厚度较小,莫霍面深度与前人的计算结果差值小于1 km,而在沉积层厚度较大的区域,如莺歌海盆地,沉积层最大厚度大于13 km[11,24],莫霍面深度与前人结果相差1.5~3 km。但本文计算的莫霍面深度与海底地震仪探测OBH1996剖面[24]计算得到的莫霍面深度更为相符,对比前人采用常数密度拟合沉积层密度异常的计算结果,变密度沉积层模型的拟合结果更为可靠。
图 5显示,研究区的莫霍面深度分布具有明显的区域化特征,莫霍面起伏较大,显示为经历复杂地质构造活动形成的边缘海盆地壳结构特征。若以莫霍面深度和地壳厚度作为划分陆壳、洋陆过渡性地壳和洋壳的依据,图 5反映出南海及邻区同时具有这3种类型的地壳,这与前人的研究结果一致。陆地区华南大陆和中印半岛莫霍面深度大于25 km,地壳厚度大于20 km,属于陆壳;西沙群岛、中沙群岛地区莫霍面深度表现为同心圆状隆升,地壳厚度大于20 km,属于陆壳;洋陆过渡壳主要分布在水深为0~3 000 m的区域,地壳厚度小于20 km,莫霍面深度约为13~25 km,莫霍面水平变化梯度大,等值线密集;海盆东侧边缘为马尼拉海沟俯冲带,莫霍面剧烈俯冲,莫霍面深度约为8.0~13.0 km,地壳厚度约为5.0~10.0 km,为洋壳。全区莫霍面深度最小处在西南次海盆,为8.0 km左右。图 5所示的莫霍面深度分布显示研究区内具有明显的海盆、海沟、岛弧等区域化构造特征。
4 结语本文利用Parker-Oldenburg频率域反演算法,采用重力异常数据反演计算南海及邻区的莫霍面深度分布。采用EGM2008全球重力场模型联合GOCE重力场模型,计算研究区的自由空气重力异常,通过对自由空气重力异常进行布格改正,获取研究区的布格重力异常。在布格重力异常中扣除由沉积层密度异常、地壳内密度异常和地幔岩石圈及岩石圈以下密度异常引起的重力异常后,得到研究区的剩余重力异常,利用剩余重力异常反演南海及邻区的莫霍面深度。采用低通滤波器控制反演算法的收敛性,滤波器截止频率通过计算重力异常对数振幅谱估计。搜集研究区地震剖面计算的莫霍面深度数据来控制反演参数,同时评价反演质量,计算结果与研究区内地震波探测剖面的莫霍面深度平均偏差为1.59 km,标准偏差为1.9 km。结果显示,海盆区莫霍面深度分布约为8.0~13.0 km,陆地区莫霍面深度大于25 km,陆地区与海盆区之间存在洋陆过渡型地壳,莫霍面起伏较大,研究区内的莫霍面深度分布具有明显的区域化特征。
| [1] |
Hall R. Cenozoic Geological and Plate Tectonic Evolution of SE Asia and the SW Pacific: Computer-Based Reconstructions, Model and Animations[J]. Journal of Asian Earth Sciences, 2002, 20(4): 353-431 DOI:10.1016/S1367-9120(01)00069-4
(  0) 0) |
| [2] |
Taylor B, Hayes D E. Origin and History of the South China Sea Basin[A]//Hayes D E.The Tectonic and Geologic Evolution of Southeast Asian Seas and Islands: Part 2[M]. Washington D C: American Geophysical Union (Geophysical Monograph), 1983
(  0) 0) |
| [3] |
Ludwig W J, Kumar N, Houtz R E. Profiler-Sonobuoy Measurements in the South China Sea Basin[J]. Journal of Geophysical Research:Solid Earth, 1979, 84(B7): 3505-3518 DOI:10.1029/JB084iB07p03505
(  0) 0) |
| [4] |
Nissen S S, Hayes D E, Buhl P, et al. Deep Penetration Seismic Soundings across the Northern Margin of the South China Sea[J]. Journal of Geophysical Research:Solid Earth, 1995, 100(B11): 22433
(  0) 0) |
| [5] |
Yan P, Zhou D, Liu Z S. A Crustal Structure Profile Accross the Northern Continental Margin of the South China Sea[J]. Tectonophysics, 2001, 338(1): 1-21 DOI:10.1016/S0040-1951(01)00062-2
(  0) 0) |
| [6] |
Hayes D E, Nissen S S. The South China Sea Margins: Implications for Rifting Contrasts[J]. Earth & Planetary Science Letters, 2005, 237(3): 601-616
(  0) 0) |
| [7] |
Wu Z L, Li J B, Ruan A G, et al. Crustal Structure of the Northwestern Sub-Basin, South China Sea: Results from a Wide-Angle Seismic Experiment[J]. Science China Earth Sciences, 2012, 55(1): 159-172 DOI:10.1007/s11430-011-4324-9
(  0) 0) |
| [8] |
Qiu X L, Ye S Y, Wu S M, et al. Crustal Structure across the Xisha Trough, Northwestern South China Sea[J]. Tectonophysics, 2001, 341(1): 179-193
(  0) 0) |
| [9] |
Wang T K, Chen M K, Lee C S, et al. Seismic Imaging of the Transitional Crust across the Northeastern Margin of the South China Sea[J]. Tectonophysics, 2006, 412(3): 237-254
(  0) 0) |
| [10] |
阮爱国, 牛雄伟, 丘学林, 等. 穿越南沙礼乐滩的海底地震仪广角地震试验[J]. 地球物理学报, 2011, 54(12): 3139-3149 (Ruan Aiguo, Niu Xiongwei, Qiu Xuelin, et al. A Wide Angle Ocean Bottom Seismometer Profile across Liyue Bank, the Southern Margin of South China Sea[J]. Chinese Journal of Geophysics, 2011, 54(12): 3139-3149 DOI:10.3969/j.issn.0001-5733.2011.12.014)
(  0) 0) |
| [11] |
Braitenberg C, Wienecke S, Wang Y. Basement Structures from Satellite-Derived Gravity Field: South China Sea Ridge[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B5)
(  0) 0) |
| [12] |
秦静欣, 郝天珧, 徐亚, 等. 南海及邻区莫霍面深度分布特征及其与各构造单元的关系[J]. 地球物理学报, 2011, 54(12): 3171-3183 (Qin Jingxin, Hao Tiantao, Xu Ya, et al. The Distribution Characteristics and the Relationship between the Tectonic Units of the Moho Depth in South China Sea and Adjacent Areas[J]. Chinese Journal of Geophysics, 2011, 54(12): 3171-3183 DOI:10.3969/j.issn.0001-5733.2011.12.017)
(  0) 0) |
| [13] |
Pavlis N K, Holmes S A, Kenyou S C, et al. Correction to "The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008)"[J]. Journal of Geophysical Research:Solid Earth, 2013, 118(5): 2633 DOI:10.1002/jgrb.50167
(  0) 0) |
| [14] |
Prasanna H M I, Chen W, Íz H B. High Resolution Local Moho Determination Using Gravity Inversion: A Case Study in Sri Lanka[J]. Journal of Asian Earth Sciences, 2013, 74(18): 62-70
(  0) 0) |
| [15] |
Migliaccio F, Reguzzoni M, Sansò F, et al. GOCE Data Analysis: The Space-Wise Approach and the First Space-Wise Gravity Field Model[C]. The ESA Living Planet Symposium, Lacoste, 2010
(  0) 0) |
| [16] |
IOC, IHO, BODC. Centenary Edition of the GEBCO Digital Atlas[Z]. Livepool, UK, 2003
(  0) 0) |
| [17] |
Whittaker J M, Goncharov A, Williams S E, et al. Global Sediment Thickness Data Set Updated for the Australian-Antarctic Southern Ocean[J]. Geochemistry Geophysics Geosystems, 2013, 14(8): 3297-3305 DOI:10.1002/ggge.20181
(  0) 0) |
| [18] |
Sawyer D S. Total Tectonic Subsidence: A Parameter for Distinguishing Crust Type at the US Atlantic Continental Margin[J]. Journal of Geophysical Research:Solid Earth, 1985, 90(B9): 7751-7769 DOI:10.1029/JB090iB09p07751
(  0) 0) |
| [19] |
Barton P J. The Relationship between Seismic Velocity and Density in the Continental Crust——A Useful Constraint?[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 87(1): 195-208
(  0) 0) |
| [20] |
Parker R L. The Rapid Calculation of Potential Anomalies[J]. Geophysical Journal International, 1973, 31(4): 447-455 DOI:10.1111/j.1365-246X.1973.tb06513.x
(  0) 0) |
| [21] |
Oldenburg D W. The Inversion and Interpretation of Gravity Anomalies[J]. Geophysics, 1974, 39(4): 526-536 DOI:10.1190/1.1440444
(  0) 0) |
| [22] |
刘光鼎. 中国海区及邻域地质地球物理系列图集[M]. 北京: 科学出版社, 1992 (Liu Guangding. Geophysical Series Maps in China Sea and Adjacent Regions[M]. Beijing: Science Press, 1992)
(  0) 0) |
| [23] |
Bai Y L, Williams S E, Müller R D, et al. Mapping Crustal Thickness Using Marine Gravity Data: Methods and Uncertainties[J]. Geophysics, 2014, 79(2): 1-10
(  0) 0) |
| [24] |
刘赛君, 曾钢平, 邱学林, 等. 海南岛西南海域地壳剖面海陆联合探测研究[J]. 地球物理学进展, 2011, 26(3): 922-933 (Liu Saijun, Zeng Gangping, Qiu Xuelin, et al. The Crustal Profile and Onshore-Offshore Seismic Exploration in the Marine Area Southwest to Hainan Island[J]. Progress in Geophys, 2011, 26(3): 922-933 DOI:10.3969/j.issn.1004-2903.2011.03.018)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39

