2. 中国地震局地壳应力研究所武汉创新基地,武汉市洪山侧路40号,430071
在许多M≥6.0地震前,均能观测到显著的重力场异常变化[1-3],在空间分布上往往表现为梯度带或四象限。目前,利用重力观测进行地震预测仍处于震例经验总结阶段,如何利用这些典型特征构建物理预测模型进行定量化预测,是地震数值预报发展面临的关键问题。孕震物理模型是定量化的前提,目前已有许多基于重力变化的定性孕震模式。申重阳等[4-5]从地壳运动的角度分析认为,震前重力变化为地壳内部密度变化和地壳形变耦合的一种结果,并提出用于解释四象限型重力前兆变化的“闭锁剪力模式”。本文根据姚安MS6.0地震震前典型重力场变化,基于闭锁剪力模式,探索定量化的孕震模型。
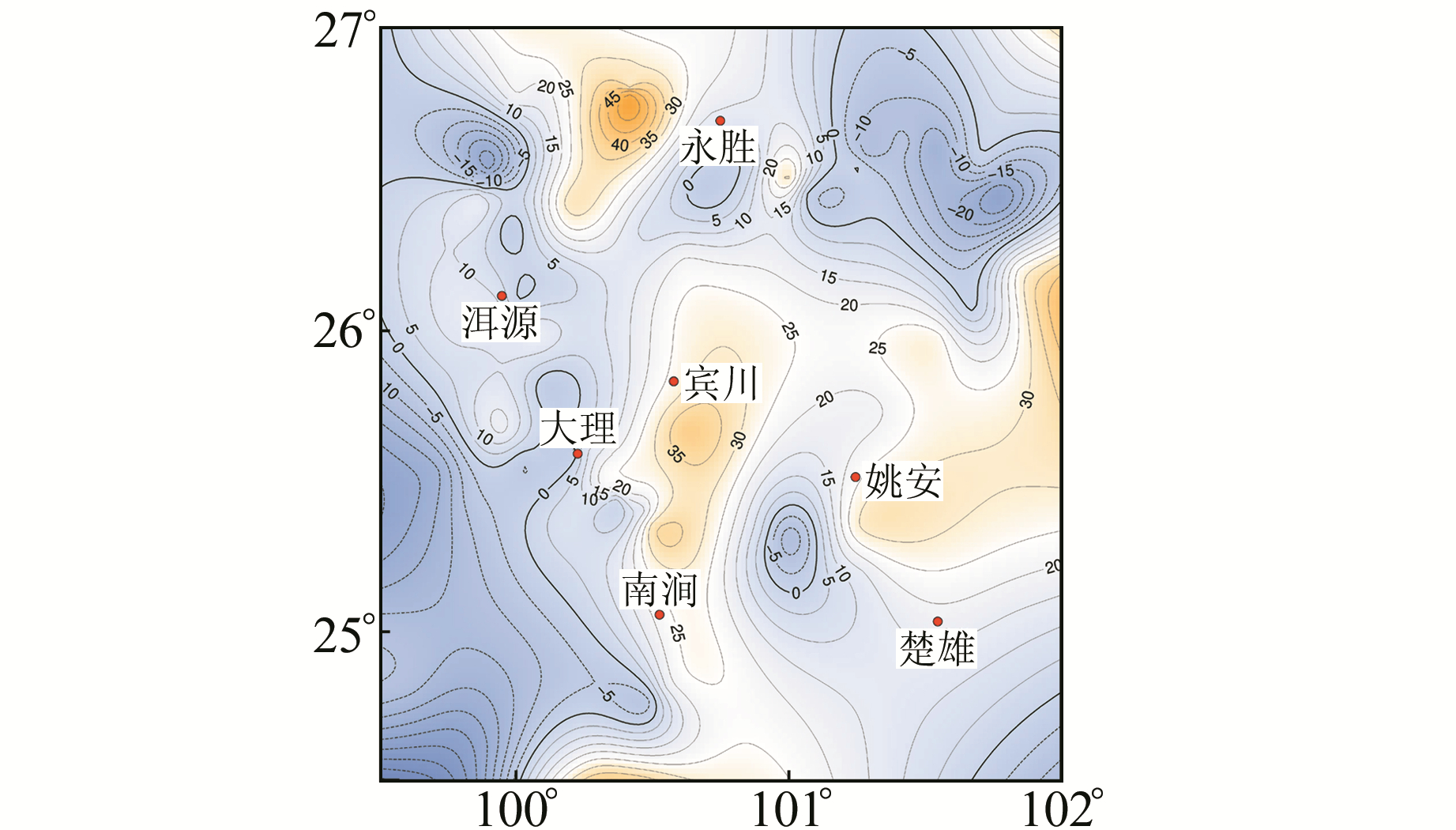
1 姚安地震典型重力前兆——问题提出2009-07-09云南省姚安县发生MS6.0地震,震中(25.6°N, 101.03°E)位于川滇块体南部,属于滇西地震实验场,是我国强震活动的重点监测区。1985年以来,该区域使用LCR-G型重力仪进行了每年不少于2期的高精度流动重力重复观测[6],并在姚安MS6.0地震前观测到震区重力场存在一定程度的变化。实践证明,震前3~4 a的重力资料反映了地震孕育的过程。申重阳等[5]通过分析该区域2005~2009年的重力动态差分变化认为,2008-10~2009-02姚安附近出现的重力变化四象限现象(图 1)与孕震过程有密切的联系,并据此提出闭锁剪力模式。本文选取2008-10~2009-02姚安MS6.0地震震中附近1.5°×1.5°范围内的重力变化图像为典型重力前兆,为突出图中的四象限变化异常,去除了与孕震过程无关的平均背景场变化(图 2)。
|
图 1 滇西网2008-10~2009-02重力场差分动态变化 Fig. 1 Difference dynamic gravity changes of west Yunnan region from October 2008 to February 2009 |
|
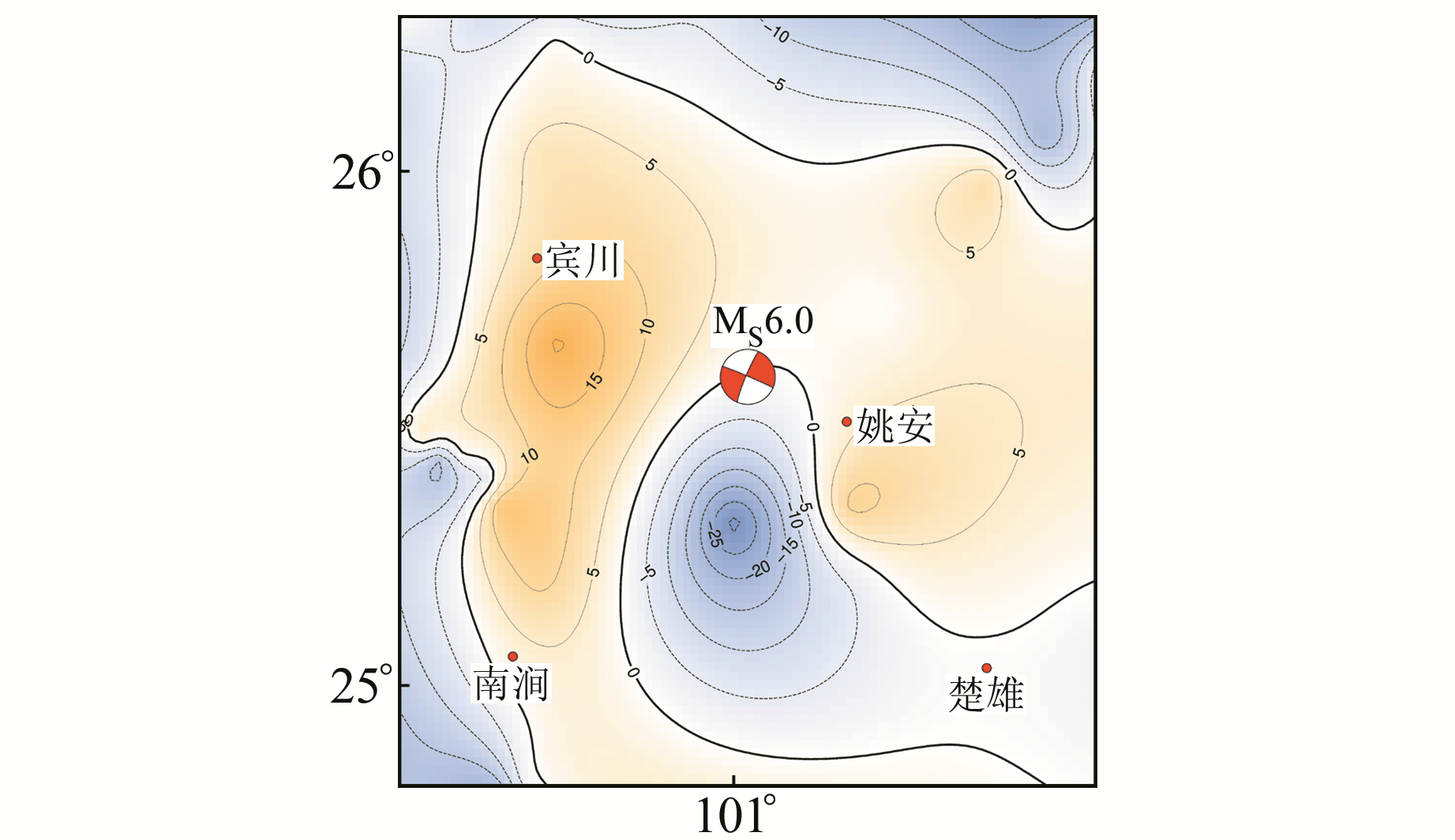
图 2 标准化处理后的姚安地区差分重力变化图像及震源机制解 Fig. 2 The normalizing difference gravity changes of Yao'an region and the focal mechanism solution |
图 2中姚安MS6.0地震的震源机制解数据来自GCMT。可以发现,姚安MS6.0地震震中位于重力差分变化零值线附近,同时也是重力异常变化高值与低值区形成的四象限中心。从图 2可看出,在震源机制解压缩区(红色)对应的象限震前重力呈现正变化,拉张区(白色)对应的象限震前重力呈现负变化。这种震前重力变化四象限所蕴含的“剪力”与地震发生时震源机制所反映的双力偶“剪力”的一致性,预示地震孕育过程中“先存剪力”的存在,即可认为震前存在的“闭锁剪力”与引发地震的剪应力在数学物理上有相似的表达。因此,如何基于闭锁剪力模式建立地表观测重力变化与孕震“剪力”之间的数学物理定量化模型是本文研究的重点,亦是检验该模式应用潜力的关键。
2 闭锁剪力模式的定量化模型闭锁剪力模式[5]假设地震孕育发生过程中孕震体自始至终存在双力偶“剪力”,“剪力”的生长决定了地震是否发展和发生。震前“剪力”尚不足以引起地震发生,称之为“闭锁剪力”;“闭锁剪力”达到一定程度,突破岩石极限而造成位错,释放能量。因此,可借用定量地震学震源理论,构建地震孕育发生统一的“剪力”模型。
根据定量地震学[7]观点,构造型地震是由剪切应力引起的体积崩溃。地震震源可以用跨越一个内表面两侧的位移间断来表示,Maruyama[8]证明位移间断可等效为一个双力偶体力fp,对于Σ上的一般位移间断,其等效体力为:
| $ {f_p}\left( {\eta, \tau } \right) = \mu \left[{u\left( {\eta, \tau } \right)} \right]\frac{\partial }{{\partial \eta }}\delta \left( \mathit{\Sigma } \right) $ | (1) |
式中,δ(Σ)表示在Σ以外为零的一维空间狄拉克δ函数。假设式(1)同样适用于孕震体,此时fp为闭锁剪力大小,u为等效位移间断,Σ视为潜在破裂面,双力偶“剪力”与“位错”具有等效性。
fp的力矩为:
| $ M = \mu UA $ | (2) |
在同震位错中,M为地震矩,用来表示地震所释放出的能量。对于闭锁剪力fp,M可称作孕震矩,用来表示地震孕育时震源积累的“能量”。式(2)中,μ为刚度,U为等效位移间断,A为潜在间断面(对应等效位移间断)的面积。式(1)和(2)的意义在于,可借鉴弹性剪切位错源与双力偶点源的数学等价性,用一个位错源来描述闭锁剪力,“闭锁剪力”引发的震前重力变化亦视作由该位错源产生。借鉴地震位错理论中位错与重力变化之间的数学解析关系,构建“闭锁剪力”的定量化模型,通过震前重力变化获取孕震矩,预测发震强度。这样可将“同震位错”有关理论推广到孕震情形,即可直接借用Okubo[9]的同震位错引起的重力变化理论,构建“等效位错”与地表重力变化的关系,间接建立“闭锁剪力”与地表重力变化的关系。
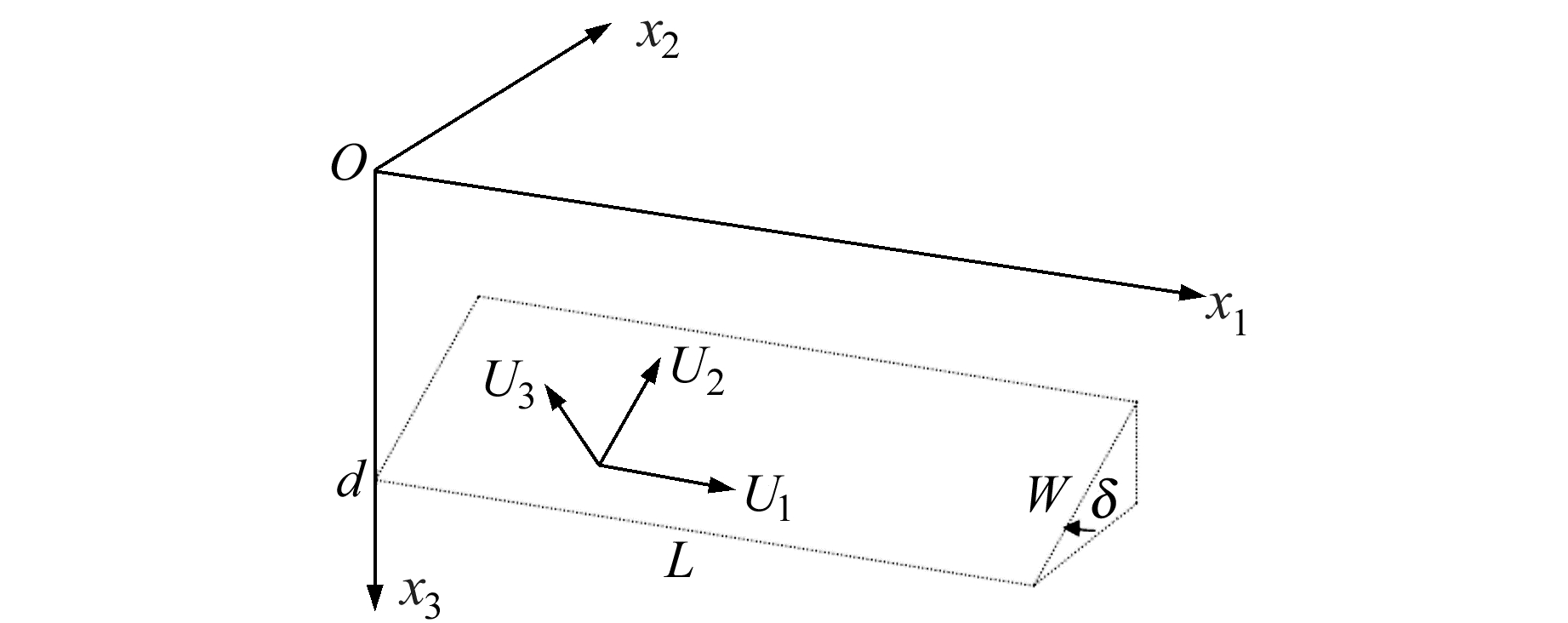
定义直角坐标系(x1, x2, x3)如图 3所示,x1轴位于地表,与“等效位错”的走向平行,x3轴取向下为正。将孕震区存有的闭锁剪力等效为一个(0, 0, d)处的位错源,取“等效位错”对应的面元Σ,其中位错三分量U1、U2、U3分别代表等效位错源的走滑、倾滑与张性分量。
|
图 3 “等效位错”模型示意图 Fig. 3 Finite rectangle equivalent dislocation |
根据Okubo[9]理论,等效位错(U1, U2, U3)引起的重力变化Δg可表示为:
| $ \begin{array}{l} \Delta g({x_1}, {x_2}) = \\ f({x_1}, {x_2};{U_1}, {U_2}, {U_3}, L, W, {\rm{dep}}, \delta, \varphi, X, Y) = \\ \rho G{\rm{ }}{U_1}{S_g}\left( {\xi, \eta } \right) + {U_2}{D_g}\left( {\xi, \eta } \right) + {U_3}{T_g}\left( {\xi, \eta } \right)\parallel \end{array} $ | (3) |
式中各符号含义参见文献[9]。值得注意的是,由于震源闭锁,地表不存在相关垂直运动和张裂效应。f(x1, x2; U1, U2, U3, L, W, dep, δ, φ, X, Y)表示Δg本质上是一个关于等效位错的位错三分量(U1、U2、U3)、长度(L)、宽度(W)、中心的位置(X、Y)、顶部与地表的距离(dep)及走向(φ)与倾角(δ)的函数。
式(1)~(3)构成闭锁剪力定量化模型的基本框架:利用式(3)反演解算出等效位错,再利用式(2)解算出孕震矩(对应闭锁剪力)。
3 姚安地震的闭锁剪力模型参数确定孕震模型参数应只根据震前能获得的信息(即震前重力变化)来选取,预测参数可与震后资料作对比,进行验证。由此可知,等价于闭锁剪力的“位错”引起的地表重力变化是基于一系列参数的函数——f(x1, x2; U1, U2, U3, L, W, dep, δ, φ, X, Y)。考虑到反演问题的多解性,本文仅对“等效位错”的力学模型参数U1、U2、U3进行反演,反演前需对其他几何模型参数进行选取。
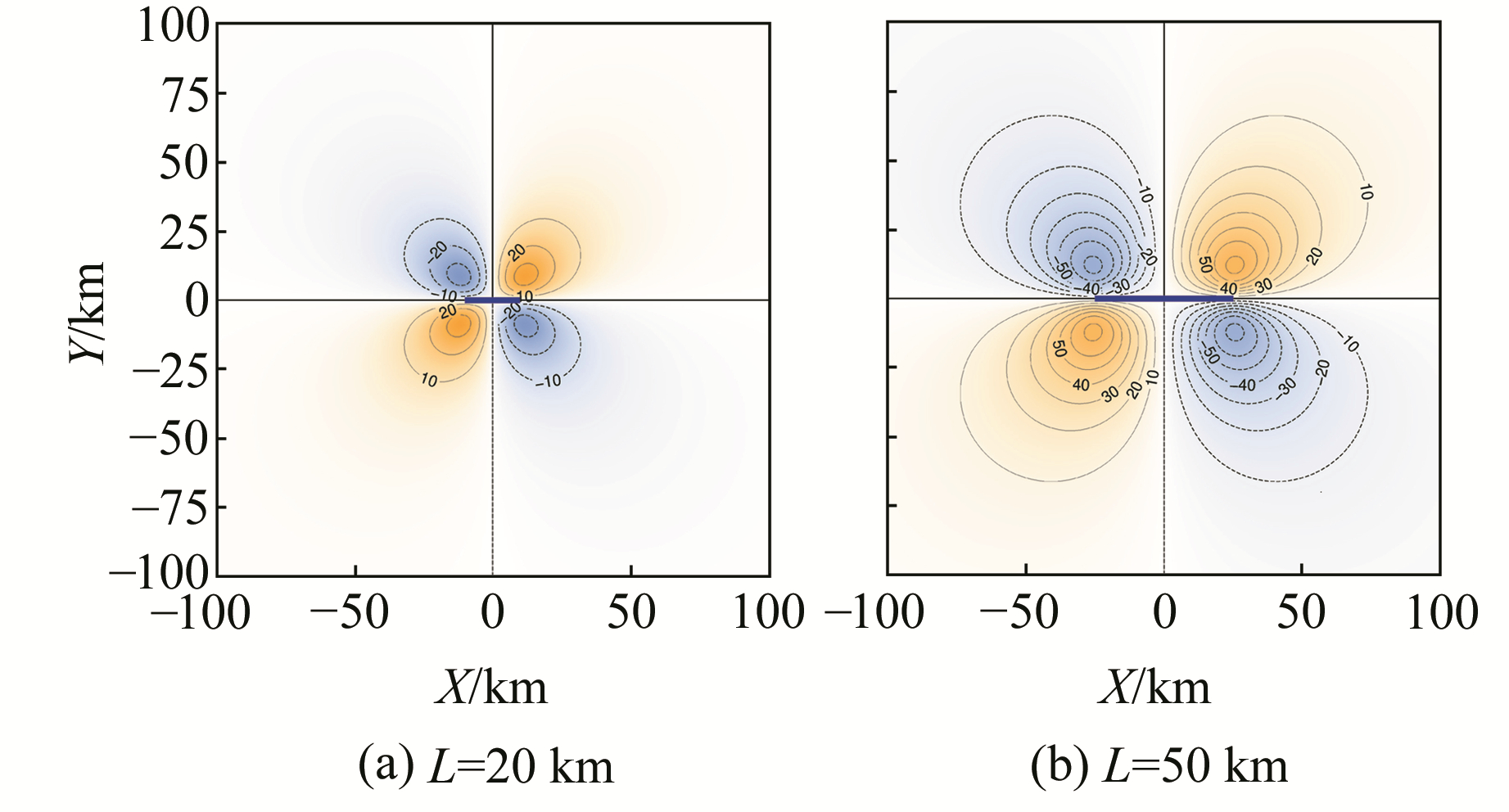
3.1 孕震几何模型参数的确定 3.1.1 长度(L)及走向(φ)的选取不失一般性,取等效位错的倾角为90°,顶部距地表的距离为10 km,走向为90°,位错三分量分别为U1 = -10 m, U2 = 0 m, U3 = 0 m,介质密度为2.67 g/cm3。随着等效位错长度的变化,等效位错对地表重力的影响如图 4所示,图中蓝色实线为等效位错在地表的投影。
|
图 4 走滑型等效位错(δ = 90°, dep = 10 km, U1 = -10 m, U2 = U3 = 0)产生的重力变化 Fig. 4 The gravity changes caused by strike-slip equivalent fault(δ = 90°, dep = 10 km, U1 = -10 m, U2 = U3 = 0) |
从图 4可以看出,等效位错一侧的一对正负重力变化极值之间连线方位角即为等效位错的走向,其长度与等效位错的长度相等。对于姚安MS6.0地震的震前重力图像,其对应的等效位错走向为西侧正极值点与南侧负极值点之间的连线与正北方向的夹角(313.6°),其对应的等效位错长度为西侧正极值点与南侧负极值点之间的距离(58.1 km)。等效位错的宽度,根据经验,大震断层的长宽比一般为2 :1[10],因此取29.05 km。
3.1.2 中心位置(X, Y)及倾角(δ)的选取不失一般性,取等效位错的长度为50 km,顶部距地表的距离为10 km,走向为90°,位错三分量为U1 = -10 m, U2 = 0 m, U3 = 0 m,介质密度为2.67 g/cm3。随着倾角的变化,等效位错对地表重力的影响如图 5所示,图中4个极值点的中心为2条红线的交点。

|
图 5 走滑型等效位错(L = 50 km, W = 25 km, dep = 10 km, U1 = -10 m, U2 = U3 = 0)产生的重力变化 Fig. 5 The gravity changes caused by strike-slip equivalent fault(L = 50 km, W = 25 km, dep = 10 km, U1 = -10 m, U2 = U3 = 0) |
从图 5可以看出,随着等效位错倾角的改变,位错两侧的重力变化极值之间的比值也随之变化,但4个极值点的对称中心仍然与等效位错中心的位置接近。通过数值模拟程序,可确定等效位错的倾角与等效位错两侧重力变化极值之比的关系,结果见表 1。
|
|
表 1 δ与等效位错两侧重力变化的2个正极值之间比值的关系 Tab. 1 The relationship between δ and the ratio of the positive gravity change peak on the both side of dislocation |
对于姚安MS6.0地震的震前重力图像,等效位错中心位于重力变化四象限图形的对称中心,即西侧正极值点与东侧正极值点之间连线的中点(25.51°N,100.94°E)。重力图像中西侧正极值点与东侧正极值点的重力值之比为0.769 2,对应的倾角为84.8°。
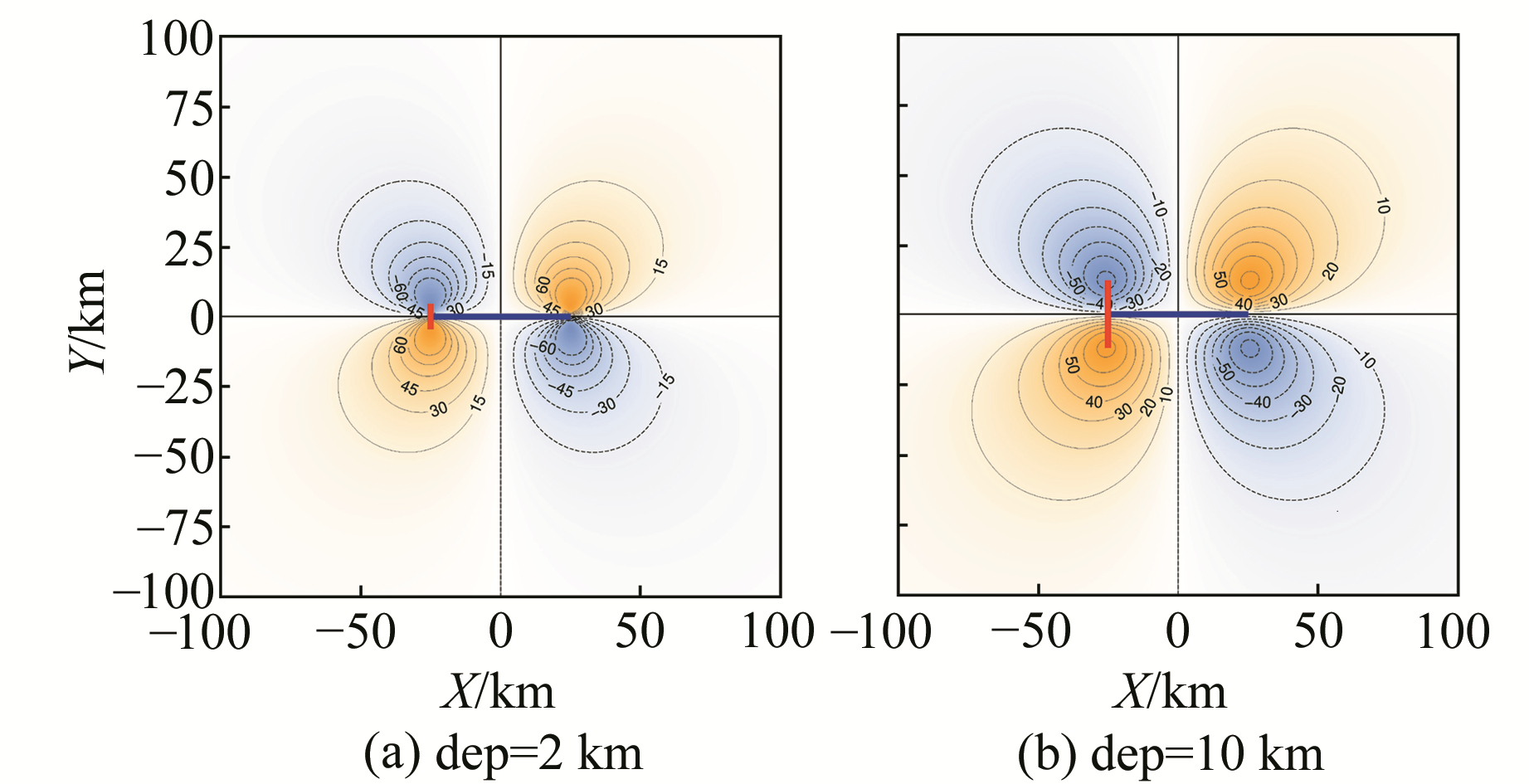
3.1.3 顶部与地表距离(dep)的选取不失一般性,取等效位错的长度为50 km,倾角为90°,走向为90°,位错三分量为U1 = -10 m, U2 = 0 m, U3 = 0 m,介质密度为2.67 g/cm3。随着等效位错顶部与地表距离的变化,等效位错对地表重力的影响如图 6所示,图中蓝色实线为等效位错在地表的投影,红色实线为等效位错两侧一对正负极值点之间的连线。
|
图 6 走滑型等效位错(L = 50 km, δ = 90°, U1 = -10 m, U2 = U3 = 0)产生的重力变化 Fig. 6 The gravity changes caused by strike-slip fault source(L = 50 km, δ = 90°, U1 = -10 m, U2 = U3 = 0) |
从图 6可以看出,在等效位错的长度和倾角已经确定的情况下,随着等效位错顶部与地表距离的改变,等效位错两侧一对正负重力极值点之间的距离与等效位错长度之比也随之改变。通过数值模拟程序,可确定等效位错顶部与地表的距离和该比值之间的关系(表 2)。
|
|
表 2 Dep与长度比之间的关系 Tab. 2 The relationship between dep and the ratio of distances |
对于姚安MS6.0地震的震前重力图像,震中西侧正极值点和南侧负极值点之间的距离与等效位错长度的比值为1.989 6,其对应的等效位错顶部与地表的距离为13.5 km。
综上所述,将根据震前重力变化选取的模型参数与其他学者对姚安MS6.0地震震源机制解的研究结果[11-13]进行对比,结果见表 3。
|
|
表 3 模型参数与姚安MS6.0地震震源机制解 Tab. 3 Model parameters and focal mechanism solution of Yao'an MS6.0 earthquake |
由表 3可知,在发震位置上,各震源机制解的结果与选取的模型参数都较为接近;在倾角上,各震源机制解分布在77°~88°之间,模型参数为84.8°也落在这一区间内;在走向上,模型参数与震源机制解的结果差距为20°。这可能是由于在孕震过程中,重力前兆反映的是整个区域能量积累的程度,而主震的震源机制解与地震发生处具体的地质构造有关,因此与模型参数有一定差别。
3.2 姚安地震“孕震体强度”反演将前文确定的几何模型参数输入闭锁剪力模型进行反演迭代计算,反演采用稳健-贝叶斯最小二乘算法,可以减弱原始数据中粗差的影响[14],得到的位错三分量U1、U2、U3如表 4所示。
|
|
表 4 模型参数的反演结果 Tab. 4 The inversion results of model parameters |
由反演出的位错三分量计算其对应的孕震能量为(μ取3×1010 Pa):
| $ {M_0} = \mu UA = 8.11 \times {10^{17}}{\rm{N \cdot m}} $ |
其对应的矩震级为[15]:
| $ {M_w} = \frac{2}{3}{\rm{lg}}{M_0}-6.06 = 5.88 $ |
这一结果比美国USGS给出的姚安地震矩震级MW5.7稍大,说明孕震体中所积累的能量并没有在主震中完全释放,这可能也是震后余震多发的主要原因。
4 结语1) 姚安MS6.0地震的“闭锁剪力”效应产生的重力场变化与“走滑位错”密度变化效应产生的重力场变化在空间分布、正负方向上具有一致性,故其孕震类型为走滑型。
2) 为了能在震前指导地震分析预报工作,闭锁剪力模型的几何参数应通过重力变化前兆图像来选取。对于像姚安MS6.0地震这类孕震类型为走滑型的地震,可将重力变化四象限的中心选取为孕震源的中心,即为预测地震的震中位置。
3) 采用稳健-贝叶斯最小二乘算法来进行闭锁剪力模型力学参数的反演,其结果能较好地量化重力前兆中包含的孕震信息。闭锁剪力模型计算的孕震矩震级与实际发震的矩震级相接近,表明该方法能够为预测地震震级提供参考。
4) 本文在利用定量化模型对走滑型孕震模式的地震进行预测方面作出了初步探索,对非走滑型孕震类型的地震进行预测时是否仍能获得较好的结果,尚需进一步深入研究。
| [1] |
申重阳, 李辉, 孙少安, 等. 重力场动态变化与汶川MS8.0地震孕育过程[J]. 地球物理学报, 2009, 52(10): 2547-2557 (Shen Chongyang, Li Hui, Sun Shao'an, et al. Dynamic Variations of Gravity and the Preparation Process of the Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2009, 52(10): 2547-2557 DOI:10.3969/j.issn.0001-5733.2009.10.013)
(  0) 0) |
| [2] |
祝意青, 闻学泽, 孙和平, 等. 2013年四川芦山MS7.0地震前的重力变化[J]. 地球物理学报, 2013, 56(6): 1887-1894 (Zhu Yiqing, Wen Xueze, Sun Heping, et al. Gravity Changes before the Lushan, Sichuan, MS = 7.0 Earthquake of 2013[J]. Chinese Journal of Geophysics, 2013, 56(6): 1887-1894)
(  0) 0) |
| [3] |
祝意青, 李铁明, 郝明, 等. 2016年青海门源MS6.4地震前重力变化[J]. 地球物理学报, 2016, 59(10): 3744-3752 (Zhu Yiqing, Li Tieming, Hao Ming, et al. Gravity Changes before the Menyuan, Qinghai MS6.4 Earthquake of 2016[J]. Chinese Journal of Geophysics, 2016, 59(10): 3744-3752 DOI:10.6038/cjg20161019)
(  0) 0) |
| [4] |
申重阳, 吴云, 甘家思. 从地壳运动角度分析大陆强震机理的一种物理方法[J]. 中国地震, 2001, 17(1): 70-81 (Shen Chongyang, Wu Yun, Gan Jiasi. A Physical Method of Analyzing the Continental Strong Earthquake Mechanism from Crustal Movement[J]. Earthquake Research in China, 2001, 17(1): 70-81 DOI:10.3969/j.issn.1001-4683.2001.01.008)
(  0) 0) |
| [5] |
申重阳, 谈洪波, 郝洪涛, 等. 2009年姚安MS6.0地震重力场前兆变化机理[J]. 大地测量与地球动力学, 2011, 31(2): 17-22 (Shen Chongyang, Tan Hongbo, Hao Hongtao, et al. Mechanism of Precursory Gravity Change before Yao'an MS6.0 Earthquake in 2009[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 17-22)
(  0) 0) |
| [6] |
祝意青, 郭树松, 刘芳. 攀枝花6.0级地震前后区域重力场变化[J]. 大地测量与地球动力学, 2010, 30(4): 8-11 (Zhu Yiqing, Guo Shusong, Liu Fang. Variation of Gravity Field before and after Panzhihua MS6.1 and Yao'an MS6.0 Earthquakes[J]. Journal of Geodesy and Geodynamics, 2010, 30(4): 8-11)
(  0) 0) |
| [7] |
Aki K, Richards P G. 定量地震学[M]. 北京: 地震出版社, 1986 (Aki K, Richards P G. Quantitive Seismology[M]. Beijing: Seismological Press, 1986)
(  0) 0) |
| [8] |
Maruyama T. On the Force Equivalent of Dynamic Elastic Elastic Dislocation with Reference to the Earthquake Mechanism[J]. Bulletin of the Earthquake Research Institute, 1963, 41: 467-488
(  0) 0) |
| [9] |
Okubo S. Gravity and Potential Changes Due to Shear and Tensile Faults in a Half-Space[J]. Journal of Geophysical Research, 1992, 97(B5): 7137 DOI:10.1029/92JB00178
(  0) 0) |
| [10] |
燕乃玲, 李辉, 申重阳. 丽江地震前后重力场变化的有限矩形位错模型分析[J]. 地震学报, 2003, 25(2): 172-181 (Yan Nailing, Li Hui, Shen Chongyang. Analyses on Gravity Variation before and after the Lijiang Earthquake Based on a Finite Rectangular Dislocation Model[J]. Acta Seismologica Sinica, 2003, 25(2): 172-181 DOI:10.3321/j.issn:0253-3782.2003.02.007)
(  0) 0) |
| [11] |
秦双龙, 张建国, 廖丽霞. 2009年云南姚安6.0级地震震源机制与发震构造的分析研究[J]. 内陆地震, 2009, 26(1): 52-61 (Qin Shuanglong, Zhang Jianguo, Liao Lixia. Analysis on Focal Mechanism and Seismogenic Structures of Yao'an Earthquake with MS6.0, 2009[J]. Inland Earthquake, 2009, 26(1): 52-61)
(  0) 0) |
| [12] |
潘睿, 盛书中, 万永革. 2009年姚安地震断层面参数的确定[J]. 华北地震科学, 2015, 33(2): 63-68 (Pan Rui, Sheng Shuzhong, Wan Yongge. Seismic Fault Plane Parameters Estimating of 2009 Yao'an Earthquake[J]. North China Earthquake Sciences, 2015, 33(2): 63-68 DOI:10.3969/j.issn.1003-1375.2015.02.011)
(  0) 0) |
| [13] |
李君, 王勤彩. 2009年姚安MS6.0地震序列发震断层及应力场特征[J]. 地震学报, 2016, 38(2): 199-207 (Li Jun, Wang Qincai. Seismogenic Faults and Stress Field Characteristics of MS6.0 Yao'an Earthquake Sequence in 2009[J]. Acta Seismology Sinica, 2016, 38(2): 199-207)
(  0) 0) |
| [14] |
申重阳, 李辉, 付广裕. 丽江7.0级地震重力前兆模式研究[J]. 地震学报, 2003, 25(2): 163-171 (Shen Chongyang, Li Hui, Fu Guangyu. Study on a Gravity Precursor Mode of Lijiang Earthquake with MS = 7.0[J]. Acta Seismology Sinica, 2003, 25(2): 163-171 DOI:10.3321/j.issn:0253-3782.2003.02.006)
(  0) 0) |
| [15] |
戴志阳, 刘斌, 查显杰, 等. 震级标度的不一致与震源的复杂性[J]. 地球物理学进展, 2008, 23(3): 705-709 (Dai Zhiyang, Liu Bin, Zha Xianjie, et al. Erathquake Scaling Disagreement and Complexity of Seismic Source[J]. Progress in Geophysics, 2008, 23(3): 705-709)
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2019, Vol. 39
2019, Vol. 39


