2. 中国地质大学(武汉)地质过程与矿产资源国家重点实验室,武汉市鲁磨路388号,430074
重力勘探与时变重力测量的每次重要革新都依赖于重力传感器或测量仪器及测量系统、测量平台的成功研发[1-2],例如从物理摆到金属或石英弹簧重力仪、从钮秤到重力梯度仪、从地面与船载测量到航空与卫星测量等。下一代重力传感器或测量仪器及测量系统、测量平台可能是小型化、轻便化的基于微电子机械系统的重力仪[3],也可能是重力位三阶梯度张量测量系统[4]。
Balakin等[4]于1997年在俄罗斯的Dulkyn项目中最早提出测量地球重力位场的三阶导数及其时变场理论。在此基础上,Brieden等[5]于2010年提出OPTIMA地球时变重力场卫星测量计划。Fantino等[6]和Fukushima[7]于2009~2013年阐述重力位一阶至三阶梯度的球谐表达式及其计算问题。Rosi等[8]于2015年在实验室内利用冷原子干涉技术成功实现重力位三阶垂直梯度测量,在大地测量领域的地球重力场建模方向掀起一股针对重力位三阶梯度张量的理论研究[9]、仿真模拟[10]及正演计算[11]热潮。此外,由于对局部质量源具有高度敏感性,重力位三阶垂直梯度也被实验室用于测量万有引力常数[12]。并且,地球重力位三阶垂直梯度不等于0,致使重力垂直梯度随高度存在非线性变化特征[13]。
在重力勘探领域,DiFrancesco等[14]于2009年提出重力位三阶梯度张量的航空测量概念。事实上,因为有助于压制区域场、突出局部场、增强弱信号及区分水平叠加异常,重力位二阶导数自1951年就被用于重力异常数据的处理与解释推断[15]。基于重力异常转换处理所得的传统二阶导数并不会增加数据本身包含的场信息量,而实际的重力位三阶梯度张量测量将直接提升场及场源的信息量。本文从地球物理学的重力勘探角度出发,详细介绍重力位三阶梯度张量异常及其对场源的识别能力,为我国开展相关研究提供参考。
1 重力位三阶梯度张量基本原理如图 1(a)所示,以观测面上一点O为坐标原点,X轴与Y轴在水平观测面内分别指向地理北和地理东,Z轴与X、Y轴满足右手坐标系。对于地下任意形状的地质体,如球体(图 1(b))与直立长方体(图 1(c)),假设其剩余密度为Δρ,体积为Ω,令Q(ξ, η, ζ)为地质体内部任一点,该点处的体积元为dΩ = dξdηdζ,质量元为dm = ΔρdΩ,则地质体在观测点P(x, y, z)处的引力位异常ΔV为:
| $ \Delta V\left( x, y, z \right) = G\iiint\limits_{\mathit{\Omega }}{\frac{\Delta \rho }{l}\text{d}\mathit{\Omega }}~ $ | (1) |

|
图 1 场源与观测点几何示意图 Fig. 1 Geometrical sketch map of the source and the observation point |
式中,G为万有引力常数,l为观测点与质量元之间的距离,即
| $ l = \sqrt{{{\left( x-\xi \right)}^{2}}+{{\left( y-\eta \right)}^{2}}+{{\left( z-\zeta \right)}^{2}}} $ | (2) |
根据位场理论[16]可得,重力异常矢量Δg(Δgx, Δgy, Δgz)在3个坐标轴方向的分量为:
| $ \left\{ \begin{align} &~\Delta {{g}_{x}} = \frac{\partial \Delta V}{\partial x} = -G\iiint\limits_{\mathit{\Omega }}{\frac{\Delta \rho \left( x-\xi \right)}{{{l}^{3}}}}~ \\ &\Delta {{g}_{y}} = \frac{\partial \Delta V}{\partial y} = -G\iiint\limits_{\mathit{\Omega }}{\frac{\Delta \rho \left( y-\eta \right)}{{{l}^{3}}}} \\ &\Delta {{g}_{z}} = \frac{\partial \Delta V}{\partial z} = -G\iiint\limits_{\mathit{\Omega }}{\frac{\Delta \rho \left( z-\zeta \right)}{{{l}^{3}}}}~ \\ \end{align} \right. $ | (3) |
重力位二阶梯度张量异常ΔT的各个元素为重力异常矢量Δg(Δgx, Δgy, Δgz)在3个坐标轴方向的一阶导数,即
| $ \Delta {{T}_{\alpha \beta }} = \frac{\partial {{g}_{\alpha }}}{\partial \beta }, \text{ }\forall \left\{ \alpha, \beta \right\}\in \left\{ x, y, z \right\} $ | (4) |
由于
| $ \begin{align} &\Delta {{T}_{\alpha \beta }} = \frac{\partial }{\partial \alpha }\frac{\partial \Delta V}{\partial \beta } = \frac{\partial }{\partial \beta }\frac{\partial \Delta V}{\partial \alpha } = \Delta {{T}_{\beta \alpha }}, \\ &\ \ \ \ \ \ \ \ \ \ \forall \left\{ \alpha, \beta \right\}\in \left\{ x, y, z \right\} \\ \end{align} $ | (5) |
张量矩阵ΔT为对称矩阵,即满足ΔTxy = ΔTyx、ΔTxz = ΔTzx与ΔTyz = ΔTzy。又由于重力异常位在场源外部空间满足拉普拉斯方程,即
| $ {{\nabla }^{2}}(\Delta V) = \Delta {{T}_{xx}}+\Delta {{T}_{yy}}+\Delta {{T}_{zz}} = 0 $ | (6) |
因此,张量矩阵ΔT仅有5个独立元素。
重力位三阶梯度张量异常ΔW的各个元素为ΔTαβ在3个坐标轴方向的一阶导数,即
| $ \Delta {{W}_{\alpha \beta \gamma }} = \frac{\partial \Delta {{T}_{\alpha \beta }}}{\partial \gamma }~, \ \forall \left\{ \alpha, \beta, \gamma \right\}\in \left\{ x, y, z \right\} $ | (7) |
由式(7)可知,ΔW共有33 = 27个元素。与式(5)同理,由于
| $ \begin{align} &\Delta {{W}_{\alpha \beta \gamma }} = \frac{\partial }{\partial \alpha }\frac{\partial }{\partial \beta }\frac{\partial \Delta V}{\partial \gamma } = \frac{\partial }{\partial \alpha }\frac{\partial }{\partial \gamma }\frac{\partial \Delta V}{\partial \beta } = \\ &\ \ \ \ ~\Delta {{W}_{\alpha \gamma \beta }} = \frac{\partial }{\partial \beta }\frac{\partial }{\partial \alpha }\frac{\partial \Delta V}{\partial \gamma } = \Delta {{W}_{\beta \alpha \gamma }} = \\ &\frac{\partial }{\partial \beta }\frac{\partial }{\partial \gamma }\frac{\partial \Delta V}{\partial \alpha } = \Delta {{W}_{\beta \gamma \alpha }} = \frac{\partial }{\partial \gamma }\frac{\partial }{\partial \alpha }\frac{\partial \Delta V}{\partial \beta } = \Delta {{W}_{\gamma \alpha \beta }} = \\ &\frac{\partial }{\partial \gamma }\frac{\partial }{\partial \beta }\frac{\partial \Delta V}{\partial \alpha } = \Delta {{W}_{\gamma \beta \alpha }}, \forall \left\{ \alpha, \beta, \gamma \right\}\in \left\{ x, y, z \right\} \\ \end{align} $ | (8) |
张量矩阵ΔW也满足对称性。又根据式(6)可得:
| $ \begin{align} &\frac{\partial }{\partial \gamma }{{\nabla }^{2}}(\Delta V) = ~\frac{\partial }{\partial \gamma }(\Delta {{T}_{xx}}+\Delta {{T}_{yy}}+\Delta {{T}_{zz}}) = 0, \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \gamma \in \left\{ x, y, z \right\}~ \\ \end{align} $ | (9) |
因此,张量矩阵ΔW仅有7个独立元素。
根据以上分析可知,重力位的零阶梯度张量即为重力位标量本身;一阶梯度张量即为重力矢量;二阶梯度张量为3行3列的实对称矩阵,表示重力分量在各个方向上的变化率;三阶梯度张量为三阶三维实对称张量,表示重力梯度在各个方向上的变化率(图 2)。
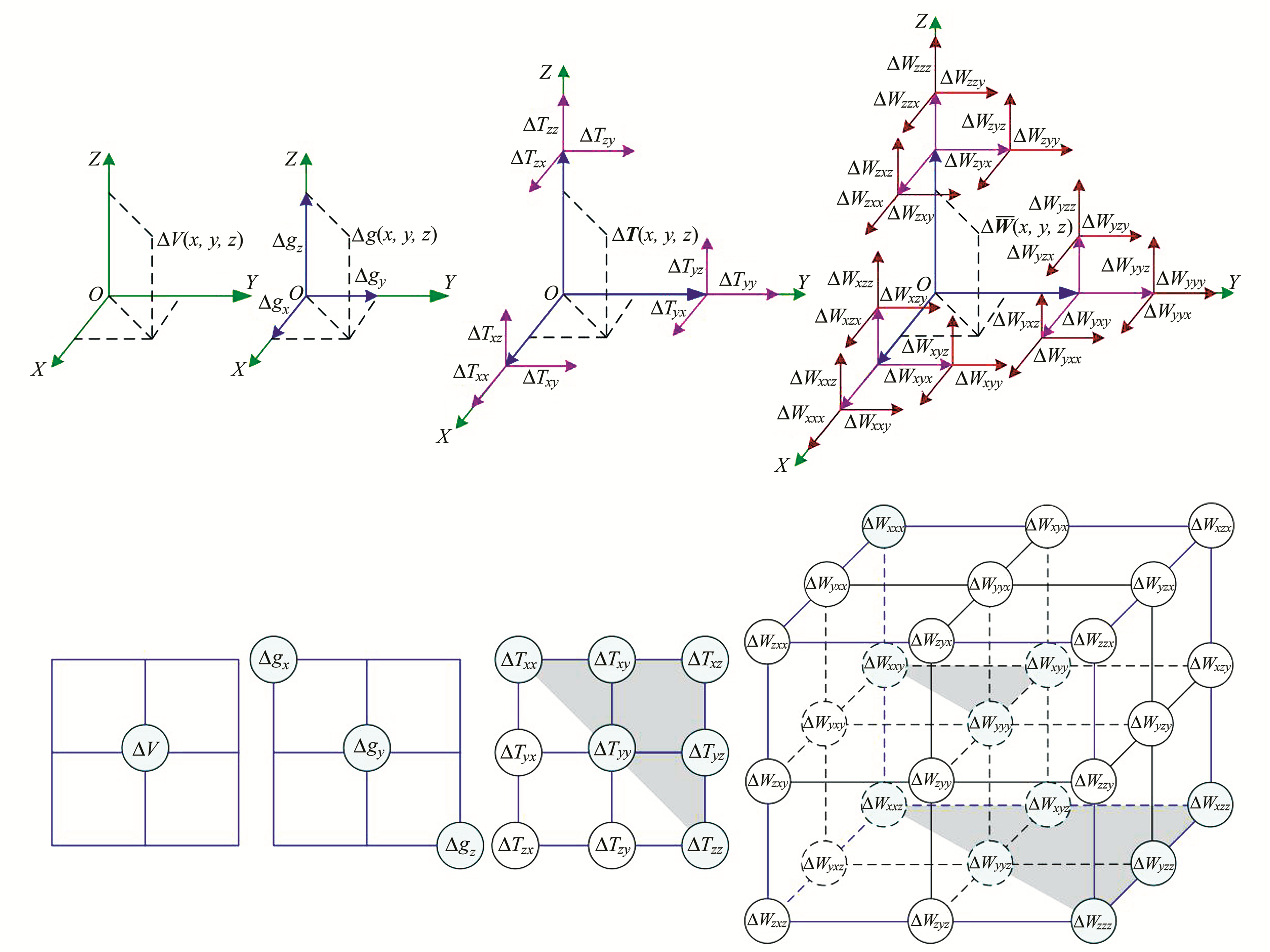
|
图 2 重力位零阶至三阶梯度张量的物理含义(上)和元素对称关系(下) Fig. 2 Sketch map of physical meanings(upper panel) and symmetry relations(lower panel) among elements for zero-, first-, second- and third-order gradient tensors of the gravitational potential |
在实际的数据处理与解释推断中,往往采用点源作为虚拟场源,将一些近于等轴状的地质体近似为密度均匀的球体。如图 1(b)所示,令球心坐标为Q(x0, y0, z0),半径为R,剩余密度为Δρ,则其剩余质量M为4πR3Δρ/3,观测点坐标为P(x, y, z),l为观测点与球心之间的距离,即l = [(x0-x)2+(y0-y)2+(z0-z)2]1/2。将物理参数与几何参数代入式(1)、式(3)、式(4)及式(7),经过推导与简化可得均匀球体的重力位零阶至三阶梯度张量异常解析表达式,结果见表 1。
|
|
表 1 均匀球体的重力位零阶至三阶梯度张量异常解析表达式 Tab. 1 Analytical expressions of zero-, first-, second- and third-order gradient tensors of the anomalous gravitational potential of the homogenous spheroid |
令密度均匀的球心埋深为D = 100 m,球心平面投影为(0 m, 0 m),半径为R = 50 m,剩余密度为Δρ = 500 kg/m3,代入表 1的解析表达式中,计算得到z = 0 m观测面上的重力位零阶至三阶梯度张量异常空间分布,结果见图 3。可以看出,由零阶至三阶梯度张量,异常场的水平衰减越来越快,说明对地下场源的水平分辨能力越来越高;随着张量的独立元素个数的增多,异常场空间分布形态类型越来越多样化,这意味着在相同的测点分布情况下,高阶梯度张量能够捕获更多的场源信息。

|
图 3 均匀球体的重力位零阶至三阶梯度张量异常空间分布 Fig. 3 Spatial distributions of zero-, first-, second- and third-order gradient tensors of the anomalous gravitational potential of the homogenous spheroid |
重力方法的实际勘探能力受测点三维空间分布(包括均匀性、稀疏性与观测高度等)、测量误差及非目标影响的改正精度、测区范围、测量物理场类型的综合影响。为简化分析,假定观测面为平面、观测范围无限大、测点均匀分布且足够密集,不考虑非目标的影响,仅分析测量误差与物理场类型对场源埋深、剩余质量、水平位置与几何形态的探测能力。场源埋深与观测高度均是相对地面而言,两者之间的距离在物理本质上影响观测场,故本文将观测面置于地面,即z = 0 m,仅讨论场源埋深因素。
3.1 探测深度与剩余质量的能力分析为便于分析,仅选择ΔV、Δgz、ΔTzz、ΔWzzz等4个具有单极大值的物理量,并且假设球心平面投影与观测面分别为(0 m, 0 m)与z = 0 m,则ΔV、Δgz、ΔTzz、ΔWzzz的最大值与半幅值宽度如表 2所示。可以看出,从零阶至三阶梯度,其幅值随埋深z0按照z0-1、z0-2、z0-3与z0-4的规律衰减,而剩余质量与幅值呈线性关系。若测量区域较大、测量点分布均匀且密集,则探测能力仅由观测误差决定,但受埋深与剩余质量的共同影响[17-19]。
|
|
表 2 ΔV、Δgz、ΔTzz与ΔWzzz的最大值与半幅值宽 Tab. 2 Maximum and width of half amplitude of ΔV, Δgz, ΔTzz and ΔWzzz |
若重力异常极大值大于3倍的观测误差,则该异常的可靠性至少大于99.73%[20]。以此为依据,按照表 2所示公式计算,若Δgz的误差为1×10-8 m/s2,则可探测1 m、100 m与10 km深度处约4.5×102 kg、4.5×106 kg与4.5×1010 kg的最小剩余质量;若ΔTzz的误差为1×10-9 s-2,则可探测1 m、100 m与10 km深度处约7.5 kg、7.5×106 kg与7.5×1012 kg的最小剩余质量;若ΔWzzz的误差为1×10-11 m-1s-2,则可探测1 m、100 m与10 km深度处约2.5×10-2 kg、2.5× 106 kg与4.5×1014 kg的最小剩余质量。由此可见,重力位三阶梯度张量对于浅部的剩余质量非常敏感,探测能力较强;反之,越往深部,由于快速衰减,探测能力相对较差。
3.2 探测场源水平位置的能力分析观测场对场源水平位置的敏感性决定了水平分辨率,即区分水平叠加异常的能力。由表 2可知,从ΔV、Δgz、ΔTzz到ΔWzzz,其半幅值宽度逐渐减小,一方面意味着重力位三阶梯度具有更高的水平分辨能力,区分距离较近的相邻异常体引起叠加异常的能力越来越强,区分能力随埋深均呈线性变化;另一方面说明对于相同的探测目标,重力位三阶梯度的测点点距应该为二阶梯度的3/4、重力的1/2。
3.3 探测场源几何形态的能力分析若观测面为平面,则场源几何形状直接影响观测场的空间分布形态,这与场源构造指数[21]有关,也与场源埋深有关。为了说明重力位三阶梯度张量区分场源几何形态的能力,此处采用直立棱柱体模型[22],如图 1(c)所示。
首先,令直立棱柱体的长(a)、宽(b)与高(c)分别为500 m、300 m与300 m,顶面埋深h为100 m,剩余密度为Δρ = 500 kg/m3,计算得到在z = 0 m平面上的场分布(图 4)。然后,采用球体模型,令其中心埋深及剩余质量与直立棱柱体相同,使得两者之间的差异仅体现在场源几何形态上,计算得到均匀球体在z = 0 m平面上的场分布,其形态与图 3所示一致。从零阶至三阶梯度,对场源几何形态的区分能力逐渐增强,本质上是水平分辨能力逐渐增强。

|
黑色矩形框表示直立棱柱体在观测面上的水平投影 图 4 均匀直立棱柱体(顶面埋深h为100 m)重力位零阶至三阶梯度张量异常空间分布 Fig. 4 Spatial distributions of zero-, first-, second- and third-order gradient tensors of the anomalous gravitational potential of the right rectangular prism with homogenous density and top surface depth h of 100 m |
依然采用上述模型,仅改变顶面埋深,使h为3 000 m,计算得到均匀直立棱柱体在z = 0 m平面上的场分布(图 5)。对比图 3与图 5可以看出,此时2个模型所致场在空间分布形态上的差异比较微弱,若埋深继续增大,则该直立棱柱体与球体模型在观测场方面几乎可以完全等价。这说明场的空间分布形态还与场源埋深有关,场源越深,观测场对场源形态的识别能力越弱,本质上对场源水平分辨的能力也越弱。

|
黑色矩形框表示直立棱柱体在观测面上的水平投影 图 5 均匀直立棱柱体(顶面埋深h为3 000 m)重力位零阶至三阶梯度张量异常空间分布 Fig. 5 Spatial distributions of zero-, first-, second- and third-order gradient tensors of the anomalous gravitational potential of the right rectangular prism with homogenous density and top surface depth h of 3 000 m |
1) 重力位三阶梯度张量异常共有27个元素,由于张量对称性,独立元素降为10个;又由于在场源以外空间重力位异常满足拉普拉斯方程,独立元素仅有7个。每个元素表示重力某分量在某方向空间变化的加速度,即重力梯度的空间变化率。
2) 推导得到球体与点源的重力位零阶至三阶梯度张量解析表达式及重力位零阶至三阶垂直梯度的幅值与半幅值宽随深度的变化关系。理论分析与模型实验表明,在重力位零阶至三阶梯度张量中,三阶梯度张量随场源与观测点之间的距离增大,衰减最快,因此具有如下特征:对场源埋深变化具有最高的敏感性;对浅部的剩余质量探测能力最强,对深部的剩余质量探测能力最弱;对场源的水平分辨能力与区分场源几何形态的能力均随场源埋深增大而减小,但重力曲率张量的分辨能力最强;重力曲率张量的独立元素个数最多,场空间分布形态的类型也最多样,说明在相同的测点分布情况下,三阶梯度张量能够捕获更多的场与场源信息,尤其是重力场的短波成分与浅部的剩余质量。
3) 重力位三阶梯度张量由于对场源具有高度敏感性,其应用领域将非常广泛,例如资源勘探、地质填图、环境(诸如地下空洞、岩溶与地面塌陷)与工程地球物理(尤其是城市与浅地表地球物理)及考古、地下质量迁移监测(诸如火山与地震及断裂活动性监测、滑坡监测、地下水与煤炭自燃及石油开采监测、海洋介质多尺度时空运动监测等)、重力场建模、无源导航与定位、潜艇避障与探潜、隐藏军事设施与掩埋未爆炸物等探测、万有引力常数测定等,但距离实际应用尚需开展更多工作,如理论研究(如张量特征值与不变量分析等)、仪器与系统研发、数据预处理(如滤波、非探测目标影响改正等)、数据转换处理、场源解释等。
| [1] |
Nabighian M N, Ander M E, Grauch V J S, et al. Historical Development of the Gravity Method in Exploration[J]. Geophysics, 2005, 70(6): 63-89 DOI:10.1190/1.2133785
(  0) 0) |
| [2] |
Camp M, Viron O, Watlet A, et al. Geophysics from Terrestrial Time-Variable Gravity Measurements[J]. Reviews of Geophysics, 2017, 55(4): 938-992 DOI:10.1002/rog.v55.4
(  0) 0) |
| [3] |
Moddlemiss R P, Samarelli A, Paul D J, et al. Measurement of the Earth Tides with a MEMS Gravimeter[J]. Nature, 2016, 531(7 596): 614-617
(  0) 0) |
| [4] |
Balakin A B, Daishev R A, Murzakhanov Z G, et al. Laser-Interferometric Detector of the First, Second and Third Derivatives of the Potential of the Earth Gravitational Field[J]. Izvestiya Vysshikh Uchebnykh Zavedenii, Seriya Geologiyai Razvedka, 1997(1): 101-107
(  0) 0) |
| [5] |
Brieden P, Muller J, Flury J, et al.The Mission OPTIMA—Novelties and Benefit[R]. Geotechnologien, Potsdam, 2010
(  0) 0) |
| [6] |
Fantino E, Casotto S. Methods of Harmonic Synthesis for Global Geopotential Models and Their First-, Second- and Third-Order Gradients[J]. Journal of Geodesy, 2009, 83(7): 595-619 DOI:10.1007/s00190-008-0275-0
(  0) 0) |
| [7] |
Fukushima T. Recursive Computation of Oblate Spheroidal Harmonics of Second Kind and Their First-, Second-, and Third-Order Derivatives[J]. Journal of Geodesy, 2013, 87(4): 303-309 DOI:10.1007/s00190-012-0599-7
(  0) 0) |
| [8] |
Rosi G, Cacciapuoti L, Sorrentino F, et al. Measurements of the Gravity-Field Curvature by Atom Interferometry[J]. Physical Review Letters, 2015, 114(1)
(  0) 0) |
| [9] |
Ghobadi-Far K, Sharifi M A, Sneeuw N. 2D Fourier Series Representation of Gravitational Functionals in Spherical Coordinates[J]. Journal of Geodesy, 2016, 90(9): 871-881 DOI:10.1007/s00190-016-0916-7
(  0) 0) |
| [10] |
Sharifi M A, Romeshkani M, Tenzer R. On Inversion of the Second- and Third-Order Gravitational Tensors by Stokes' Integral Formula for a Regional Gravity Recovery[J]. Studia Geophysica et Geodaetica, 2017, 61(3): 453-468 DOI:10.1007/s11200-016-0831-7
(  0) 0) |
| [11] |
Deng X L, Shen W B. Evaluation of Optimal Formulas for Gravitational Tensors up to Gravitational Curvatures of a Tesseroid[J]. Surveys in Geophysics, 2018, 39(3): 365-399 DOI:10.1007/s10712-018-9460-8
(  0) 0) |
| [12] |
Rothleitner C, Francis O. Measuring the Newtonian Constant of Gravitation with a Differential Free-Fall Gradiometer: A Feasibility Study[J]. Review of Scientific Instruments, 2014, 85(4): 469-526
(  0) 0) |
| [13] |
陈钊, 李辉, 邢乐林, 等. 重力垂直梯度非线性变化研究[J]. 大地测量与地球动力学, 2014, 34(2): 27-30 (Chen Zhao, Li Hui, Xing Lelin, et al. Study on Non-Linear Variation of Vertical Gradient of Gravity[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 27-30)
(  0) 0) |
| [14] |
DiFrancesco D, Meyer T J, Christensen A, et al.Gravity Gradiometry—Today and Tomorrow[C]. 11th SAGA Biennial Technical Meeting and Exhibition, Swaziland, 2009
(  0) 0) |
| [15] |
Elkins T A. The Second Derivative Method of Gravity Interpretation[J]. Geophysics, 1951, 16(1): 29-50
(  0) 0) |
| [16] |
曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005 (Zeng Hualin. Gravity Field and Gravity Exploration[M]. Beijing: Geological Publishing House, 2005)
(  0) 0) |
| [17] |
Li X. Vertical Resolution: Gravity Versus Vertical Gravity Gradient[J]. The Leading Edge, 2001, 20(8): 901-904 DOI:10.1190/1.1487304
(  0) 0) |
| [18] |
王庆宾, 江东, 赵东明, 等. 重力垂直梯度测量探测能力的正演[J]. 测绘科学技术学报, 2011, 28(3): 262-264 (Wang Qingbin, Jiang Dong, Zhao Dongming, et al. Underground Vacancy Detection Based on Vertical Gravity Gradient Measurements[J]. Journal of Geomatics Science and Technology, 2011, 28(3): 262-264)
(  0) 0) |
| [19] |
王谦身, 张赤军, 蒋福珍. 微重力测量:理论、方法与应用[M]. 北京: 科学出版社, 1995 (Wang Qianshen, Zhang Chijun, Jiang Fuzhen. Microgravimetry: Theory, Method and Applications[M]. Beijing: Science Press, 1995)
(  0) 0) |
| [20] |
Liu Y X. Evaluation and Extraction of Weak Gravity and Magnetic Anomalies[J]. Applied Geophysics, 2007, 4(4): 288-293 DOI:10.1007/s11770-007-0041-8
(  0) 0) |
| [21] |
Stavrev P, Reid A. Degrees of Homogeneity of Potential Fields and Structural Indices of Euler Deconvolution[J]. Geophysics, 2007, 72(1): L1-L12
(  0) 0) |
| [22] |
邱峰, 杜劲松, 陈超. 矩形棱柱体重力位三阶梯度张量正演计算公式[J]. 大地测量与地球动力学, 2019, 39(3): 313-316 (Qiu Feng, Du Jinsong, Chen Chao. Forward Modeling Formulae for Third-Order Gradient Tensor of Gravitational Potential Caused by the Right Rectangular Prism[J]. Journal of Geodesy and Geodynamics, 2019, 39(3): 313-316)
(  0) 0) |
2. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
 2019, Vol. 39
2019, Vol. 39

