2. 东莞中子科学中心,广东省东莞市中子源路1号,523803
随着我国航空航天、造船、核能、轨道交通、大科学装置等领域对工件制造及装配的精度要求越来越高,相应地对仪器的测量精度提出了非常高的要求[1-4]。影响激光跟踪仪自身测量精度的因素为测角误差和测距误差[5],现有的提升激光跟踪仪测量精度的方法主要有2种:一种是对测角和测距系统误差进行补偿。由于测角和测距误差主要是由跟踪仪内部部件几何位置不正确造成的,激光跟踪仪厂家都建立有相应的仪器几何误差模型,并在仪器系统软件中开发了专门的仪器误差补偿模块,通过在测量现场对激光跟踪仪进行双面测量、测距零点测量等来进行误差补偿。有学者研究通过正多面棱体和自准直仪相结合的方法对激光跟踪仪的测角误差进行标定[6],以及通过激光干涉仪对激光跟踪仪的测距进行标定[7]。另外一种是改进测量方法,如采用激光跟踪仪测边法。根据激光跟踪仪测角精度低、测距精度高的特点,只采用跟踪仪测量的距离值作为观测值,充分发挥激光跟踪仪测距精度高的优势,彻底消除测角误差大的影响,以提升激光跟踪仪的点位测量精度[8]。但是,这种方法缺少角度测量值信息,所需测站数成倍增加,同时不同的网形对最终的测量精度影响很大。
在现代仪器制造中,部件的制造和装配精度已经不像以前那么重要,重要的是设法提高仪器的精密性和重复性[9]。激光跟踪仪的测量重复性一般是测量误差的1/2,因此,针对激光跟踪仪测量重复性高的特点,提出基于长度标准装置对激光跟踪仪的观测值进行标定,然后将标定值用于激光跟踪仪实际测量的误差修正,努力使激光跟踪仪的测量精度超越现有水平。
1 基于长度标准装置对激光跟踪仪进行标定的方法长度标准装置主要由精密导轨系统、长度测量系统、环境监测系统和自动控制系统4个部分组成。精密导轨系统为直线导轨;长度测量系统利用激光干涉仪作为测量基准;环境监测系统用于采集温度参数,供系统实时补偿[10]。长度标准装置工作方法:干涉仪的反射球放置在工作台上,工作台由电机驱动沿直线导轨运行,移动的距离由激光干涉系统测量。在中国计量院有80 m长的长度标准装置、在中航工业北京长城计量测试技术研究所有30 m长的长度标准装置以及在中国散裂中子源国家大科学装置建设有20 m长的长度标准装置。参考我国国家质量监督检验检疫总局发布的“JJF1242-2010激光跟踪三维坐标测量系统校准规范”以及美国机械工程师协会发布的“ASME B89.4.19-2006 Performance Evaluation of Laser-Based Spherical Coordinate Measurements Systems”标准规范,这些长度标准装置通常被用来作为激光跟踪仪校准以及现场性能检查的一种手段[11-12]。本文提出基于长度标准装置对激光跟踪仪进行标定的方法,在对仪器校准提供示值误差的基础上,利用激光跟踪仪测量重复性高的特点,对激光跟踪仪的实际测量误差进行修正,提升激光跟踪仪的测量精度。
基于长度标准装置对激光跟踪仪进行标定的方法如下:将激光干涉仪固定在长度标准装置上,将激光跟踪仪稳固架设,使长度标准装置的运动平台在导轨上运动,在运动路径上选取若干停留点作为标定点。激光干涉仪对标定点的激光干涉仪反射球进行测量获得长度观测值,激光跟踪仪对标定点的激光跟踪仪反射球进行测量,获得水平方向观测值、天顶距观测值、边长观测值。变换激光跟踪仪的架设方位,重复上述测量步骤,使激光跟踪仪的水平方向观测值覆盖0°~360°范围、天顶距观测值覆盖激光跟踪仪俯仰测量范围、边长观测值覆盖激光跟踪仪测量半径(图 1)。
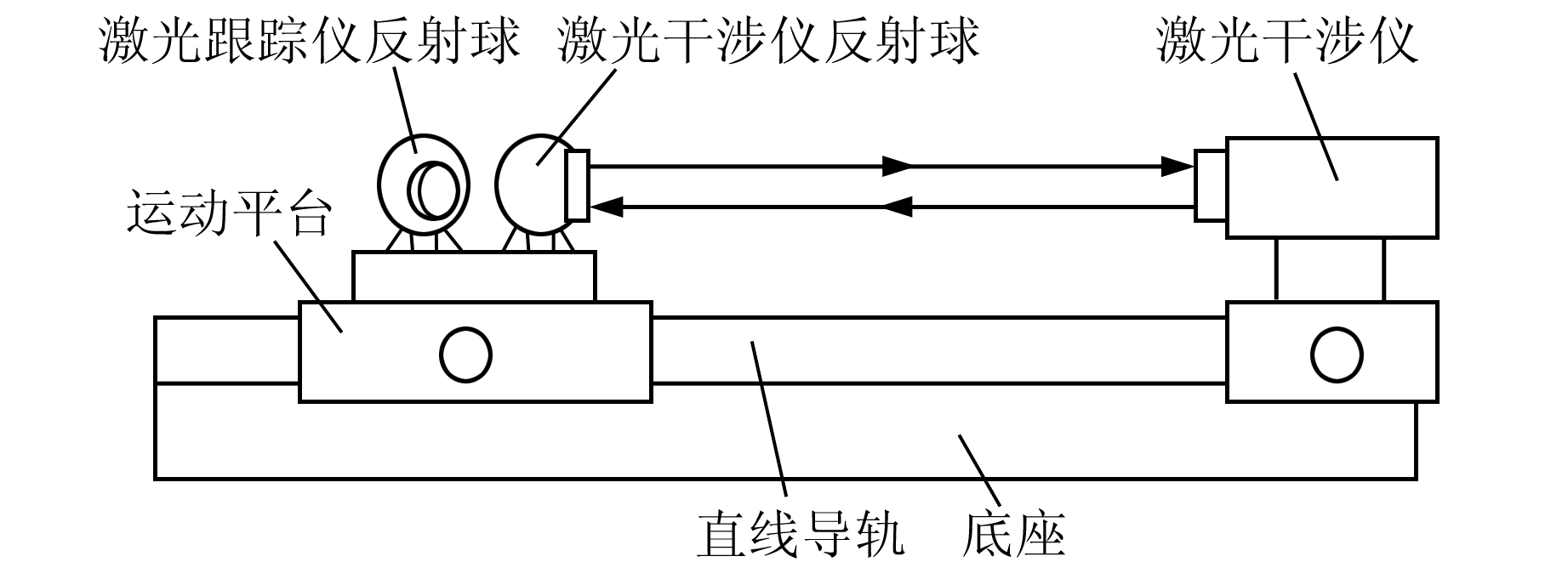
|
图 1 基于长度标准装置对激光跟踪仪标定 Fig. 1 Calibration for the laser tracker based on the length standard device |
根据激光跟踪仪对观测值标定的要求以及长度标定装置的摆放,具体的标定方法分为如下4种:1)水平测量标定。长度标准装置水平放置,激光跟踪仪距离长度标准装置至少2 m远,并稳固架设在长度标准装置中部位置。2)垂直测量标定。长度标准装置垂直放置,激光跟踪仪距离长度标准装置至少2 m远,并稳固架设在长度标准装置中部位置。3)纵向测量标定。长度标准装置水平放置,激光跟踪仪稳固架设在长度标准装置的端头。4)对角线测量标定。长度标准装置与地面成45°夹角倾斜放置,激光跟踪仪距离长度标准装置至少2 m远,并稳固架设在长度标准装置中部位置。激光跟踪仪和激光干涉仪分别对标定点进行测量获得对标定点的观测值。
通过上述对标定点的测量,可以得到激光跟踪仪的水平方向观测值、天顶距观测值、边长观测值以及相对应的激光干涉仪的长度观测值, 建立激光跟踪仪和激光干涉仪标定观测的数学模型,计算得到标定点观测值的改正数以及标定点观测值平差值的精度。
2 基于长度标准装置对激光跟踪仪进行标定的数学模型首先建立激光跟踪仪仪器坐标系、装置测站坐标系、激光干涉仪坐标系,在这3个坐标系下对激光跟踪仪及激光干涉仪的各个观测值进行数学模型建立及分析。
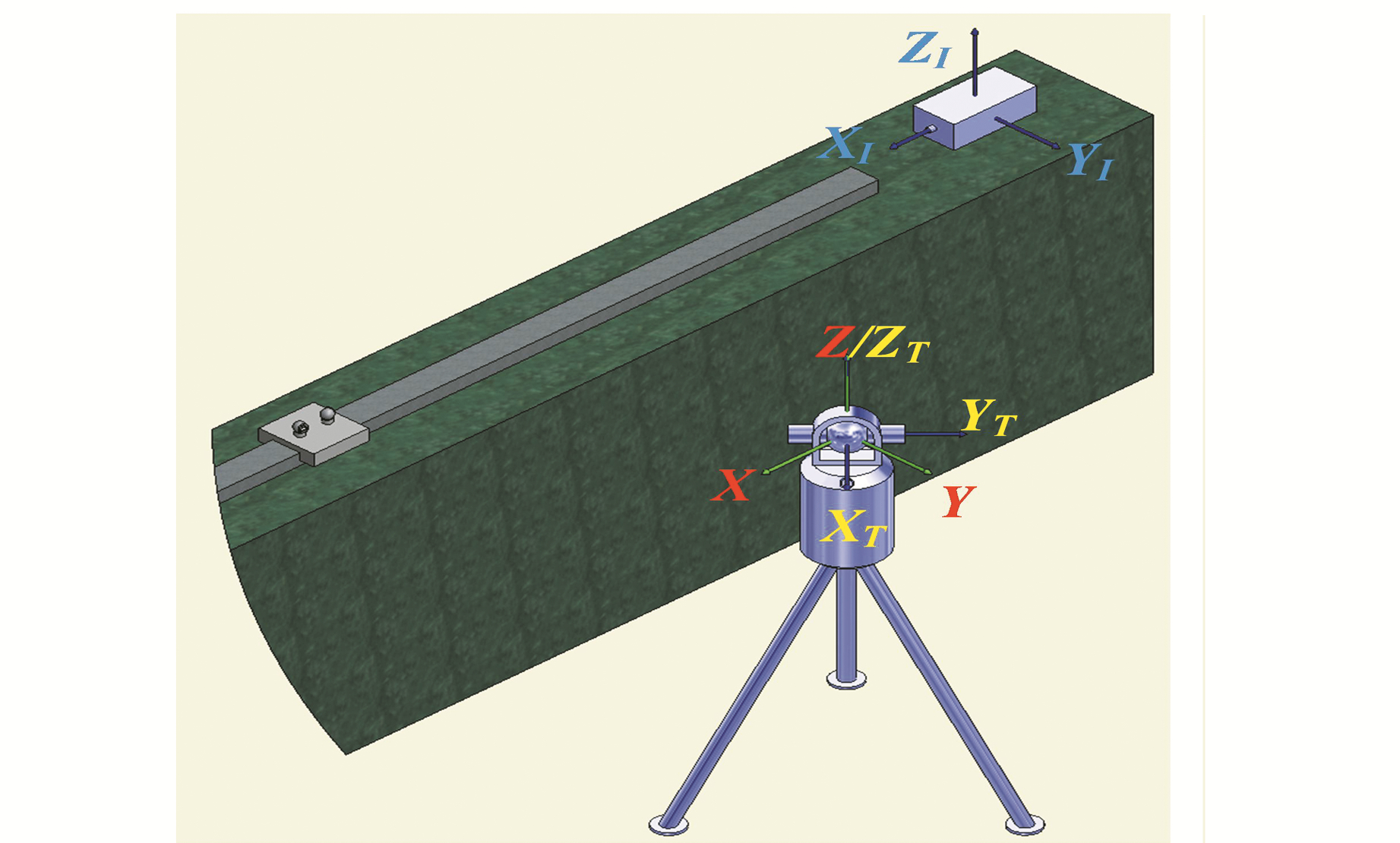
|
图 2 坐标系之间的关系 Fig. 2 The relation between the coordinate systems |
激光跟踪仪仪器坐标系:以激光跟踪仪仪器中心点为原点,以竖轴为第一轴Z轴,以激光跟踪仪的零方向为第二轴X轴(激光跟踪仪的零方向是指水平方向观测值为零的方向,一般特定指向跟踪仪的基点)。在仪器坐标系下目标的三维坐标为(XT, YT, ZT):
| $ \left\{ {\begin{array}{*{20}{l}} {{X_T} = S\sin \beta \cos \alpha }\\ {{Y_T} = S\sin \beta \sin \alpha }\\ {{Z_T} = S\cos \beta } \end{array}} \right. $ | (1) |
式中,α为水平方向观测值,β为天顶距观测值,S为斜距。
装置测站坐标系:以激光跟踪仪仪器中心点为原点,以竖轴为第一轴Z轴,以激光干涉仪的激光束方向为第二轴X轴。以装置测站坐标系为全局坐标系,在装置测站坐标系下目标的三维坐标为(X, Y, Z):
| $ \left\{ {\begin{array}{*{20}{l}} {X = S\sin \beta \cos (\alpha + W)}\\ {Y = S\sin \beta \sin (\alpha + W)}\\ {Z = S\cos \beta } \end{array}} \right. $ | (2) |
式中,W为激光跟踪仪的零方向在装置测站坐标系下的方位角。
激光干涉仪坐标系:以激光干涉仪的测距零点为原点,以激光干涉仪的激光束方向为第一轴X轴,以装置测站坐标系的Y轴为第二轴Y轴。激光干涉仪坐标系与装置测站坐标系的转化关系为:
| $ \left[ {\begin{array}{*{20}{c}} {{X_I}}\\ {{Y_I}}\\ {{Z_I}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_\Delta }}\\ {{Y_\Delta }}\\ {{Z_\Delta }} \end{array}} \right] + {\mathit{\boldsymbol{R}}_y}\left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] $ | (3) |
其中,
式中,R为激光干涉仪坐标系与装置测站坐标系转化的旋转角,在激光干涉仪坐标系下目标的三维坐标为(XI, YI, ZI)。
2.1 激光跟踪仪水平方向函数模型与误差方程对于标定点在激光跟踪仪下的水平方向观测值,有观测方程
| $ \begin{array}{l} {\alpha _i} + {v_{\alpha i}} = \arctan \frac{{Y_i^0}}{{X_i^0}} - \frac{{Y_i^0}}{{{{(D_i^0)}^2}}}{{\hat x}_i} + \\ \;\;\;\;\;\;\;\;\;\frac{{X_i^0}}{{{{(D_i^0)}^2}}}{{\hat y}_i} - ({W^0} + \hat w) \end{array} $ |
其中,
| $ {v_{\alpha i}} = - \frac{{\rho ''Y_i^0}}{{{{(D_i^0)}^2}}}{\hat x_i}{\rm{ + }}\frac{{\rho ''X_i^0}}{{{{(D_i^0)}^2}}}{\hat y_i} - \hat w - {l_{\alpha i}} $ | (4) |
对于标定点在激光跟踪仪下的天顶距观测值,有观测方程
| $ {\beta _i} + {v_{\beta i}} = \arccos \frac{{Z_i^0}}{{S_i^0}} + \frac{{X_i^0Z_i^0}}{{{{(S_i^0)}^2}D_i^0}}{\hat x_i} + \frac{{Y_i^0Z_i^0}}{{{{(S_i^0)}^2}D_i^0}}{\hat y_i} - \frac{{D_i^0}}{{{{(S_i^0)}^2}}}{\hat z_i} $ |
其中,
| $ {v_{\beta i}} = \frac{{\rho ''X_i^0Z_i^0}}{{{{(S_i^0)}^2}D_i^0}}{\hat x_i} + \frac{{\rho ''Y_i^0Z_i^0}}{{{{(S_i^0)}^2}D_i^0}}{\hat y_i} - \frac{{\rho ''D_i^0}}{{{{(S_i^0)}^2}}}{\hat z_i} - {l_{\beta i}} $ | (5) |
对于标定点在激光跟踪仪下的边长观测值,有观测方程为
| $ {v_{Si}} = \frac{{X_i^0}}{{S_i^0}}{\hat x_i} + \frac{{Y_i^0}}{{S_i^0}}{\hat y_i} + \frac{{Z_i^0}}{{S_i^0}}{\hat z_i} - {l_{Si}} $ | (6) |
对于标定点在激光干涉仪下的长度观测值,有观测方程为:
| $ \begin{array}{l} {v_{Li}} = \cos {R^0}{{\hat x}_i} - \sin {R^0}{{\hat z}_i} - \\ (X_i^0\sin {R^0} + Z_i^0\cos {R^0})\hat r + {{\hat x}_\Delta } - {l_{Li}} \end{array} $ | (7) |
假设激光跟踪仪测量有n个标定点,则根据式(4)~(7),可得到误差方程的矩阵形式[13]:
| $ \mathop {\mathit{\boldsymbol{V}}}\limits_{4n \times 1} = \mathop {\mathit{\boldsymbol{B}}}\limits_{4n \times (3n + 3)} \mathop {\hat {\mathit{\boldsymbol{x}}}}\limits_{(3n + 3) \times 1} - \mathop {\mathit{\boldsymbol{l}}}\limits_{4n \times 1} $ | (8) |

|
| $ \mathop {\mathit{\boldsymbol{V}}}\limits_{4n \times 1} = \\\;{\left[ {\begin{array}{*{20}{c}} {{v_{\alpha 1}}}&{{v_{\beta 1}}}&{{v_{S1}}}&{{v_{L1}}}& \cdots &{{v_{\alpha i}}}&{{v_{\beta i}}}&{{v_{Si}}}&{{v_{Li}}}& \cdots &{{v_{\alpha n}}}&{{v_{\beta n}}}&{{v_{Sn}}}&{{v_{Ln}}} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathop {\hat {\mathit{\boldsymbol{x}}}}\limits_{(3n + 3) \times 1} = \\\;{\left[ {\begin{array}{*{20}{c}} {{{\hat x}_1}}&{{{\hat y}_1}}&{{{\hat z}_1}}& \cdots &{{{\hat x}_i}}&{{{\hat y}_i}}&{{{\hat z}_i}}& \cdots &{{{\hat x}_n}}&{{{\hat y}_n}}&{{{\hat z}_n}}&{\hat w}&{\hat r}&{{{\hat x}_\Delta }} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathop {\mathit{\boldsymbol{l}}}\limits_{4n \times 1} = \\\;{\left[ {\begin{array}{*{20}{c}} {{l_{\alpha 1}}}&{{l_{\beta 1}}}&{{l_{S1}}}&{{l_{L1}}}& \cdots &{{l_{\alpha i}}}&{{l_{\beta i}}}&{{l_{Si}}}&{{l_{Li}}}& \cdots &{{l_{\alpha n}}}&{{l_{\beta n}}}&{{l_{Sn}}}&{{l_{Ln}}} \end{array}} \right]^{\rm{T}}} $ |
由于带有误差的观测值是一种随机变量, 因此,在对误差方程进行平差求解时需要考虑其随机模型。随机模型是描述平差问题中的随机量及其相互间统计相关性质的模型。在上述平差函数模型中,观测值αi、βi、Si、Li为随机量,模型中的参数
在平差前,一般根据仪器的标称精度来定权。以Leica AT960激光跟踪仪[14]为例,其角度精度为15 μm+6 μm/m,因此,其水平方向精度为
由于激光跟踪仪测量有n个标定点,那么,总共有4n个观测方程,有3n+3个未知参数,观测方程的个数应不小于未知参数个数,即n≥3。根据最小二乘原理,式(8)中的
| $ \mathit{\boldsymbol{\hat x}} = {({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} $ | (9) |
将式(9)代入式(8),可以得到每个观测值的改正数:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B}}{({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} - \mathit{\boldsymbol{l}} $ | (10) |
单位权方差σ02的估值
| $ {\mathit{\boldsymbol{D}}_{\hat \alpha \hat \beta \hat S}}_{\hat L \times \hat \alpha \hat \beta \hat S\hat L} = \hat \sigma _0^2\mathit{\boldsymbol{B}}{({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}} $ | (11) |
由式(10)和式(11)可以得到激光跟踪仪标定点Pi的观测值αi、βi、Si,及其对应的改正数vαi、vβi、vSi和观测值的平差值的精度σαi、σβi、σSi。针对激光跟踪仪测量重复性高的特点, 当激光跟踪仪标定完进行现场测量时,提出采用对标定点观测值进行插值的方法对测量点M的观测值αm、βm、Sm进行误差修正, 从而对激光跟踪仪进行误差补偿。由于激光跟踪仪的测距精度高,其精度主要是受测角精度的限制,因此,应重点对激光跟踪仪的角度误差进行修正。插值改正的方法为:以激光跟踪仪仪器坐标系的原点为球心,构建一个球体,将标定点和目标点都映射在这个球体表面上(图 3)。

|
图 3 激光跟踪仪误差改正 Fig. 3 Error correction for laser tracker |
以对目标点M的水平方向观测值进行插值为例,选取其周围4个相邻且其水平方向观测值的平差值的精度比先验精度高的标定点Pi、Pj、Pk、Pl进行插值计算,得到目标点M水平方向观测值αm的改正数:vαm=vαiQαi+vαjQαj+vαkQαk+vαlQαl,其中Qα为标定点水平方向改正数对应的权,与标定点观测值的平差值的方差及目标点与标定点的距离等有关。测量点M经过改正后的水平方向观测值为
为了验证本文方法的可行性,采用长度标准装置对Leica AT401激光跟踪仪进行水平方向标定及标定后的精度测试(见表 1)。水平方向标定时,激光跟踪仪距离长度标准装置5 m远,共观测21个标定点,每个标定点相距约1 m,覆盖水平方向的观测范围为91°~333°,通过计算得到标定点水平方向的改正数。为了测试激光跟踪仪标定后的测量精度,在长度标准装置上布设有21个目标点M1~M21,激光跟踪仪相对于长度标准装置的方位保持不变,目标点与标定点的位置也基本一致。将M1点置为起始点,采用激光干涉仪可以测量得到M2~M21点到M1点之间的距离;同时,通过激光跟踪仪对目标点进行观测得到各目标点的坐标,利用目标点的坐标反算也可以得到M2~M21点到M1点之间的距离,将坐标反算得到的距离分别与干涉仪测量的距离进行对比,得到差值1。由于激光跟踪仪测量得到目标点之间的距离主要受其水平方向误差的影响,因此,本例只对目标点的水平方向进行改正,得到目标点改正后的水平方向及水平方向改正后的坐标。同样,将改正后的坐标反算得到的距离分别与干涉仪测量的距离进行对比,得到差值2。对表 1中的差值1和差值2进行统计,差值1的RMS为19.5 μm,差值2的RMS为10.2 μm。由此得出,激光跟踪仪经过误差补偿后,其测量精度得到一定提高。
|
|
表 1 激光跟踪仪误差补偿后精度测试 Tab. 1 Accuracy testing after the error correction for laser tracker |
本文利用激光跟踪仪测量重复性高的特点, 从理论上详细给出了对激光跟踪仪观测值进行误差修正的方法,同时,通过一组简单的实验测试,初步验证这种方法对激光跟踪仪测量精度的提高是可行有效的,后续将开展更详细的测试完善。在本方法中,通过引入方位角W进行激光跟踪仪仪器坐标系与装置测站坐标系的转换,引入旋转角R进行装置测站坐标系与激光干涉仪坐标系的转化,建立激光跟踪仪对标定点的观测值与激光干涉仪对标定点的观测值之间的数学关系,从而彻底消除了激光跟踪仪反射镜的运动轴线与激光干涉仪的激光束方向不平行造成的余弦误差的影响,降低了对长度标准装置的导轨直线度和激光干涉仪的光束调整精度的要求,从而降低了长度标准装置的建造标准,使得长度标准装置走向平民化,在普通单位即可开展仪器校准和误差补偿。同时,在对仪器校准提供示值误差的基础上,通过观测值的后验方差阵直接计算出仪器的水平方向、天顶距、边长的测量误差,这对仪器的性能评估具有重要意义。
| [1] |
李广云, 范百兴. 精密工程测量技术及其发展[J]. 测绘学报, 2017, 46(10): 1 742-1 751 (Li Guangyun, Fan Baixing. The Development of Precise Engineering Surveying Technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 742-1 751)
(  0) 0) |
| [2] |
梁静, 董岚, 罗涛, 等. BEPCⅡ储存环激光跟踪仪测量精度统计及先验误差的确定[J]. 测绘科学, 2013, 38(6): 182-184 (Liang Jing, Dong Lan, Luo Tao, et al. Precision Statistics of Laser Tracker in BEPCⅡ Storage Ring and Calculation of Mean Square Error of Unit Weight[J]. Science of Surveying and Mapping, 2013, 38(6): 182-184)
(  0) 0) |
| [3] |
马娜, 董岚, 梁静, 等. 中国散裂中子源直线加速器控制网测量及精度研究[J]. 测绘通报, 2016(1): 104-107 (Ma Na, Dong Lan, Liang Jing, et al. Measurement and Research of Control Network's Accuracy of CSNS Linear Accelerator[J]. Bulletin of Surveying and Mapping, 2016(1): 104-107)
(  0) 0) |
| [4] |
梁静, 董岚, 王铜, 等. 激光跟踪仪在CSNS高频腔预准直中的应用[J]. 地理空间信息, 2017, 15(3): 12-13 (Liang Jing, Dong Lan, Wang Tong, et al. Application of Laser Tracker in the Pre-Alignment of RF Cavity for CSNS[J]. Geospatial Information, 2017, 15(3): 12-13)
(  0) 0) |
| [5] |
孙海丽, 姚连璧, 周跃寅, 等. 激光跟踪仪测量精度分析[J]. 大地测量与地球动力学, 2015, 35(1): 177-181 (Sun Haili, Yao Lianbi, Zhou Yueyin, et al. Analysis of Measurement Accuracy of Laser Tracker[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 177-181)
(  0) 0) |
| [6] |
卢荣胜, 李万红, 劳达宝, 等. 激光跟踪仪测角误差补偿[J]. 光学精密工程, 2014, 22(9): 2 299-2 305 (Lu Rongsheng, Li Wanhong, Lao Dabao, et al. Angular Error Compensation for Laser Tracker[J]. Optics and Precision Engineering, 2014, 22(9): 2 299-2 305)
(  0) 0) |
| [7] |
丁蕾, 周维虎, 王亚伟. 样条函数在激光跟踪仪测距补偿中的应用[J]. 光电工程, 2012, 39(3): 78-82 (Ding Lei, Zhou Weihu, Wang Yawei. Spline Function for Distance Error Compensation of Laser Tracker[J]. Opto-Electronic Engineering, 2012, 39(3): 78-82 DOI:10.3969/j.issn.1003-501X.2012.03.014)
(  0) 0) |
| [8] |
范百兴, 李广云, 李佩臻, 等. 利用激光干涉测距三维网的加权秩亏自由网平差[J]. 武汉大学学报:信息科学版, 2015, 40(2): 222-226 (Fan Baixing, Li Guangyun, Li Peizhen, et al. Adjustment of a Laser Interferometer 3D Rank-Defect Free-Network[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 222-226)
(  0) 0) |
| [9] |
周维虎.大尺寸空间坐标测量系统精度理论若干问题的研究[D].合肥: 合肥工业大学, 2000 (Zhou Weihu. Research on the Precision Theory of Large-Scale Coordinate Measuring Systems[D]. Hefei: Hefei University of Technology, 2000)
(  0) 0) |
| [10] |
马骊群.大尺寸计量校准技术研究及在量值传递中的应用[D].大连: 大连理工大学, 2007 (Ma Liqun. Research on Large-Scale Dimensional Calibration and Its Application in Measurement Transfer Chain[D]. Dalian: Dalian University of Technology, 2007)
(  0) 0) |
| [11] |
JJF 1242-2010, 激光跟踪三维坐标测量系统校准规范[S].2010 (JJF 1242-2010, Calibration Specification for Laser Tracker 3-Dimensional Measuring System[S].2010)
(  0) 0) |
| [12] |
The American Society of Mechanical Engineers. ASME B89.4.19-2006, Performance Evaluation of Laser-Based Spherical Coordinate Measurements Systems[S].2006
(  0) 0) |
| [13] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2003 (Surveying Adjustment Discipline Group, School of Geodesy and Geomatics, Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2003)
(  0) 0) |
| [14] |
Metrology H. Leica Absolute Tracker AT960 Brochure[EB/OL]. http://www.hexagonmi.com/products/laser-tracker-systems/leica-absolute-tracker-at960/.2017
(  0) 0) |
| [15] |
Automated Precision Inc. XD Laser Brochure[EB/OL]. https://www.apisensor.com/products/mth/xd-laser/.2017
(  0) 0) |
2. Dongguan Neutron Science Center, 1 Zhongziyuan Road, Dongguan 523803, China
 2019, Vol. 39
2019, Vol. 39

