2019, Vol. 39
矩形棱柱体重力位三阶梯度张量正演计算公式
1. 中国地质大学(武汉)地球物理与空间信息学院地球内部多尺度成像湖北省重点实验室，武汉市鲁磨路388号，430074;
2. 中国地质大学(武汉)地质过程与矿产资源国家重点实验室，武汉市鲁磨路388号，430074
2. 中国地质大学(武汉)地质过程与矿产资源国家重点实验室，武汉市鲁磨路388号，430074
摘要：基于位场理论推导出矩形棱柱体重力位三阶梯度张量正演计算的解析公式，采用理论模型对比解析公式与重力位二阶梯度张量中心差分的计算结果，并以是否满足拉普拉斯方程作为检验标准，对推导公式的正确性进行验证。
关键词：三阶梯度张量；重力位；矩形棱柱体；正演计算；解析表达式
作为最常用的模型构建基本单元，矩形棱柱体被广泛用于重力资料的正演模拟、数据处理、反演与解释中[1]。从重力位至重力矢量再到重力梯度，矩形棱柱体的正演计算解析公式已经基本得以确定[2-6]，而对于重力二次导数或重力位三阶梯度张量、矩形棱柱体的正演计算解析公式还未见报道。鉴于重力位三阶梯度张量在未来的广泛应用前景，本文首先经过推导得到矩形棱柱体重力位三阶梯度张量的正演计算公式，然后对公式的正确性进行验证。
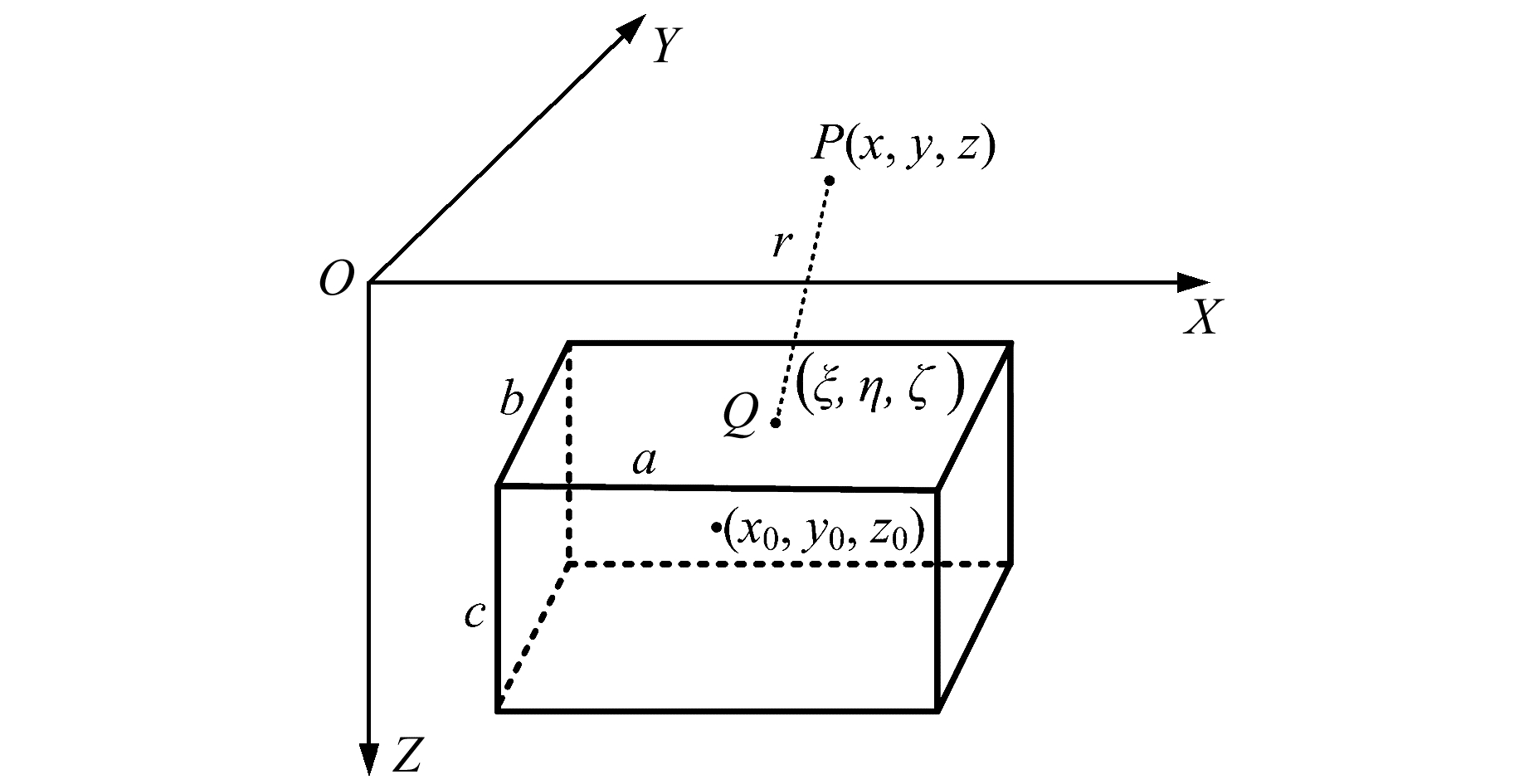
1 公式推导设有一个沿X轴方向长度为a、Y轴方向长度为b、Z轴方向长度为c的矩形棱柱体，其几何中心坐标为(x0, y0, z0)，如图 1所示。根据牛顿万有引力定律，可得密度均匀的矩形棱柱体在其外部P(x, y, z)点处的重力位[7]积分表达式为:
|
图 1 矩形棱柱体几何示意图 Fig. 1 Geometric sketch map of the right rectangular prism |
| $ U = {{G}}\rho \int_{{\xi _1}}^{{\xi _2}} {\int_{{\eta _1}}^{{\eta _2}} {\int_{{\zeta _1}}^{{\zeta _2}} {\frac{1}{r}} } } {\rm{d}}\xi {\rm{d}}\eta {\rm{d}}\zeta $ | (1) |
其中，ρ为密度，G=6.672×10-11m3/(kg·s2)为万有引力常数，r为观测点与体积元dξdηdζ之间的距离，即
| $ r = \sqrt {{{(\xi - x)}^2} + {{(\eta - y)}^2} + {{(\zeta - z)}^2}} $ | (2) |
重力二阶梯度是重力位的二阶导数，写成张量形式为：
| $ \left[ {\begin{array}{*{20}{c}} {{U_{xx}}}&{{U_{xy}}}&{{U_{xz}}}\\ {{U_{yx}}}&{{U_{yy}}}&{{U_{yz}}}\\ {{U_{zx}}}&{{U_{zy}}}&{{U_{zz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{\partial ^2}U}}{{\partial {x^2}}}}&{\frac{{{\partial ^2}U}}{{\partial x\partial y}}}&{\frac{{{\partial ^2}U}}{{\partial x\partial z}}}\\ {\frac{{{\partial ^2}U}}{{\partial y\partial x}}}&{\frac{{{\partial ^2}U}}{{\partial {y^2}}}}&{\frac{{{\partial ^2}U}}{{\partial y\partial z}}}\\ {\frac{{{\partial ^2}U}}{{\partial z\partial x}}}&{\frac{{{\partial ^2}U}}{{\partial z\partial y}}}&{\frac{{{\partial ^2}U}}{{\partial {z^2}}}} \end{array}} \right] $ | (3) |
根据众多重力梯度张量分量正演数值模拟和反演研究的文献资料[2-6]可得，矩形棱柱体不含解析奇点的重力二阶梯度张量解析公式为：
| $ \begin{array}{c} {U_{xx}} = G\rho \arctan \frac{{(\xi - x)(\eta - y)}}{{{{(\xi - x)}^2} + r(\zeta - z) + {{(\zeta - z)}^2}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\begin{array}{*{20}{c}} {{\xi _1}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. \end{array} $ | (4a) |
| $ \begin{array}{c} {U_{yy}} = G\rho \arctan \frac{{(\xi - x)(\eta - y)}}{{{{(\eta - y)}^2} + r(\zeta - z) + {{(\zeta - z)}^2}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. \end{array} $ | (4b) |
| $ {U_{zz}} = - G\rho \arctan \frac{{(\xi - x)(\eta - y)}}{{r(\zeta - z)}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (4c) |
| $ {U_{xy}} = G\rho \ln [r + (\zeta - z)]\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (4d) |
| $ {U_{xz}} = G\rho \ln [r + (\eta - y)]\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (4e) |
| $ {U_{yz}} = G\rho \ln [r + (\xi - x)]\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (4f) |
其中，ξ1=x0-a/2、ξ2=x0+a/2、η1=y0-b/2、η2=y0+b/2、ζ1=z0-c/2、ζ2=z0+c/2。
重力三阶梯度张量是重力位的三阶导数，并且通过分析张量的对称性可得，Uijk=Ujki=Ukij, i, j, k∈{x, y, z }。重力三阶梯度张量正演计算公式可由重力二阶梯度张量求导得到，也可对重力位三次求导积分得到。
由式(2)可得：
| $ \frac{{\partial r}}{{\partial x}} = - \frac{{\xi - x}}{r}, \frac{{\partial r}}{{\partial y}} = - \frac{{\eta - y}}{r}, \frac{{\partial r}}{{\partial z}} = - \frac{{\zeta - z}}{r} $ | (5) |
对于任意f(ξ－x, η－y, ζ－z)类型函数有：
| $ \frac{{\partial f}}{{\partial \xi }} = - \frac{{\partial f}}{{\partial x}}, \frac{{\partial f}}{{\partial \eta }} = - \frac{{\partial f}}{{\partial y}}, \frac{{\partial f}}{{\partial \zeta }} = - \frac{{\partial f}}{{\partial z}} $ | (6) |
并且
| $ \begin{array}{c} {U_{xxx}} = \frac{{\partial {U_{xx}}}}{{\partial x}} = \\ G\rho \frac{{(\eta - y)[{{(\xi - x)}^2} - r(\zeta - z)]}}{{r[{{(\xi - x)}^2} + {{(\zeta - z)}^2}][r + (\zeta - z)]}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. \end{array} $ | (7) |
| $ \begin{array}{c} {U_{yyy}} = \frac{{\partial {U_{yy}}}}{{\partial y}} = \\ G\rho \frac{{(\xi - x)[{{(\eta - y)}^2} - r(\zeta - z)]}}{{r[{{(\eta - y)}^2} + {{(\zeta - z)}^2}][r + (\zeta - z)]}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. \end{array} $ | (8) |
| $ \begin{array}{c} {U_{zzz}} = \frac{{\partial {U_{zz}}}}{{\partial z}} = \\ G\rho \frac{{(\xi - x)(\eta - y)[{r^2} + {{(\zeta - z)}^2}]}}{{r[{{(\xi - x)}^2} + {{(\zeta - z)}^2}][{{(\eta - y)}^2} + {{(\zeta - z)}^2}]}}\\ \;\;\;\;\;\;\;\;\;\;\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. \end{array} $ | (9) |
| $ \begin{array}{c} {U_{xyz}} = G\rho (\frac{\partial }{{\partial y}}(\frac{\partial }{{\partial x}}(\frac{1}{r}))){\rm{d}}\xi {\rm{d}}\eta {\rm{d}}\zeta = \\ - G\rho (\frac{\partial }{{\partial \eta }}(\frac{\partial }{{\partial \xi }}(\frac{1}{r}))){\rm{d}}\xi {\rm{d}}\eta {\rm{d}}\zeta = - G\rho \frac{1}{r}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. \end{array} $ | (10) |
由于Uxxy、Uxxz、Uxzz、Uyyx、Uyyz和Uyzz在形式上具有相似性，所以只要推出其中一个，然后再进行简单的变量替换便可获得其他几个张量分量的计算结果：
| $ {U_{xxy}} = G\rho \frac{{(\xi - x)(\zeta - z)}}{{[{{(\xi - x)}^2} + {{(\eta - y)}^2}]r}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (11) |
同理，可以导出：
| $ {U_{xxz}} = G\rho \frac{{(\xi - x)(\eta - y)}}{{[{{(\xi - x)}^2} + {{(\zeta - z)}^2}]r}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (12) |
| $ {U_{xzz}} = G\rho \frac{{(\eta - y)(\zeta - z)}}{{[{{(\zeta - z)}^2} + {{(\xi - x)}^2}]r}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (13) |
| $ {U_{yyx}} = G\rho \frac{{(\eta - y)(\zeta - z)}}{{[{{(\xi - x)}^2} + {{(\eta - y)}^2}]r}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (14) |
| $ {U_{yyz}} = G\rho \frac{{(\xi - x)(\eta - y)}}{{[{{(\eta - y)}^2} + {{(\zeta - z)}^2}]r}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (15) |
| $ {U_{yzz}} = G\rho \frac{{(\zeta - z)(\xi - x)}}{{[{{(\eta - y)}^2} + {{(\zeta - z)}^2}]r}}\left| {\begin{array}{*{20}{c}} {{\xi _2}}\\ {{\xi _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2}}\\ {{\eta _1}} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\zeta _2}}\\ {{\zeta _1}} \end{array}} \right. $ | (16) |
为了验证计算公式的正确性，首先采用重力二阶梯度张量正演计算公式计算理论模型的重力二阶梯度张量，再利用中心差分方法计算理论模型的重力三阶梯度张量异常，最后与本文计算结果进行对比与检验。
2.1 理论模型的重力三阶梯度张量分布如图 1所示，矩形棱柱体的长宽高分别为a=50 m、b=10 m、c=6 m，剩余密度为2.67 g/cm3，几何中心坐标为(125 m, 125 m, 50 m)，观测面为地面即z=0 m，地面测网大小250 m×250 m，网格间距为5 m×5 m，节点数共51×51=2 601个。利用式(7)~(16)，计算得到该矩形棱柱体模型的重力三阶梯度张量分布，如图 2所示。
|
(黑色矩形为矩形棱柱体模型的水平位置;蓝色实线为图3剖面的水平位置;1 pMKS=10-12 m-1s-2) 图 2 矩形棱柱体的重力三阶梯度张量分布 Fig. 2 Distribution maps of third-order gradient tensor of the gravitational potential caused by a right rectangular prism |
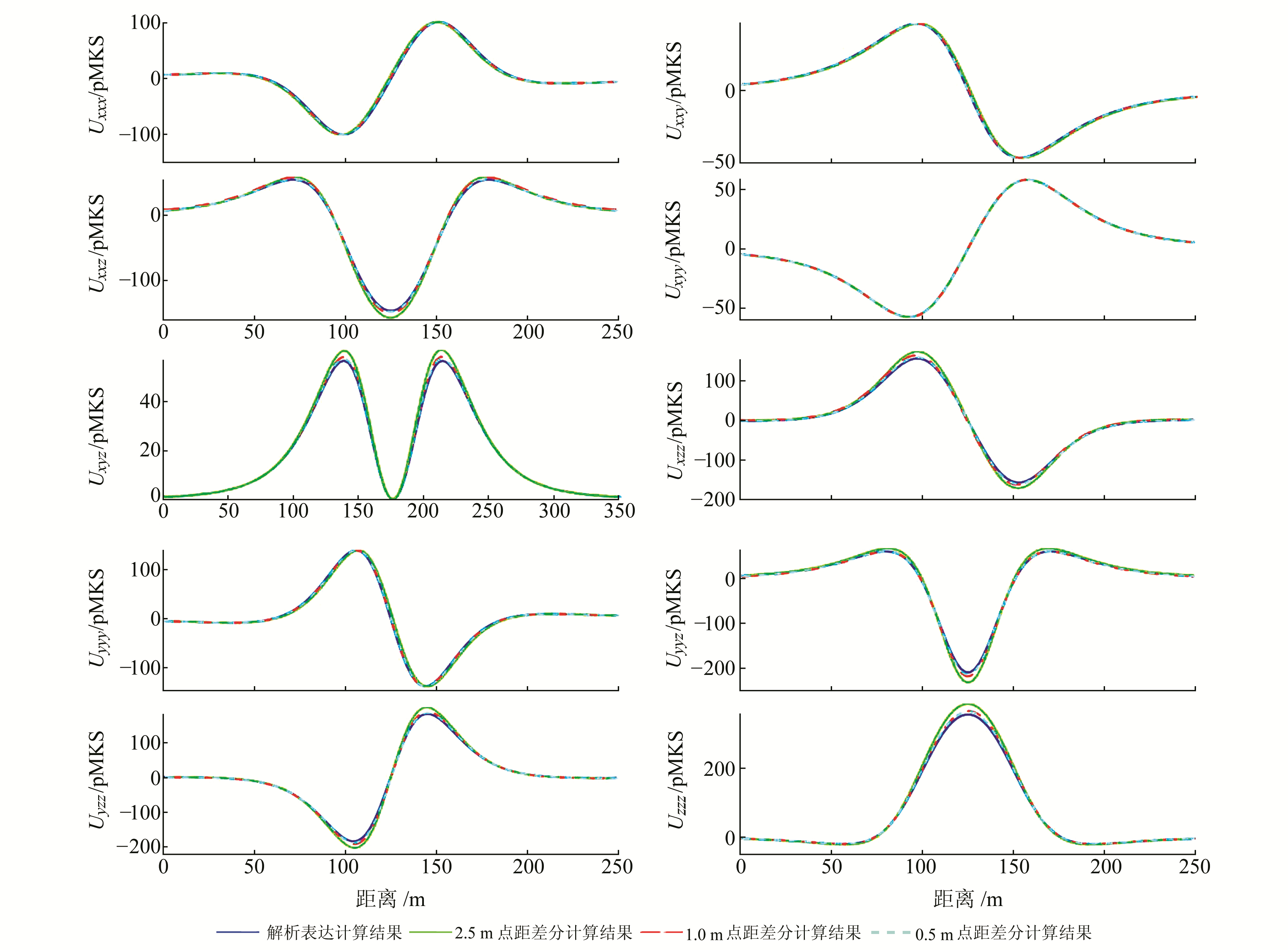
由导数的定义可知，重力三阶梯度张量可由其二阶梯度张量通过中心差分得到。故可通过与二阶梯度张量差分计算结果进行对比，来检验本文三阶张量正演计算公式的正确性。同时，选用3组点距(2.5 m、1 m与0.5 m)讨论不同点距的差分计算对差分计算结果的影响。图 3为图 2所示剖面(蓝色实线)的重力三阶梯度张量曲线以及不同点距的差分结果。从图 3可知，本文选用的3组差分计算结果都逼近重力三阶梯度张量计算结果，并且点距越小其计算精度越高，这证明了本文推导公式的正确性。
|
图 3 解析表达式与中心差分的计算结果对比 Fig. 3 Comparison between the calculating results by analytic expression and central differenc |
根据重力位(此处指扰动重力位)在场源外部空间满足拉普拉斯方程，重力三阶梯度张量的部分元素应该满足：Uxxx+Uxyy+Uxzz=0，Uxxy+Uyyy+Uyzz=0，Uxxz+Uyyz+Uzzz=0。利用此标准检验图 2所示计算结果，表明满足该3个方程，误差为0，这从另一方面证明本文推导公式的正确性。
3 结语鉴于矩形棱柱体在重力资料的正演模拟、数据处理、反演与解释之中的重要性，本文基于位场理论，经过推导得到矩形棱柱体重力位三阶梯度张量正演计算的解析公式；基于理论模型，对比解析公式与重力位二阶梯度张量中心差分的计算结果，并以计算结果是否满足拉普拉斯方程检验了推导公式的正确性。本文所得结果为重力位三阶梯度张量的仿真模拟、实测数据的处理与转换计算以及反演及解释提供了一种可行的计算方法。
参考文献
| [1] |
Li Y, Oldenburg D W. 3-D Inversion of Gravity Data[J]. Geophysics, 1998, 63(1): 109-119
(  0) |
| [2] |
Nagy D. The Gravitational Attraction of a Right Rectangular Prism[J]. Geophysics, 1996, 31(2): 362-371
( 0) |
| [3] |
Plouff D. Gravity and Magnetic Fields of Polygonal Prisms and Application to Magnetic Terrain Corrections[J]. Geophysics, 1976, 41(4): 727-741 DOI:10.1190/1.1440645
( 0) |
| [4] |
Pilkington M. Evaluating the Utility of Gravity Gradient Tensor Components[J]. Geophysics, 2014, 79(1): 1-14
( 0) |
| [5] |
郭志宏, 管志宁, 熊盛青. 长方体ΔT场及其梯度场无解析奇点理论表达式[J]. 地球物理学报, 2004, 47(6): 1 131-1 138 (Guo Zhihong, Guan Zhining, Xiong Shengqing. Cuboid ΔT and Its Gradient forward Theoretical Expressions without Analytic Odd Points[J]. Chinese Journal of Geophysics, 2004, 47(6): 1 131-1 138)
( 0) |
| [6] |
舒晴, 朱晓颖, 周坚鑫, 等. 矩形棱柱体重力梯度张量异常正演计算公式[J]. 物探与化探, 2015, 39(6): 1 217-1 222 (Shu Qing, Zhu Xiaoying, Zhou Jianxing, et al. Forward Modeling Expressions for Right Rectangular Prism with Constant Density[J]. Geophysical & Geochemical Exploration, 2015, 39(6): 1 217-1 222)
( 0) |
| [7] |
曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005 (Zeng Hualin. Gravity Field and Gravity Exploration[M]. Beijing: Geological Publishing House, 2005)
( 0) |
Forward Modeling Formulae for Third-Order Gradient Tensor of Gravitational Potential Caused by the Right Rectangular Prism
1. Hubei Subsurface Multi-scale Imaging Key Laboratory, Institute of Geophysics and Geomatics, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China;
2. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
2. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
Abstract: The forward modeling formulae for third-order gradient tensor of gravitational potential caused by the right rectangular prism is derived in this paper. Then, two different approaches are utilized to verify the obtained analytic expressions. One is the comparison between calculating results by our proposed formulae and by the central difference of second-order gradient tensor of the gravitational potential. The other is whether the computing results of the theoretic model meet the Laplace equation.
Key words:
third-order gradient tensor; gravitational potential; right rectangular prism; forward modeling; analytical expressions