2. 中国科学院南海海洋研究所边缘海与大洋地质重点实验室,广州市新港西路164号,510301;
3. 中国科学院大学,北京市玉泉路19号,100049
地震层析成像能够以图像的形式直观清晰地显示地球内部的精细结构和局部不均匀性,因而被广泛应用于地球内部物理和地球动力学、能源勘探开发、工程和灾害地质等领域[1]。但由于实际观测数据通常是不完备的,加之反演目标函数强烈的非线性,使得地震速度反演具有严重的非唯一性。地球物理联合反演通过综合多种信息约束可以有效降低多解性,改善数据不完备部位的成像质量[2]。地震-重力联合反演约束方法分为物性约束和结构约束[3],物性约束常因波速-密度存在较大散布其适用范围受到限制,而传统的简单结构约束方法要求有一个先验的地质模型。本文以南台湾海峡的应用为例,介绍近年来出现的交叉梯度结构约束法的原理、实现途径及应用效果。结果表明,添加重力场信息进行联合反演可以显著降低常规地震层析成像解的多解性,而交叉梯度结构约束是在大范围内使模型能保持较高分辨率的关键。
1 重力数据约束的地震层析成像 1.1 地震层析成像在实际应用中的困难利用广角地震资料中震相简单明确的初至波走时信息,采用层析成像方法反演沉积层上地壳速度结构对构造演化研究有重要意义[4],但必须注意层析成像的分辨能力主要依赖于射线密度及其方位角分布[5],因此使用地表激发接收的地震走时数据反演地下速度结构本身是一个病态的问题[6]。在实际应用中常常会遇到以下困难:
1) 地震观测系统往往受到各种限制,地震射线在模型空间某些区域难以满足空间采样要求;
2) 成功应用初至波层析成像的前提是拾取到准确可靠的初至走时信息,但在部分地区地震数据信噪比较低,难以拾取到可靠的初至;
3) 传统的初至波层析射线追踪算法存在明显的不足,例如在速度剧烈变化的情况下,因遵守费马原理,射线路径趋向于沿高速体传播,因此对低速异常体的分辨欠佳[7]。
因此,在实际数据集不完备、地下结构复杂的情况下反演的多解性较为严重,制约了初至走时层析成像的应用效果。
1.2 地震-重力联合反演的理论框架地震与非地震数据联合反演可在一定程度上弥补地震方法的缺陷,对地震速度反演加以约束,进而降低其多解性。对于多域的联合反演,目标函数的组成分为3个部分:数据项、正则化项和约束项[8]:
| $ \begin{array}{l} \;\;\;\mathit{\Phi }\left( {\mathop m \nolimits} \right) = \mathop \sum \limits_{\mathop i\nolimits} {\alpha _{\mathop i\nolimits} }{\mathit{W}_{{\mathop{ d}\nolimits} , i}}\left( {{{\mathop{ g}\nolimits} _{\mathop i\nolimits} }\left( {{{\mathop{ m}\nolimits} _{\mathop i\nolimits} }} \right) - {{\mathop{ d}\nolimits} _{\mathop i\nolimits} }} \right){{\mathop{ P}\nolimits} _i} + \\ \mathop \sum \limits_{\mathop i\nolimits} {\alpha _{\mathop i\nolimits} }\mathop \smallint \limits_{{{\mathop{ V}\nolimits} _{\mathop i\nolimits} }}^{} {\mathit{\Gamma }_{\mathop i\nolimits} }\left( {{{\mathop{ m}\nolimits} _{\mathop i\nolimits} } - {{\mathop{ m}\nolimits} _{{\rm{pri}}\mathit{\boldsymbol{, }}{\mathop i\nolimits} }}} \right){\rm{d}}{\mathop{ v}\nolimits} + \mathop \sum \limits_{\mathop j\nolimits} {\beta _{\mathop j\nolimits} }\mathop \smallint \limits_{{{\mathop{ U}\nolimits} _{\mathop j\nolimits} }}^{} {{{\mathit{\Psi } }}_j}\mathit{\boldsymbol{(}}{\mathop{ m}\nolimits} \mathit{\boldsymbol{)}}{\rm{d}}{\mathop{ v}\nolimits} \end{array} $ | (1) |
式中,i、j分别表示第i个数据域、第j个约束关系;mi与mpri, i分别表示第i个数据域的模型与先验模型;gi(mi)和di分别表示第i个数据域的计算数据与观测数据;W d, i为数据加权矩阵;P为误差泛函范数;α、β分别为数据项与约束项的加权系数;U、V分别为需要约束的空间区域和模型空间区域,Γ和Ψ分别为正则化函数和各模型物理量间的约束函数。
基于岩石密度与速度之间有较好的对应关系,可以在地震层析反演过程中加入地震走时与重力异常之间的约束项,提高反演所得速度模型的可靠性。在目标函数中,第一项代表每个数据域中模型正演数据与观测数据的残差的Pi范数之和,地震数据中选择初至走时,正演算法为有限差分法解程函方程;重力数据中选择重力异常残差,正演算法为空间域解法。第二项中正则化函数选择模型的一阶导数的2-范数。第三项约束函数最为关键,一般有两类:各模型间的物性经验关系约束和不同模型间的地质构造形态约束。对于大尺度如地壳结构模型的反演,受岩石不均匀性的影响较小[9],因此物性约束获得了较多成功的应用。
1.3 结构约束和交叉梯度算子物性约束的主要缺点是在结合地球物理数据生成综合模型时,忽略了岩石物性关系的不确定性。一方面,基于物性约束的方法需要准确的岩石物性特征,但对于初期石油勘探和海洋区域地质调查,很难获得大量的实测岩石物理参数用于统计,而不准确的经验公式会导致反演结果扭曲,在较大的勘探范围使用一个经验公式也是不合理的。另一方面,同一种岩石在不同构造单元、不同深度,波速-密度的关系也会发生变化,物性约束无法适应这种岩性的变化,从而限制了反演解的可靠性和分辨率。
结构约束的最大难点是从数学上定义构造共性以及将其用于构建目标函数。构造地球物理模型最简化的方法是利用一组具有确定边界的有限地质体,尽管该方法已得到较多应用,但其缺点是需要一个准确的先验地质模型,因此无法同时反演密度和构造(界面)。2004年,Gallardo等[10]提出交叉梯度,并将这种构造约束方法引入地震-电法联合反演中:用一个叉乘算子比较两个模型的空间梯度矢量方向,当两个梯度矢量成一直线时,交叉梯度为零:
| $ {\mathit{\Psi } _x}(x, y, z) = \nabla {m_r}(x, y, z) \times \nabla {m_s}(x, y, z) $ | (2) |
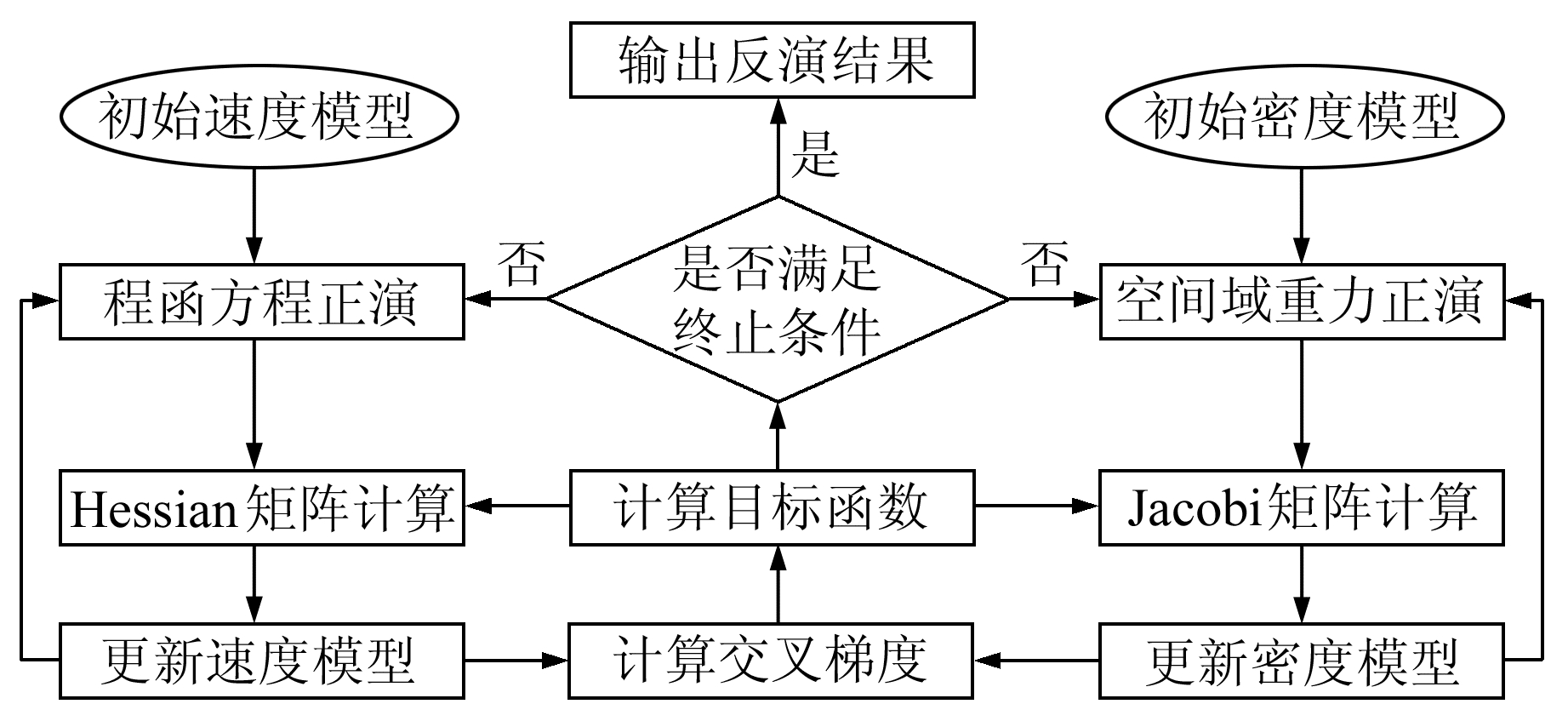
式中,左端为交叉梯度函数,右端的两项分别为两个模型的梯度算子,对于地震-重力联合反演可分别取密度的梯度与慢度的梯度。交叉梯度函数可作为一个约束条件,校验两个多维模型几何特征的相似性,提高了适应不同地质环境的特殊性的能力[11-12],因此近年来得到广泛关注。本文同时使用物性约束和结构约束构建统一的目标函数,实现重力数据约束的地震层析成像(图 1),以达到利用重力异常信息改善地震成像效果的目的。
|
图 1 重力数据约束的地震层析成像流程 Fig. 1 Flowchart of the seismic tomography constrained by gravity data |
为研究台湾海峡南部的地质构造组合形态,福建省地震局2015年在台湾海峡南部海域采集了HX-13地震探测剖面[13],该剖面跨越漳州-高雄断裂,南段经过澎湖-北港隆起,北段可能伸入九龙江凹陷(图 2)。该剖面使用大容量气枪震源激发,炮点距200 m,炮点数1 259个,信号接收使用27台MiniOBS海底地震仪,其中成功回收且记录正常的为22台。地震数据总体质量较好,但钻井和多道地震资料显示,该区在始新世和中新世发生了强烈的岩浆活动,新近纪沉积中广泛发育平板状、刺锥状、块状火成岩,形态复杂多变,在部分地区突露至海底[14]。由于火成岩密度和波速与围岩差异较大,产生的速度倒转、隐蔽层以及剧烈的横向速度变化使得部分区域(桩号160~190 km处)识别连续的折射初至较为困难(图 3(a))。首先使用有限差分法进行程函方程正演,用最速下降法反演得到沉积层上地壳速度结构模型(图 3(c)),该模型中缺乏射线覆盖的区域(图 3(b))速度结构可信度较低。

|
图 2 台湾海峡地质构造背景 Fig. 2 Geological structure map of Taiwan strait |

|
图 3 地震走时和反演结果 Fig. 3 Seismic travel-time and the inversion result |
沿测线的重力数据由台湾海峡船测空间重力异常数据网格插值得到;台湾海峡西南部水深变化平缓,在30~70 m之间,作布格改正得到布格重力异常;最后移去区域重力场,得到沉积层引起的重力异常(图 4(a))。

|
图 4 剖面重力异常和初始密度模型 Fig. 4 The initial density model and the distribution of gravity anomaly along the profile |
对于沉积岩石,Gardner等[15]给出了速度模型和密度模型之间的经验关系:
| $ \rho = 0.31 \cdot {V_p}0.25 $ | (3) |
用式(3)(或称Gardner公式)将单纯地震层析反演的速度模型转化为密度模型(图 4(b)),计算其重力异常,并与实测重力数据进行比较。对比重力异常和初始速度/密度模型可以发现,重力异常曲线与基底面起伏高度相关,在大部分区域吻合得很好,说明重力异常是基底面以上沉积层速度结构的反映,同时也验证了波速-密度公式在研究区大体适用。但在桩号160~190 km处,计算重力异常和实测重力异常完全不符,这正是地震走时数据缺失的部位,说明此处由于缺少可靠的初至信息,地震射线密度不足,导致速度模型严重偏离地下实际情况。
准确可靠的波速-密度关系对于地震-重力联合反演非常关键。必须注意的是,研究区内沉积岩石符合Gardner公式,但可能分布有基性火成岩、致密灰岩等非Gardner体,且其产状、岩性复杂多变,这是在该区应用地震-重力联合反演的困难所在,也是使用交叉梯度约束的主要考量。
3 实际资料的处理及效果分析 3.1 反演流程及参数以单纯走时反演得到的速度模型和Gardner公式转换的密度模型作为初始模型,使用§1所述的联合反演方法同步拟合地震走时和重力异常数据,并匹配波速-密度关系和构造形态约束。由于相对权比的数值大小反映模型对不同观测量的拟合程度[16],为充分利用重力数据对地层密度的响应,联合反演迭代首先对数据项取较大的权重,进而逐步调整数据项与约束项的权比;数据项中原始地震资料品质较好的部位赋以走时残差较大的权重,地震资料品质较差即模型中地震射线覆盖不足的部位赋以重力异常残差较大的权重;考虑到测区可能存在玄武岩、灰岩等非Gardner体,参考东海陆架盆地的岩石密度资料[17]将Gardner公式和交叉梯度的权比取为13 :7。经过7轮迭代,目标函数值稳定收敛到极小值,此时地震走时拟合均方差减小到56 ms,重力异常拟合均方差减小到1.6 mGal,达到了综合地震走时与重力异常信息同时反演物性与构造的目的。
3.2 反演结果分析联合反演得到的最终速度模型、密度模型和Gardner公式偏离度分布如图 5所示。可见,输出的速度模型和密度模型具有较高的结构相似性,在Gardner公式偏离度分布图上沉积层和基底的差异较为显著,由此可直观、准确地识别基底面形态;而Gardner公式偏离度正值较少表明可能存在的基性火成岩多为薄层状的侵入相,厚度小于走时反演的分辨率。与常规走时反演的初始模型相比,在有较多地震射线覆盖的区域大尺度的构造形态基本一致,不同的是初始模型上存在较多由于空间采样过度产生的虚假结构,而在输出模型中这些虚假结构消失了,说明联合反演更为稳定。在未能拾取到可靠初至即射线覆盖严重不足的部位输出模型较初始模型有了较大改善,表现为由密度模型计算的重力异常值与观测值较为接近。模型中桩号118 km附近有一大型台阶对应漳州-高雄断裂,基底面错动约800 m。单纯使用地震数据反演得到的模型在有效走时数据缺失的部位(桩号160~190 km)出现了凹陷的构造假象,而添加重力数据作为约束进行地震-重力联合反演的模型正确恢复了基底面缓慢抬升的形态,从而确定HX-13剖面在九龙江凹陷西缘之外。

|
图 5 地震-重力同步联合反演结果 Fig. 5 The results of the seismic-gravity simultaneous joint inversion |
由于岩石的地震波速和密度通常具有良好的对应关系,重力与地震数据联合反演对于改进建模具有重要价值,一是约束地震反演过程,降低多解性;二是在地震反演的垂向分层结构基础上对缺少射线覆盖的区域进行横向延伸,提高水平方向的分辨能力。在台湾海峡南部的应用中,重力数据为地震速度反演提供冗余的信息,有效降低了反演的多解性,改善了无地震射线覆盖部位的不确定性,正确恢复了地震走时数据缺失部位的构造图像,表明该方法可在很大程度上改善单纯使用地震数据得到的模型。
交叉梯度结构约束寻求不同物理参数模型在结构上的相似性,能够适应岩性复杂多变的应用环境,在勘探范围较大的情况下保持较高的分辨率,较物性约束更适用于初期面积普查以及后期的深层勘探以及海洋区域地质调查。本文通过在地震层析反演的目标函数中加入物性和结构约束项,在联合反演的框架下同时反演地震数据和重力数据,改善了数据不完备区域解的质量,有助于提高地震层析成像的分辨率。
致谢: 国家海洋局第二海洋研究所吴招才博士提供部分台湾海峡的船测空间重力异常数据,地震数据采集工作得到福建省海洋研究所“延平2号”科考船的支持和配合,在此一并致谢。
| [1] |
杨文采. 应用地震层析成像[M]. 北京: 地质出版社, 1993 (Yang Wencai. Applied Seismic Tomography[M]. Beijing: Geological Pablishing House, 1993)
(  0) 0) |
| [2] |
王乐洋, 许才军. 等式约束反演与联合反演的对比研究[J]. 大地测量与地球动力学, 2009, 29(1): 73-78 (Wang Leyang, Xu Caijun. Comparative Research on Equality Constraint Inversion and Joint Inversion[J]. Journal of Geodesy and Geodynamics, 2009, 29(1): 73-78)
(  0) 0) |
| [3] |
吴健生, 高德章, 刘晨光, 等. 海域深部结构重、磁、震联合反演和综合解释[M]. 上海: 同济大学出版社, 2016 (Wu Jiansheng, Gao Dezhang, Liu Chenguang, et al. Joint Inversion and Integrated Interpretation for Deep Offshore Structure with Gravity, Magnetic and Seismic Data[M]. Shanghai: Tongji University Press, 2016)
(  0) 0) |
| [4] |
王笋, 谢志招, 张艺峰, 等. 晋江外海沉积层上地壳速度结构的二维层析成像[J]. 地球物理学进展, 2015, 30(1): 106-110 (Wang Sun, Xie Zhizhao, Zhang Yifeng, et al. 2D Tomography of Velocity Structure of the Sediment and Upper Crust off the Coast of Jinjiang[J]. Progress in Geophysics, 2015, 30(1): 106-110)
(  0) 0) |
| [5] |
李贞, 郭飚, 刘启元, 等. 地震层析成像中模型参数化研究进展[J]. 地球物理学进展, 2015, 30(4): 1 616-1 624 (Li Zhen, Guo Biao, Liu Qiyuan, et al. Parameterization in Seismic Tomography[J]. Progress in Geophysics, 2015, 30(4): 1 616-1 624)
(  0) 0) |
| [6] |
成谷, 马在田, 张宝金, 等. 地震层析成像中存在的主要问题及应对策略[J]. 地球物理学进展, 2003, 18(3): 512-518 (Cheng Gu, Ma Zaitian, Zhang Baojin, et al. Primary Problems and According Strategies in Seismic Tomography[J]. Progress in Geophysics, 2003, 18(3): 512-518 DOI:10.3969/j.issn.1004-2903.2003.03.029)
(  0) 0) |
| [7] |
Median E, Lovatini A, Andreasi F G, et al. Simultaneous Joint Inversion of 3D Seismic and Magnetotelluric Data from the Walker Ridge[J]. First Break, 2012, 30(4): 85-88
(  0) 0) |
| [8] |
Stefano M D, Andreasi F G, Re S, et al. Multiple-Domain, Simultaneous Joint Inversion of Geophysical Data with Application to Subsalt Imaging[J]. Geophysics, 2011, 76(3): 69-80
(  0) 0) |
| [9] |
Smithson S B, Wenzel F, Ganchin Y V, et al. Seismic Results at Kola and KTB Deep Scientific Boreholes:Velocities, Reflections, Fluids, and Crustal Composition[J]. Tectonophysics, 2000, 329: 301-317 DOI:10.1016/S0040-1951(00)00200-6
(  0) 0) |
| [10] |
Gallardo L A, Meju M A. Joint Two-Dimensional DC Resistivity and Seismic Travel Time Inversion with Cross-Gradients Constraints[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B3): B03311
(  0) 0) |
| [11] |
Colombo D, Mantovani M, Sfolciaghi M, et al. Near Surface Solution in South Rub Al-Khali, Saudi Arabia Applying Seismic-Gravity Joint Inversion and Redatuming[J]. First Break, 2010, 28(2): 77-84
(  0) 0) |
| [12] |
Tartaras E, Masnaghetti A, Lovatini S, et al. Multi-Property Earth Model Building through Data Integration for Improved Subsurface Imaging[J]. First Break, 2011, 29(4): 83-88
(  0) 0) |
| [13] |
王笋, 丘学林, 方伟华, 等. 台湾海峡西南部的海陆联合深地震探测资料特点与处理对策[J]. 热带海洋学报, 2018, 37(2): 92-99 (Wang Sun, Qiu Xuelin, Fang Weihua, et al. Features of the Onshore-Offshore Seismic Data in Southwest Taiwan Strait and Some Processing Countermeasures[J]. Journal of Tropical Oceanography, 2018, 37(2): 92-99)
(  0) 0) |
| [14] |
钱星, 张莉, 徐立明, 等. 台湾海峡盆地九龙江凹陷火成岩发育特征及其油气地质意义[J]. 海洋地质与第四纪地质, 2015, 35(5): 111-116 (Qian Xing, Zhang Li, Xu Liming, et al. Igneous Rocks in Jiulongjiang SAG of Taiwan Strait Basin and Implications for Petroleum Geology[J]. Marine Geology & Quaternary Geology, 2015, 35(5): 111-116)
(  0) 0) |
| [15] |
Gardner G H F, Gardner L W, Gregory A R. Formation Velocity and Density-The Diagnostic Basics for Stratigraphic Traps[J]. Geophysics, 1974, 39(6): 770-780 DOI:10.1190/1.1440465
(  0) 0) |
| [16] |
张俊, 独知行, 杜宁, 等. 联合反演模型中相对权比的约束反演[J]. 大地测量与地球动力学, 2015, 35(4): 600-603 (Zhang Jun, Du Zhixing, Du Ning, et al. A Constraint Method to Determine Relative Weight Ratio Factors in Joint Inversion[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 600-603)
(  0) 0) |
| [17] |
高德章. 东海陆架盆地岩石密度与磁性[J]. 上海地质, 1995, 54(2): 38-45 (Gao Dezhang. Density and Magnetic of Rocks in the East Sea Shelf Basin[J]. Shanghai Geology, 1995, 54(2): 38-45)
(  0) 0) |
2. Key Laboratory of Ocean and Marginal Sea Geology, South China Sea Institute of Oceanology, CAS, 164 Xingangxi Road, Guangzhou 510301, China;
3. University of Chinese Academy of Sciences, 19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39

