2. 中国地震局地震研究所地震大地测量重点实验室,武汉市洪山侧路40号,430071
多面函数拟合法由Hardy[1]提出并用于地壳垂直形变分析,其理论基础是:任一光滑的数学表面可以用一系列规则的数学表面的总和以任意精度逼近。该方法以其简洁、精度高、不需先验约束信息等优点在测量领域得到广泛应用,国内外学者对该方法进行了大量研究和推广[2-6]。该方法的应用有3个关键问题:核函数选择、节点选取和平滑系数的取值。核函数选择和节点选取已有成熟简便的方法[3-4],平滑系数的取值一直没有得到很好的解决,这在一定程度上影响了多面函数拟合法的应用和推广。
本文分析平滑系数的数学含义及其作用,提出基于Tikhonov正则化的改进多面函数模型,引入正则化替代平滑系数,明确了正则化系数的作用和对模型的影响,给出基于泛化误差极小化原则的取值方法,并通过实例分析改进模型相对于原模型的优势。
1 平滑系数的数学意义分析设有m个已测点,S(x, y)为点(x, y)上的观测值,多面函数模型表示为:
| $ S\left( {x, y} \right) = \sum\limits_{j = 1}^n {{\alpha _j}\theta \left( {x, y;{x_j}, {y_j}} \right)} $ | (1) |
式中,n为节点数,要求n≤m,α为待定系数,θ(x, y; xj, yj)为核函数。
核函数的一般形式为:
| $ \theta \left( {x, y;{x_j}, {y_j}} \right) = {\left[ {{{\left( {x - {x_j}} \right)}^2} + {{\left( {y - {y_j}} \right)}^2} + {\delta ^2}} \right]^\beta } $ | (2) |
式中,δ2为平滑系数,β一般取0.5或1。注意到d2=(x-xj)2+(y-yj)2是平面两点距离的平方,核函数θ实际上是点(x, y)到节点(xj, yj)的距离d的函数。
对于平滑系数δ2,该因子可以略微改变核函数曲线的形状,因此Hardy[1]认为,δ2具有平滑曲线的效果,但是对于其具体原理和取值方法没有明确的结论。国内引进多面函数法后,学者们对平滑系数的取值作了大量研究,认为平滑系数合适的取值能略微提高模型的稳定性和精度,并提出一些经验性的取值范围[3-4, 6],但是对于其数学机制尚未作出完善的解释。目前,国内学者应用多面函数模型时,或者令δ2=0,或者按前人的模型取1~10之间的随机数[5, 7]。
用矩阵的形式描述多面函数模型,即
| $ {\mathit{\boldsymbol{S}}}= {\mathit{\boldsymbol{\theta}}}{\mathit{\boldsymbol{\alpha}}} $ | (3) |
根据正规方程可得其待定参数:
| $ \mathit{\boldsymbol{\alpha }} = {{\rm{(}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{\theta }}{\rm{)}}^{ - 1}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{S}} $ | (4) |
式中,θn×m为核函数矩阵,上述步骤求解的关键是对方阵(θTθ)n×n求逆。一个方阵必须是非奇异矩阵(满秩矩阵)才能进行求逆操作,否则方程无法得到唯一解,因此,方阵(θTθ)n×n的非奇异性决定了多面函数模型解的唯一性。
方阵(θTθ)n×n要满足非奇异,变量之间不能存在完全相关性。因此,首先核函数个数n必须不大于数据点个数m。当δ2=0时,核函数θ与节点距离d线性相关,当节点相对数据点对称分布或线性分布时,核函数矩阵θn×m中某两行或多行线性相关,方阵(θTθ)n×n为奇异矩阵,造成方程无法求解或多解;当δ2>0时,核函数曲线随δ2增大产生一定的扭曲,核函数θ与节点距离d不再线性相关,保证了方阵(θTθ)n×n非奇异,使方程能得到唯一解,增加了模型的稳定性。δ2越大,核函数曲线扭曲越大,与节点距离d的线性相关性越差,模型的稳定性越高。
然而,根据前人众多实际算例的经验,平滑系数δ2的取值并不是越大越好。随着δ2的增大,模型的拟合误差也在增大,δ2越大,对核函数曲线的扰动越大,拟合值的偏离也越大。定义偏差值为RSS,则:
| $ {\rm{Rss}} = {\sum\limits_{i = 1}^m {({S_i} - {{S'}_i})} ^2} = \sum\limits_{i = 1}^m {{{(\alpha \theta - \alpha \theta ')}^2}} $ | (5) |
取β=0.5,有:
| $ {\rm{Rss}} = \sum\limits_m {\sum\limits_n {\left[ {\alpha \times {{\left( {\sqrt {{d^2} + {\delta ^2}} - d} \right)}^2}} \right]} } $ | (6) |
令
| $ \frac{{\partial J}}{{\partial \delta }} = \frac{\delta }{{\sqrt {{d^2} + {\delta ^2}} }} = \frac{1}{{\sqrt {1 + \frac{{{d^2}}}{{{\delta ^2}}}} }} > 0 $ | (7) |
即J与δ2呈线性正相关,也即RSS随δ2的增大而指数增加。
综上所述,平滑系数δ2>0时,能保证方程得到唯一解,但模型的拟合误差也随着δ2的增大而增加。
2 引入Tikhonov正则化替代平滑系数希望寻找一种新的方法,在不显著增加拟合误差的情况下确保方程得到唯一解,以替代平滑系数的作用,规避其不确定性。
对于解不唯一的情况,一种解决办法是正则化方法[8],增加一些限制缩小解的范围求解病态问题。本文采用Tikhonov正则化法,该方法在经典最小二乘准则的基础上,通过引入正则化矩阵,加入参数向量范数最小的条件,解决解的病态问题,确保方程有唯一解[9]。
引入Tikhonov正则化,即在偏差函数后增加一个正则化项:
| $ {\rm{Rss}} = {\rm{Rs}}{{\rm{s}}_0} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\mathop \sum \limits_{j = 1}^n \alpha _j^2 $ | (8) |
式中,RSS0为原始的偏差值,后一项为正则化项,Γ称为Tikhonov矩阵。
通过求得最小的偏差函数min(RSS)确定未知参数,有:
| $ \frac{{\partial {\rm{RSS}}}}{{\partial \alpha }} = \frac{{\partial {\rm{RS}}{{\rm{S}}_0}}}{{\partial \alpha }} + 2{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{{\rm{T}}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \alpha }} = 0 $ | (9) |
由式(5)有:
| $ \frac{{\partial {\rm{RS}}{{\rm{S}}_0}}}{{\partial \alpha }} = 2{\mathit{\boldsymbol{\theta }}^{{\rm{T}}}}\left( {\mathit{\boldsymbol{S}}{\bf{ - }}\mathit{\boldsymbol{\theta \alpha }}} \right) $ | (10) |
代入式(9),得到:
| $ 2{\mathit{\boldsymbol{\theta }}^{{\rm{T}}}}\left( {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{\theta \alpha }}} \right) + 2{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{{\rm{T}}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \alpha }} = 0 $ | (11) |
进而求出待定参数:
| $ \mathit{\boldsymbol{\alpha }} = {\left( {{\mathit{\boldsymbol{\theta }}^{{\rm{T}}}}\mathit{\boldsymbol{\theta }} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{{\rm{T}}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} \right)^{ - 1}}{\mathit{\boldsymbol{\theta }}^{{\rm{T}}}}\mathit{\boldsymbol{S}} $ | (12) |
对比式(4)和式(12)可知,应用Tikhonov正则化法,计算时只需在方阵(θTθ)n×n后增加一个正则化项Γ T Γ。
取Γ =aIn,即单位矩阵的a倍,称为L2正则化[10]。L2正则化是最常见的正则化形式,在机器学习、统计数学等领域应用广泛[11-12]。L2正则化不仅能解决解的病态问题,而且能防止过拟合,提升模型的泛化能力[10]。
此时式(12)变为:
| $ \mathit{\boldsymbol{\alpha }} = {\left( {{\mathit{\boldsymbol{\theta }}^{{\rm{T}}}}\mathit{\boldsymbol{\theta }} + \lambda {\mathit{\boldsymbol{I}}_n}} \right)^{ - 1}}{\mathit{\boldsymbol{\theta }}^{{\rm{T}}}}\mathit{\boldsymbol{S}} $ | (13) |
式中,λ=a2为正则化系数,In为n阶单位矩阵。当λ>0时,由于增加了一个正则化项,方阵(θ T θ +λ In)必定满秩可逆,方程有唯一解,保证了模型的稳定性。考察其对偏差函数的影响
另外,引入Tikhonov正则化后,核函数个数n不能大于测点数m的约束条件不再必要。当n>m时,由于引入正则化项,方阵(θ T θ +λ In)仍可逆,模型仍能保证有唯一解。这意味着应用多面函数拟合法时核函数个数有了更多更优的选择,拟合的空间分辨率能够大大提升,同时在测点较少的情况下也能够应用多面函数模型进行拟合计算,拓宽了多面函数模型的应用范围。
综上,改进多面函数模型引入Tikhonov正则化替代平滑系数,能保证方程有唯一解,增加了模型的稳定性,对模型拟合精度的影响较小;同时,去除了核函数个数n的约束条件,拓宽了模型的空间分辨率和应用范围。
3 实例分析 3.1 正则化系数的确定为了确定改进模型的正则化系数及评估改进模型的效果,本文以GPS水平速度场拟合为例进行计算分析。选用中国大陆构造环境监测网络在川滇地区75个基准站2009~2011年相对于欧亚板块的水平速度数据(来自国家地震科学数据共享中心),其点位分布如图 1所示,将每个站点的水平速度分解为E方向和N方向两个垂直分量。

|
图 1 川滇地区站点在欧亚框架下的水平速度场 Fig. 1 Horizontal velocity field of the Sichuan-Yunnan sites under the Eurasian framework |
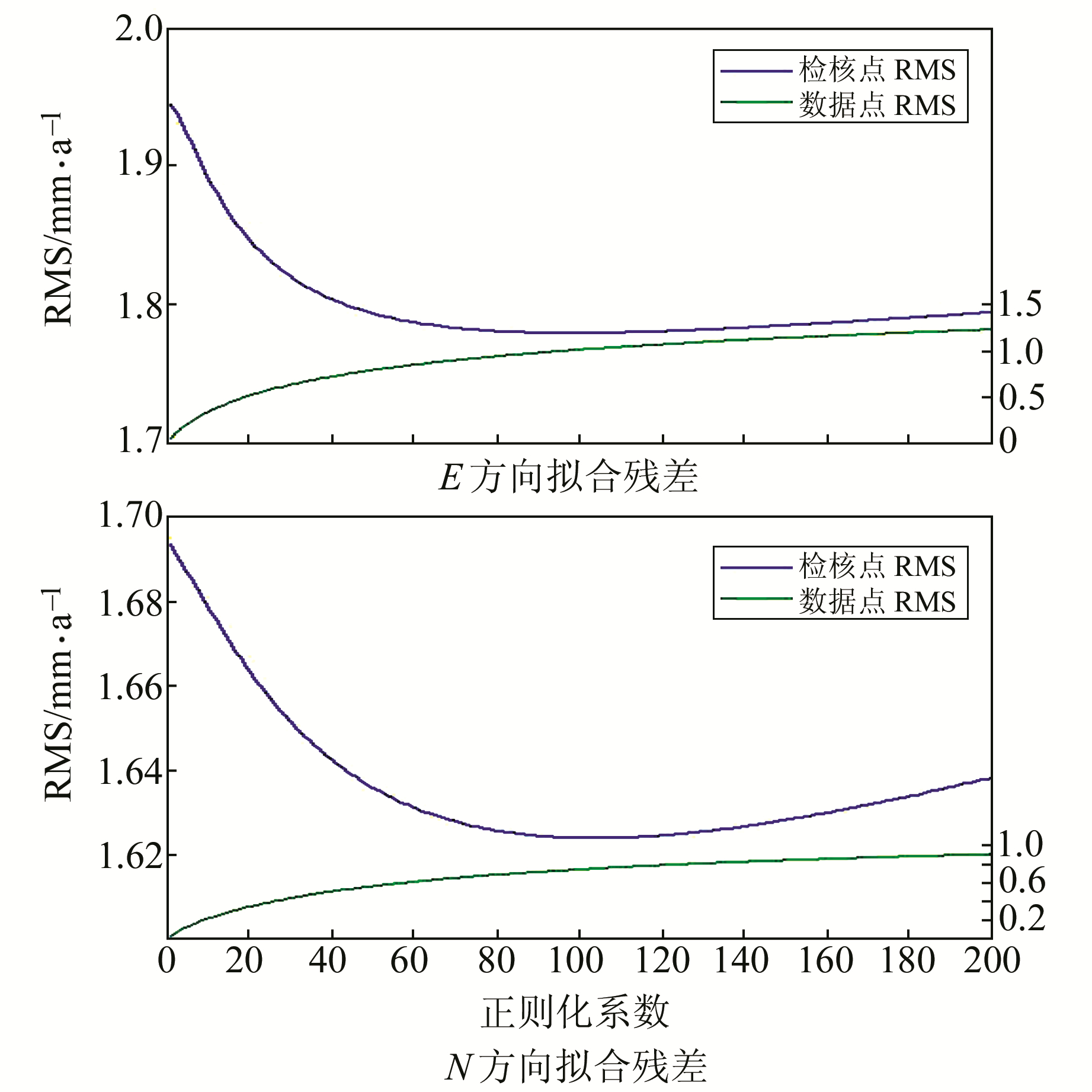
随机选取均匀分布的50个站点作为数据点,其余25个站点作为测试检核点。采用改进多面函数模型,取通用距离型核函数,核函数的幂次取0.5,以全部75个站点作为拟合节点,正则化系数从10开始以10为步长依次递增至200,分别计算数据点拟合残差RMS和检核点偏差RMS。数据点拟合残差反映模型的拟合精度,检核点偏差反映模型的泛化能力,即对未知数据的预测精度。
由图 2可知,数据点拟合残差RMS(Jtrain)随着正则化系数λ的增大而略有增加,与前文中正则化对偏差函数影响的讨论结果一致,而检核点偏差RMS (Jtest)在λ>0时是一条开口向上的类抛物线,存在全局最小值,在λ∈[10, 200]范围内,Jtrain<Jtest。表 1给出了改进多面函数模型试算精度统计结果(单位mm/a)。
|
图 2 不同正则化系数时的拟合残差RMS Fig. 2 Fitting residual RMS of different regularization coefficients |
|
|
表 1 改进多面函数模型试算精度统计 Tab. 1 Trial calculation accuracy statistics of refined method |
应用多面函数模型进行拟合计算时,希望平衡模型的拟合精度和泛化能力,不仅能够较精确地拟合数据点,也能较准确地预测未知数据,即模型拟合残差和检核点偏差均不太大。因Jtrain单调增加,而Jtest是一条存在全局最小值的类抛物线,且Jtrain<Jtest,因此可以根据泛化误差极小化原则确定正则化系数λ的取值,即以Jtest全局最小的拐点位置作为λ的取值。
由表 1可知,当λ=100时,E、N两方向Jtest最小,取100为改进模型正则化系数取值,此时模型拟合精度较高且泛化性能最好。同时,当正则化系数λ在40~200范围变化时,E方向Jtrain变化范围为1.779~1.804 mm/a,变化幅度为1.4%;N方向Jtrain变化范围为1.624~1.643 mm/a,变化幅度为1.2%。说明改进模型的未知点预测精度对正则化系数λ的取值变化敏感度较低,拟合效果比较稳定。
3.2 改进模型与原模型的比较采用相同的数据点和检核点,使用原多面函数模型对GPS水平速度场进行拟合,核函数的幂次同样取0.5,因多面函数模型核函数个数n不得大于数据点个数m,因此选择50个数据点作为拟合节点。与改进模型一样,以检核点偏差RMS(Jtest)最小化的方法确定平滑系数的取值。
经过试算,E方向平滑因子取10,N方向平滑因子取100时Jtest最小,数值结果见表 2(单位:mm/a)。
|
|
表 2 多面函数模型试算精度结果 Tab. 2 Multiquadric function method trial calculation accuracy results |
将多面函数模型的拟合结果与改进多面函数模型的拟合结果进行比较,结果见表 3(单位mm/a)。
|
|
表 3 两种模型的拟合精度比较 Tab. 3 Comparison of fitting accuracy of two models |
从表 3可见,改进多面函数模型在拟合GPS水平速度场时,数据点符合精度和检核点符合精度相对于原模型都有明显提高,表明改进模型的拟合精度和泛化能力均高于原模型,改善了拟合效果。
4 结语在多面函数模型实际应用过程中,平滑系数的取值一直没有得到很好的解决。本文在分析平滑系数的数学意义和作用后,提出引入Tikhonov正则化代替平滑系数的改进模型来解决上述问题。Tikhonov正则化法数学原理清晰,功能明确,同时去除了核函数个数的约束条件,拓宽了多面函数法的应用范围。
本文通过GPS水平速度场拟合的实例对改进模型进行验证,结果表明改进模型拟合效果稳定,数据点符合精度和检核点符合精度相较于原模型都有明显提高,表明改进模型的拟合精度和泛化能力均高于原模型,这进一步说明了改进模型的可行性和优越性。
| [1] |
Hardy R L.The Application of Multi-Quadric Equations and Point Mass Anomaly Models to Crustal Movement Studies[R].NOAA Technical Report, 1978
(  0) 0) |
| [2] |
Hardy R L. Hardy's Multiquadric-Biharmonic Method for Gravity Field Predictions Ⅱ[J]. Computers and Mathematics with Applications, 2001, 41(7): 1 043-1 048
(  0) 0) |
| [3] |
杨国华, 黄立人. 速率面拟合法中多面函数几个特性的初步数值研究[J]. 地壳形变与地震, 1990(4): 70-82 (Yang Guohua, Huang Liren. Preliminary Numerical Study on Several Characteristics of Multi-Faceted Functions in Rate Surface Fitting Method[J]. Crustal Deformation and Earthquake, 1990(4): 70-82)
(  0) 0) |
| [4] |
陶本藻, 姚宜斌. 基于多面核函数配置型模型的参数估计[J]. 武汉大学学报:信息科学版, 2003, 28(5): 547-550 (Tao Benzao, Yao Yibin. Parameter Estimation Based on Multi-Quadric Collocation Model[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 547-550)
(  0) 0) |
| [5] |
刘经南, 施闯, 姚宜斌, 等. 多面函数拟合法及其在建立中国地壳平面运动速度场模型中的应用研究[J]. 武汉大学学报:信息科学版, 2001, 26(6): 500-503 (Liu Jingnan, Shi Chuang, Yao Yibin, et al. Hardy Function Interpolation and Its Applications to the Establishment of Crustal Movement Speed Field[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6): 500-503)
(  0) 0) |
| [6] |
马洪滨, 董仲宇. 多面函数GPS水准高程拟合中光滑因子求定方法[J]. 东北大学学报:自然科学版, 2008(8): 1 176-1 178 (Ma Hongbin, Dong Zhongyu. A Method for Determining Smoothing Factor in GPS Level Height Fitting of Multi-Faceted Functions[J]. Journal of Northeastern University:Natural Science, 2008(8): 1 176-1 178)
(  0) 0) |
| [7] |
彭钊, 陈志遥, 吕品姬. 多面函数法在钻孔应变时序资料处理中的应用[J]. 中国地震, 2015, 31(2): 382-389 (Peng Zhao, Chen Zhiyao, Lü Pinji. Method of Multi-Kernel Function and Its Application in Borehole Strain Timing Data Processing[J]. Earthquake Research in China, 2015, 31(2): 382-389 DOI:10.3969/j.issn.1001-4683.2015.02.023)
(  0) 0) |
| [8] |
Neumaier A. Solving Ill-Conditioned and Singular Linear Systems:A Tutorial on Regularization[J]. SIAM Review, 1998, 40: 636-666 DOI:10.1137/S0036144597321909
(  0) 0) |
| [9] |
徐新禹, 李建成, 王正涛, 等. Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J]. 测绘学报, 2010, 39(5): 466-470 (Xu Xinyu, Li Jiancheng, Wang Zhengtao, et al. The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 466-470)
(  0) 0) |
| [10] |
Andrew Y N.Feature Selection, L1 vs.L2 Regularization, and Rotational Invariance[C].ACM, 2004
(  0) 0) |
| [11] |
Massini M, Fortunato M, Mancini S, et al. L2 Regularization for Learning Kernels[J]. Conference on Uncertainty in Artificial Intellige, 2012, 62(4): 109-116
(  0) 0) |
| [12] |
Fei H, Huan J.L2 Norm Regularized Feature Kernel Regression for Graph Data[C].18th ACM Conference on Information and Knowledge Management, 2009
(  0) 0) |
2. Key Laboratory of Earthquake Geodesy, Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China
 2019, Vol. 39
2019, Vol. 39

