2. 武汉大学测绘学院,武汉市珞喻路129号,430079
GNSS定向技术是利用GNSS观测手段来实时确定载体姿态的方法,已广泛应用于车辆、舰船和飞行器等动态载体的姿态测量中[1-2]。一般的GNSS载体定向中常采用双频测量型接收机,它具备高精度、高可靠性的优点,但是昂贵的价格和较大的体积限制了其普及。低成本GNSS接收机如瑞士u-blox公司的产品具有功耗低、体积小、集成度高等优点,针对其在高精度GNSS定位的研究越来越多。Takasu等[3]对低成本螺旋天线和u-blox接收机在RTK定位中的表现进行评估,指出天线质量是影响定位精度的主要因素;Odolinski等[4]实验对比发现,u-blox接收机在模糊度解算和定位表现上可以和测量型双频GPS接收机处于同一量级;Mongrédien等[5]基于u-blox接收机和差分改正信息实现短基线cm级的定位精度;Zuo等[6]使用u-blox接收机和测量型天线得到静态1.2 cm、动态2.4 cm的定位精度。但这些都是针对u-blox接收机在RTK定位方面的研究,鲜有文献对其高精度测姿的性能进行评估。姿态测量是GNSS应用的一个重要分支,基于低成本u-blox接收机的高精度姿态测量将具有广阔的应用市场和发展前景。为此,本文针对高精度GNSS定向应用,采用静态数据和车载动态数据,首先从信噪比、双差相位残差、双差伪距残差等方面对u-blox接收机的数据质量进行分析;之后分别使用u-blox与高精度测量型接收机进行GNSS定向解算,并评估低成本单频u-blox接收机在高精度定向中的实际应用效果,以期为后续基于低成本接收机的高精度姿态测量研究以及广大用户提供参考。
1 GNSS载体定向算法GNSS载体定向是通过在载体上架设2台信号接收天线,基于GNSS技术确定该基线向量在给定坐标系下的指向,其基线长度一般只有几米到几十米。因此定向算法的实质为GNSS短基线相对定位解算,通常采用双差观测模型,可以消除钟差、大气延迟误差以及卫星轨道误差等公共系统误差项。GNSS双差观测方程为:
| $ \begin{array}{l} P_{{\rm{AB}}}^{ij}{\rm{ = }}\rho _{{\rm{AB}}}^{ij} + \varepsilon _{{\rm{AB}}}^{ij}\\ L_{{\rm{AB}}}^{ij}{\rm{ = }}\rho _{{\rm{AB}}}^{ij} + \lambda N_{{\rm{AB}}}^{ij} + \xi _{{\rm{AB}}}^{ij} \end{array} $ | (1) |
式中,PABij和LABij分别为双差伪距观测值和载波相位观测值,εABij和ξABij为双差观测噪声,ρABij为双差的卫地几何距离,λ为载波波长,NABij为双差整周模糊度。
1.1 数据质量控制GNSS定向系统通常搭载在运动载体上,观测环境复杂多变,观测数据不可避免地存在周跳和粗差等异常,特别是对于低成本的u-blox接收机,粗差出现的频率明显高于测量型接收机。为了实现高精度定位和定向,一般需要在数据预处理和参数估计两个层面对上述异常进行探测和质量控制。在数据预处理层面,可采用多维粗差探测方法识别粗差;在参数估计层面,可使用抗差估计的方法,如抗差卡尔曼滤波或抗差最小二乘。本文采用文献[7]中改进的IGGⅢ方法进行抗差估计,该方法可以改善未探测到的小周跳对滤波解算的影响,同时兼顾粗差的处理,能够显著提高模糊度固定率、定位精度和可靠性。
1.2 附有基线长度约束的CLAMBDA方法根据双差观测方程,按照最小二乘方法解算出模糊度浮点解
低成本u-blox接收机相比于测量型接收机具有明显的价格优势,但其硬件性能要劣于测量型GNSS接收机,导致观测数据的质量较差,例如卫星信号的信噪比较低、观测值精度较差、卫星失锁和观测数据缺失现象出现得更加频繁等。此外,u-blox接收机观测信道数有限,通常只能承载2个导航卫星系统的观测数据(本文选择GPS和BDS系统),且只能输出单频信号,无法在不同频率间构建组合观测值,不利于周跳探测和模糊度的解算。
因此,在使用低成本u-blox接收机之前,有必要对其数据质量进行初评。本文采用一组动态车载实验数据,从卫星信噪比、相位观测值精度和伪距观测值精度3个方面对u-blox接收机的数据质量进行分析。该组动态数据采集于2018-01-23 07:30~09:40,共2 h 10 min,数据采样间隔为1 s。实验车辆在武汉梁子湖大道上行驶,车上一前一后搭载2台Trimble Zephyr Model2天线,两天线间的基线长度为1.13 m,每台天线均通过功分器分别连接NovAtel ProPak6型接收机和u-blox M8P接收机。限于篇幅,本文仅使用前天线的观测数据进行质量分析。
2.1 信噪比分析信噪比(SNR)是指接收的载波信号强度与噪声强度的比值,它是衡量观测值质量的重要指标。一般来说其值越高则观测值的质量越好,但受限于硬件的性能,低成本u-blox接收机数据的信噪比通常要低于测量型接收机。将NovAtelProPak6接收机和u-blox接收机通过功分器连接同一台GNSS天线,则其观测数据的质量仅取决于接收机的表现。图 1给出NovAtel ProPak6和u-blox观测数据的信噪比随卫星高度角变化的情况,图 2给出信噪比的频率分布直方图。

|
图 1 NovAtel ProPak6和u-blox信噪比随卫星高度角变化图 Fig. 1 SNR against satellite elevation of NovAtel ProPak6 and u-blox |

|
图 2 信噪比频率分布直方图 Fig. 2 Frequency distribution histogram of SNR |
由图 1和图 2可以看出,随着卫星高度角的升高,SNR值逐渐增大并趋于稳定,其中NovAtel ProPak6接收机数据的信噪比主要分布在30~50 dB-Hz之间,低成本u-blox数据的信噪比主要分布在20~50 dB-Hz之间,且仅当卫星高度角低于15°时,u-blox有少部分数据的SNR值低于30 dB-Hz。除少数u-blox数据的SNR值低于30 dB-Hz外,两种接收机的信噪比分布情况基本相同。此外,无论是低成本u-blox接收机还是NovAtel ProPak6接收机,GPS系统的信噪比都整体略高于BDS系统。
2.2 双差相位残差分析在GNSS定向中采用的是双差观测模型,利用已知基线分量(零基线时分量都严格为零)可以反算出双差伪距残差εABij和双差相位残差ξABij:
| $ \begin{array}{l} \varepsilon _{{\rm{AB}}}^{ij} = P_{{\rm{AB}}}^{ij} - \rho _{{\rm{AB}}}^{ij}\\ \xi _{{\rm{AB}}}^{ij} = L_{{\rm{AB}}}^{ij} - \rho _{{\rm{AB}}}^{ij} - \lambda N_{{\rm{AB}}}^{ij} \end{array} $ | (2) |
式中,εABij和ξABij分别反映了伪距观测值和载波相位观测值的精度,其值越小则观测值的精度越高。
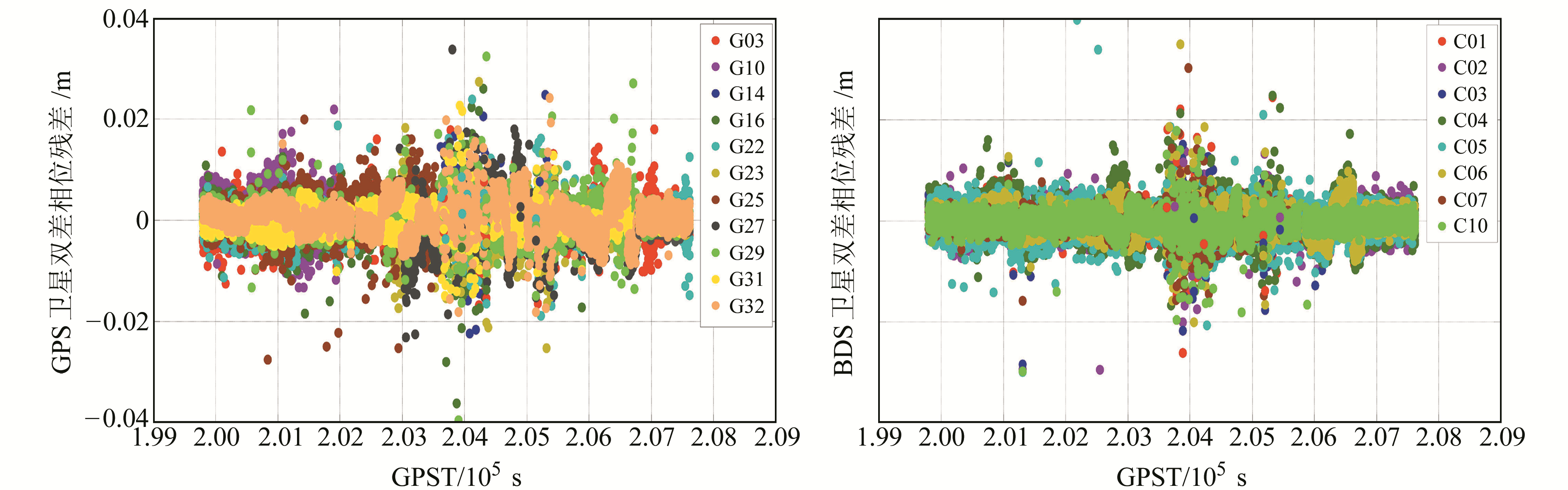
图 3分别绘出GPS和BDS所有卫星对的双差相位残差逐历元序列图(其中GPS系统使用高度角最高的G26卫星作为参考星,BDS系统使用高度角最高的C09卫星作为参考星,下同)。由图 3可以看出,GPS和BDS的双差相位残差基本都在2 cm(约0.1周)以内,统计其RMS值分别为1.35 cm和1.20 cm。考虑到测量型接收机NovAtel ProPak6的伪距精度在4~6 cm,相位精度在0.5~1 mm[10],可近似认为该双差残差反映的是u-blox观测值的精度。整体来看,低成本u-blox接收机的载波相位精度可以满足高精度定位和定向的需求。
|
图 3 GPS和BDS所有卫星对的双差相位残差 Fig. 3 Double-difference phase residuals of GPS and BDS satellites |
对于伪距观测值,根据式(2)可以反算出双差伪距残差,其值越小则说明伪距观测值的精度越高,模糊度的固定效率及可靠性也越高。这里仍使用前天线的NovAtel ProPak6接收机和u-blox接收机构成的零基线,分别绘出GPS和BDS所有卫星对的双差伪距残差序列图,如图 4所示。可以看出,GPS和BDS的双差伪距残差基本都在3 m以内,统计其RMS值分别为0.91 m和0.57 m,可以满足高精度定位定向的需求。

|
图 4 GPS和BDS所有卫星对的双差伪距残差 Fig. 4 Double-difference pseudorange residuals of GPS and BDS satellites |
为了分析比较低成本u-blox接收机和测量型接收机数据的定向精度,采用武汉大学测绘学院自主研制的GNSS高精度定位、测速和测姿软件KinPOS v2.0进行解算分析,该软件可以处理GPS+BDS的单/多频观测数据,实现前文所述的抗差估计和CLAMBDA解算模块,能够获得高精度的载体姿态信息。
采用一组静态短基线数据和一组动态车载实验数据,分别利用u-blox接收机和测量型接收机进行定向解算并统计精度。对于静态数据,采用静态模拟动态的方式进行解算,同时使用商用静态处理软件CGO解算得到基线分量以及基线长的参考值;对于动态数据,使用加拿大NovAtel公司发布的高精度事后动态处理软件GrafMov解算的结果作为参考值。
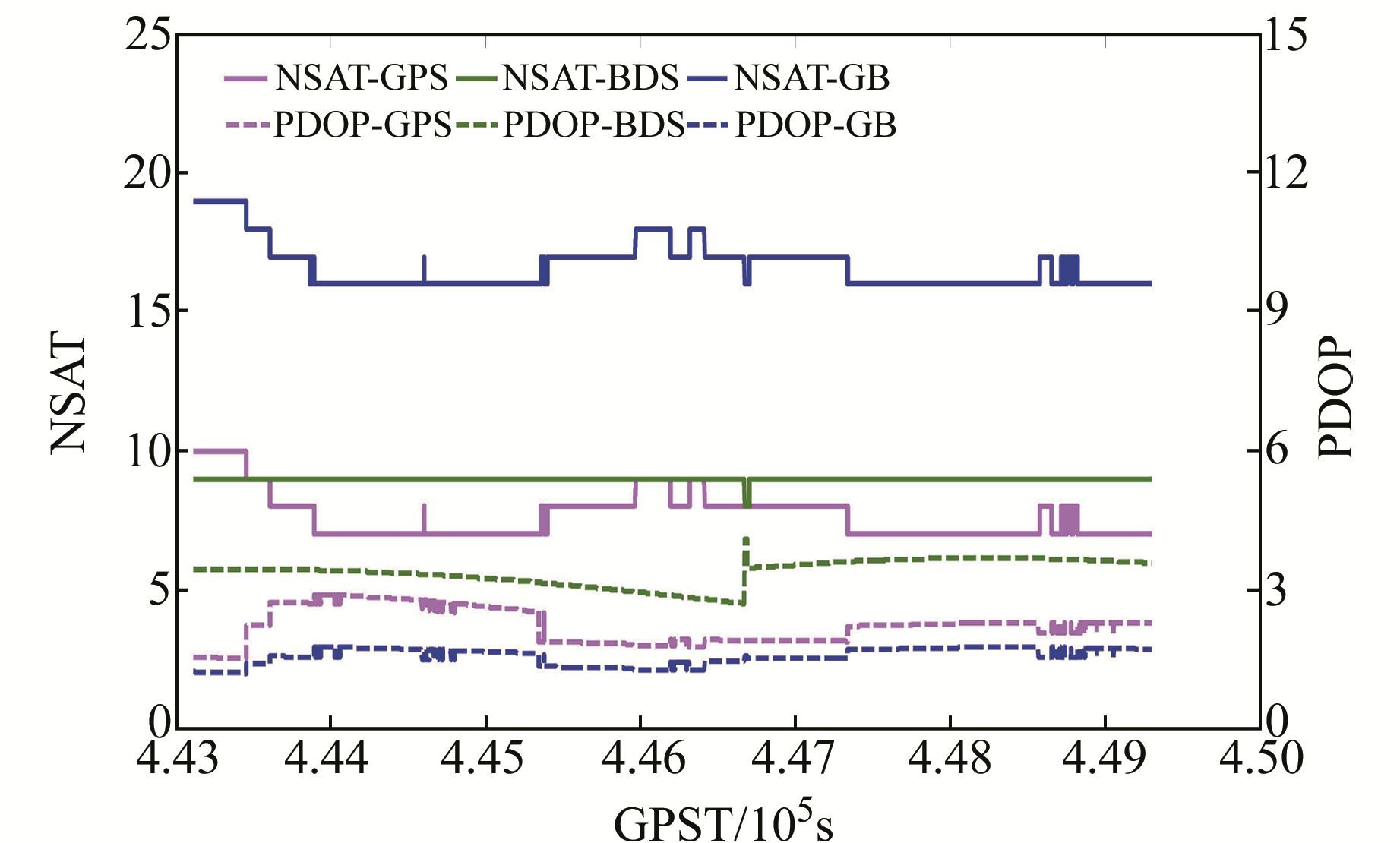
3.1 静态数据测试本组静态数据采集于2018-04-27 02:58~04:48,共1 h 50 min,数据采样间隔为1 s。基准站位于武汉大学教学实验大楼楼顶,天线为UniStrong UA91 3D扼流圈天线;流动站位于测绘学院楼顶,天线为Trimble Zephyr Model2。基准站和流动站均通过功分器分别连接NovAtel ProPak6接收机和低成本u-blox M8P接收机,2台天线间基线长90.48 m,截止高度角为10°。图 5给出了共视卫星数和DOP值序列图。
|
图 5 共视卫星数及DOP值 Fig. 5 Number of satellites in common and DOP |
分别使用2台NovAtel ProPak6接收机和2台u-blox接收机构成短基线,按照前文所述的静态模拟动态策略进行处理,为确保解算条件相同,NovAtel ProPak6仅使用GPS和BDS单频观测数据。将二者的姿态角解算结果与参考值作差,绘出其偏差序列,如图 6、图 7所示。统计基线向量和姿态角的解算精度,如表 1所示,其中航向角和俯仰角精度已归算至1 m长基线(下同)。

|
图 6 NovAtel ProPak6接收机姿态角解算结果偏差序列图 Fig. 6 Attitude angle bias resolved by NovAtel ProPak6 data |

|
图 7 u-blox接收机姿态角解算结果偏差序列图 Fig. 7 Attitude angle bias resolved by u-blox data |
|
|
表 1 静态实验NovAtel ProPak6和u-blox解算精度 Tab. 1 Resolving accuracy of NovAtel ProPak6 and u-blox in static experiment |
由图 6、图 7可以看出,NovAtel ProPak6和u-blox接收机解算得到的姿态角偏差序列波动趋势基本相同,其中航向角Heading的波动范围均在0.3°左右,俯仰角Pitch的波动范围大于航向角,达到0.5°左右。由表 1的统计结果可以得出相似的结论,且可以看出GPS+BDS双系统略优于单系统,达到水平2 mm、高程6 mm以及航向角0.15°、俯仰角0.32°的精度水平。表中的正确固定率是指模糊度固定正确的历元个数与总历元个数的比值(模糊度是固定解且在静态观测环境下姿态角与参考值偏差小于2°/m,动态环境下小于3°/m,则认为模糊度正确固定)。可以发现,除u-blox的单BDS外,NovAtel ProPak6和u-blox都可以接近100%固定,具有较高的可靠性。以上结果表明,低成本u-blox和高精度测量型接收机的测姿精度差异不大,且能够满足航向和俯仰分别为0.2°/m和0.4°/m的测姿精度。
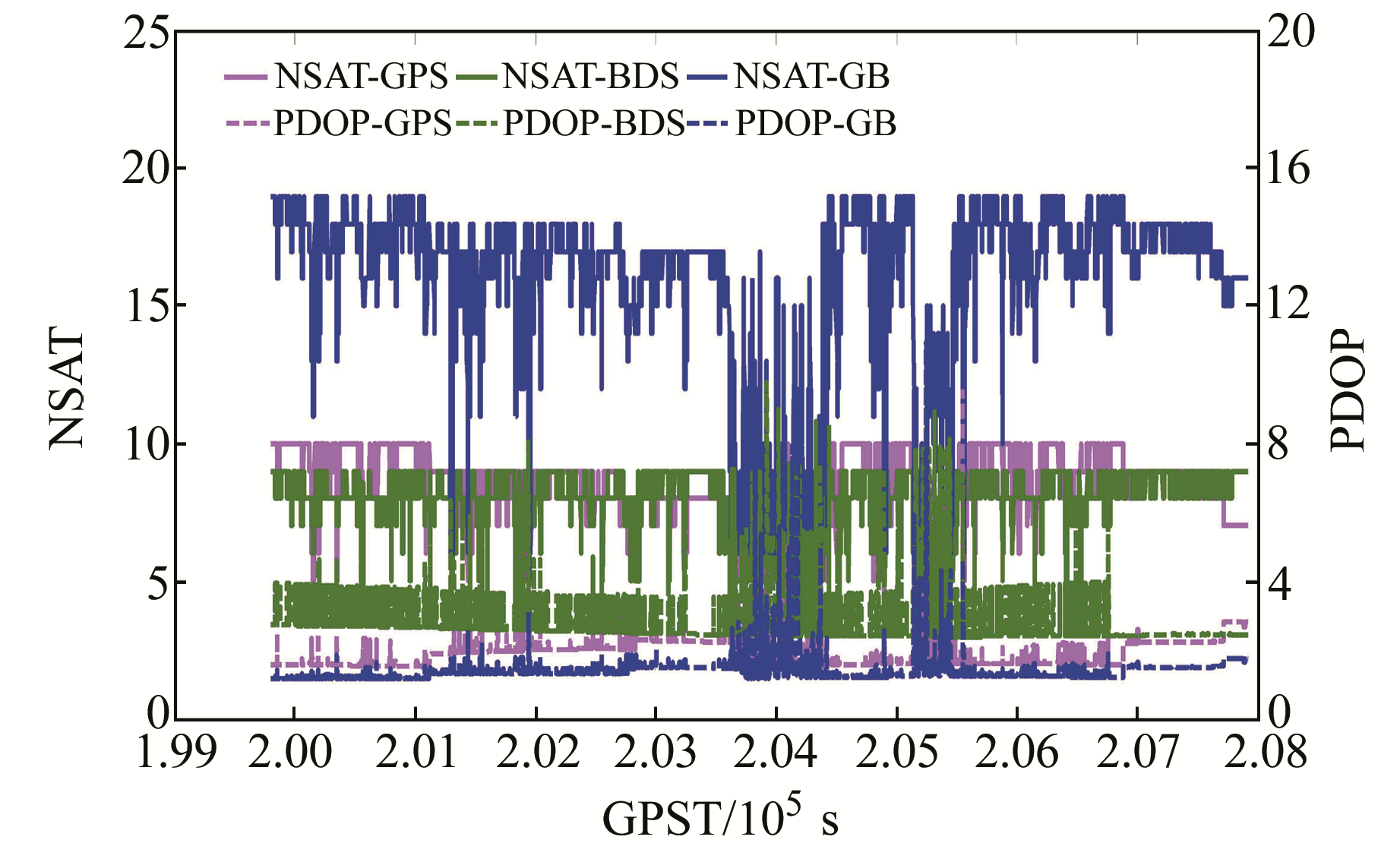
3.2 动态数据测试本组动态数据和第二节的数据质量分析采用同一组数据,图 8给出相应的共视卫星数和DOP值序列图,在GPST 204 000 s前后以及205 000 s后,由于建筑物遮挡,共视卫星数显著减少且PDOP值增大。分别对NovAtel ProPak6和低成本u-blox接收机的数据进行姿态解算,绘制出历元的姿态角偏差序列,如图 9、图 10所示。统计基线向量和姿态角的解算精度,如表 2所示。此外,受遮挡影响GrafMov软件解算结果的模糊度固定率仅87.88%,同时考虑到GrafMov解算得到的参考值也存在误差,根据误差传播定律,表 2中的精度统计结果均已除以
|
图 8 共视卫星数及DOP值 Fig. 8 Number of satellites in common and DOP |

|
图 9 NovAtel ProPak6接收机姿态角解算结果偏差序列图 Fig. 9 Attitude angle bias resolved by NovAtel ProPak6 data |
|
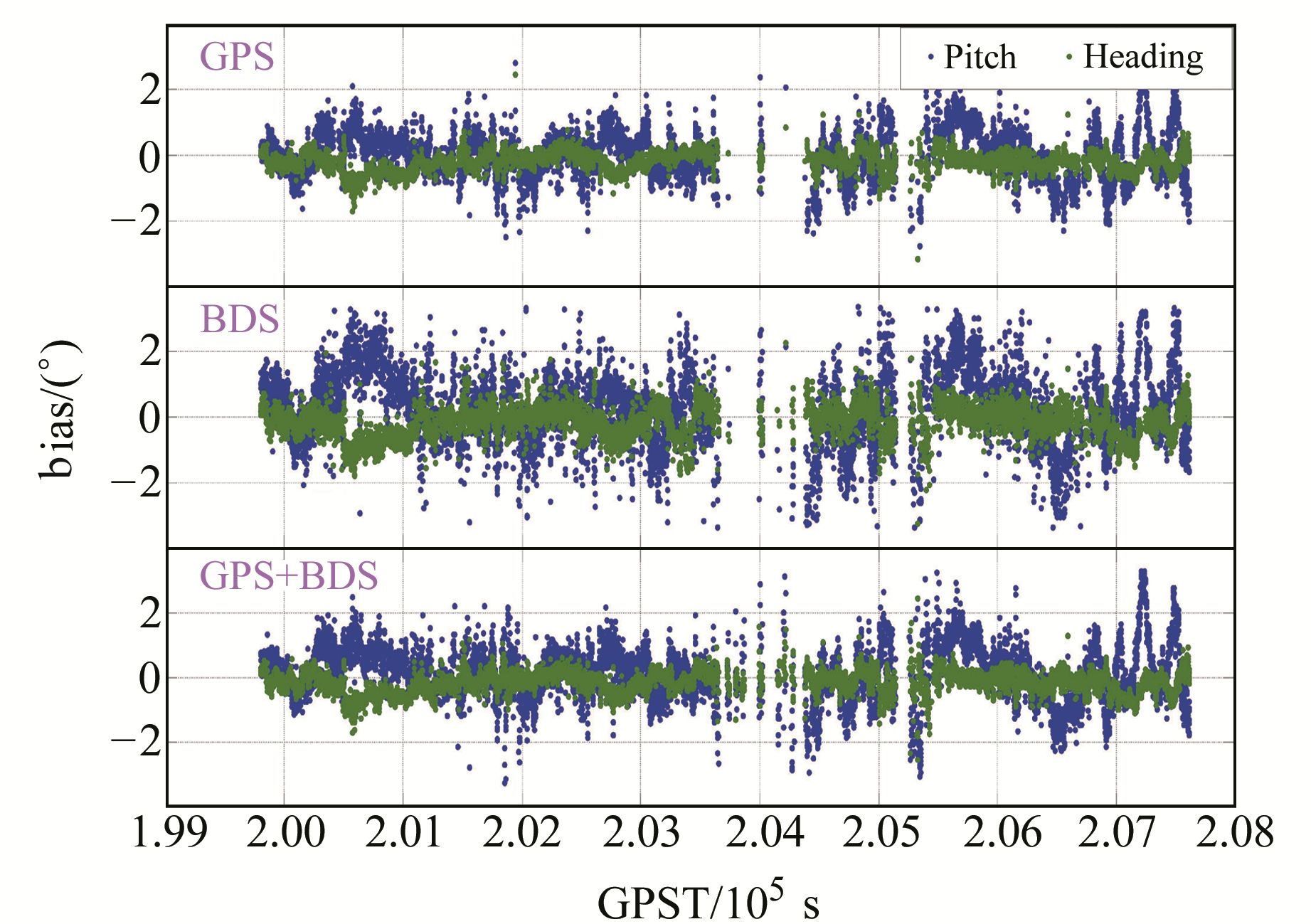
图 10 u-blox接收机姿态角解算结果偏差序列图 Fig. 10 Attitude angle bias resolved by u-blox data |
|
|
表 2 动态实验NovAtel ProPak6和u-blox解算精度 Tab. 2 Resolving accuracy of NovAtel ProPak6 and u-blox in kinematic experiment |
由图 9、图 10可以看出,NovAtel ProPak6和u-blox解算得到的姿态角偏差序列波动趋势基本相同,其中航向角Heading的波动范围在1°左右,俯仰角Pitch的波动范围在2°左右;单BDS的偏差序列波动范围略大于单GPS和GPS+BDS。结合图 8可以发现,BDS的卫星数和PDOP值变化较大,其表现要差于GPS。此外,在GPST204 000 s附近和GPST 205 000 s后,NovAtel ProPak6和u-blox均有部分历元的解算结果出现缺失,且u-blox缺失情况更为严重,其主要原因是受建筑物遮挡导致观测数据质量较差,模糊度错误固定或未固定,解算结果偏差较大并超出了统计范围。
由表 2可知,NovAtel ProPak6接收机的模糊度正确固定率高于u-blox,这和图 9、图 10的结果是一致的,说明在动态条件下,u-blox接收机的可靠性和可用性要略差于测量型接收机。从姿态角的统计结果可以看出,无论是单GPS、单BDS还是GPS+BDS双系统,NovAtel ProPak6和u-blox的解算精度都很接近,其中单GPS解算精度最高,单BDS精度最差,GPS+BDS受BDS影响而略差于单GPS。对于GPS+BDS双系统,两种接收机均可以达到水平5~7 mm、高程11 mm以及航向角0.27°、俯仰角0.62°的精度水平。相比于静态数据,动态数据定位和定向精度都相对较差,这是由于动态实验的观测环境更加复杂,受卫星初升、遮挡等影响更加频繁。以上结果表明,低成本u-blox接收机和高精度测量型接收机的测姿精度差异不大,能够满足航向和俯仰分别为0.3°/m和0.6°/m的测姿精度,但是在可靠性和可用性上要略差于测量型接收机。
4 结语本文首先从卫星信号信噪比、相位观测值精度和伪距观测值精度3个方面对u-blox接收机的数据质量进行评估,然后分别采用GPS/BDS静态和动态实测数据对u-blox接收机的定向精度进行评估,并与测量型接收机NovAtel ProPak6的结果进行对比分析。结果表明,u-blox接收机的数据质量良好,其GPS、BDS的伪距精度分别为0.91 m、0.56 m,相位精度分别为1.35 cm、1.20 cm,可以满足高精度定位定向的需求。对于1 m长基线,u-blox接收机在静态观测环境下可以达到航向角0.2°和俯仰角0.4°的定向精度;在动态观测环境下可以达到航向角0.3°和俯仰角0.6°的定向精度,该精度水平比测量型接收机单频数据的定向精度稍差。
| [1] |
李征航, 刘万科, 楼益栋. 基于双频GPS数据的单历元定向算法研究[J]. 武汉大学学报:信息科学版, 2007, 32(9): 753-756 (Li Zhenghang, Liu Wanke, Lou Yidong. Heading Determination Algorithm with Single Epoch Dual-Frequency GPS Data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(9): 753-756)
(  0) 0) |
| [2] |
唐卫明, 孙红星, 刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J]. 武汉大学学报:信息科学版, 2005, 30(5): 444-446 (Tang Weiming, Sun Hong-xing, Liu Jingnan. Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 444-446)
(  0) 0) |
| [3] |
Takasu T, Yasuda A.Evaluation of RTK-GPS Performance with Low-Cost Single-Frequency GPS Receivers[C].International Symposium on GPS/GNSS, Tokyo, 2008
(  0) 0) |
| [4] |
Odolinski R, Teunissen P J G. Single-Frequency, Dual-GNSS Versus Dual-Frequency, Single-GNSS:A Low-Cost and High-Grade Receivers GPS-BDS RTK Analysis[J]. Journal of Geodesy, 2016, 90(11): 1-24
(  0) 0) |
| [5] |
Mongrédien C, Doyen J P, Strom M, et al.Centimeter-Level Positioning for UAVs and Other Mass-Market Applications[C].ION GNSS, Oregon, 2016
(  0) 0) |
| [6] |
Zuo X, Chen Y J, Li C G, et al.Single Frequency GPS/BDS Precise Positioning Algorithm for Low-Cost Receivers[C].ION GNSS, Oregon, 2016
(  0) 0) |
| [7] |
Liu W K, Li J L, Zeng Q, et al.An Improved Robust Kalman Filtering Strategy for GNSS Kinematic Positioning Considering Small Cycle Slips[J/OL].Advances in Space Research, https://doi.org/10.1016/j.asr.2017.11.041
(  0) 0) |
| [8] |
Teunissen P J G, Giorgi G, Buist P J. Testing of a New Single-Frequency GNSS Carrier Phase Attitude Determination Method:Land, Ship and Aircraft Experiments[J]. GPS Solutions, 2011, 15(1): 15-28
(  0) 0) |
| [9] |
卢立果.GNSS整数最小二乘模糊度解算理论与方法研究[D].武汉: 武汉大学, 2017 (Lu Liguo.Study on Theory and Method of GNSS Integer Least Squares Ambiguity Resolution[D].Wuhan: Wuhan University, 2017)
(  0) 0) |
| [10] |
NovAtel.Enclosures ProPak6[EB/OL].https://www.novatel.com/assets/Documents/Papers/ProPak6-PS-D18297.pdf, 2018
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2019, Vol. 39
2019, Vol. 39

