多路径效应带来的误差是指卫星发射信号的原始路径与环境反射产生的次要路径混合后被接收机接收,从而产生测距延迟。多路径效应在高层建筑旁、山谷、盆地、金属矿区及水面等环境中尤其显著,测量时选择开阔的地区可以减弱多路径效应。然而进行海洋、湖泊等水面测量时,来自水平线以下的信号却无法避免。测量型GNSS接收机通常装有扼流圈天线,可以很好地减弱来自水平线以下的反射信号,但前提是天线姿态需要时刻垂直向上,这在地基静态测量时可以很好保持[1-3]。但动态测量时,诸如车辆、船舶等天线载体由于受到地形、海上风浪等自然环境影响,天线无法保持垂直向上的姿态。当天线发生倾斜时,扼流圈天线作用被削弱,使水平线以下反射信号进入接收机中,从而增大多路径效应造成的延迟。本文首先建立倾斜天线与卫星间的相对位置关系,设计具体实验采集观测数据,计算所有可见星的多路径效应,然后分析不同方位的卫星在天线不同倾角的姿态下多路径效应的变化规律。
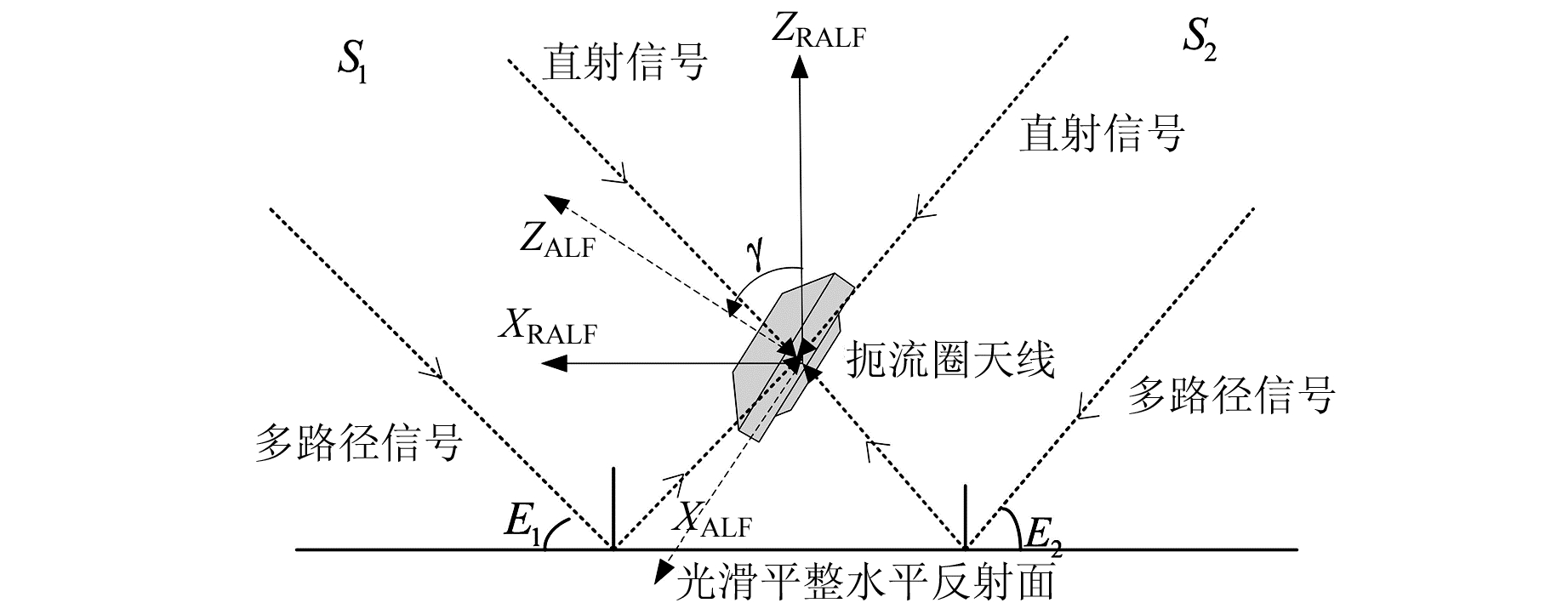
1 相关坐标系的建立及坐标归算为研究天线姿态对卫星信号多路径效应的影响规律,首先要确立卫星与倾斜天线间的空间位置关系,需要建立与之相关的坐标系统(见图 1),图 1(b)是图 1(a)虚线框内的详细示意图;然后通过对各坐标系统进行相互转换,实现在统一框架下的坐标归算。

|
图 1 相关坐标系空间示意图 Fig. 1 Relevant coordinate system space diagram |
在接收机天线坐标系(antenna level frame, ALF)中,坐标系原点为天线几何中心,Z轴在天线垂直对称轴上,方向指向天线上半球为正,X轴与Z轴垂直指向天线倾斜方向,Y轴与X轴、Z轴构成右手坐标系。接收机天线坐标系与天线姿态是绑定的,坐标系随天线姿态的变化而变化。在图 1(b)中,接收机天线坐标系以下标ALF标出。
1.1.2 接收机天线水平坐标系在接收机天线水平坐标系(receiver antenna level frame, RALF)中,坐标系原点为天线几何中心,Z轴垂直于水平面指向天顶,X轴为ALF坐标系XALF轴在水平面上的投影,Y轴与X轴、Z轴构成右手坐标系。与ALF坐标系不同,RALF坐标系不随天线姿态变化而变化。当天线垂直向上时,两坐标系重合。在图 1(b)中,接收机天线水平坐标系以下标RALF标出。
1.1.3 站心坐标系站心坐标系(local level frame, LLF)的原点为天线几何中心,Z轴垂直于水平面指向天顶,X轴指向经过接收机天线几何中心的子午线,以北为正,Y轴与X轴、Z轴构成左手坐标系,以东向为正。当天线倾斜方向为真北时,RALF与LLF坐标系重合。在图 1(b)中,站心坐标系以下标LLF标出。
1.1.4 地心地固坐标系地心地固坐标系(earth-centered & earth-fixed, ECEF)是卫星的坐标系,原点位于地球质心,Z轴指向国际地球自转服务组织(IERS)定义的参考极(IRP)方向,X轴指向IERS定义的参考子午面(IRM)和赤道的交点,Y轴与X轴、Z轴构成右手坐标系。在图 1(a)中,地心地固坐标系以下标ECEF标出。
1.1.5 大地坐标系大地坐标系是以参考椭球面为基准面建立起来的坐标系统。地面某一接收机P的点位坐标可用纬度B、经度L和大地高程H表示,即P(BP, LP, HP)。纬度BP是P点在地球表面的法线与赤道面的夹角,由赤道面起算,范围0°~90°,向北为正,向南为负;经度LP是过P点的子午面与本初子午面的夹角,由本初子午面起算,范围0°~180°,向东为正,向西为负;大地高程HP是P点到地球表面的距离。
1.2 坐标归算为确立卫星与倾斜天线间的空间位置关系,需要将各坐标系统在统一框架下归算。以接收机天线水平坐标系为基准框架,首先将卫星地心坐标系转换到站心坐标系,然后通过空间旋转矩阵,将站心坐标系转换到接收机天线水平坐标系。
1.2.1 地心坐标系转换为站心坐标系将卫星地心地固坐标系转换为站心坐标系,则卫星S在站心坐标系中的坐标为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{X_{\rm{LLF}}}}\\ {{Y_{\rm{LLF}}}}\\ {{Z_{\rm{LLF}}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} { - \sin {B_P}\cos {L_P}}&{ - \sin {B_P}\sin {L_P}}&{\cos {B_P}}\\ { - \sin {L_P}}&{\cos {L_P}}&0\\ {\cos {B_P}\cos {L_P}}&{\cos {B_P}\sin {L_P}}&{\sin {B_P}} \end{array}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {{X_S} - {X_P}}\\ {{Y_S} - {Y_P}}\\ {{Z_S} - {Z_P}} \end{array}} \right]_{\rm{ECEF}}} \end{array} $ | (1) |
式中,XS、YS、ZS为卫星S在地心空间直角坐标系下的坐标;XP、YP、ZP为接收机P在地心空间直角坐标系下的坐标;LP、BP为接收机P在大地坐标系下的经纬度。
1.2.2 站心坐标系转换为天线水平坐标系对于任意两个原点相同的坐标系统间的变换仅通过旋转即可实现。站心坐标系是左手坐标系,转换为接收机天线水平坐标系首先需改变YLLF轴方向,使其变为右手坐标系。由于ZRALF和ZLLF重合,因此仅需要进行一次旋转,旋转角θ定义为倾斜天线在水平面上的投影与真北方向的夹角,从Z轴正方向看向原点顺时针为正,则两坐标系有如下转换关系:
| $ \left[ {\begin{array}{*{20}{c}} {{X_{{\rm{RALF}}}}}\\ {{Y_{{\rm{RALF}}}}}\\ {{Z_{{\rm{RALF}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }&0\\ { - \sin \theta }&{ - \cos \theta }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{\rm{LLF}}}}\\ {{Y_{\rm{LLF}}}}\\ {{Z_{\rm{LLF}}}} \end{array}} \right] $ | (2) |
由此,地心坐标系转换到接收机天线水平坐标系的空间变换矩阵R为:
| $ {\mathit{\boldsymbol{R}}} =\\\; \left[ {\begin{array}{*{20}{c}} { - \sin {B_p}\cos {L_P}\cos \theta + \sin {L_P}\sin \theta }&{ - \sin {B_p}\sin {L_P}\cos \theta }&{\cos {B_P}\cos \theta }\\ {\sin {B_p}\cos {L_P}\sin \theta + \sin {L_P}\cos \theta }&{\sin {B_p}\sin {L_P}\sin \theta - \cos {L_P}\cos \theta }&{ - \cos {B_P}\sin \theta }\\ {\cos {B_p}\cos {L_P}}&{\cos {B_p}\sin {L_P}}&{\sin {B_P}} \end{array}} \right]~~~~~~~~~~~~~~~~(3) $ |
当天线姿态发生改变时,受扼流圈天线影响,位于不同方位、不同高度的卫星信号将产生不同的变化。卫星与接收机的相对位置如图 2所示,S1、S2代表卫星,由于卫星相对于天线位置距水平反射面很远,因此可以认为同一颗卫星的信号到达天线和反射面是平行的,即高度角一致,γ是天线倾角。由于天线姿态发生改变,为方便构建卫星与倾斜天线的相对位置关系,采取相对方位及相对高度角表示。相对方位用坐标XRALF判断,以天线水平坐标系(YOZ)RALF平面为界,当卫星S1位于天线倾斜面对方向时XRALF>0;当卫星S2位于天线倾斜背对方向时XRALF<0。相对高度角定义为卫星高度角在(YOZ)RALF平面的投影:
|
图 2 卫星与接收机的相对位置示意图 Fig. 2 Satellite and receiver relative position diagram |
| $ E = \arctan \frac{{{Z_{\rm{RALF}}}}}{{{X_{\rm{RALF}}}}} $ | (4) |
理论上,对于天线面对的卫星S1,当卫星相对高度角E-γ>0,S1的多路径信号会被扼流圈削弱;当E-γ<0,由于天线倾斜,来自水平面的多路径信号将被天线接收。对于天线背对的卫星S2, XRALF<0,此时来自水平面的反射信号会被扼流圈削弱,当卫星高度角E-γ>0,卫星直射信号能够被正常接收;当E-γ<0时,卫星直射信号会被扼流圈天线削弱。详细比较见表 1。
|
|
表 1 卫星与倾斜天线相对位置对信号的影响 Tab. 1 The relative position of the satellite and the tilted antenna affects the signal |
多路径效应的计算包括伪距多路径效应和相位多路径效应,一般以MP1和MP2分别表示GNSS的L1和L2载波上的多路径效应对伪距和相位影响的综合指标,其结果以均方根(RMS)表示,单位为m,通常以MP1和MP2不超过0.5作为信号质量评价时的重要衡量指标[4-5],计算公式为:
| $ {\rm{M}}{{\rm{P}}_1} = {\rho _1} - [1 + \frac{2}{{\alpha - 1}}]{\varphi _1} + [\frac{2}{{\alpha - 1}}]{\varphi _2} $ | (5) |
| $ {\rm{M}}{{\rm{P}}_2} = {\rho _2} - [1 + \frac{{2\alpha }}{{\alpha - 1}}]{\varphi _1} + [\frac{{2\alpha }}{{\alpha - 1}}]{\varphi _2} $ | (6) |
式中,ρ1、ρ2为L1和L2载波的伪距观测量;φ1、φ2为L1和L2载波的相位观测量;α=(f1/f2)2,f1、f2为L1和L2载波频率。
3 实验验证 3.1 静态实验 3.1.1 实验策略影响多路径效应的环境因素主要有两点[6-8]:反射系数及反射面距天线的距离。越光滑平整的反射面,反射系数越高;通常50 m以外的多路径信号强度衰减100 dB,可以不必考虑。因此实验设计时选择舰院1号实验楼楼顶平台,实验楼位于山顶,周围100 m内没有高于楼顶平台的建筑,平台表面平整。实验选用两台GNSS接收机,一台接收机天线始终保持垂直姿态,另一台按照时间顺序依次变换10次倾角。数据采集后分别计算两台接收机观测到的每颗卫星在每个采样时刻的多路径效应MP1、MP2,以垂直天线观测数据解算结果作为真值求得偏差ΔMP1、ΔMP2,并统计每个倾角下观测历元的平均偏差ΔMP1、ΔMP2。由于实验要对不同天线姿态下解算结果作横向比较,实验时间过长会引入卫星高度角变化带来的误差,从而导致误差源难以剥离;而且当天线姿态发生变化时,所对应的多路径延迟是瞬时发生改变的,短时间实验也能分析出天线倾斜对多路径的效应影响规律,因此观测时间控制在1 h以内,观测时间段为2017-11-21 08:56:30~10:39:30,观测历元共3 000个,其中不包括调整天线姿态的时间,具体实验策略如表 2所示。
|
|
表 2 具体实验策略 Tab. 2 Specific experimental strategy |
整个观测历元中共23颗观测卫星,其中包含8颗GPS卫星G2、G5、G6、G9、G12、G19、G25、G29,6颗GLONASS卫星R2、R3、R4、R17、R18、R19,9颗BDS卫星C1、C3、C4、C5、C6、C8、C9、C13、C14。按照实验策略,求得每颗卫星在每个倾角的平均偏差ΔMP1、ΔMP2。根据观测卫星数将实验结果分成23组,每组包含10个倾角的多路径效应的平均偏差。按照§2.1中卫星与倾斜天线的相对位置关系,将这23组卫星分成3类:天线倾斜面对的卫星(XRALF>0)、天线倾斜背对的卫星(XRALF<0)及观测历元中轨迹经过天顶的卫星(XRALF≈0)。处于不同方位的卫星随天线不同倾角的ΔMP1、ΔMP2的角度序列见图 3,分别对与倾斜天线不同相对位置关系卫星的多路径效应变化规律作具体分析。

|
图 3 不同方位卫星随天线不同倾角的ΔMP1、ΔMP1的角度序列 Fig. 3 Angle sequence of ΔMP1、ΔMP2 with different inclination angles of satellites with different orientations |
1) 天线倾斜面对的卫星信号多路径效应分析。整个观测历元中,始终处于天线倾斜面向方位(XRALF>0)的卫星包括G6、G9、G19、R17、C1、C3、C4、C8、C14,共形成9组数据,其随天线不同倾角的ΔMP1、ΔMP2的角度序列见图 3(a)、(b),其中G19和C14在部分观测历元高度角低于截止高度角15°,因而在这段观测历元没有数据。如图 3所示,当卫星与倾斜天线的相对位置关系满足E-γ>0时,ΔMP1、ΔMP2基本保持不变,维持在0.1以下;当E-γ<0时,ΔMP1、ΔMP2随天线倾斜角度的增大而增大,且增大到一定值后趋于稳定,此时这9颗卫星的MP1和MP2如表 3所示,多颗卫星信号的MP1和MP2超过0.5,多路径效应明显。当E-γ<0时扼流圈无法阻挡反射信号,反射信号直接被天线接收,多路径效应增大,实验结果符合理论分析。
|
|
表 3 XRALF>0、E-γ<0时9颗卫星的MP1和MP2 Tab. 3 MP1 & MP2 of 9 satellites multipath effects in XRALF>0 and E-γ < 0 |
2) 天线倾斜背对的卫星信号多路径效应分析。整个观测历元中,始终处于天线倾斜背对方位(XRALF<0)的卫星包括G5、G12、G25、G29、R19、C5、C13,共形成7组数据,其随天线不同倾角的ΔMP1、ΔMP2的角度序列见图 3(c)、(d),其中G12、G25、G29和R19在部分观测历元高度角低于截止高度角15°,因而在这段观测历元没有数据。整体上各卫星的多路径效应偏差随着天线倾斜角度的增大而增大。当卫星与倾斜天线的相对位置关系满足E-γ>0时,ΔMP1、Δ MP 2随着天线的倾斜而增大缓慢,各卫星的MP增加幅度为3.7%、0.6%、1%、0%、2.5%、6.7%、2.4%,说明扼流圈天线并不能完全阻止接收多路径信号;当E-γ<0时,ΔMP1、ΔMP2随着天线的倾斜而明显增大,各卫星的MP增加幅度为9.8%、7.5%、13%、9.4%、11.6%、18.7%、4%,相比E-γ>0时多路径效应综合指标增幅明显增大,其中C5卫星在天线倾斜40°后,直射信号被扼流圈完全阻断,造成信号失锁。此时这7颗卫星的MP1和MP2如表 4所示,大部分卫星的MP1和MP2大于0.5,多路径效应非常明显。当E-γ<0时,扼流圈同时削弱卫星的直射信号和反射信号,实验结果符合理论分析。
|
|
表 4 XRALF<0、E-γ<0时7颗卫星的MP1和MP2 Tab. 4 MP1 & MP2 of 7 satellites multipath effects in XRALF < 0 and E-γ < 0 |
3) 轨迹穿过(YOZ)RALF面的卫星信号多路径效应分析。轨迹穿过(YOZ)RALF面的卫星包括G2、R2、R3、R4、R18、C6、C9,共形成7组数据,其随天线不同倾角的ΔMP1、ΔMP2的角度序列见图 3(e)、(f)。虚线窗口为卫星在天线天顶方位即XRALF≈0;先后经历倾斜天线背向、天顶、面向方位的卫星有G2、R2和R18;先后经历倾斜天线面向、天顶、背向方位的卫星有R3、R4、C6和C9。如图 4所示,卫星位于天顶方位时, 由于其相对高度角接近90°,E始终大于γ,因此ΔMP变化很小;卫星位于倾斜天线背向和面向方位时,ΔMP变化规律符合前文分析结果,进而验证了理论分析的正确性。
3.2 动态实验 3.2.1 实验策略动态实验旨在模拟动态测量时天线姿态不断改变的过程,本实验模拟典型的海上船载天线受风浪作用下不断发生横摇的状态,定性分析动态测量时天线姿态不断改变对多路径效应、有效观测值及单点定位精度的影响。在舰院1号实验楼顶采用两台iRTK2接收机,一台天线姿态垂直固定作为基准站A,另一台在北偏东125°方向上随机摇摆,作为动态监测站B。为避免引入卫星高度角变化带来的观测误差,实验时间为2017-11-27 13:05:30~14:05:30,截止高度角为15°,采样间隔1 s。
3.2.2 实验结果分析整个观测历元共23颗观测卫星,包含7颗GPS卫星G2、G5、G6、G9、G13、G20、G29,6颗GLONASS卫星R3、R4、R5、R18、R19、R20,10颗BDS卫星C1~C6、C8、C9、C13、C14。
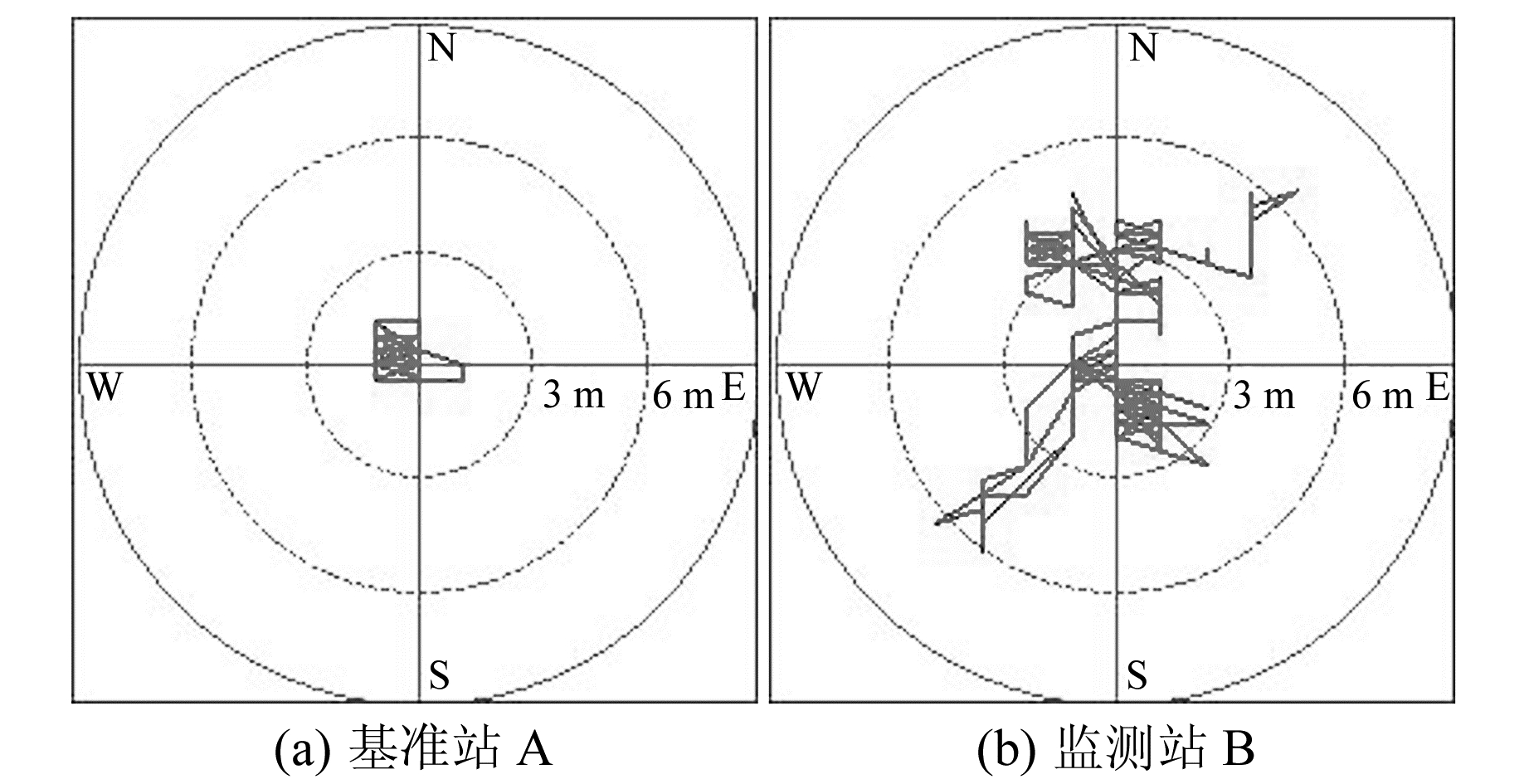
A站和B站各观测卫星多路径效应综合指标及有效观测值百分比如图 4所示。实验中A站各观测卫星MP1和MP2的RMSE值较低,受个别卫星信号质量影响,指标值在0.14~0.36;动态监测站各观测卫星MP1和MP2较基准站有明显增加,指标值在0.26~0.9,其中MP1和MP2超过0.5的卫星占1/3。各观测卫星有效观测值百分比情况:基准站在94.3%以上,动态测量站在47.2%以上,其中有效观测值在90%以上的仅占60%。两站单点定位结果如图 5所示,B站(图 5(b))明显比站A(图 5(a))定位误差大,且MP1和MP2的RMS同比增大0.15 m和0.16 m。实验数据说明,动态测量时,当天线姿态不断发生倾斜时会明显增加多路径效应,降低有效观测值数量,对定位精度产生严重影响。

|
图 4 各卫星的多路径效应综合指标(MP)及有效观测值百分比 Fig. 4 The multipath effects composite indicators and the percentage of valid observations for each satellite |
|
图 5 单点定位结果比较 Fig. 5 Single-point positioning results comparison |
通过构建GNSS卫星与倾斜天线的空间位置关系模型,基于理论分析与实验验证,天线倾斜姿态对卫星信号的多路径效应影响规律如下:
1) 当天线不断处于动态倾斜姿态时,多路径效应明显增加,有效观测值数量降低,定位精度变差。通过实验证明,天线倾斜姿态下多路径延迟的大小与天线倾斜方向、角度有关。
2) 卫星处于天线倾斜面对方向(XRALF>0),当卫星相对高度角大于天线倾角时,此类卫星信号的多路径效应不受天线姿态变化的影响;当卫星相对高度角小于天线倾角时,多路径延迟大小随天线倾角的增大而增大,且增大到一定值后趋于稳定。
3) 卫星处于天线倾斜背对方向(XRALF<0),各卫星信号的多路径延迟随天线倾斜角度的增大而增大。当卫星相对高度角大于天线倾角时,此类卫星信号的多路径延迟随着天线的倾斜而增大缓慢;当卫星相对高度角小于天线倾角时,多路径延迟随天线倾斜角度的增大而显著增大,甚至部分卫星信号完全失锁。
4) 卫星位于倾斜天线天顶方位时(XRALF≈0), 由于其相对高度角接近90°,多路径延迟不受天线倾斜姿态的影响。
| [1] |
范晓燕, 周乾. GPS测量中多路径效应研究综述[J]. 工程地球物理学报, 2010, 7(3): 382-386 (Fan Xiaoyan, Zhou Qian. A Review of Multipath Effects in GPS Surveys[J]. Journal of Engineering Geophysics, 2010, 7(3): 382-386)
(  0) 0) |
| [2] |
宋乐, 曾志. GPS载波相位的多路径效应空间相关性分析[J]. 科技创新导报, 2015, 12(11): 41-43 (Song Le, Zeng Zhi. Spatial Correlation Analysis of Multipath Effect of GPS Carrier Phase[J]. Science and Technology Innovation Review, 2015, 12(11): 41-43 DOI:10.3969/j.issn.1674-098X.2015.11.023)
(  0) 0) |
| [3] |
Georgiadou Y, Kleusberg A. On Carrier Signal Multipath Effects in Relative GPS Positioning[J]. Manuscripta Geodaetica, 1998(13): 172-179
(  0) 0) |
| [4] |
田宗彪, 章磊, 张训虎, 等. GNSS点位质量评定中多路径效应分析研究[J]. 工程勘察, 2017, 45(2): 45-48 (Tian Zongbiao, Zhang Lei, Zhang Xunhu, et al. Analysis of Multipath Effect in GNSS Point Quality Evaluation[J]. Geotechnical Investigation & Surveying, 2017, 45(2): 45-48)
(  0) 0) |
| [5] |
唐龙江, 徐爱功, 徐宗秋, 等. 复杂环境下多模GNSS接收机性能评估[J]. 导航定位学报, 2017, 5(4): 105-109 (Tang Longjiang, Xu Aigong, Xu Zongqiu, et al. Performance Evaluation of Multimode GNSS Receiver in Complex Environment[J]. Journal of Nautical Navigation, 2017, 5(4): 105-109)
(  0) 0) |
| [6] |
刘永义, 党亚民, 薛树强. 基于海面环境多路径效应建模初探[J]. 测绘科学, 2013, 38(1): 122-124 (Liu Yongyi, Dang Yamin, Xue Shuqiang. Study on Multi-Path Effect Modeling Based on Sea Surface Environment[J]. Science of Surveying and Mapping, 2013, 38(1): 122-124)
(  0) 0) |
| [7] |
Yi T H, Li H N, Gu M. Effect of Different Construction Materials on Propagation of GPS Monitoring Signals[J]. Measurement, 2012, 45(5): 1 126-1 139 DOI:10.1016/j.measurement.2012.01.027
(  0) 0) |
| [8] |
Fan K K, Ding X L. Estimation of GPS Carrier Phase Multipath Signals Based on Site Environment[J]. Journal of Global Positioning Systems, 2006, 5(2): 22-28
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


