2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
利用GNSS多天线实现移动平台的精密定位测姿是近年发展起来的一项导航新技术,在海洋、航空等不利于布设参考站情况下具有广泛的应用前景[1]。目前GNSS精密定位可以实现实时dm级、事后cm级精度水平[2],满足高精度定位需求。但精密定姿由于受移动平台范围的限制,多个天线形成的基线长度比较短,一般只有几米,姿态精度受基线解算精度的影响较大,需要每个历元提供多天线之间mm级精度的基线矢量,因此多条基线模糊度的快速、正确解算仍是这一技术面临的挑战,也是近年来多天线测姿研究的热点[3]。
针对移动平台上GNSS天线之间形成的具有固定几何关系的短基线模糊度单历元解算问题,很多学者提出一些新的附加约束的处理策略。唐卫明等[4]提出附加已知基线长度约束的方法;Teunissen[5]根据多个天线之间的固定长度和角度关系,提出附加多元约束的LAMBDA方法,即MC-LAMBDA法;Wang[6]根据天线间夹角不变的性质,提出附加固定角约束的模糊度解算法。这些改进算法通过增加已知观测信息,改善观测模型法矩阵的病态性,提高模糊度实数解及其方差-协方差阵估计的准确性,缩小模糊度搜索空间,提高了模糊度解算的成功率。这些方法的验证一般采用静态数据或仿真数据,观测质量比较好时,模糊度固定成功率一般在90%以上。动态环境下,卫星信号失锁严重且观测噪声比较大,单个历元可用的观测信息较少,模糊度动态解算及其正确性检验仍是比较棘手的问题。
近年来,笔者对影响模糊度动态解算的问题进行深入分析发现,影响模糊度实数解及其协方差阵准确性的原因在于,法矩阵总存在3个数值很小的奇异值, 即3个位置参数和模糊度参数不可区分,导致法方程严重病态。要解决这一问题,至少需增加3个独立观测,以减弱法矩阵的病态性。这一思路在位置参数准确已知的快速静态定位中得到了较好的应用。通过实验,对于几km的基线,当近似坐标精度在几dm时,通过附加近似坐标(或近似基线分量)约束,利用5~10个历元的相位观测就可以正确固定模糊度[7]。借鉴这一思想,如何在动态情况下获取准确的近似坐标或基线分量信息是关键。
对模糊度固定正确性检验一般采用ratio值。近年来,有学者发现这一检验量在动态定位中不可靠[8],如果ratio值设置过大,会增加弃真概率,否则会增加纳伪概率。其主要原因在于,ratio值是一个统计指标,样本数量要求足够大,而动态定位时观测信息比较少,因此仅用ratio值作为模糊度检验指标显然不合理。
基于以上分析,本文提出多天线基线网单历元同步解算方法,其主要思路如下:
1) 利用天线之间基线长度固定、宽巷组合观测(L5)波长较长的特点,将多天线形成基线网,采用附加已知基线长度约束同步解算多条基线的宽巷模糊度,得到天线之间dm~cm级精度的近似基线分量;
2) 将解算所得近似基线分量作为先验信息,同步解算各基线的基频模糊度,获取mm级精度的基线矢量;
3) 对基线网多组宽巷模糊度进行检验时,联合基线误差、单位权中误差估值、基线网模糊度闭合环及ratio值等综合信息进行检验。
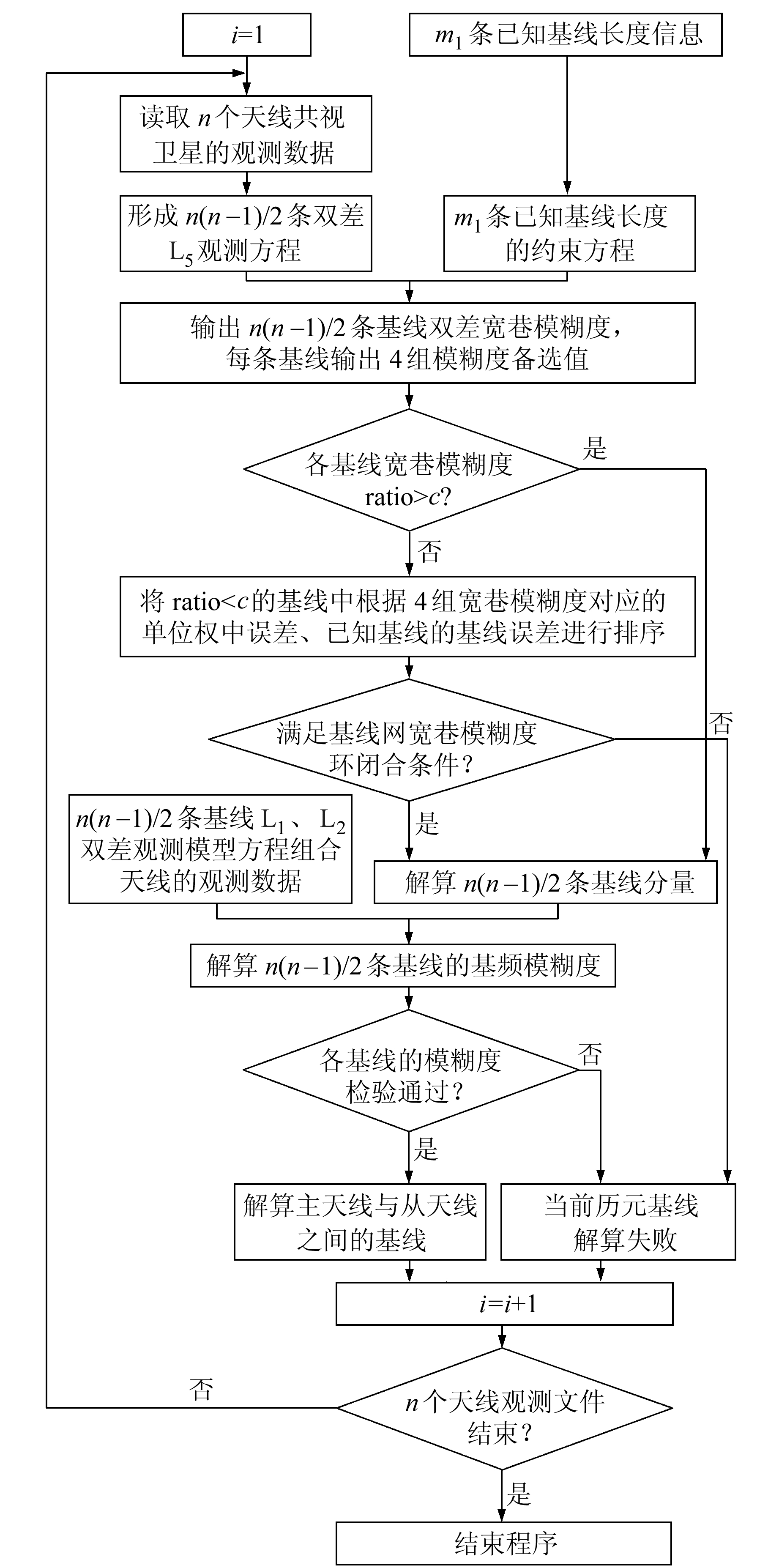
1 GNSS多天线基线网单历元同步解算模型由于GNSS宽巷组合模型、码和相位观测的双差定位模型等在很多文献中都有详细描述,在此不再赘述。本文重点介绍多天线基线网单历元同步解算的思想和处理策略,其整体处理思路如图 1所示。
|
图 1 多天线基线网单历元同步解算实施流程 Fig. 1 The flow chart of the calculating scheme |
图 1中,i为历元号,n表示天线数,m1为已知的基线数。为了保证动态基线解算的可用性,c取2.5[8]。
1.1 基线网伪距和相位宽巷组合定位观测模型n个天线同步观测卫星m颗,其中1号天线为主天线(参考站),不考虑多路径效应,采用伪距和宽巷组合相位观测进行基线解算的模型为[9]:
| $ \begin{array}{*{20}{c}} {\nabla \Delta p_{{r_2}{r_1}}^{{s_1}{s_2}} = \nabla \Delta \rho _{{r_2}{r_1}}^{{s_1}{s_2}} - \nabla \Delta \mathit{\boldsymbol{u}}_{{r_2}{r_1}}^{{s_1}{s_2}}\left({\delta {x_{{r_2}}} - \delta {x_{{r_1}}}} \right) + \varepsilon _{{r_2}{r_1}}^{{s_1}{s_2}}, {\mathit{\boldsymbol{P}}_c}}\\ {\nabla \Delta \varphi {{_{{r_2}{r_1}}^{{s_1}{s_2}}}}_{, j} = \nabla \Delta \rho _{{r_2}{r_1}}^{{s_1}{s_2}} - \nabla \Delta \mathit{\boldsymbol{u}}_{{r_2}{r_1}}^{{s_1}{s_2}}\left({\delta {x_{{r_2}}} - \delta {x_{{r_1}}}} \right) + }\\ {{\lambda _j}\nabla \Delta N{{_{{r_2}{r_1}}^{{s_1}{s_2}}}}_{, j} + \zeta {{_{{r_2}{r_1}}^{{s_1}{s_2}}}}_{, j}, {\mathit{\boldsymbol{P}}_5}} \end{array} $ | (1) |
式中,s1, s2=1, 2, …, m为卫星编号; r1, r2=1, 2, …, n为天线编号; j为观测值频率,这里j=5表示宽巷组合; ▽Δps1s2r2r1、▽Δφs1s2r2r1, j表示双差伪距和双差相位宽巷组合观测值; ▽Δρs1s2r2r1为天线与卫星的双差近似距离; δxr2、δxr1分别为天线r2、r1的位置参数;▽Δus1s2r2r1为系数阵;▽ΔNs1s2r2r1, j为宽巷组合双差模糊度参数;λj≈86 cm为相位宽巷组合观测的波长;εs1s2r2r1、ζs1s2r2r1, j分别为双差伪距观测和双差相位宽巷组合观测值的噪声;Pc、P5为伪距和相位宽巷组合观测值的权阵。n个天线共视m颗卫星,可以形成n(n-1)(m-1)/2个观测方程。
式(1)中由于伪距观测值精度比较低,即Pc比较小,一般为相位观测权阵的1/10 000,而位置信息主要依赖伪距观测,因此,由式(1)直接解算位置和模糊度参数法矩阵对应位置信息的3个特征值非常小,法矩阵病态。
1.2 已知基线长度约束模型若已知天线r1、r2的基线长度为l0r2r1,则其约束模型为:
| $ {L_s} = \mathit{\boldsymbol{G}}(\delta {x_{{r_2}}} - \delta {x_{{r_1}}}), {\mathit{\boldsymbol{P}}_l} $ | (2) |
式中,Ls=|xr2-xr1|-l0r2r1为基线长度约束观测值,|xr2-xr1|为由天线近似坐标计算的近似基线长度,
如果已知m1条基线长度,可以列出m1个基线长度约束观测方程。
1.3 基线网宽巷模糊度同步解算及其检验联立式(1)和式(2)求解各基线的宽巷模糊度实数解及其方差-协方差阵,利用LAMBDA方法可以输出各基线多组宽巷模糊度(本文输出4组)。动态条件下如何检验出正确宽巷模糊度是关键。由于观测信息比较少,如果ratio值设置太大,会导致正确的宽巷模糊度不能通过检验,损失导航信息;反之,不正确的模糊度通过检验,将导致获取错误的导航信息。为了保证宽巷模糊度检验的可靠性,本文ratio值取2.5[8]。
通过对ratio < 2.5的多组宽巷模糊度进行分析发现,在多组宽巷模糊度备选值中可能包含正确的宽巷模糊度,但不是第1组,如果直接依据ratio值,该历元模糊度检验失败,这显然不合理。实际上,多天线基线解算中有一些先验信息、固定条件等可以辅助判断模糊度固定是否正确,如某些基线长度事先已获取、多天线形成闭合环等。结合这些信息,本文提出如下宽巷模糊度检验方法:
1) 如果ratio≥2.5,直接判定该基线第1组宽巷模糊度正确;如果ratio<2.5,若该基线长度已知,将4组宽巷模糊度按解算的基线长度误差由小到大排序,否则,将其按计算的单位权中误差估值由小到大排序。
2) 如果天线r1, r2, …, rn构成闭合环,对各基线对应的第1组宽巷模糊度进行闭合性检验,如果满足如下关系式[10]:
| $ \nabla \Delta N_{{{r}_{1}}}^{{{s}_{1}}}{{_{{{r}_{2}}}^{{{s}_{2}}}}_{, 5}}+\nabla \Delta N_{{{r}_{2}}}^{{{s}_{1}}}{{_{{{r}_{3}}}^{{{s}_{2}}}}_{, 5}}+\cdots +\nabla \Delta N_{{{r}_{n}}}^{{{s}_{1}}}{{_{{{r}_{1}}}^{{{s}_{2}}}}_{, 5}}=0 $ | (3) |
则判断闭合环内各基线模糊度解算正确。
1.4 附加宽巷基线分量约束的基频模糊度解算模型利用上述方法获取该历元所有基线的宽巷基线分量及其方差-协方差阵,将其作为约束信息,解算各基线的基频模糊度。
假设解算出天线r1、r2之间的宽巷基线矢量为Δxr1r2,则其约束方程为:
| $ {v_{{r_1}{r_2}}} = \delta {x_{{r_2}}} - \delta {x_{{r_1}}} - {l_{{r_1}{r_2}}} $ | (4) |
式中,lr1r2=Δxr1r2-x0r2+x0r1为基线约束模型的观测值,x0r1、x0r2对应为天线r1、r2的近似坐标。n(n-1)/2条基线可以建立3n(n-1)/2个基线分量约束方程。
基频模糊度解算的观测方程与式(1)中的相位观测方程类似,其中j=1,2表示L1和L2的观测方程,即
| $ \left\{ \begin{array}{l} \nabla \Delta \varphi {_{{r_2}{r_1}}^{{s_1}{s_2}}}_{, 1} = \nabla \Delta \rho _{{r_2}{r_1}}^{{s_1}{s_2}} - \nabla \Delta \mathit{\boldsymbol{u}}_{{r_2}{r_1}}^{{s_1}{s_2}}\left({\delta {x_{{r_2}}} - \delta {x_{{r_1}}}} \right) + \\ \; \; \; \; \; \; \; {\lambda _1}\nabla \Delta N{_{{r_2}{r_1}}^{{s_1}{s_2}}}_{, 1} + \zeta {_{{r_2}{r_1}}^{{s_1}{s_2}}}_{, 1}, {\mathit{\boldsymbol{P}}_1}\\ \nabla \Delta \varphi {_{{r_2}{r_1}}^{{s_1}{s_2}}}_{, 2} = \nabla \Delta \rho _{{r_2}{r_1}}^{{s_1}{s_2}} - \nabla \Delta \mathit{\boldsymbol{u}}_{{r_2}{r_1}}^{{s_1}{s_2}}\left({\delta {x_{{r_2}}} - \delta {x_{{r_1}}}} \right) + \\ \; \; \; \; \; \; \; {\lambda _2}\nabla \Delta N{_{{r_2}{r_1}}^{{s_1}{s_2}}}_{, 2} + \zeta {_{{r_2}{r_1}}^{{s_1}{s_2}}}_{, 2}, {\mathit{\boldsymbol{P}}_2} \end{array} \right. $ | (5) |
式中,P1、P2分别表示L1和L2观测值的权阵。n个天线共视m颗卫星,可以形成n(n-1)(m-1)/2个观测方程。
联立式(4)和式(5)可知,由于宽巷基线分量约束比伪距定位准确,能有效解决式(5)的秩亏问题,得到比较准确的基频模糊度实数解及其方差-协方差阵,提高了基频模糊度搜索的成功率。一般来说,当宽巷基线解算正确时,LAMBDA方法搜索的第1组基频模糊度为正确的模糊度。
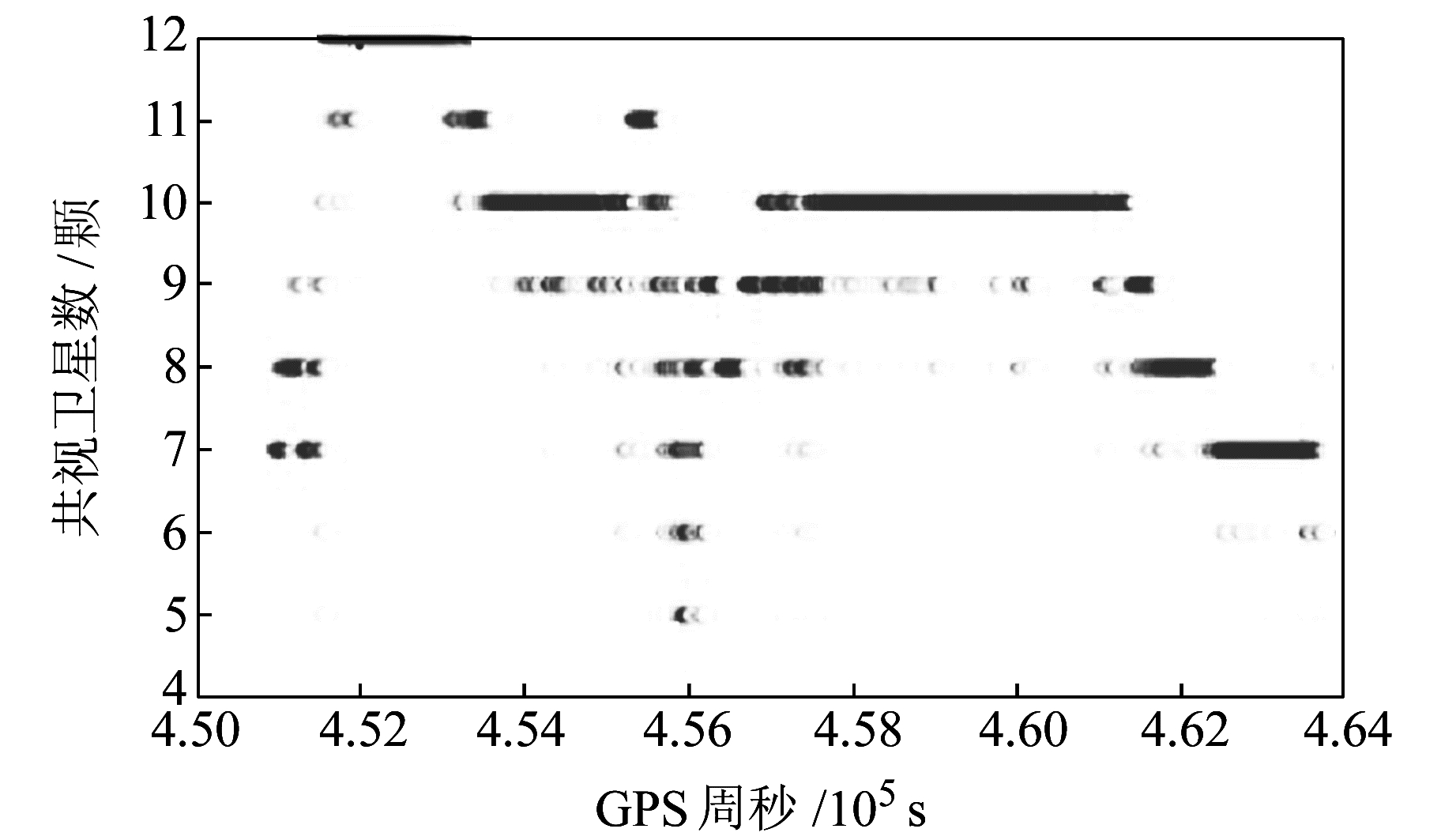
2 实验结果分析 2.1 数据采集车载多天线GNSS数据于2013-12-06在武汉东湖高新技术开发区进行采集,4个天线安装位置如图 2所示, 其中4号天线因故障数据不能用。数据采集前,利用激光测距仪量测基线12和13的长度分别为2.65 m和2.82 m。选取的3个接收机同步观测时段为UTC 05:17:00~08:53:20,数据采样率1 Hz,截止高度角10°。由于2号及3号天线只有GPS数据,本文多天线基线解算采用GPS数据。运动过程中3个天线同步跟踪的卫星数变化如图 3所示。

|
图 2 多天线安装位置图 Fig. 2 Antenna configure |
|
图 3 3个天线同步观测卫星变化 Fig. 3 The common-view satellite number by three antennas |
由图 3可知,在运动过程中,3个天线同步跟踪的卫星数变化比较快,采用多历元或滤波进行模糊度解算,历元间模糊度参数需要不断进行变换处理,比较复杂且效率低,因此本文采用多天线单历元模糊度同步解算。
2.2 多天线基线网模糊度同步解算方案为了验证本文提出的多天线处理方案的优势,设计3种方案进行对比:方案1, 本文提出的多天线基线网单历元模糊度同步解算方案;方案2, 处理流程同方案1,但在宽巷模糊度检验时不进行排序处理;方案3, 常用的附加基线长度约束的多天线模糊度同步解算方案。3种方案基频模糊度解算成功率统计结果见表 1。
|
|
表 1 多天线基线网模糊度同步解算结果 Tab. 1 The results of the resolution |
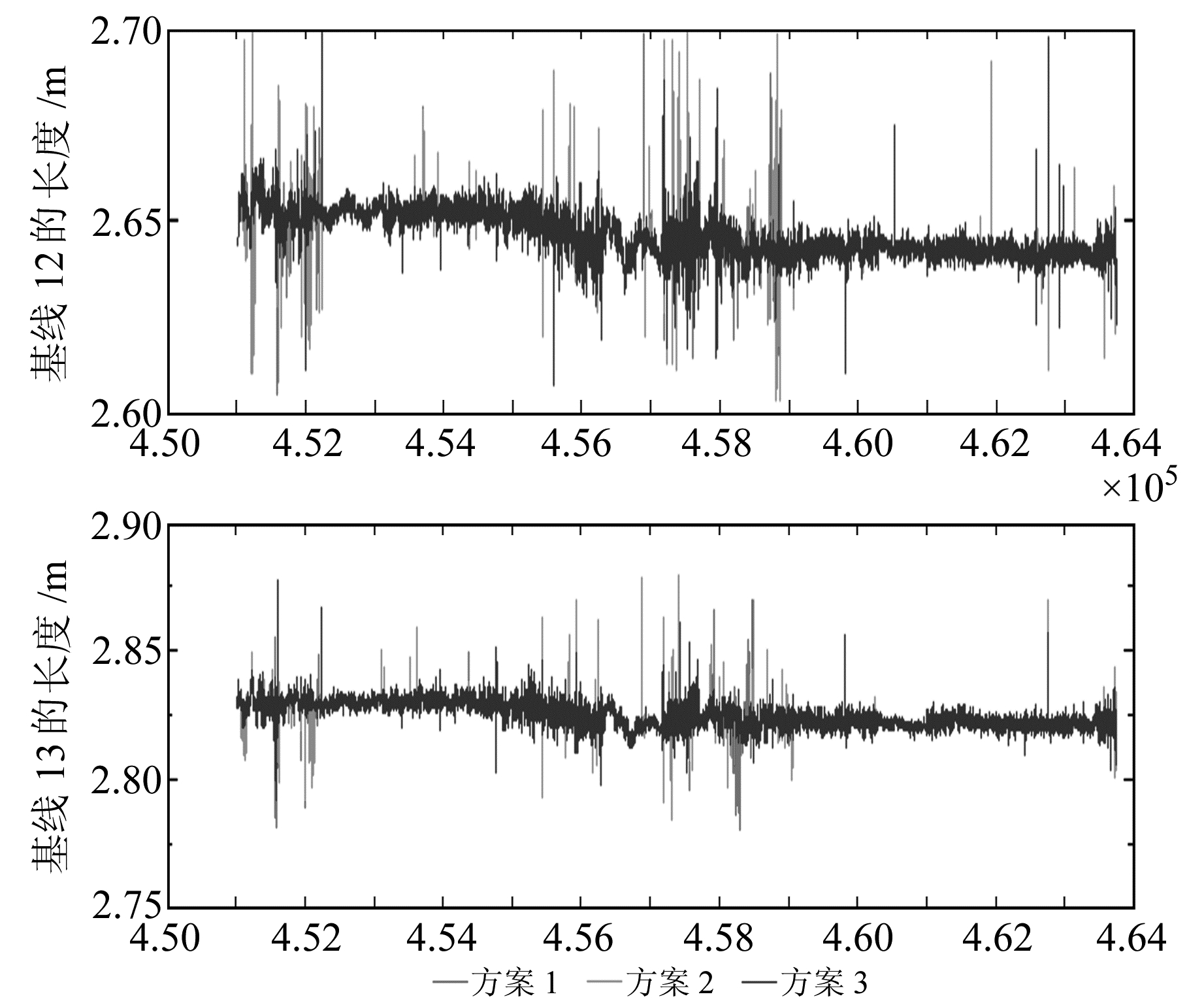
由表 1可知,方案1模糊度解算的成功率比方案2和方案3提高1%~2%,这对移动平台的精密定位定姿非常重要。模糊度解算正确的历元,基线12和基线13的长度计算结果见图 4。
|
图 4 3种方案解算的基线12和基线13的长度 Fig. 4 The length of two baselines obtained using three programs |
由图 4可知,3种方案模糊度固定正确的历元解算的基线12和基线13的长度与激光测距得到的基线长度2.65 m和2.82 m比较接近,其统计结果为:3种方案得到的基线长度均值均为2.646 m和2.825 m,标准偏差均为0.006 m和0.005 m。
为了更好地说明方案1模糊度解算的优势,下面以观测时刻05:17:48数据为例,因为该历元方案1模糊度解算成功,方案2和方案3解算失败。对3种方案的模糊度解算过程进行详细对比分析,结果见表 2~表 4。
|
|
表 2 05:17:48时刻3种方案模糊度解算结果(方案1) Tab. 2 The result of the ambiguity resolution obtained using three programs at 05:17:48(scheme 1) |
|
|
表 3 05:17:48时刻3种方案模糊度解算结果(方案2) Tab. 3 The result of the ambiguity resolution obtained using three programs at 05:17:48(scheme 2) |
|
|
表 4 05:17:48时刻3种方案模糊度解算结果(方案3) Tab. 4 The result of the ambiguity resolution obtained using three programs at 05:17:48(scheme 3) |
表中,ds和
比较方案1和方案2的结果可知,基线13和基线23的L5宽巷模糊度解算的ratio≥2.5,直接判定第1组模糊度正确;基线12的ratio < 2.5,ratio检验不能通过。对基线12输出的4组宽巷模糊度进行分析发现,第2组宽巷模糊度解算的基线误差最小。方案1根据基线误差由小到大对宽巷模糊度进行排序,将第2组的宽巷模糊度排到第1组,而方案2不进行排序处理。对3条基线对应的第1组宽巷模糊度进行闭合环检验,方案1检验正确,方案2检验失败,因此该历元方案2宽巷模糊度解算失败。从基线12和基线13宽巷基线解算的长度也可以看出,宽巷模糊度解算正确时,基线误差在cm级。利用方案1解算各基线的基频模糊度时,可以用3条宽巷基线分量进行准确约束,各基线的第1组基频模糊度均为正确的模糊度。
分析方案3的结果可知,利用附加基线长度约束直接解算基频模糊度,3条基线的ratio值均小于2.5。分析3条基线输出的4组基频模糊度,基线12的4组模糊度均不正确,基线13的正确模糊度为第4组,基线23只有第1组模糊度正确,因此该历元方案3模糊度检验失败。
3 结语1) 本文提出的移动平台多天线基线网同步解算方案的优势是能充分利用多基线之间固定几何关系、多条基线形成的闭合环等条件,提高模糊度解算的成功率。
2) 动态定位中,常用的模糊度检验指标ratio值不可靠,原因在于ratio值是一个统计指标,需要大量样本信息为基础,而单个历元的观测信息量比较少。
3) 本文提出多基线同步解算中模糊度检验的判断准则——综合利用已知基线的基线误差、各基线的单位权中误差、基线网模糊度闭合环及ratio值等对模糊度进行检验,提高了模糊度检验的可靠性。
本文提出的多天线基线网模糊度解算和检验方法还需要进行大量的测试,下一步将基于移动平台上布设不同数量、不同位置分布的多天线情况展开研究,进一步完善该方法。
| [1] |
Teunissen P J G, Giorgi G, Buist P J. Testing of a New Single-Frequency GNSS Carrier Phase Attitude Determination Method: Land, Ship and Aircraft Experiments[J]. GPS Solutions, 2011, 15(1): 15-28 DOI:10.1007/s10291-010-0164-x
(  0) 0) |
| [2] |
Chen W, Qin H. New Method for Single Epoch, Single Frequency Land Vehicle Attitude Determination Using Low-End GPS Receiver[J]. GPS Solutions, 2012, 16(3): 329-338 DOI:10.1007/s10291-011-0234-8
(  0) 0) |
| [3] |
Wang B, Miao L, Wang S, et al. A Constrained LAMBDA Method for GPS Attitude Determination[J]. GPS Solutions, 2009, 13(2): 97-107 DOI:10.1007/s10291-008-0103-2
(  0) 0) |
| [4] |
唐卫明, 孙红星, 刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J]. 武汉大学学报:信息科学版, 2005, 30(5): 444-446 (Tang Weiming, Sun Hongxing, Liu Jingnan. Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 444-446)
(  0) 0) |
| [5] |
Teunissen P J G. The Affine Constrained GNSS Attitude Model and Its Multivariate Integer Least-Squares Solution[J]. Journal of Geodesy, 2012, 86(7): 547-563 DOI:10.1007/s00190-011-0538-z
(  0) 0) |
| [6] |
Wang C. Development of a Low-Cost GPS-Based Attitude Determination System[D]. Calgary: University of Calgary, 2003
(  0) 0) |
| [7] |
欧吉坤, 王振杰. 单频GPS快速定位中模糊度解算的一种新方法[J]. 科学通报, 2003, 48(24): 2572-2575 (Ou Jikun, Wang Zhenjie. An Improved Regularization Method to Resolve Integer Ambiguity in Rapid Positioning Using Single Frequency GPS Receivers[J]. Chinese Science Bulletin, 2003, 48(24): 2572-2575 DOI:10.3321/j.issn:0023-074X.2003.24.016)
(  0) 0) |
| [8] |
Verhagen S, Teunissen P J G. The Ratio Test for Future GNSS Ambiguity Resolution[J]. GPS Solutions, 2013, 17(4): 535-548 DOI:10.1007/s10291-012-0299-z
(  0) 0) |
| [9] |
Luo X. Mathematical Models for GPS Positioning[M]. Berlin: Springer Berlin Heidelberg, 2013
(  0) 0) |
| [10] |
Luo N. Precise Relative Positioning of Multiple Moving Platforms Using GPS Carrier Phase Observables[J]. Adviser: Gerard Lachap, 2001, 62(12): 5601
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China
 2019, Vol. 39
2019, Vol. 39


