2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541004;
3. 广西壮族自治区地理信息测绘院,广西壮族自治区柳州市东环大道10号,545006
水汽主要分布在对流层底部,是大气层最活跃的成分,同时也是最难以描述的气象参数之一[1]。传统的水汽观测手段存在工作量大、设备昂贵和时空分辨率低等不足,随着GPS技术在空间天气监测的应用,极大地推动了GPS气象学的发展。利用GPS探测水汽可以很好地解决传统水汽探测能力的不足,因此,地基GPS反演大气水汽(precipitable water vapor, PWV)成为当前气象学的研究热点[2]。
在地基GPS反演PWV的过程中,转换系数K是一个极其关键的参数。PWV的计算通常由GPS卫星信号穿越大气层时的对流层天顶湿延迟(zenith wet delay, ZWD)乘以转换系数K得到。大气转换系数K值可利用探空站和大气再分析资料等气象参数通过积分法计算获取,但是该方法不能用于任意位置的K值计算。为此,文献[3]首次提出利用探空站资料建立加权平均温度(Tm)与地表温度(Ts)关系的模型,再通过将Tm值转换为K值来实现任意位置的K值计算。文献[4-5]在分析Tm与Ts、气压(Ps)和水汽压(es)关系的基础上,建立了适合中国大陆地区的Tm与Ts经验模型。文献[6-7]建立了局部的Tm与Ts模型。这些模型在计算K值时需要使用实测气象参数,从而限制了它们在实时GPS水汽探测上的应用。此外,由于Tm值具有显著的局地性和季节性,这些模型构建时未顾及K值的精细时空变化,因此在其他地区使用时会产生一定的偏差。为了满足实时GPS水汽探测的要求,诸多学者致力于非气象参数(Tm模型)K值模型的研究,并建立了一些全球性的和区域性的非气象参数(Tm模型)K值模型。如文献[8-9]利用探空站或大气再分析资料建立了几种全球非气象参数Tm模型,这些模型在全球取得了较好的精度,但是在局部地区的使用有待进一步验证。文献[10]利用全球几十个探空站的数据,建立一种顾及纬度和年周期的转换系数K值模型,在北美地区取得较好的效果。文献[11-12]对Emardson模型在中国低纬度地区和新疆地区的适用性进行了评估和精化。研究发现,Emardson模型在中国平缓地区可以获得较好的精度,但在地形起伏较大的地区预报精度有所降低,而精化后的模型精度可以得到较大改善。
我国西南地区属于亚热带季风气候,受东南风和西南风影响,夏季炎热多雨,冬季温和降水偏少。此外,西南地区地形起伏较大,探空站分布稀少且不均匀,导致该地区大部分区域水汽信息相对匮乏,而GPS水汽探测技术能较好地弥补这一不足,因此,研究西南地区GPS大气水汽转换系数模型的精化具有重要的现实意义。针对上述问题,本文利用中国西南地区19个探空站2011~2013年数据对Emardson模型进行精化,并对其在西南地区的适应性进行评估。
1 模型建立 1.1 K值积分计算本文采用积分法计算西南地区19个探空站2011~2014年的转换系数K[13]:
| $ K = {10^6}/{\rho _w}{R_v}\left( {{k_3}/{T_m} + {{k'}_2}} \right) $ | (1) |
式中,Rv为水汽气体常数;k′2、k3为大气折射常数;Tm为加权平均温度,其计算表达式为[14]:
| $ {T_{\rm{m}}} = \frac{{\int {\frac{{{P_v}}}{T}{\rm{d}}z} }}{{\int {\frac{{{P_v}}}{{{T^2}}}{\rm{d}}z} }} = \frac{{\sum {\frac{{{P_{vi}}}}{{{T_i}}}\Delta {h_i}} }}{{\sum {\frac{{{P_{vi}}}}{{T_i^2}}\Delta {h_i}} }} $ | (2) |
式中,Pvi为第i层大气的平均水汽压,Ti为第i层大气的平均温度,Δhi为第i层大气的厚度。
1.2 精化模型表达式Emardson等[10]利用全球数十个探空站数据,建立了一种顾及纬度和年周期变化的大气水汽转换系数K值模型(简称Emardson模型)。该模型基本采用北美地区的探空站数据,因此在北美地区能够取得较好的效果。由于Emardson模型较简单,只与纬度和年积日有关,是一个非气象参数模型,且能保证较高的精度,因此其在GPS实时水汽反演中具有较大的应用潜力。文献[11-12]对Emardson模型在中国低纬度地区和新疆地区进行精化,精化后的Emardson模型取得了较好的结果。由于西南地区地形起伏较大,探空站分布稀少且不均匀,因此可利用GPS水汽探测来弥补这一不足。本文探索在我国西南地区对Emardson模型进行精化,最终得到两个精化模型:不考虑地形起伏影响的Emardson-I模型,该模型是基于转换系数K在时空特性上与测站纬度、年积日的相关性而建立的周期性三角函数模型,见式(3);文献[11-12]表明,K值的变化与高程存在一定的相关性,因此,在式(3)的基础上考虑地形起伏的影响,进而建立顾及地形起伏的Emardson-H模型,见式(4):
| $ \begin{array}{*{20}{c}} {K = {\alpha _0} + {\alpha _1}\varphi + {\alpha _2}\sin \left( {2{\rm{ \mathsf{ π} }}\frac{{{\rm{doy}}}}{{365.25}}} \right) + }\\ {{\alpha _3}\cos \left( {2{\rm{ \mathsf{ π} }}\frac{{{\rm{doy}}}}{{365.25}}} \right)} \end{array} $ | (3) |
| $ \begin{array}{*{20}{c}} {K = {\alpha _0} + {\alpha _1}\varphi + {\alpha _2}\sin \left( {2{\rm{ \mathsf{ π} }}\frac{{{\rm{doy}}}}{{365.25}}} \right) + }\\ {{\alpha _3}\cos \left( {2{\rm{ \mathsf{ π} }}\frac{{{\rm{doy}}}}{{365.25}}} \right) + {\alpha _4}H} \end{array} $ | (4) |
式中,φ为大地纬度, doy为年积日, H为海拔, α0、α1、α2、α3、α4为模型系数。
2 结果分析 2.1 精度评估指标本文采用平均绝对偏差(MAE)和均方根误差(RMS)两种指标来评价模型的精度,其表达式为:
| $ {\rm{MAE = }}\frac{1}{N}\sum\limits_{i = 1}^N {\left| {X_{\rm{M}}^i - X_{\rm{R}}^i} \right|} $ | (5) |
| $ {\rm{RMS = }}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {X_{\rm{M}}^i - X_{\rm{R}}^i} \right)}^2}} } $ | (6) |
式中,N表示数据样本数,XMi表示第i个模型计算值,XRi表示第i个模型参考值。
2.2 数据来源分析本文研究使用的数据为中国西南地区19个探空站2011~2014的探空数据,19个探空站分布如图 1,各区域划分及各站相关信息见表 1。相关研究表明,大气转换系数K(Tm)与纬度和高程表现出较强的相关性[2, 11]。为了探讨高程因子对K值模型的影响,本文根据探空站的地域分布特征,选取纬度相近、地形起伏较为平缓的广西、贵州及云南地区作为区域1,另外选取纬度相近、地形起伏较大的长江中上游、西藏及青海南部区域作为区域2,并对这两个区域K值进行时空分布特性分析。此外,均匀选取中国西南地区的12个探空站(包括区域1的桂林、南宁、贵阳、昆明、蒙自、腾冲,区域2的重庆、温江、西昌、拉萨、昌都、玉树)作为模型系数计算的内部站,另选取7个探空站(包括梧州、百色、思茅、威宁、甘孜、恩施、那曲)作为模型检核的外延站。利用积分法计算12个内部站2011~2013年K值,并分别建立整个中国西南地区不考虑地形起伏的K值模型(简称Emardson-I模型)和顾及地形起伏的K值模型(简称Emardson-H模型),利用最小二乘法求解这两个模型系数,进而利用这两个模型预报中国西南地区19个探空站2014年K值,对比分析Emardson-I模型和Emardson-H模型在中国西南地区预报K值的适用性。
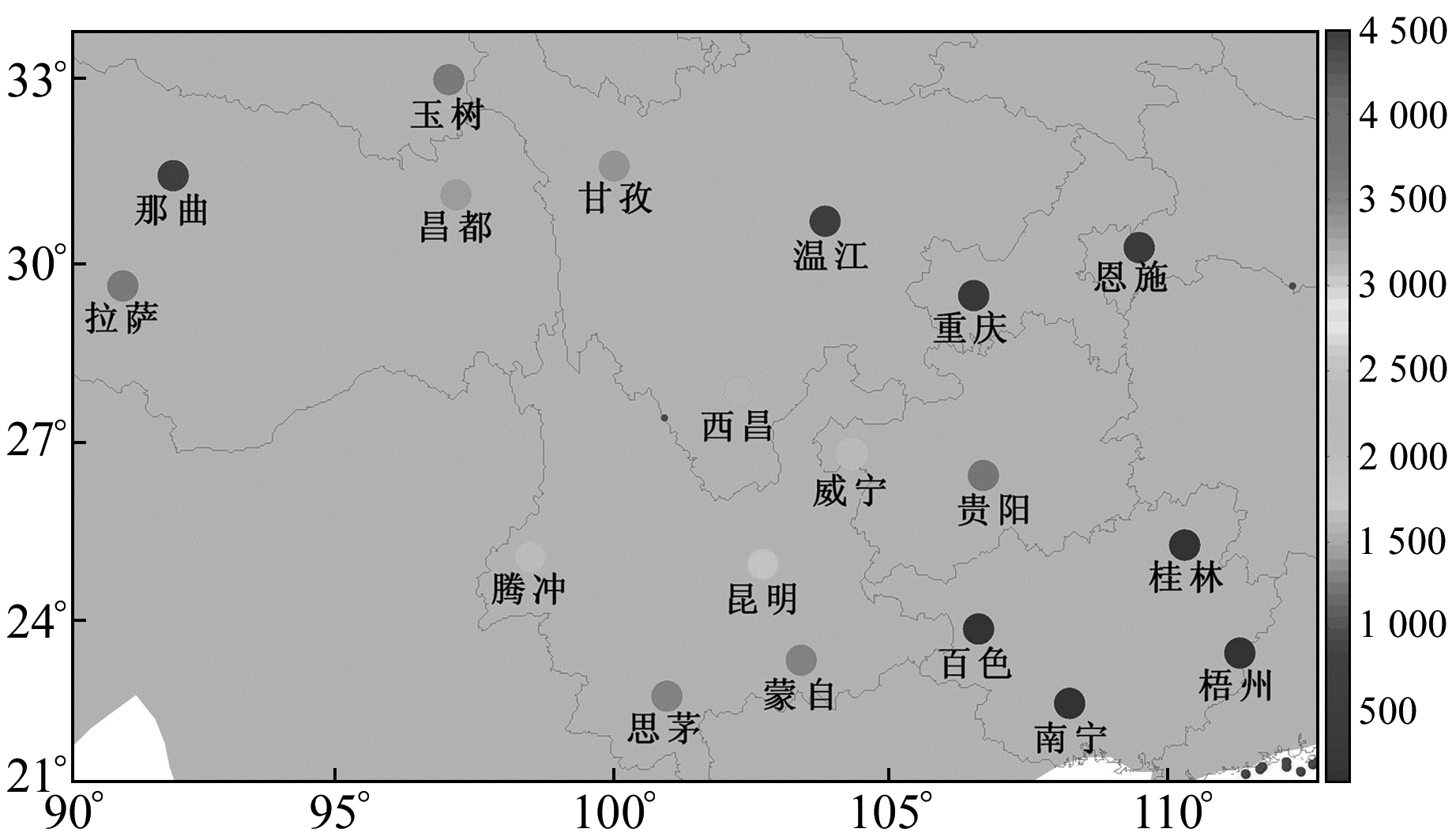
|
图 1 中国西南地区19个探空站地理位置分布 Fig. 1 Distribution of 19 radiosonde stations over southwest China |
|
|
表 1 中国西南地区19个探空站区域划分及各站信息情况 Tab. 1 Regionalization of 19 radiosonde stations and its information over southwest China |
利用积分法计算的12个内部站2011~2013的K值,根据最小二乘法分别求解式(3)、式(4),得到Emardson-I模型和Emardson-H模型的模型系数,如表 2所示。
|
|
表 2 Emardson-I模型和Emardson-H模型的模型系数 Tab. 2 Model coefficients of both Emardson-I model and Emardson-H model |
由表 2可知,在整个中国西南地区,K值随纬度升高而减小的速率约为0.000 97,K值随海拔上升而降低的递减系数为-0.000 002 4。因此,在地形起伏较平缓的地区,K值受海拔影响较小,可忽略不计;在高海拔地区,海拔对K值的影响不可忽视,特别是在地形起伏较大的中国西南地区,最大高差达4 000 m以上。
利用上述所求的Emardson-I模型和Emardson-H模型分别预报2014年19个站的K值,其结果如图 2和图 3所示。
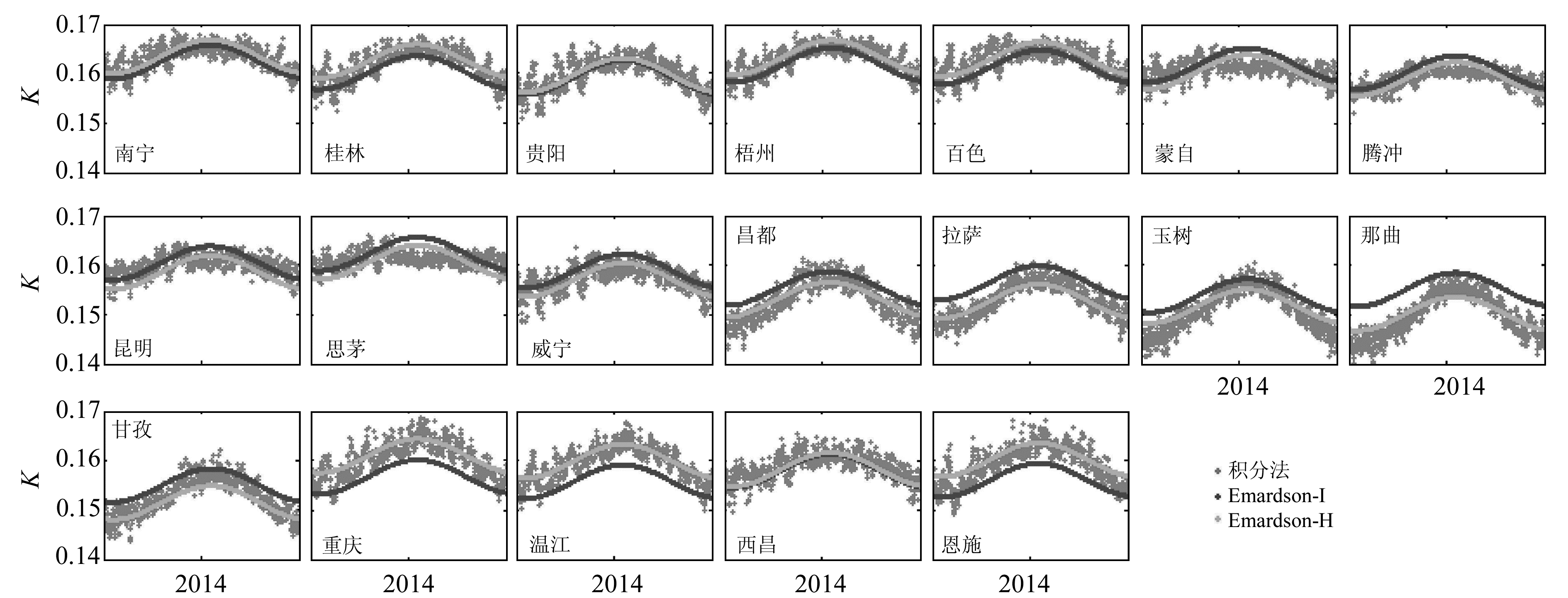
|
图 2 Emardson-H模型与Emardson-I模型的预报效果对比 Fig. 2 Prediction comparison of both Emardson-I model and Emardson-H model |

|
图 3 Emardson-H模型与Emardson-I模型预报19个站2014年K值的RMS和MAE精度分布情况 Fig. 3 Prediction K values of MAE and RMS of both Emardson-I and Emardson-H models in 2014 among 19 radiosonde stations |
由图 2可知,Emardson-I预报的K值与积分法计算的K值在低海拔地区偏差较小,在高海拔地区偏差较大;而顾及地形起伏的Emardson-H模型在中国西南地区预报K值的整体情况均优于Emardson-I模型,特别是在地形起伏大的区域2,Emardson-I预报的K值出现较大偏差,而Emardson-H模型预报的K值与积分法计算的K值符合较好。
由图 3可知,顾及地形起伏的Emardson-H模型整体上较Emardson-I有显著的提高,相对于Emardson-I模型,Emardson-H模型的MAE减少了34.6%,RMS减少了34.5%。在海拔较低和地形起伏较为平缓的区域1,Emardson-H模型相对于Emardson-I模型的预报精度提升较小;而在地形起伏大的区域2,Emardson-H模型相对于Emardson-I模型的预报精度提升较显著,特别是区域2的低海拔地区重庆、温江站和高海拔地区的拉萨、那曲站。此外,利用Emardson-H模型进行K值预报,无论是对于参与建模的12个内部站,还是未参与建模的7个外延站,两种情况下预报的RMS都比较接近,分别为0.002 02和0.002 08。由此说明,本次构建的Emardson-H模型在中国西南地区具有较好的适用性。表 3给出Emardson-I模型和Emardson-H模型在不同划分区域的精度及Emardson-H模型相对于Emardson-I模型在西南地区的总体精度提升情况。
|
|
表 3 Emardson-I与Emardson-H预报两个区域2014年K值的精度对比 Tab. 3 Precision comparison of K values between Emardson-I and Emardson-H models in 2014 over two regions |
由表 3可知,相对于Emardson-I模型,Emardson-H模型在中国西南地区适应性明显提高,尤其是地形起伏较大的区域2,其预报的MAE和RMS精度分别为0.001 64和0.002 05,较Emardson-I模型分别提高了50.5%和46.9%;在地形较平缓的区域1,Emardson-H模型预报精度比Emardson-I模型提高了8%以上。因此,在地形起伏程度不同的区域1和区域2,顾及海拔的Emardson-H模型均表现出良好的稳定性。
此外,图 4给出两个模型预报年均K值的变化趋势。由图可以看出,即便在地形起伏较为平缓的区域1,Emardson-I预报的年均K值也存在一定的偏差,在地形起伏较大的区域2,其预报偏差更加显著,与积分法计算的年均K值的相关系数只有0.82;而Emardson-H模型预报2014年的年均K值与积分法计算的2014年年均K值在整个中国西南地区均吻合较好,两者的相关系数达0.99。由此可知,高程是影响K值预报的一个重要影响因子,尤其在高海拔地区。因此,在构建K值模型时,建议顾及高程的变化,从而提高K值预报的精度和稳定性。
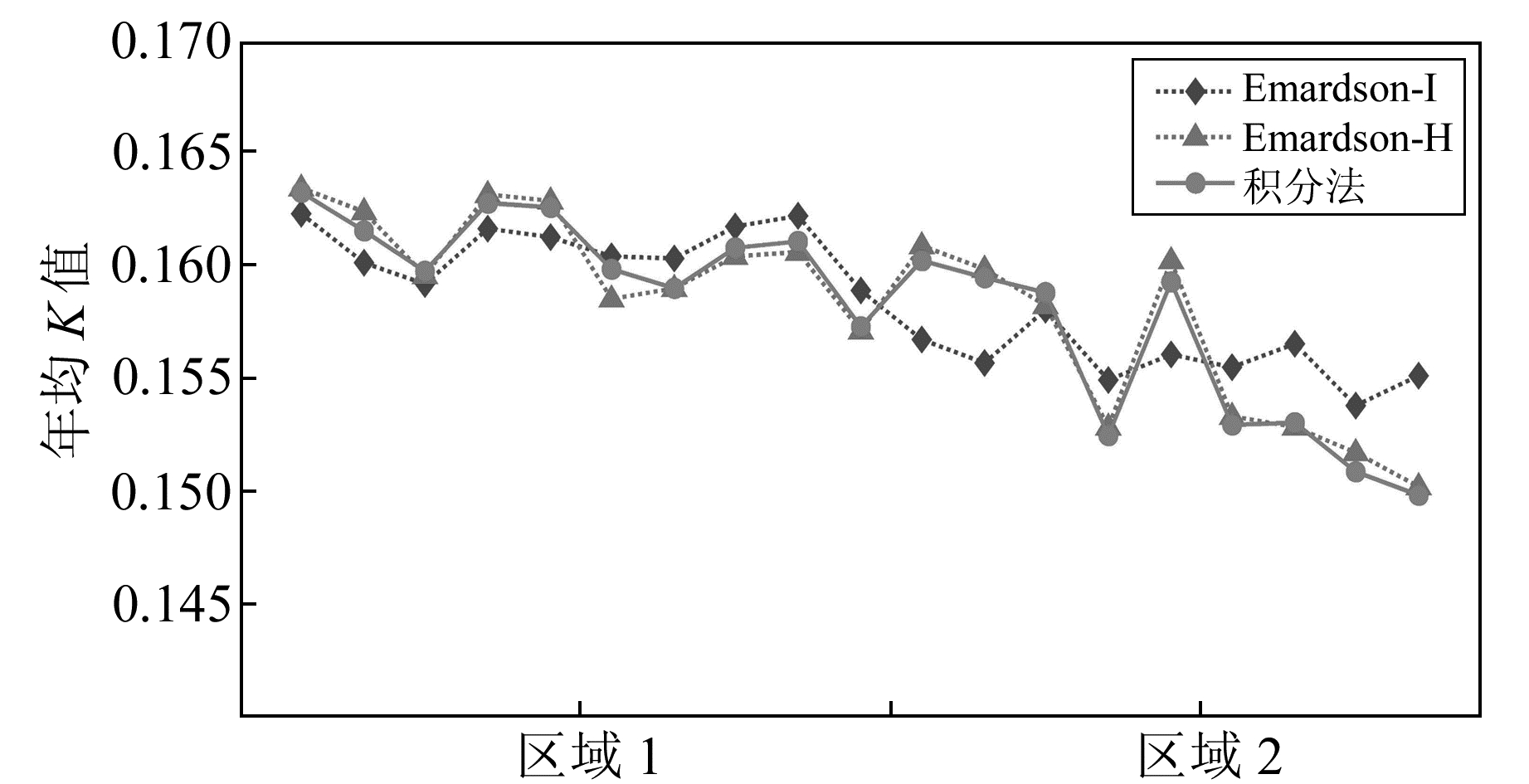
|
图 4 Emardson-I模型与Emardson-H模型预报2014年年均K值情况 Fig. 4 Annual prediction K values between Emardson-I and Emardson-H models in 2014 |
为了验证本文提出的两种新模型在GPS大气水汽(PWV)中的反演精度,本文选取位于拉萨的中国陆态网拉萨站2015年GPS-ZTD(zenith total delay, 天顶总延迟)数据和探空站2015年的PWV、地表温度、地表气压数据进行实例分析,由于拉萨GPS站与探空站之间的距离较近且高差较小,因此可以减少GPS站计算PWV与探空站PWV之间的差异,提高检验的可靠性。中国陆态网提供的GPS-ZTD数据时间分辨率为1 h,而探空站提供的PWV时间分辨率为12 h,故首先对两种数据在时间上进行重采样,获得24 h分辨率的数据,便于检验分析。
本文采用Saastamoinen模型进行对流层天顶干延迟(zenith hydrostatic delay, ZHD)计算,从而获得天顶对流层湿延迟(ZWD),进而计算出GPS-PWV,GPS-PWV计算的原理详见文献[15]。为了检验Emardson-H模型与Emardson-I模型应用于PWV计算的精度,以位于高海拔地区的拉萨GPS基准站为例进行GPS-PWV反演,以相距较近的探空站提供的PWV数据为参考值,检验PWV计算精度,同时与广泛应用的Bevis模型进行对比分析(图 5)。
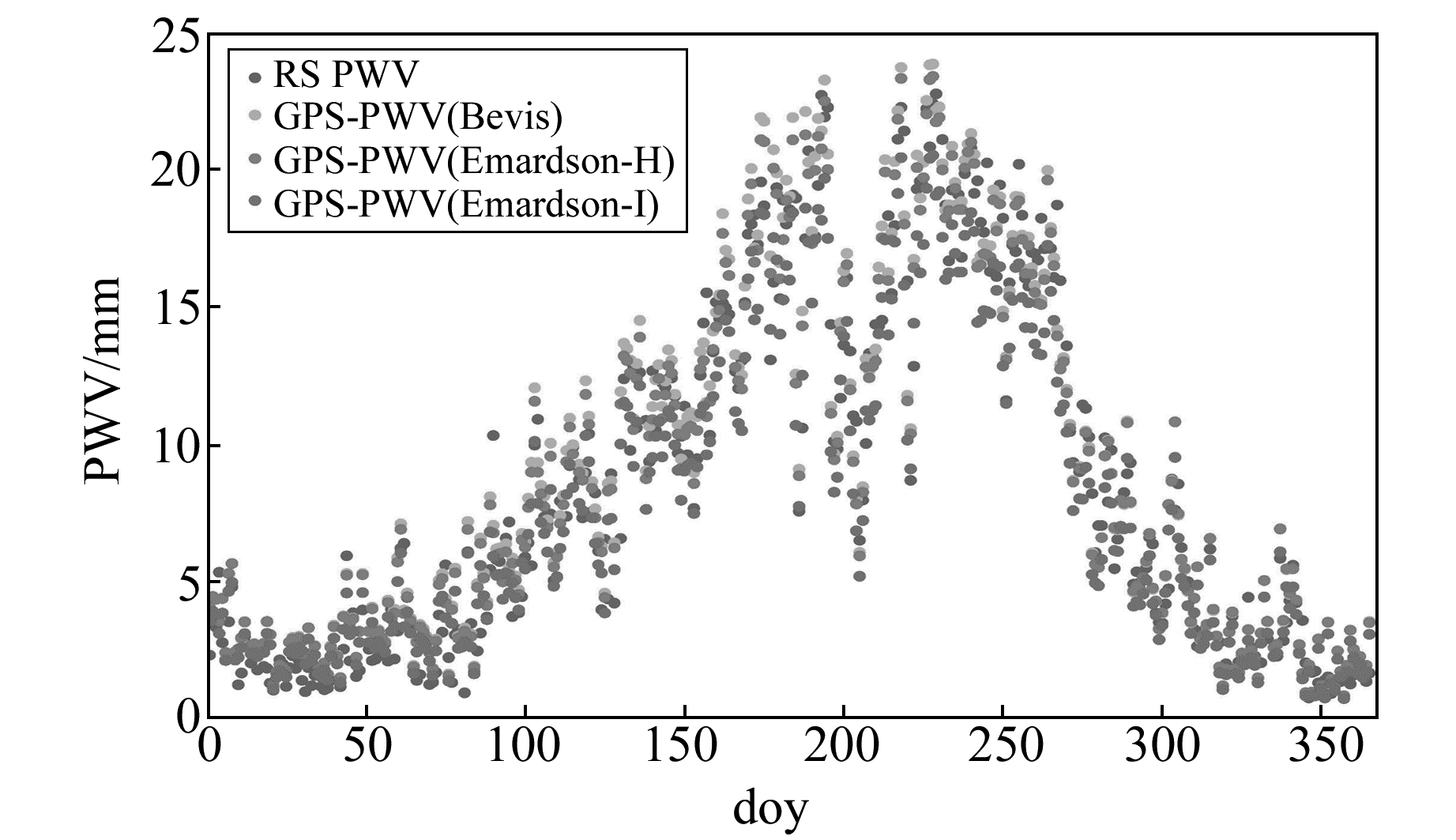
|
图 5 不同模型反演的拉萨站GPS-PWV值与探空站PWV结果比较 Fig. 5 GPS-PWVs derived from different models compared with PWV derived from radiosonde at Lhasa station |
由图 5可以看出,利用不同的大气转换系数模型(加权平均温度模型)进行拉萨站GPS-PWV反演,其反演结果与探空站水汽具有较好的一致性,其年均精度如表 4所示。
|
|
表 4 不同模型反演的拉萨站GPS-PWV值精度对比 Tab. 4 Precision comparison of different models for deriving GPS-PWV at Lhasa station |
由表 4可知,Emardson-H模型可获得最优的GPS-PWV计算精度。相对于其他两种模型,Emardson-I模型精度最差,主要原因是拉萨站属于高海拔地区,Emardson-I模型未顾及高程的影响;Bevis模型虽然未顾及高程影响,但模型利用了实测的地表温度,故亦能使Bevis模型保持良好的GPS-PWV反演精度。尽管如此,在拉萨站Emardson-I模型反演GPS-PWV的精度仍然优于2 mm。由于Emardson-H模型不需要气象参数且能保持较高的精度,因此在缺乏气象参数的高海拔地区,建议使用Emardson-H模型进行GPS-PWV反演。
3 结语利用中国西南地区2011~2013年19个探空站数据积分计算的K值,分别建立中国西南地区Emardson模型的两个精化模型:Emardson-I模型(未顾及高程因子)和Emardson-H模型(顾及高程因子)。利用2014年19个探空站积分计算的K值对两个精化模型进行预报,验证其预报精度。相对于Emardson-I模型,无论在地形平缓地区还是高海拔地区,Emardson-H模型均表现出更好的适应性,其与积分K值的相关系数高达0.99,但是在地形平缓地区的改善不够显著,总体上Emardson-H模型在整个中国西南地区能够获得较好的精度和稳定性。对于Emardson-I模型,在地形平缓地区,其可以获得较好的K值预报效果,但是在高海拔地区,由于未顾及高程的变化,该模型产生了较大的偏差,表现出较差的适应性。因此,在构建K值模型时,建议顾及高程的变化。此外,将构建的两种新模型用于GPS-PWV反演,结果表明Emardson-H模型仍能取得最优的GPS-PWV反演结果;尽管Emardson-I模型的反演结果低于Emardson-H模型,其GPS-PWV反演精度仍能优于2 mm。由于Emardson-H模型不需要实测气象参数,因此在中国西南地区,尤其是在无气象参数的地区,进行GPS-PWV反演具有较大的应用潜力。
| [1] |
Rocken C, Hove T, Ware R. Near Real-Time GPS Sensing of Atmospheric Water Vapor[J]. Geophys Res Lett, 1997, 24: 3221-3224 DOI:10.1029/97GL03312
(  0) 0) |
| [2] |
姚宜斌, 张豹, 许超钤, 等. Tm-Ts的相关性分析及全球纬度相关的线性关系模型构建[J]. 科学通报, 2014, 59: 816-824 (Yao Yibin, Zhang Bao, Xu Chaoqian, et al. Analysis of the Global Tm-Ts Correlation and Establishment of the Latitude-Related Linear Model[J]. China Sci Bull, 2014, 59: 816-824)
(  0) 0) |
| [3] |
Bevis M, Businger S, Herring T A. GPS Meteorology: Remote Sensing of Atomspheric Water Vapor Using the Global Positioning System[J]. J Geophys Res, 1992, 88: 15787-15801
(  0) 0) |
| [4] |
李建国, 毛节泰, 李成才. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J]. 气象学报, 1999, 57(3): 283-292 (Li Jianguo, Mao Jietai, Li Chengcai. The Approach to Remote Sensing of Water Vapor Based on GPS Linear Regression Tm in Eastern Region of China[J]. Acta Meteorol Sin, 1999, 57(3): 283-292 DOI:10.3969/j.issn.1001-7313.1999.03.004)
(  0) 0) |
| [5] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 412-416 (Wang Xiaoying, Dai Ziqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416)
(  0) 0) |
| [6] |
Wang Y, Liu Y P, Liu L T, et al. Retrieval of the Change of Precipitable of Water Vapor by GPS Technique[J]. Geo-Spatial Information Science, 2007, 10(4): 265-268
(  0) 0) |
| [7] |
于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报:信息科学版, 2009, 34(6): 741-744 (Yu Shengjie, Liu Lintao. Validation and Analysis of the Water-Vapor-Weighted Mean Temperature from Tm-Ts Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741-744)
(  0) 0) |
| [8] |
Yao Y B, Zhu S, Yue S Q. A Globally Applicable, Season-Specific Modle for Estimating the Weighted Mean Temperature of the Atmosphere[J]. J Geod, 2012, 86: 1125-1135 DOI:10.1007/s00190-012-0568-1
(  0) 0) |
| [9] |
陈鹏, 陈家君. 利用NCEP再分析资料建立全球大气加权平均温度模型[J]. 大地测量与地球动力学, 2014, 34(3): 133-141 (Chen Peng, Chen Jiajun. Establishment of Global Atmospheric Weighted Average Temperature Model Using NCEP Reanalysis Data[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 133-141)
(  0) 0) |
| [10] |
Emardson T R, Derks H J P. On the Relation between the Wet Delay and the Intergrated Precipitable Water Vapor in Euroupean Atmosphere[J]. Meteorol Appl, 2000(7): 61-68
(  0) 0) |
| [11] |
姚朝龙, 罗志才, 刘立龙, 等. 顾及地形起伏的中国低纬度地区湿延迟与可降水量转换关系研究[J]. 武汉大学学报:信息科学版, 2015, 40(7): 907-912 (Yao Chaolong, Luo Zhicai, Liu Lilong, et al. On the Relation between the Wet Delay and the Water Precipitable Vapor in Consideration of Topograghic Relief in the Low-Latitude Region of China[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 907-912)
(  0) 0) |
| [12] |
刘立龙, 陈香萍, 封海洋, 等. 新疆地区Emardson大气水汽转换系数适用性分析[J]. 大地测量与地球动力学, 2016, 36(5): 434-437 (Liu Lilong, Chen Xiangping, Feng Haiyang, et al. Analysis of the Applicability of the Emardson Model for Transformation Coefficient of Water Vapor in the Region of Xinjiang[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 434-437)
(  0) 0) |
| [13] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. J Appl Meteorol, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [14] |
Davis J, Herring T, Shapiro I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Sci, 1985, 20(6): 1593-1607 DOI:10.1029/RS020i006p01593
(  0) 0) |
| [15] |
Huang L K, Liu L L, Yao C L. A Zenith Tropospheric Delay Correction Model Based on the Regional CORS Network[J]. Geodesy and Geodynamics, 2012, 3(4): 53-62 DOI:10.3724/SP.J.1246.2012.00053.1
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541004, China;
3. Institute of Geoinformation and Geomatics of Guangxi Zhuang Autonomous Region, Liuzhou 545006, China
 2019, Vol. 39
2019, Vol. 39


