在卫星钟性能分析方面,学者们进行了大量研究[1-4],但这些研究存在一定的局限性。首先,大部分研究是针对GPS系统进行的,基于北斗系统卫星钟的十分有限;其次,针对北斗二号卫星钟评估的研究大多是在卫星在轨运行初期、中期进行的;最后,已有的原子钟性能评估体系还不够全面,研究内容和结论大多集中在卫星钟的某一特性上。
本文选取长期在轨运行且即将到设计运行寿命的GEO-1卫星[5-6]和其他轨道类型的IGSO-3、MEO-4卫星作为评估对象,基于GEO-1卫星2017-05-01~10-31(处于设计寿命末年)、IGSO-3和MEO-4卫星2017-10-01~10-31的星地双向无线电比对钟差数据进行频率准确度、稳定度和漂移率的综合评估和分析,得到一些有益的新结论,可为北斗全球卫星导航系统的建设、维护提供参考和借鉴。
1 卫星钟频率准确度、稳定度、漂移率计算方法 1.1 频率准确度频率准确度是指频率源的实际频率值与其标称值之间的相对偏差,在实际测量过程中是以参考频标的实际频率值作为标准,这就要求参考频标的准确度至少比被测频率源高一个量级。通过星地双向无线电时间比对法获得卫星钟差ΔtAB(相位数据),将ΔtAB记为xi(i=1, 2, …, N),N为取样个数。设取样间隔为τ,对钟差数据进行粗差剔除处理(可采用中位数粗差探测法),然后进行最小二乘拟合[1]:
| $ x\left( t \right) = \bar x + {K_\tau }\left( {t - \bar t} \right) $ | (1) |
式中,
考虑到频率漂移的影响,应控制取样间隔(不宜太长)。取τ=1 d,对所有测量数据作线性拟合后得到钟差序列
| $ A = \frac{{\hat x\left( {t + \tau } \right) - \hat x\left( t \right)}}{\tau } $ | (2) |
通过上述方法得到的是卫星钟对系统的相对频偏,由于系统频标的准确度比卫星钟高(至少一个数量级),可将该相对频偏作为卫星钟的频率准确度。计算得到多个(设为M个)平均频率偏差{Aj, j=1, 2, …, M},取max{Aj, j=1, 2, …, M}作为整个评估时段的最终结果,以此实现频率准确度的测定[2]。
1.2 频率稳定度从时域上分析卫星钟频率稳定度主要利用Allan系列方差和Hadamard系列方差。Allan方差容易受到线性频漂的影响,适用于分析频漂不明显的铯原子钟;Hadamard方差通过时差数据的三阶差分计算(频率数据为二阶差分)去除线性频漂影响,适用于频漂比较明显的铷原子钟。由于北斗二号在轨卫星配备的是铷原子钟,其短期稳定度较好,但频率漂移率较大,相对来讲,Hadamard系列方差更适合分析北斗卫星钟频率稳定性[3]。
对于时差(相位)数据,Hadamard方差定义如下:
| $ \begin{array}{*{20}{c}} {H\sigma _y^2\left( \tau \right) = {\rm{ }}\frac{1}{{6{\tau ^2}\left( {N - 3} \right)}} \cdot }\\ {\sum\limits_{i = 1}^{N - 3} {{{\left[ {{x_{i + 3}} - 3{x_{i + 2}} + 3{x_{i + 1}} - {x_i}} \right]}^2}} } \end{array} $ | (3) |
对于时差(相位)数据,重叠Hadamard方差(overlapping hadamard variance, OHV)定义如下:
| $ \begin{array}{*{20}{c}} {H\sigma _y^2\left( \tau \right) = {\rm{ }}\frac{1}{{6{\tau ^2}\left( {N - 3m} \right){\tau ^2}}} \cdot }\\ {\sum\limits_{i = 1}^{N - 3m} {{{\left[ {{x_{i + 3m}} - 3{x_{i + 2m}} + 3{x_{i + 1m}} - {x_i}} \right]}^2}} } \end{array} $ | (4) |
式中,τ=mτ0为平滑时间,τ0为基本取样间隔,m为平滑因子,xi为时差(相位)数据,N为xi的个数。
1.3 频率漂移率由于卫星钟在空间环境中长期连续运行,在此过程中卫星钟受到内部元器件参数变化及外部环境的影响,其输出频率值会随时间变化呈现出线性单调增加或减小,这种线性率称为频率漂移率。对于高稳石英晶体频标,通常称其漂移率为老化率[1]。
基于频率源在时域上实际输出的相对频率值数据,通过最小二乘法计算得到频率漂移率:
| $ D = \frac{{\sum\limits_{i = 1}^N {\left( {{y_i} - \bar y} \right)\left( {{t_i} - \bar t} \right)} }}{{\sum\limits_{i = 1}^N {{{\left( {{t_i} - \bar t} \right)}^2}} }} $ | (5) |
式中,
综合考虑北斗卫星轨道类型、星地比对钟差数据的观测时间、星载主钟情况等因素,选取北斗二号在轨卫星GEO-1、IGSO-3和MEO-4的星载主钟作为评估对象,利用星地无线电双向钟差数据计算卫星钟的频率稳定度、准确度和漂移率等性能指标,由此分析研究得出评估结论。
由于GEO-1卫星在所有北斗二号在轨卫星中运行时间最长且即将到设计运行寿命,其运行状况和性能指标的评估结果具有重要意义,故将其作为重点评估对象。评估时段选取连续的6个月,其他2颗非静止轨道卫星的评估时段选取1个月。钟差数据的时间长度如下:
GEO-1卫星:2017-05-01~05-31,2017-06-01~06-30,2017-07-01~07-31,2017-08-01~08-31,2017-09-02~09-30,2017-10-01~10-31(由于2017-09-01数据质量较差,将其整日数据剔除);
IGSO-3卫星:2017-10-01~10-31;
MEO-4卫星:2017-10-01~10-31。
2.1 实验数据质量分析以2017-08~09 GEO-1卫星和2017-10 IGSO-3卫星、MEO-4卫星的钟差数据为例进行分析,其余时段数据不再以图像形式详细列出。以上选定的卫星及其时间段剔除粗差值后的钟差数据如图 1~8所示。
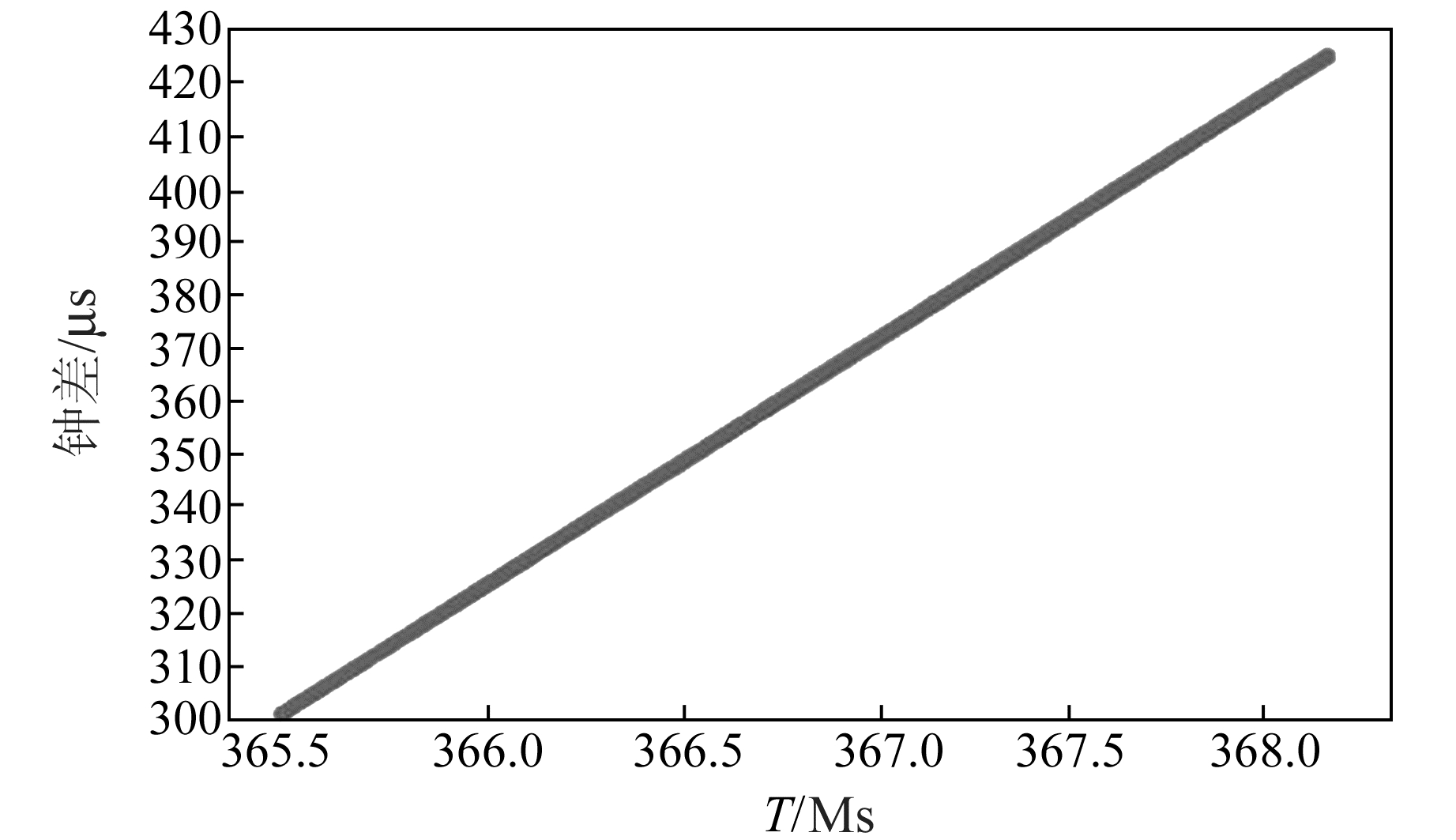
|
图 1 GEO-1钟差数据(8月) Fig. 1 Clock bias of GEO-1(August) |
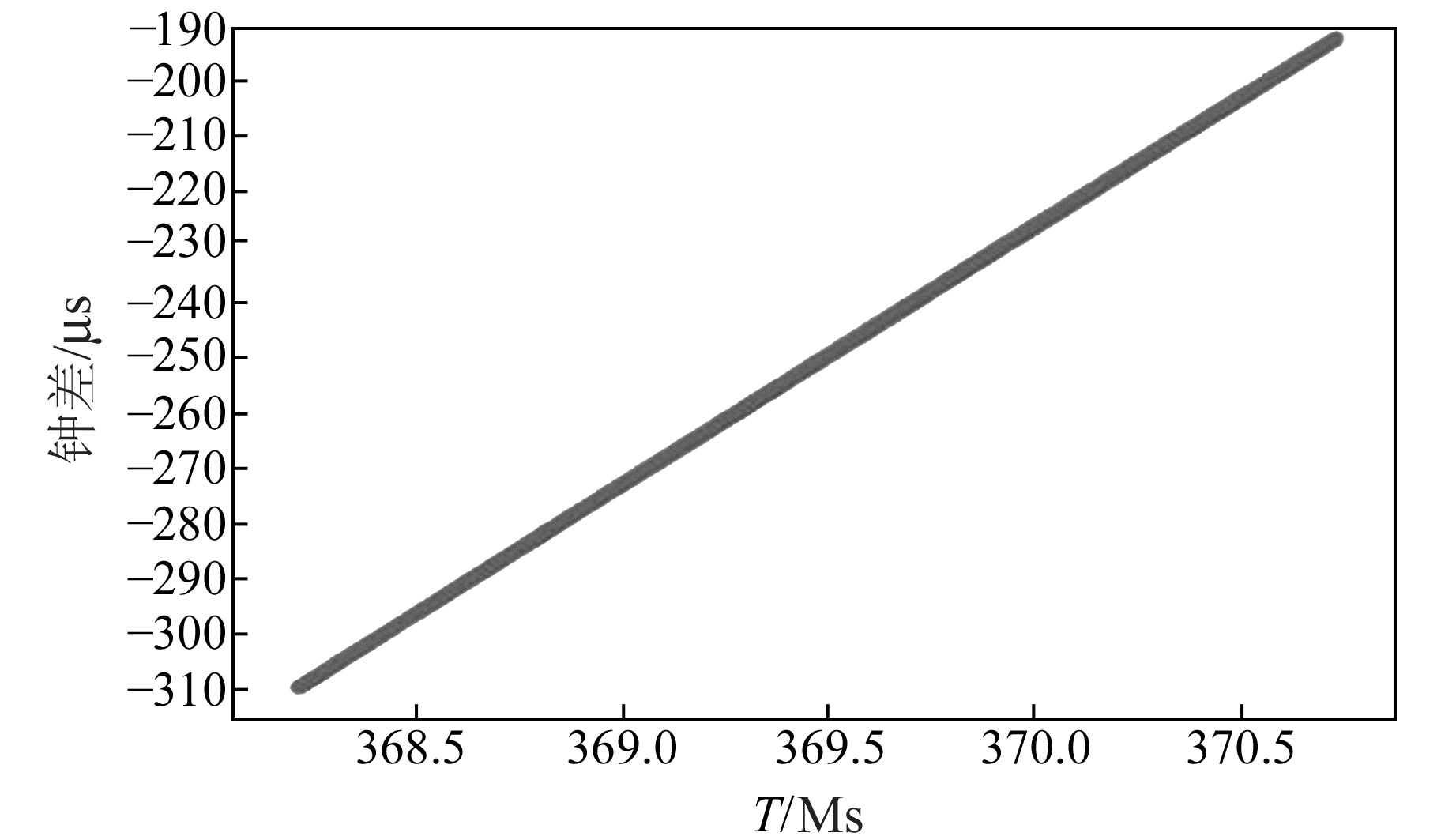
|
图 2 GEO-1钟差数据(9月) Fig. 2 Clock bias of GEO-1(September) |
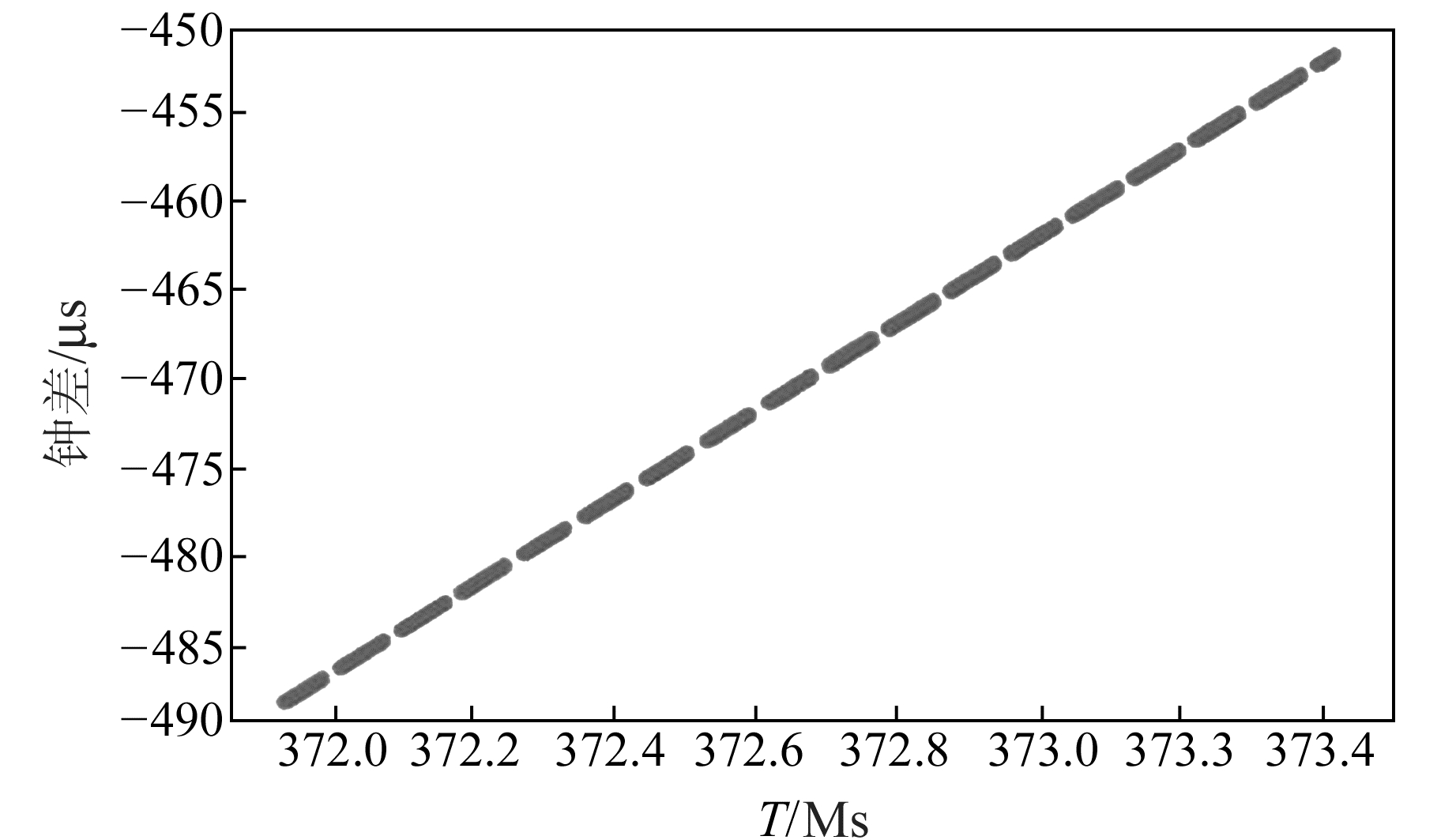
|
图 3 IGSO-3钟差数据(10月) Fig. 3 Clock bias of IGSO-3(October) |
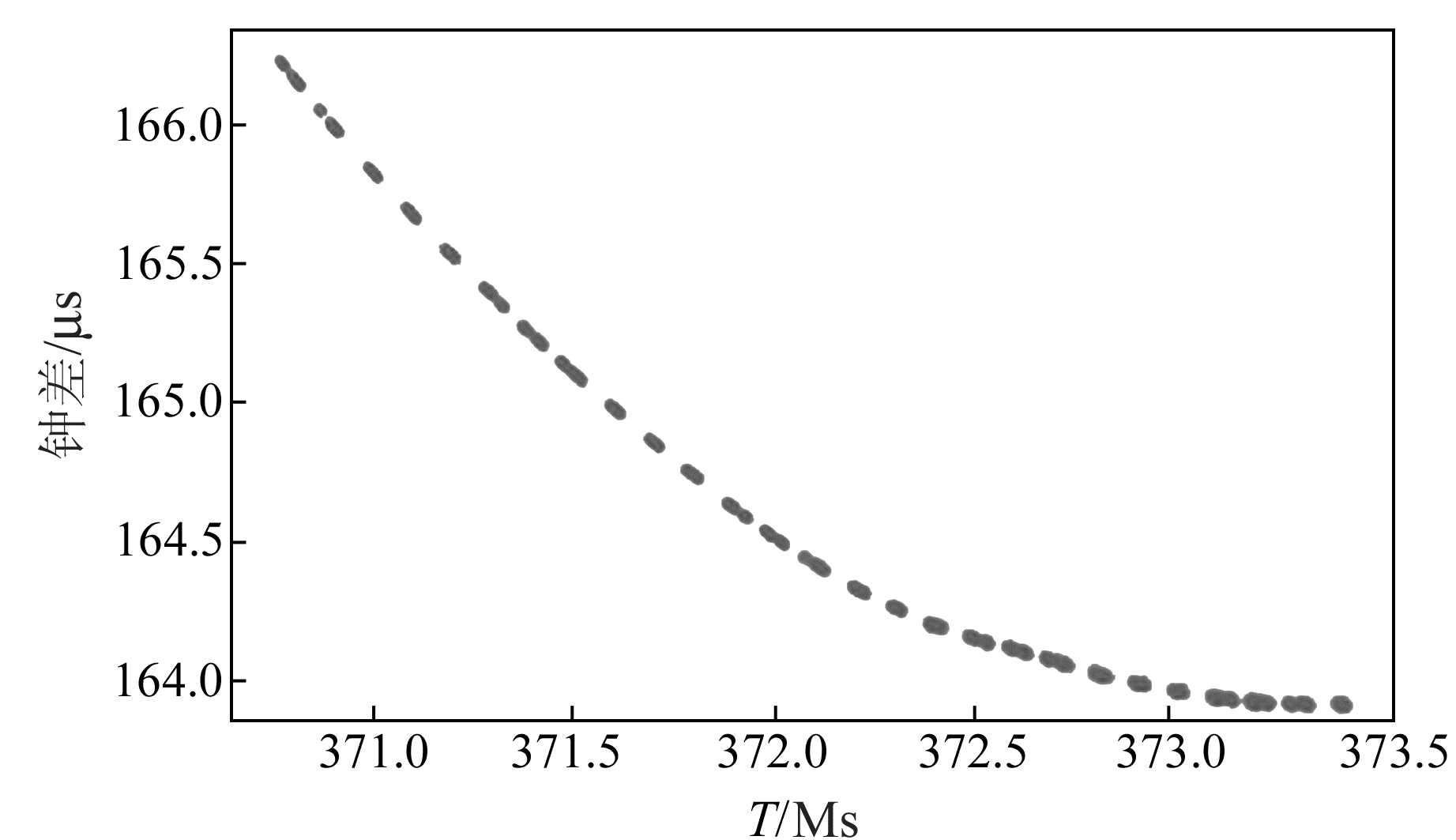
|
图 4 MEO-4钟差数据(10月) Fig. 4 Clock bias of MEO-4(October) |
|
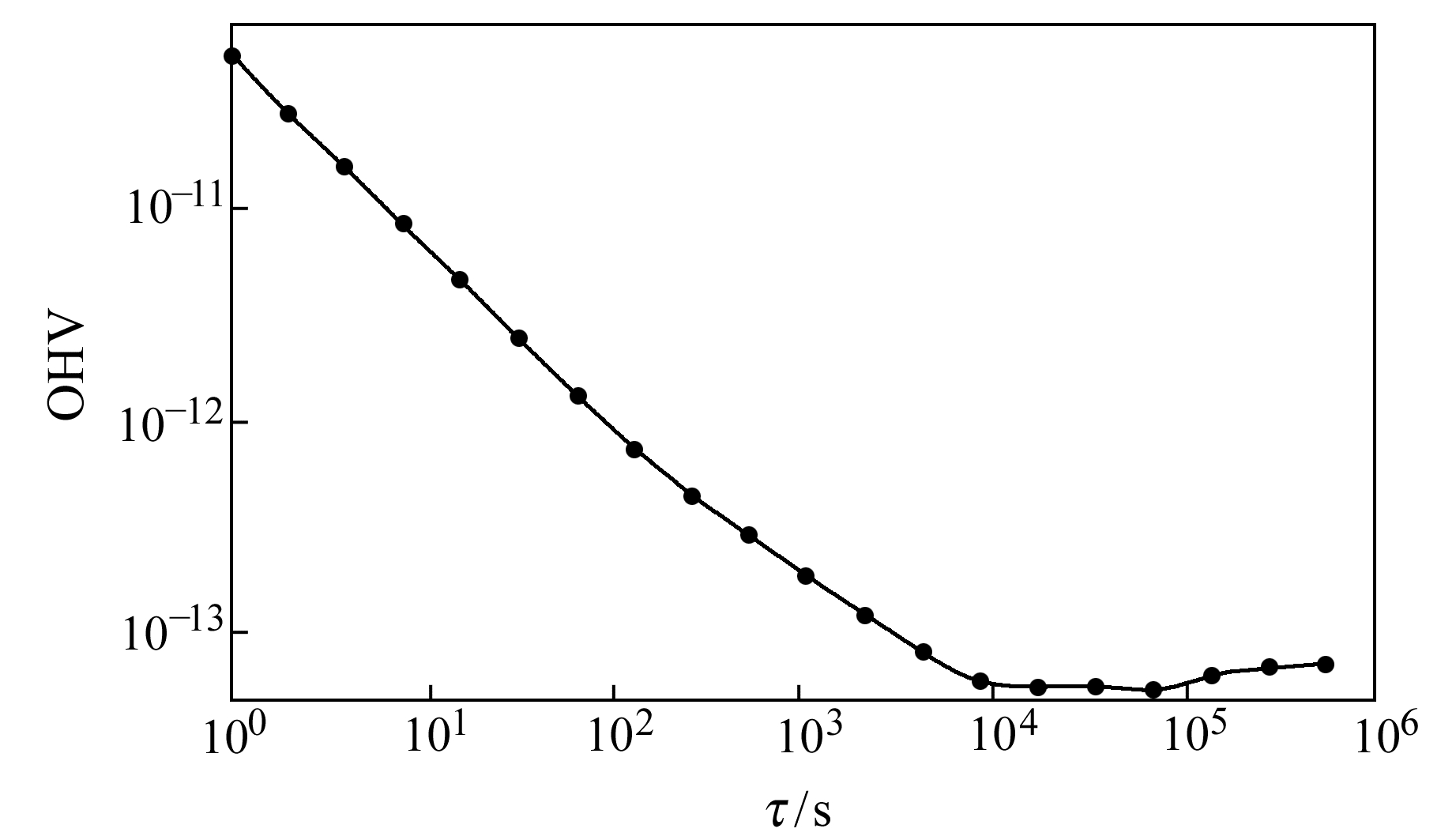
图 5 GEO-1 OHV数据(8月) Fig. 5 OHV of GEO-1(August) |
|
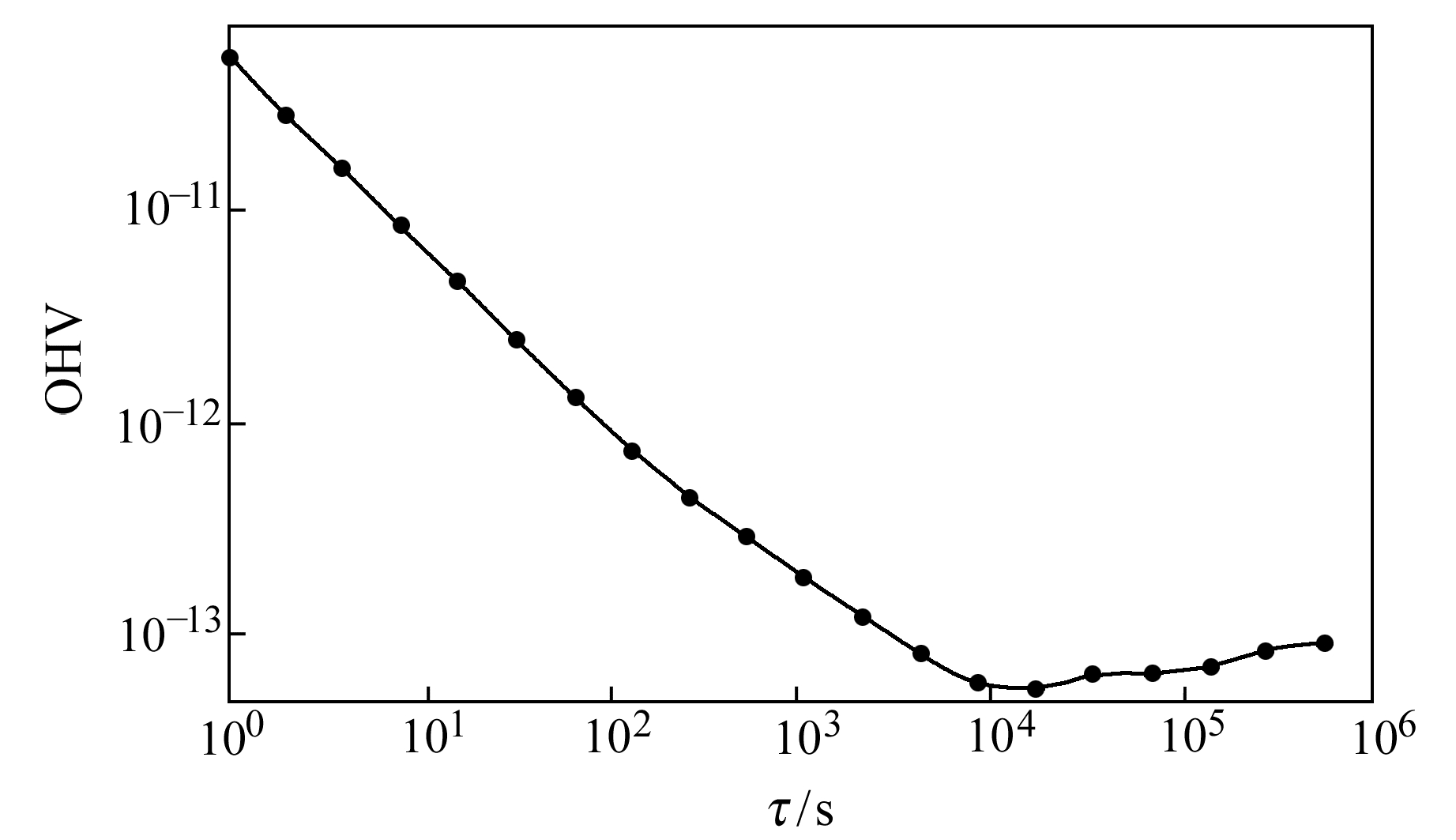
图 6 GEO-1 OHV数据(9月) Fig. 6 OHV of GEO-1(September) |
|
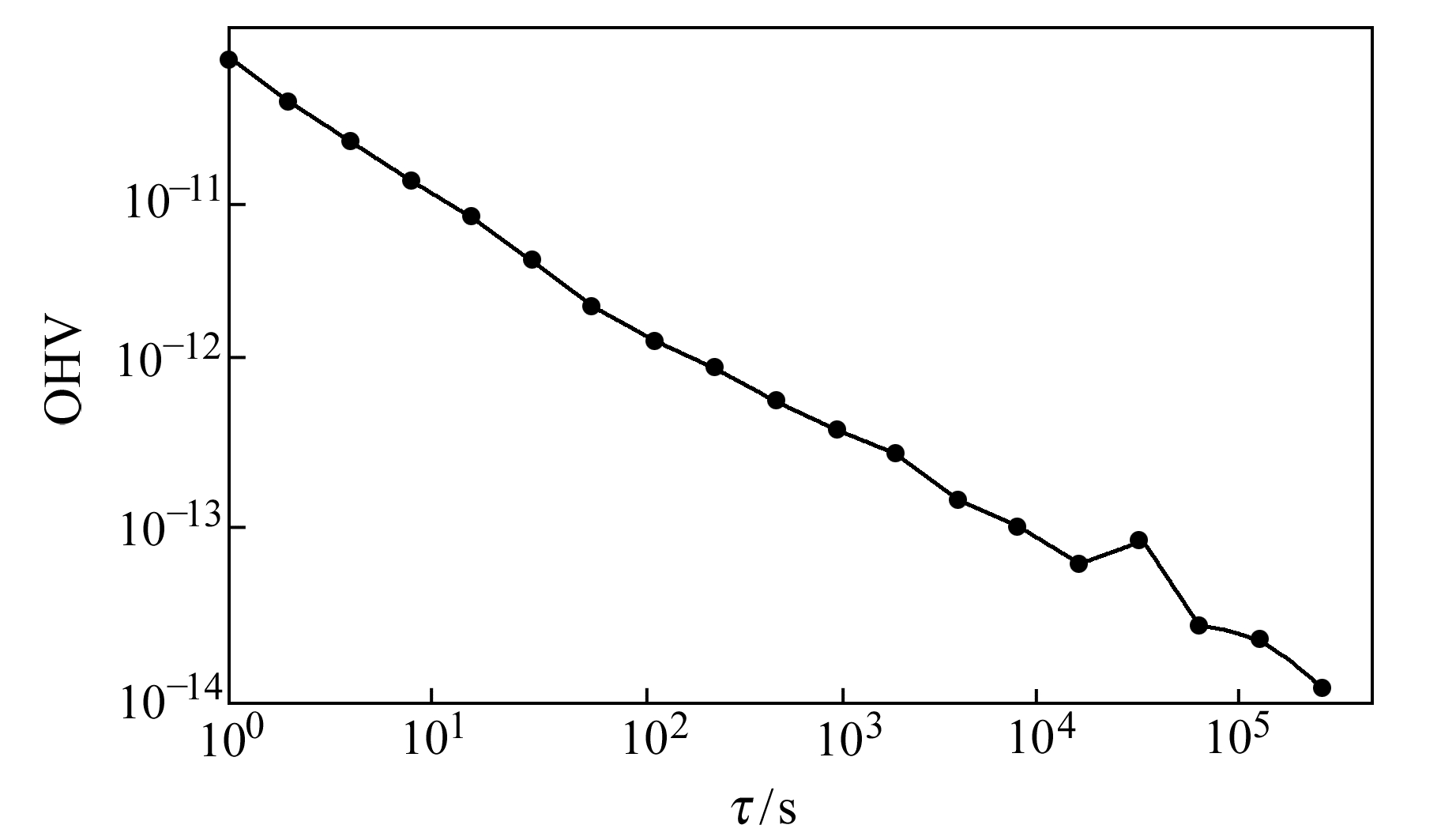
图 7 IGSO-3 OHV数据(10月) Fig. 7 OHV of IGSO-3(October) |
|
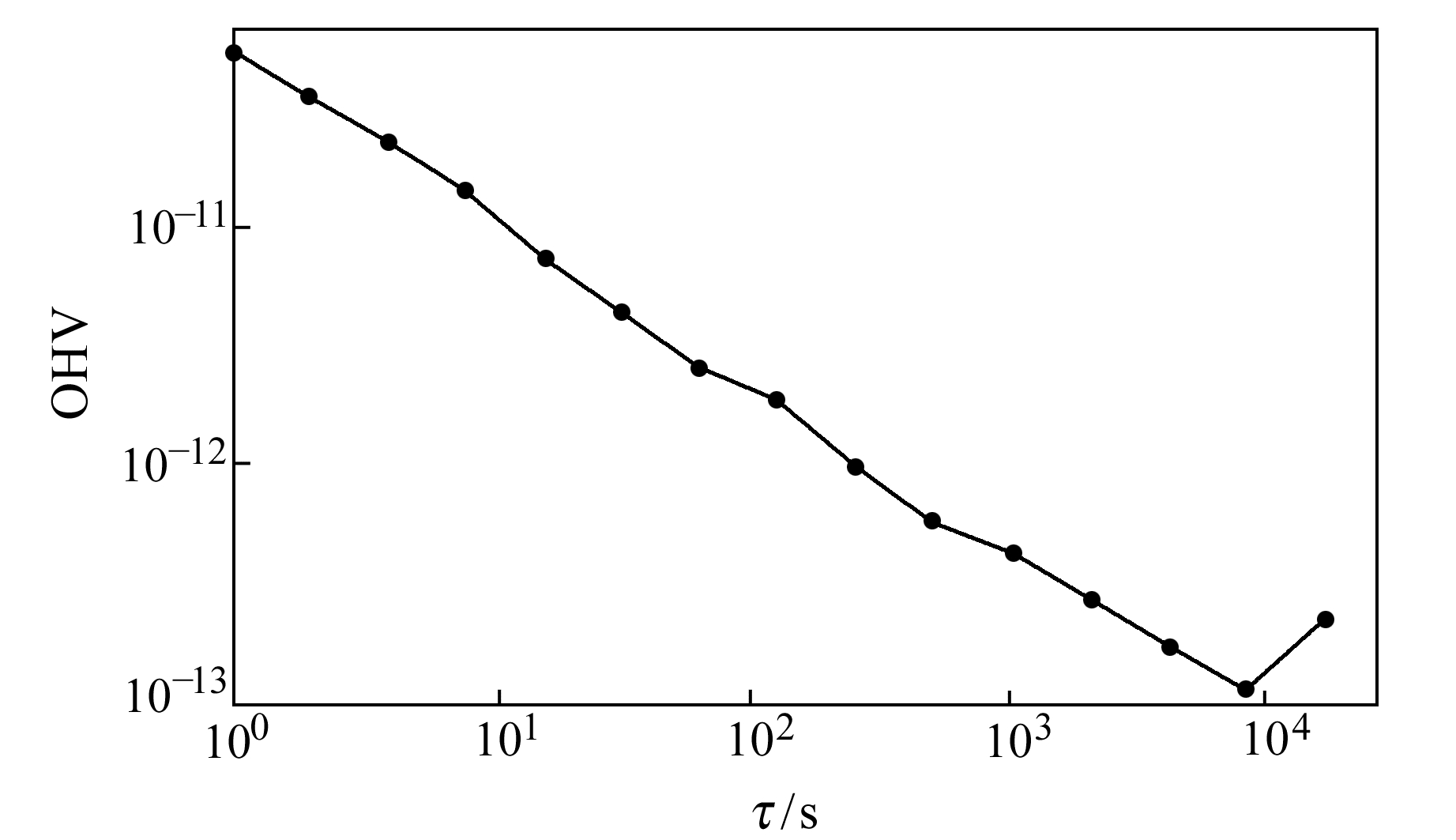
图 8 MEO-4 OHV数据(10月) Fig. 8 OHV of MEO-4(October) |
从图 1~4(T=0对应UTC 2006-01-01 00:00:00,即北斗时的起点)可以看出,GEO-1卫星钟8~9月份和IGSO-3卫星钟10月份钟差的变化量在125 μs以内,MEO-4卫星钟10月份的变化量在10 μs以内,均呈现整体平稳的变化趋势。依据数据整体情况,结合不少于15 d的评估天数要求,选取各时间段的所有数据进行处理分析。
为方便表述,下文用OHV表示重叠Hadamard方差。
从图 5~8可以看出,GEO-1卫星和IGSO-3卫星原子钟评估时段内OHV天稳值为10-14量级,优于指标设计要求;MEO-4卫星原子钟评估时段内OHV万秒稳值为1.30×10-13,优于指标设计要求。GEO-1卫星在平滑时间τ>104 s后变化较平缓,OHV万秒稳值与天稳值相差较小,IGSO-3卫星相差相对较大,并且IGSO-3卫星和MEO-4卫星在τ>104 s后起伏较大。
2.2 评估结果对比分析及结论北斗二号卫星导航系统在轨卫星原子钟的设计寿命为8 a[6],截至2017-12,GEO-1卫星、IGSO-3卫星和MEO-4卫星的在轨运行时间分别为7年11个月、6年6个月和5年7个月。其中GEO-1卫星即将到使用寿命,其余2颗卫星的在轨运行时间均已超过设计寿命的一半。但从表 1来看,这3颗卫星的星载主钟性能指标均满足设计要求,呈现正常的运行状态,仍可保证北斗系统稳定运行。为方便表示,GEO-1卫星9月份记为GEO-1(9),其他类似,各项性能指标的优劣情况如下:1)频率准确度平均值为3.71×10-11,其中MEO-4(10)评估值-8.71×10-13最优,GEO-1(9)评估值4.67×10-11最差;2)频率漂移率平均值为2.45×10-14/d,其中GEO-1(8)评估值1.61×10-15 /d最优,MEO-4(10)评估值6.27×10-14 /d最差;3)OHV万秒稳定度平均值为7.96×10-14,其中GEO-1(9)评估值5.65×10-14最优,MEO-4(10)评估值1.38×10-13最差;4)OHV天稳定度平均值为5.74×10-14,其中IGSO-3(10)评估值2.45×10-14最优,GEO-1(7)评估值1.11×10-13最差。
|
|
表 1 评估结果汇总 Tab. 1 Summary of evaluation results |
可以看出,MEO-4卫星频率漂移率和稳定度的评估结果较差,GEO-1(7)稳定度评估结果与其他月份相比结果较差,而频率准确度和漂移率基本相同。由此推断,GEO-1卫星在7月份在轨运行期间可能受到空间环境的影响[7-8],导致其频率稳定度变差。但从整体来看,虽然这3颗卫星的原子钟性能指标评估结果略有差异,但基本都在同一量级,说明卫星钟运行状况正常,无明显故障现象。
3 结语北斗二号系统自2010年发射第一颗卫星起截至2017-12,已有15颗BD-2卫星在轨运行并提供服务[6]。本文选取3颗较具代表性的BD-2在轨卫星——在轨运行时间最长且即将到设计寿命的GEO-1卫星、非静止轨道的IGSO-3卫星和MEO-4卫星的原子钟作为评估对象,基于星地无线电双向卫星钟差数据计算其选定时段的频率准确度、稳定度和漂移率,通过对计算结果的对比分析,得到以下结论:
1) 频率准确度平均值为3.71×10-11,频率漂移率平均值为2.45×10-14/d,万秒稳定度平均值为7.96×10-14,天稳定度平均值为5.74×10-14;
2) 3颗卫星的原子钟运行正常,各项性能指标均符合设计要求,未出现因老化而导致性能不达标的情况;
3) GEO-1卫星性能指标的评估结果较IGSO-3和MEO-4没有明显变差,存在超期服役的可能。
本文的评估结果在一定程度上说明,BD-2在轨卫星原子钟在其有效寿命期内运行状况正常,未出现影响系统服务的情况,可为北斗二号系统的精稳运行提供保障,同时也为正处于全面建设的北斗全球卫星导航系统(北斗三号系统)的建设和维护提供相关参考和借鉴。由于本文选取的卫星数和时段长度不是特别充足,且分析过程主要侧重数据特性,对造成劣数据的影响因素和解决措施未进行深入探索,今后将在此方面进行更加深入的探索研究。
| [1] |
郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州: 信息工程大学, 2006 (Guo Hairong.Study on the Analysis Theories and Algorithms of Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D].Zhengzhou: Information Engineering University, 2006) http://cdmd.cnki.com.cn/Article/CDMD-90008-2007051629.htm
(  0) 0) |
| [2] |
贾小林, 冯来平, 毛悦, 等. GPS星载原子钟性能评估[J]. 时间频率学报, 2010, 33(2): 115-120 (Jia Xiaolin, Feng Laiping, Mao Yue, et al. Performance Evaluation of GPS On-Board Clock[J]. Journal of Time and Frequency, 2010, 33(2): 115-120 DOI:10.3969/j.issn.1674-0637.2010.02.006)
(  0) 0) |
| [3] |
孙大双, 王宇谱, 万琪, 等. 北斗在轨卫星钟产品质量分析[J]. 测绘科学技术学报, 2017, 34(3): 251-257 (Sun Dashuang, Wang Yupu, Wan Qi, et al. On-Orbit Beidou Satellite Clock Products Quality Analysis[J]. Journal of Geomatics Science and Technology, 2017, 34(3): 251-257)
(  0) 0) |
| [4] |
毛悦, 陈建鹏, 戴伟, 等. 星载原子钟稳定性影响分析[J]. 武汉大学学报:信息科学版, 2011, 36(10): 1182-1186 (Mao Yue, Chen Jianpeng, Dai Wei, et al. Analysis of On-Board Atomic Clock Stability Influences[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1182-1186)
(  0) 0) |
| [5] |
北斗卫星导航系统: 系统介绍-发射记录[EB/OL].http://www.beidou.gov.cn/xtjs.html, 2017 (Beidou Navigation Satellite System: System Introduction-Launch Record[EB/OL].http://www.beidou.gov.cn/xtjs.html, 2017)
(  0) 0) |
| [6] |
宋杰. 中国北斗系统将正式开始全球组网"北斗+互联网+其他行业"构建新兴产业链[J]. 中国经济周刊, 2017(23): 76-77 (Song Jie. BDS Formally Start Global Networking and Build a New Industrial Chain by "BDS, Internet and Other Industries"[J]. China Economic Weekly, 2017(23): 76-77)
(  0) 0) |
| [7] |
高为广, 蔺玉亭, 陈谷仓, 等. 北斗系统在轨卫星钟性能评估方法及结论[J]. 测绘科学技术学报, 2014, 31(4): 342-346 (Gao Weiguang, Lin Yuting, Chen Gucang, et al. The Performances Assessment Methods and Results of In-Orbit Atomic Clocks of BDS[J]. Journal of Geomatics Science and Technology, 2014, 31(4): 342-346 DOI:10.3969/j.issn.1673-6338.2014.04.003)
(  0) 0) |
| [8] |
太阳活动预报中心.历史数据[EB/OL].http://rwcc.bao.ac.cn/history/sunActivity.jsp, 2017 (Regional Warning Center of China. Historical Data[EB/OL].http://rwcc.bao.ac.cn/history/sunActivity.jsp, 2017)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

