2. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
BDS三频载波相位组合观测值的优化选取是北斗系统优势发挥的关键[1]。传统意义上,在三频载波相位组合观测值的筛选过程中,首先要根据长波长、弱电离层和弱观测噪声的标准搜索并输出一系列组合,然后再结合原始观测数据,逐一进行人工筛选与分析[2]。当组合方式较多时,传统方法效率低,即使花费较大工作量,也难以筛选出满足适用条件的最优组合观测值。针对传统三频组合观测值筛选方式的不足,本文引入三频组合观测量的定义,对其进行误差分析,并基于模糊C均值聚类(FCM)算法对BDS三频组合观测值进行分类优化选取,最后利用矩阵变换法,并结合实测数据对聚类结果进行分析验证。
1 BDS载波相位观测值筛选站、星间求双差可以消除卫星和接收机的钟差及设备延迟误差。略去接收机与卫星标记以及双差符号,双差载波相位观测方程可简化为:
| $ {\varphi _i} = {\lambda _i}{\varphi _i} = \rho - {\mu _i}I + {\varepsilon _i} + {\lambda _i}{N_i}f $ | (1) |
式中,i=1、2、3,代表不同频率;λi对应不同频率的波长;Ni为模糊度;μi=(f1/fi)2;εi为以m为单位的观测噪声误差。
对三频观测值进行线性组合,得到:
| $ \begin{array}{l} {\varphi _{\rm{c}}} = \alpha {\varphi _{\rm{1}}} + \beta {\varphi _{\rm{2}}} + \gamma {\varphi _{\rm{3}}} = \\ \left( {\alpha + \beta + \gamma } \right)\rho - {\mu _{\rm{c}}}I + {\varepsilon _{\rm{c}}} + {\lambda _{\rm{c}}}{N_{\rm{c}}} \end{array} $ | (2) |
式中,φc代表三频载波相位组合观测值,其中α、β、γ为其组合观测系数;μc和λcNc的计算公式:
| $ \left\{ \begin{array}{l} {\mu _{\rm{c}}} = \alpha + \beta {\mu _2} + \gamma {\mu _3}\\ {\lambda _{\rm{c}}}{N_{\rm{c}}} = \alpha {\lambda _{\rm{1}}}{N_1} + \beta {\lambda _{\rm{2}}}{N_2} + \gamma {\lambda _{\rm{3}}}{N_3} \end{array} \right. $ | (3) |
由式(3)可得:
| $ {N_{\rm{c}}} = \alpha {\lambda _{\rm{1}}}{N_1} + \left( {\gamma {\lambda _{\rm{3}}}/{\lambda _{\rm{c}}}} \right){N_2} + \left( {\gamma {\lambda _{\rm{3}}}/{\lambda _{\rm{c}}}} \right){N_3} $ | (4) |
为保证组合观测量中卫星到接收机的几何距离不随组合系数的不同而改变,可令
| $ \alpha + \beta + \gamma = 1 $ | (5) |
式(4)中,令
| $ j = \alpha {\lambda _1}/{\lambda _{\rm{c}}}, k = \beta {\lambda _2}/{\lambda _{\rm{c}}}, l = \gamma {\lambda _3}/{\lambda _{\rm{c}}} $ | (6) |
为保证组合模糊度依旧具有整数特性,要求j、k、l均为整数,则有:
| $ {N_c} = j{N_1} + k{N_2} + l{N_3} $ | (7) |
式(6)可变换为:
| $ \alpha = j{\lambda _{\rm{c}}}/{\lambda _{\rm{1}}}, \beta = k{\lambda _{\rm{c}}}/{\lambda _{\rm{2}}}, \gamma = l{\lambda _{\rm{c}}}/{\lambda _{\rm{3}}} $ |
结合式(5)可得组合波长和组合频率分别为:
| $ {\lambda _{\rm{c}}} = \frac{{{\lambda _1}{\lambda _2}{\lambda _3}}}{{j{\lambda _2}{\lambda _3} + k{\lambda _1}{\lambda _3} + l{\lambda _1}{\lambda _2}}} $ | (8) |
| $ {f_{\rm{c}}} = \frac{c}{{{\lambda _{\rm{c}}}}} = j{f_1} + k{f_2} + l{f_3} $ | (9) |
理论上三频观测量可以形成无穷组的组合,但具有实际应用价值的组合需要满足以下标准:
1) 波长标准。
在三频组合观测值整周模糊度的固定过程中,组合波长的大小起到重要作用。当组合观测量波长较长时,可以有效削弱多路径效应和观测噪声,并减轻其对周跳探测与修复以及模糊度解算的影响,提高解算精度。
2) 电离层延迟标准。
长距离相对定位时,卫星信号穿过电离层会因各种因素干扰而产生延迟误差,影响整周模糊度的解算,伪距和载波相位观测量的电离层延迟大小相同、符号相反。组合观测量优化选取需有较小的电离层延迟误差放大系数。
以周为单位的电离层延迟误差放大系数为:
| $ \overline {{\mu _{\rm{c}}}} = \frac{1}{{{\lambda _1}}}\left( {j{\lambda _1} + k{\lambda _2} + l{\lambda _3}} \right) $ |
3) 观测噪声标准。
BDS的观测噪声受信噪比影响,伪距观测噪声一般为码元长度的1%左右,载波相位观测噪声一般在0.001~0.1周之间变化,优选组合观测量需有较小的观测噪声放大系数。
假设BDS的三个频点上的载波观测噪声具有相同的标准差,即σε1=σε2=σε3=σε,则以周为单位的组合观测噪声标准差σεc可以表示为:
本文任意选取部分线性组合,其相关的特性指标见表 1。
|
|
表 1 BDS三频载波相位组合观测值 Tab. 1 Triple-frequency carrier phase combinations |
在FCM算法中,首先随机设定C个初始聚类中心,然后根据某种相似度计算方法,计算数据集中的其他数据对象与C个初始聚类中心的距离函数以及隶属度关系。反复循环迭代,直到聚类中心不再产生变化,得到最优划分结果,最终实现将N个L维向量分为C个模糊组。其中,目标函数为:
| $ J\left( {U, V} \right) = \sum\limits_{i = 1}^N {\sum\limits_{{\rm{c}} = 1}^C {u_{ic}^m{d^2}\left( {{x_i}, {v_{\rm{c}}}} \right)} } $ | (10) |
式中,m指模糊加权系数,其值大于1;d(xi, vc)表示第i个数据点与第c个聚类中心的欧氏距离;uic是隶属度矩阵中的元素,且∈[0, 1];vc对应每个簇集的聚类中心。
约束条件:
根据隶属度的非负性,有uic≥0 ∀i, c并且
为求目标函数(含有约束条件)的极值,在此引入拉格朗日因子,可构造新的目标函数:
| $ \begin{array}{*{20}{c}} {{J_\lambda }\left( {U, V} \right) = \sum\limits_{i = 1}^N {\sum\limits_{c = 1}^C {u_{ic}^m{d^2}\left( {{x_i}, {v_{\rm{c}}}} \right)} } + }\\ {\lambda \left( {\sum\limits_{c = 1}^C {{u_{ic}}} - 1} \right)} \end{array} $ | (11) |
目标函数求极值的最优化条件如下:
| $ \left\{ \begin{array}{l} \frac{{\partial {J_\lambda }}}{{\partial \lambda }} = \left( {\sum\limits_{i = 1}^N {\sum\limits_{c = 1}^C {{u_{ic}}} } - 1} \right) = 0\\ \frac{{\partial {J_\lambda }}}{{\partial {u_{ic}}}} = \left( {\sum\limits_{i = 1}^N {\sum\limits_{c = 1}^C {m{{\left( {{u_{ic}}} \right)}^{m - 1}}{d^2}\left( {{x_i}, {v_c}} \right)} } - \lambda } \right) = 0\\ \frac{{\partial {J_\lambda }}}{{\partial {v_c}}} = \left( {\sum\limits_{i = 1}^N {\sum\limits_{c = 1}^C {{{\left( {{u_{ic}}} \right)}^m}{x_i}} } - {v_c}\sum\limits_{i = 1}^n {u_{ic}^m} } \right) = 0 \end{array} \right. $ | (12) |
综上可得隶属度以及聚类中心的计算公式:
| $ {u_{ic}} = \frac{1}{{\sum\limits_{c = 1}^C {{{\left( {\frac{{d\left( {{x_i}, {v_c}} \right)}}{{d\left( {{x_t}, {v_c}} \right)}}} \right)}^{m - 1}}} }}, {v_c} = \frac{{\sum\limits_{i = 1}^N {u_{ic}^m{x_i}} }}{{\sum\limits_{i = 1}^N {u_{ic}^m} }} $ | (13) |
将式(13)进行循环迭代,可以求得满足约束条件的隶属度和聚类中心。
2.2 算法流程经过§2.1分析,最优观测量组合的选取指标可用以下3个量来表示:波长λ、电离层延迟误差放大系数
FCM算法流程(图 1)如下:

|
图 1 FCM算法流程 Fig. 1 Flow char of FCM algorithm |
1) 给定数据集Y,其由N个L维向量组成,设置聚类数C(2≤C≤N),并自定义隶属度矩阵。由表 1可知N=14,L=3,取C=4。设定模糊系数m(一般取2),迭代停止阈值ε(一般取0.001~0.01),迭代次数l,初始化聚类原型v(l)(l=0)[5-6]。
2) 初始化隶属度矩阵且满足式(12)归一化条件。
3) 根据式(13)计算聚类中心和隶属度矩阵。
4) 根据矩阵范数比较迭代的隶属度矩阵,直到所得聚类中心以及聚类结果收敛到不再变化。
3 结果分析与算法验证 3.1 结果分析基于长波长、弱电离层延迟和低观测噪声的筛选标准,运用FCM算法,对表 1中的14组BDS载波相位组合观测值进行聚类分析[7-8]。设定聚类数C=4,迭代停止阈值ε=0.001,迭代次数l=100,聚类结果如表 2和图 2所示。
|
|
表 2 模糊聚类结果 Tab. 2 Fuzzy clustering results |
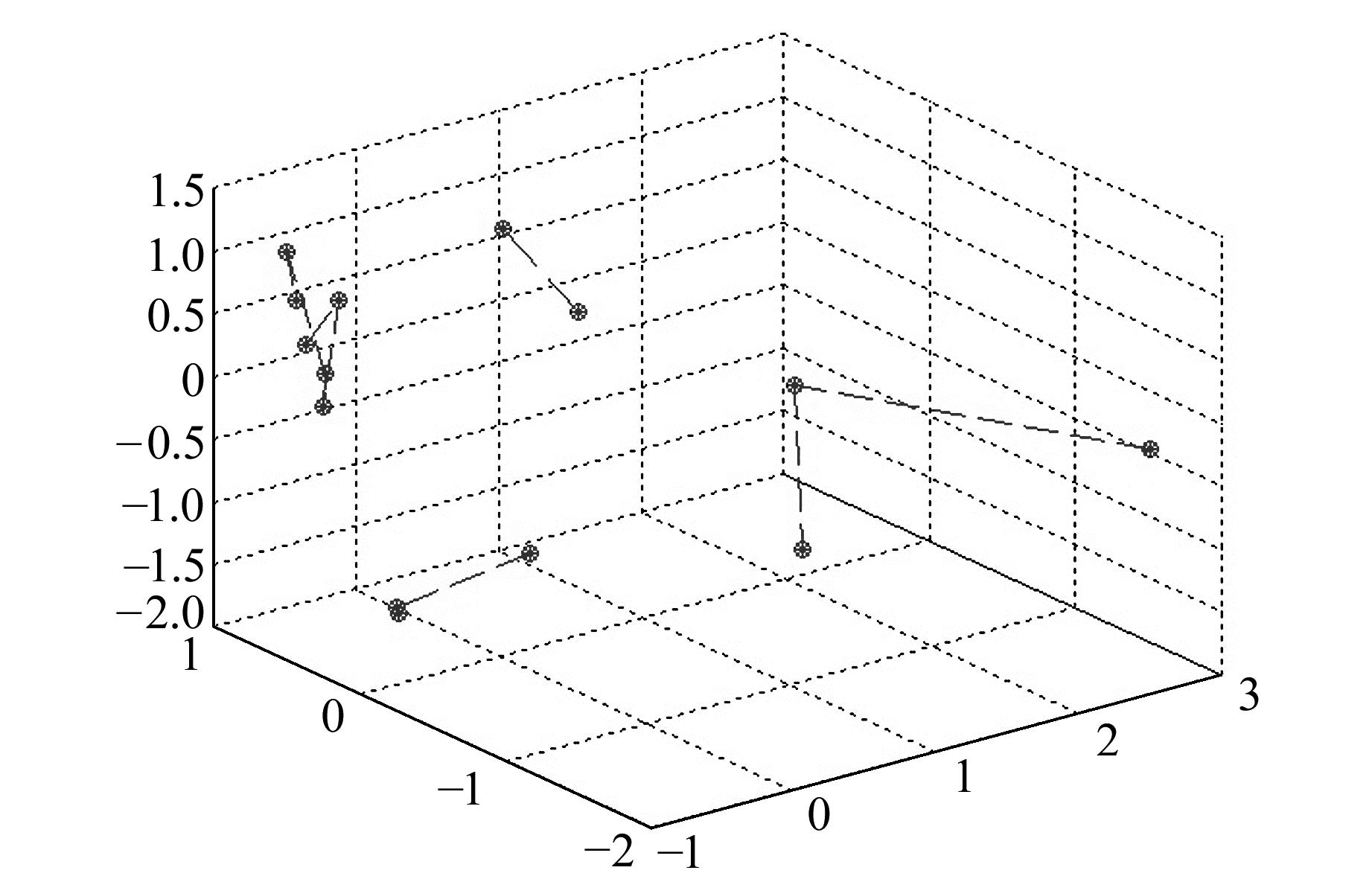
|
图 2 模糊聚类输出结果 Fig. 2 Fuzzy clustering results |
对照表 1可知,第Ⅰ类包括组合2(φ1, 4,-5)及组合5(φ-1,-6, 7),二者均具有j+k+l=0的特性,为无几何组合,其λ较长,以周为单位的
第Ⅱ类包括组合4(φ0,-1,1)、组合7(φ1,0,-1)、组合10(φ1,-1, 0),三者均为双频组合,虽然组合的λ较短,但其
第Ⅲ类包括组合1(φ4,-2,-3)、组合3(φ3,-8,4)、组合8(φ4,-3,-2),这3种组合的λ较长,但是η较大,
第Ⅳ类包括组合6(φ5,1,-5)、组合9(φ6,1,-6)、组合11(φ5,-1,-3)、组合12(φ4,-5,2)、组合13(φ5,3,-7)、组合14(φ5,2,-6),这类组合的λ更短,其中组合6、组合9、组合13、组合14的
采用矩阵变换法对实测BDS三频载波相位组合观测值进行模糊度的解算。矩阵变换求解模糊度是利用三频伪距观测值和三频载波相位观测值直接求解模糊度的一种方法,它通过类似于LAMBDA方法的Z变换将组合观测值的模糊度方差变换到精度允许的范围之内,从而提高模糊度固定的速度[9]。
对于两个观测历元和两台接收机,假定每个历元可以接收到B1、B2、B3三个频率的伪距和载波相位观测值,对流层延迟量被归在几何误差项中,此时三频双差伪距和载波相位观测值可组成6个双差观测方程:
| $ \left\{ \begin{array}{l} \nabla \Delta {P_i} = \nabla \Delta {\rho _i} + {q_i}\nabla \Delta {I_i} + \nabla \Delta {T_i} + \nabla \Delta {\varepsilon _{i, r}}\\ {\lambda _i}\nabla \Delta {\varphi _i} = \nabla \Delta {\rho _i} - {\lambda _i}\nabla \Delta {N_i} - \\ \;\;\;\;\;\;\;{q_i}\nabla \Delta {I_i} + \nabla \Delta {T_i} + \nabla \Delta {\varepsilon _{i, \varphi }} \end{array} \right. $ | (14) |
式中,i=1,2,3;
假设伪距观测方程中B1、B2、B3的观测值标准差相同(用σR表示),对于BDS导航定位测量,对几何距离
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\nabla \Delta \rho }\\ {\nabla \Delta I} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {2.566\;43}&{ - 1.228\;92}&{ - 0.337\;51}\\ { - 1.600\;05}&{1.119\;38}&{0.480\;67} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\nabla \Delta {P_1}}\\ {\nabla \Delta {P_2}}\\ {\nabla \Delta {P_3}} \end{array}} \right]} \end{array} $ | (15) |
由3个频率的双差载波观测方程解出3个频率的双差模糊度:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\nabla \Delta {N_1}}\\ {\nabla \Delta {N_2}}\\ {\nabla \Delta {N_3}} \end{array}} \right] = - \left[ {\begin{array}{*{20}{c}} {\nabla \Delta {\varphi _1}}\\ {\nabla \Delta {\varphi _2}}\\ {\nabla \Delta {\varphi _3}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {21.700\;53}&{ - 12.230\;84}&{ - 4.261\;36}\\ {21.138\;77}&{ - 12.504\;12}&{ - 4.602\;39}\\ {21.142\;86}&{ - 12.390\;82}&{ - 4.514\;75} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\nabla \Delta {P_1}}\\ {\nabla \Delta {P_2}}\\ {\nabla \Delta {P_3}} \end{array}} \right]} \end{array} $ | (16) |
假设载波观测方程中B1、B2、B3伪距和载波相位观测值标准差相同(用σφ来表示),将3个频段的波长和频率值代入,可得双差模糊度的方差-协方差矩阵:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_N} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right]\sigma _\varphi ^2 + }\\ {\left[ {\begin{array}{*{20}{c}} {638.403\;5}&{630.253\;6}&{628.585\;8}\\ {630.253\;6}&{622.627\;5}&{620.898\;8}\\ {628.585\;8}&{620.898\;8}&{619.190\;5} \end{array}} \right]\sigma _R^2} \end{array} $ | (17) |
式中,原始模糊度的方差值较大,且模糊度间的相关性较高,难以实现模糊度快速固定。为降低模糊的相关性并减小模糊度方差,应用整数变换的方法对原始模糊度进行整数变换。设变换矩阵为Z,原始模糊度矩阵为N,则有:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\bar N}} = \mathit{\boldsymbol{ZN}}\\ {{\mathit{\boldsymbol{\bar D}}}_N} = \mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{D}}_N}{\mathit{\boldsymbol{Z}}^{\rm{T}}} \end{array} \right. $ | (18) |
式中,Z为3个线性组合的系数组成的转换矩阵。为了保证转换后的模糊度N具有整数特性,转换矩阵Z及其逆阵必须具有整数特性并且其行列式值等于1。
这里选取组合2(φ1,4,-5)、组合4(φ0,-1,1)和组合13(φ5,3,-7)、组合14(φ5,2,-6)分别组成转换矩阵Z1和Z2。
| $ {\mathit{\boldsymbol{Z}}_1} = \left[ {\begin{array}{*{20}{c}} 1&4&{ - 5}\\ 0&{ - 1}&1\\ 4&2&{ - 7} \end{array}} \right], {\mathit{\boldsymbol{Z}}_2} = \left[ {\begin{array}{*{20}{c}} 5&3&{ - 7}\\ 5&2&{ - 6}\\ 4&{ - 5}&2 \end{array}} \right] $ |
令σφ=0.01周,σR=0.3 m,经矩阵变换后的模糊度方差-协方差为:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar D}}}_{{N_1}}} = \left[ {\begin{array}{*{20}{c}} {0.042\;4}&{ - 0.004\;6}&{ - 1.354\;7}\\ { - 0.004\;6}&{0.002\;0}&{0.163\;8}\\ { - 1.354\;7}&{0.163\;8}&{48.917\;7} \end{array}} \right]\\ {{\mathit{\boldsymbol{\bar D}}}_{{N_2}}} = \left[ {\begin{array}{*{20}{c}} {65.971\;3}&{65.829\;2}&{63.809\;1}\\ {65.829\;2}&{65.689\;2}&{63.679\;8}\\ {63.809\;1}&{63.679\;8}&{61.759\;7} \end{array}} \right] \end{array} $ | (19) |
由式(19)可以看出,通过Z2变换得出的标准差比通过Z1变换得出的标准差要大很多。其中,组合4(φ0,-1,1)的标准差非常小(0.044 7周),无论基线长短,都可以在短时间内采用伪距/相位法直接固定。组合2(φ1,4,-5)的标准差也较小(0.205 9周),短基线时可采用伪距/相位法直接固定。组合13(φ5,3,-7)(8.122 3周)、组合14(φ5,2,-6)(8.104 9周)的标准差都比较大,短时间内难以完成固定。因此组合2的模糊度固定效果不如组合1的好。根据实测BDS观测数据,利用B1、B2、B3三个频点的观测值,测定模糊度相邻历元间的差值如图 3~6所示。
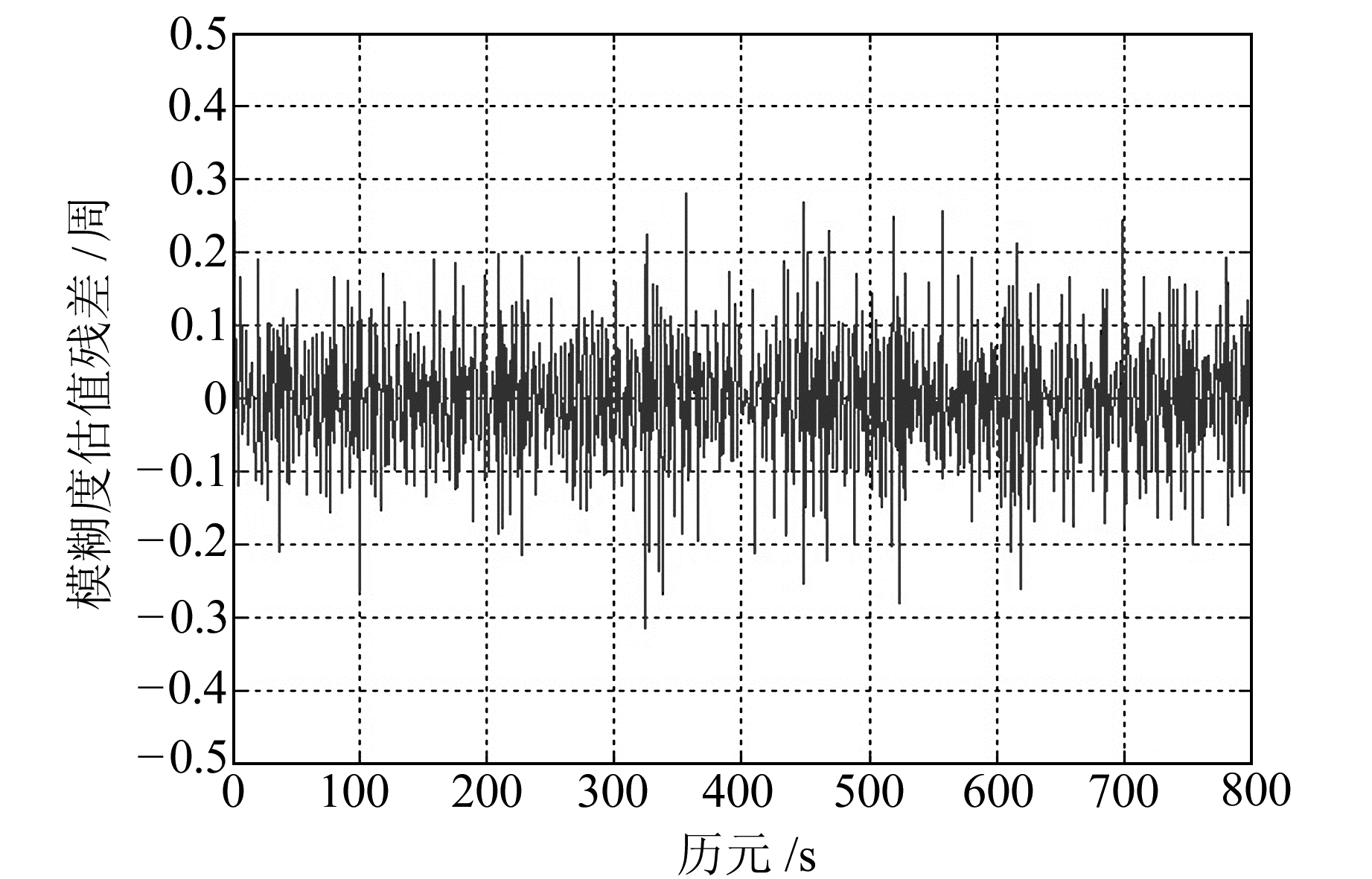
|
图 3 组合2(φ1,4,-5)历元间模糊度差值 Fig. 3 Ambiguity difference of combination 2(φ1, 4, -5) between each epoch |
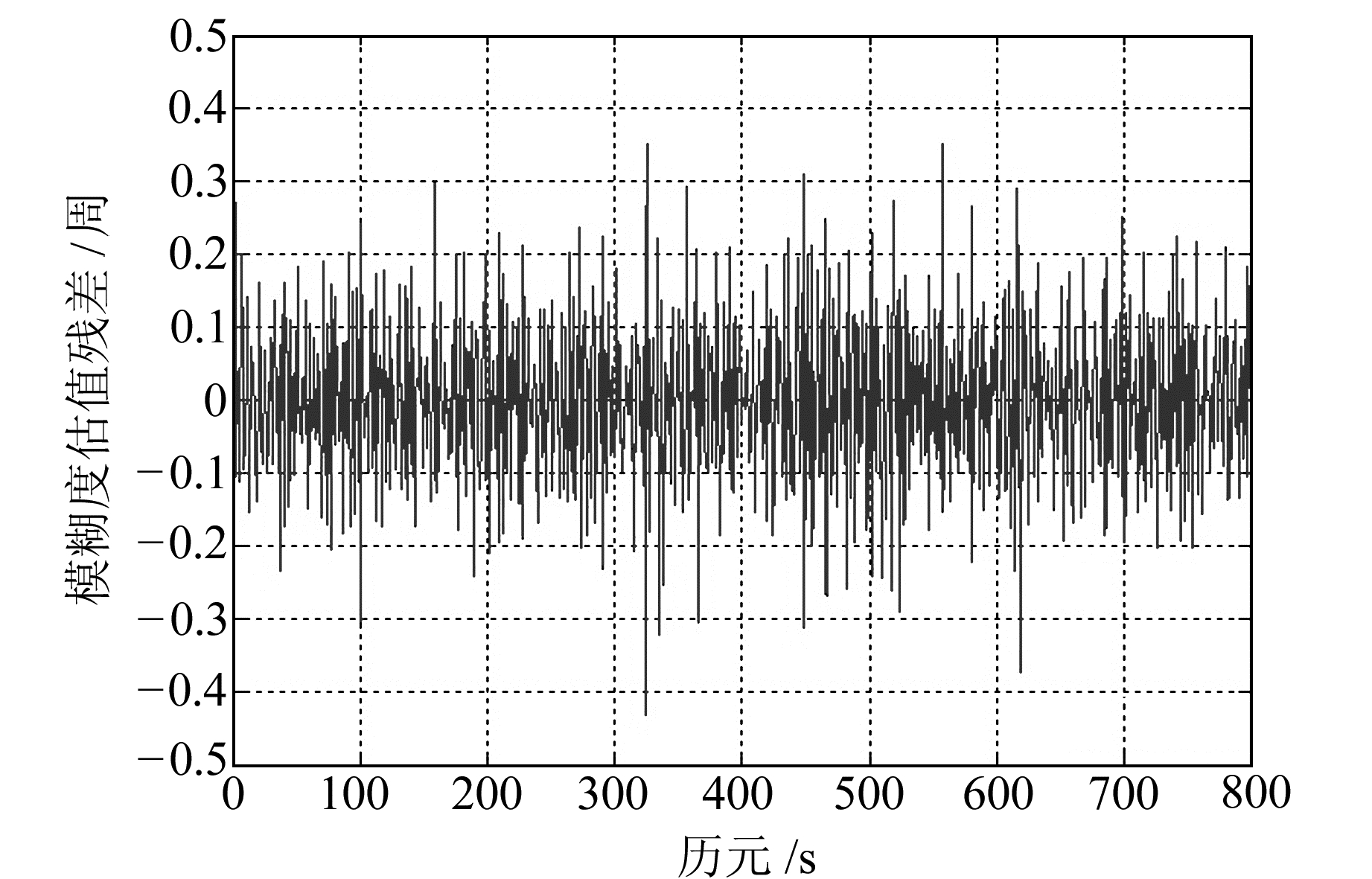
|
图 4 组合4(φ0,-1,1)历元间模糊度差值 Fig. 4 Ambiguity difference of combination 4(φ0, -1, 1) between each epoch |

|
图 5 组合13(φ5,3,-7)历元间模糊度差值 Fig. 5 Ambiguity difference of combination 13(φ5, 3, -7) between each epoch |
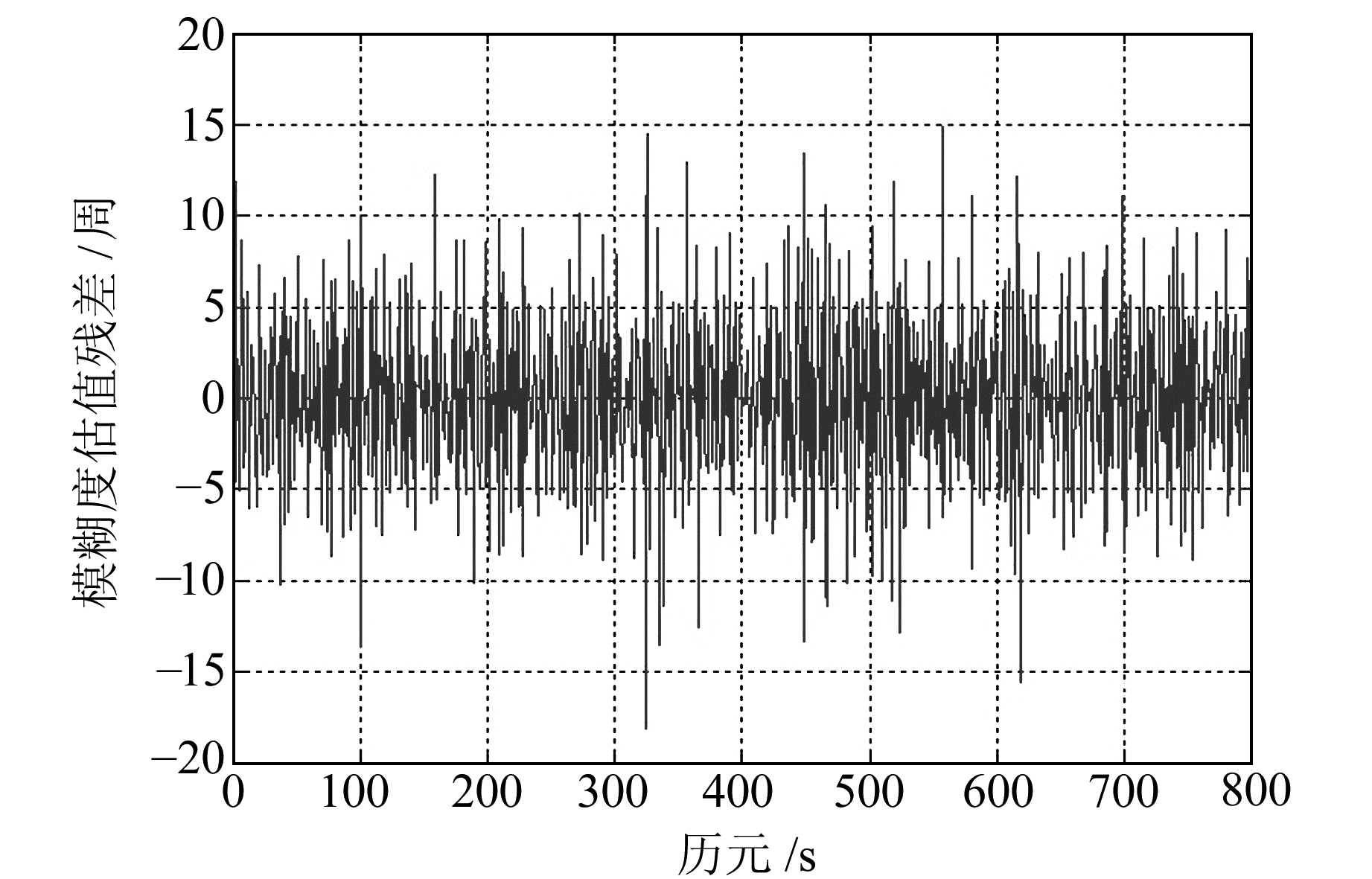
|
图 6 组合14(φ5,2,-6)历元间模糊度差值 Fig. 6 Ambiguity difference of combination 14(φ5, 2, -6) between each epoch |
由图 3和图 4可知,组合2(φ1, 4,-5)、组合4(φ0,-1,1)相邻历元组合双差模糊度差值较小,在0.5周以内。由图 5和图 6可知,组合13(φ5,3,-7)、组合14(φ5,2,-6)相邻历元组合双差模糊度差值较大,最大接近20周,短时间内难以对模糊度进行固定。由此可得,组合2(φ1,4,-5)和组合4(φ0,-1,1)的特性要比组合13(φ5,3,-7)、组合14(φ5,2,-6)好。
4 结语本文在对BDS三频组合观测值进行误差分析的基础上,依据长波长、弱电离层观测系数、弱观测噪声的标准,运用模糊C均值聚类方法对所选部分线性组合进行分类,实现了BDS三频组合观测值的自动优化选取,有效解决了传统筛选方法效率低、工作量大的问题。最后通过分析可知,利用本文方法所得到的优化组合与传统方法得到的优化组合相一致,同时利用矩阵变换法可以在较短时间里实现对模糊度的固定,进一步证明了该方法的可靠性。
| [1] |
李克昭, 孟福军, 丁安民, 等. BDS多频组合模糊度解算方法研究[J]. 河南理工大学学报:自然科学版, 2015, 34(1): 53-58 (Li Kezhao, Meng Fujun, Ding Anmin, et al. Research on Method of Integer Ambiguity Resolution Algorithm by BDS Multi-Frequency Combination[J]. Journal of Henan Polytechnic University:Natural Science, 2015, 34(1): 53-58)
(  0) 0) |
| [2] |
刘亚涛, 胡晓粉, 张冲, 等. 基于模糊C均值聚类的载波相位组合观测值优化选取[J]. 导航定位学报, 2013, 1(4): 89-92 (Liu Yatao, Hu Xiaofen, Zhang Chong, et al. Optimization of Carrier Phase Combination Observations Selection Based on Fuzzy C-Means Algorithm[J]. Journal of Navigation and Positioning, 2013, 1(4): 89-92 DOI:10.3969/j.issn.2095-4999.2013.04.020)
(  0) 0) |
| [3] |
何伟, 陶庭叶, 王志平. 基于改进FCM的北斗三频组合观测值选取[J]. 中国空间科学技术, 2014, 34(4): 24-30 (He Wei, Tao Tingye, Wang Zhiping. Selection on Improved Fuzzy C-Means Algorithm of BeidouTriple-Frequency Combination Observations[J]. Chinese Space Science and Technology, 2014, 34(4): 24-30)
(  0) 0) |
| [4] |
黄令勇, 宋力杰, 刘先冬. 基于自适应聚类算法的GPS三频载波相位组合观测值优化选取[J]. 大地测量与地球动力学, 2011, 31(4): 99-102 (Huang Lingyong, Song Lijie, Liu Xiandong. Optimization and Selection of GPS Triple-Carriers Phase Combination Observations Based Self-Adaptive Clustering[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 99-102)
(  0) 0) |
| [5] |
王勇, 赵修斌, 庞春雷, 等. BDS/GPS四频组合观测值系数选择方法与分析[J]. 空军工程大学学报:自然科学版, 2014(4): 70-74 (Wang Yong, Zhao Xiubin, Pang Chunlei, et al. A Selective Method and Analysis of BDS/GPS Four-Frequency Combination Observational Coefficients[J]. Journal of Air Force Engineering University:Natural Science Edition, 2014(4): 70-74)
(  0) 0) |
| [6] |
邢喆, 王泽民, 伍岳. 利用模糊聚类方法筛选GPS载波相位组合观测值[J]. 武汉大学学报:信息科学版, 2006, 31(1): 23-26 (Xing Zhe, Wang Zemin, Wu Yue. Choice of Carrier Phase Combined Observation of GPS Using Fuzzy Cluster[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 23-26)
(  0) 0) |
| [7] |
黄令勇, 宁德阳, 吕志平, 等. 两种长基线模糊度解算方法在北斗三频应用中的比较[J]. 大地测量与地球动力学, 2014, 34(5): 101-105 (Huang Lingyong, Ning Deyang, Lü Zhiping, et al. Comparative Study on Two Long-Base Line Ambiguity Resolution Methods in Application of Beidou/Compass Triple-Frequncey[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 101-105)
(  0) 0) |
| [8] |
Feng Y M. A Completed Geometry-Free Approach to Three Carrier Ambiguity Resolutions[C]. The 2004 International Symposium on GNSS/GPS, Sydney, 2004
(  0) 0) |
| [9] |
Tang W, Deng C, Shi C, et al. Triple-Frequency Carrier Ambiguity Resolution for Beidou Navigation Satellite System[J]. GPS Solutions, 2014, 18(3): 335-344 DOI:10.1007/s10291-013-0333-9
(  0) 0) |
2. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2019, Vol. 39
2019, Vol. 39

