2. 武汉地震工程研究院有限公司,武汉市洪山侧路40号,430071;
3. 重庆交通大学河海学院,重庆市学府大道69号,400074
我国1/3的国土为山地,大量的公路、铁路、城镇和矿区建在高陡边坡附近。为了保证重要建、构筑物及设施不受到边坡失稳的威胁,必须先对边坡的稳定状态进行识别和评价。边坡的稳定性分析是边坡监测、预警和防治的首要环节,也是影响工程选址的重要因素。可靠度分析作为研究边坡稳定性的方法之一得到较为广泛的应用。彭兴等[1]提出基于蒙特卡洛模拟的岩质边坡可靠度设计方法和实用框架;蒋水华等[2]提出基于随机响应面法的边坡系统可靠度分析方法;唐小松等[3]基于Bootstrap抽样技术提出有限数据条件下边坡可靠度的分析方法。
爆破是岩质边坡开挖和石块清除的主要方法之一。爆破作业产生的强烈振动会劣化边坡的稳定性,甚至导致边坡失稳破坏。近年来,爆破对边坡稳定性的影响也成为研究热点。李维光等[4]在极限平衡理论基础上,推导出顺层岩质边坡稳定性安全系数的计算方法;王智德等[5]通过对现场监测数据的分析,获得不同药量下单次和多次爆破的顺层岩质边坡坡体损伤范围以及振动速度的衰减规律;崔铁军等[6]通过数值模拟总结了爆破高度对稳定性的影响;张飞等[7]、钟冬望等[8]、张继春等[9]分别通过数值模拟、室内和现场试验等手段探讨了爆破振动在岩质边坡中的传播规律。
在岩质边坡稳定可靠度研究方面,目前主要集中在仅考虑边坡自重和裂隙水压力等常规荷载作用下的边坡可靠度指标和失稳概率分析,而在爆破荷载作用下边坡失稳概率和可靠指标计算方法方面的研究鲜见报道。因此,基于可靠度理论建立爆破荷载作用下顺层岩质边坡的稳定性分析方法,可为爆破施工影响区域边坡的监测、预警、防治,以及边坡爆破开挖的设计、施工提供理论依据和有意义的参考。
1 可靠度求解方法计算可靠度的方法很多,但是使用最广泛的是一次二阶矩计算方法,该方法包含中心点法和验算点法。由于中心点法存在在平均值处展开不合理、未考虑随机变量的概率分布等明显缺点[10-11],所以采用验算点法计算爆破作用下顺层岩质边坡稳定的可靠度。
假设边坡稳定计算含有n个相互独立的随机变量X1,X2,…,Xn,它们的均值分别为μX1,μX2,…,μXn,标准差分别为σX1,σX2,…,σXn。由文献[11],边坡稳定性计算的功能函数可表达为:
| $ Z = {g_X}\left( {{X_1}, {X_2}, \cdots , {X_n}} \right) = {a_0} + \sum\limits_{i = 1}^n {{a_i}{X_i}} $ | (1) |
式中,ai(i=0,1,…,n)为常数。
边坡稳定计算功能函数的平均值、标准差、可靠指标和失稳概率分别为:
| $ {\mu _Z} = {a_0} + \sum\limits_{i = 1}^n {{a_i}{\mu _{{X_i}}}} $ | (2) |
| $ {\sigma _Z} = \sqrt {\sum\limits_{i = 1}^n {a_i^2\sigma _{{X_i}}^2} } $ | (3) |
| $ \beta = \frac{{{\mu _Z}}}{{{\sigma _Z}}} = \left( {{a_0} + \sum\limits_{i = 1}^n {{a_i}{\mu _{{X_i}}}} } \right)/\sqrt {\sum\limits_{i = 1}^n {a_i^2\sigma _{{X_i}}^2} } $ | (4) |
| $ {P_f} = \mathit{\Phi }\left( { - \beta } \right) $ | (5) |
式中,Φ(x)为标准正态分布函数。若边坡稳定计算中随机变量是非正态的,可用Rackwitz-Fiessler方法先对其正态化,再进行可靠度计算。
2 爆破惯性力物体质点的振动速度与爆破采用的炸药量及质心到爆破点的距离有关。根据文献[12],不稳定岩体质心处振动的峰值速度和峰值加速度分别为:
| $ {V_{\max }} = K{\left( {{Q^{1/3}}/R} \right)^\lambda } $ | (6) |
| $ {a_{\max }} = 2{\rm{ \mathit{ π} }}f{V_{\max }} $ | (7) |
式中,Vmax为不稳定岩体质心处的峰值振动速度(cm/s);Q为单次爆破的炸药量(kg);R为质心到爆破点的距离,简称爆心距(m);amax为不稳定岩体质心处由爆破引起的峰值加速度(cm/s2);K和λ为与场地条件、岩性特性、爆破条件及爆破区与观测点相对位置等有关的常数,可参考表 1取值[12]。
|
|
表 1 K和λ的参数取值表 Tab. 1 Parameter values for K and λ |
为了较好地反映爆破对不稳定岩体的影响,考虑爆破的时效性,假定爆破的加速度随峰值加速度呈周期性变化,则:
| $ a\left( t \right) = {a_{\max }}\sin \left( {\omega t + \theta } \right) $ | (8) |
| $ \omega = 2{\rm{ \mathit{ π} }}f $ | (9) |
式中,ω为角频率;θ为初相位角;f为频率。
由于爆破产生的加速度会随时间的增加而减小,通过引入衰减指数来考虑这种衰减关系,则式(8)变为:
| $ a\left( t \right) = {a_{\max }}{{\rm{e}}^{ - \psi t}}\sin \left( {\omega t + \theta } \right) $ | (10) |
式中,ψ为关于时间的衰减指数。因此,由爆破产生的作用在不稳定岩体的惯性力为:
| $ E\left( t \right) = ma\left( t \right) $ | (11) |
式中,m为不稳定岩体的质量。
设爆破惯性力与水平面的夹角为α,则水平方向和竖直方向的爆破惯性力分别为:
| $ {E_X}\left( t \right) = ma\left( t \right)\cos \alpha $ | (12) |
| $ {E_Z}\left( t \right) = ma\left( t \right)\sin \alpha $ | (13) |
图 1为顺层岩质边坡稳定可靠度的计算模型,图 1所示顺层岩质边坡的作用有滑体自重、爆破荷载、顶部的附加荷载和裂隙水压力,顺层岩质边坡的稳定系数计算式为:
| $ {F_{\rm{S}}} = {A_1}\tan \varphi + {A_2}c $ | (14) |
| $ {A_1} = {A_3}/{A_4} $ | (15) |
| $ {A_2} = L/{A_4} $ | (16) |
| $ {A_3} = \left[ {G + {E_Z}\left( t \right)} \right]\cos \theta - {E_X}\left( t \right)\sin \theta - {P_{\rm{W}}} $ | (17) |
| $ {A_4} = \left[ {G + {E_Z}\left( t \right)} \right]\sin \theta + {E_X}\left( t \right)\cos \theta $ | (18) |

|
图 1 稳定性分析模型 Fig. 1 Stability analysis model |
式中,A1、A2、A3、A4为系数,φ为滑面内摩擦角,c为滑面粘聚力,G为滑体自重,L为滑面长度,PW为裂隙水压力。
根据式(14)计算得到边坡稳定系数,当FS>1时,边坡稳定;当FS=1时,边坡处于极限平衡状态;当FS < 1时,边坡处于失稳状态。建立顺层岩质边坡可靠度计算的功能函数:
| $ Z = {F_{\rm{S}}} - 1 = {A_1}\tan \varphi + {A_2}c - 1 $ | (19) |
功能函数Z中只有tanφ和c两个随机变量,其他值都可以视为常数。设X1=tanφ,X2=c,则:
| $ Z = {\rm{g}}\left( {{X_1}, {X_2}} \right) = {A_1}{X_1} + {A_2}{X_2} - 1 $ | (20) |
根据式(20)和式(4),可得顺层岩质边坡的可靠指标为:
| $ \beta = \frac{{ - 1 + {A_1}{\mu _{{X_1}}} + {A_2}{\mu _{{X_2}}}}}{{\sqrt {A_1^2\sigma _{{X_1}}^2 + A_2^2\sigma _{{X_2}}^2} }} $ | (21) |
将式(21)计算的可靠指标代入式(5)中,即可得到顺层岩质边坡的失稳概率。文献[13]把边坡稳定性分为稳定(Pf < 5%)、基本稳定(Pf=5%~30%)、欠稳定(Pf=30%~60%)、稳定性差(Pf=60%~90%)和不稳定(Pf>90%)5个等级。将边坡失稳概率计算结果与上述稳定性划分标准相比较,就可以判定边坡的稳定状态。
4 算例分析 4.1 失稳概率计算以重庆万州某小区高切坡为例进行计算分析(图 2)。该边坡高度12.5 m,滑塌体顶部宽度8.6 m。坡顶有块体积约160 m3的不稳定巨石,为保证边坡和坡脚下建筑物的安全需将其爆破清除。坡体为单斜构造,岩层产状为125°∠32°。边坡主要岩性为泥岩,紫红色,泥质结构,薄-厚层状构造,主要由粘土矿物组成,局部砂质含量稍重,偶见灰绿色砂质团斑和条带。边坡滑动面的粘聚力和内摩擦角均服从正态分布:c~N(38 kPa,6 kPa),φ~N(29°,3°),滑体容重为24.6 kN/m3。

|
图 2 地质剖面图 Fig. 2 Geological section of high-cutting slope |
爆破设计平均单孔药量为34.8 kg,常数K和λ参考表 1分别取182和1.66。计算得到不考虑爆破和裂隙水作用时稳定系数为1.85,仅考虑爆破荷载时稳定系数为1.72,仅考虑裂隙水时稳定系数为1.17,同时考虑裂隙水和爆破荷载作用时稳定系数为1.08。计算结果表明,裂隙水压力比爆破荷载对该边坡的稳定性影响更大。
根据建立的边坡稳定可靠度计算方法得到:不考虑爆破和裂隙水作用时,边坡失稳概率为0.5%;仅考虑爆破荷载时,边坡失稳概率为2.04%;仅考虑裂隙水时,边坡失稳概率为20.54%(边坡处于基本稳定状态);同时考虑爆破和裂隙水作用时,边坡失稳概率为32.62%(边坡处于欠稳定状态)。上述结果与稳定系数计算结果一致,说明本文提出的边坡稳定可靠性分析方法是合理的。
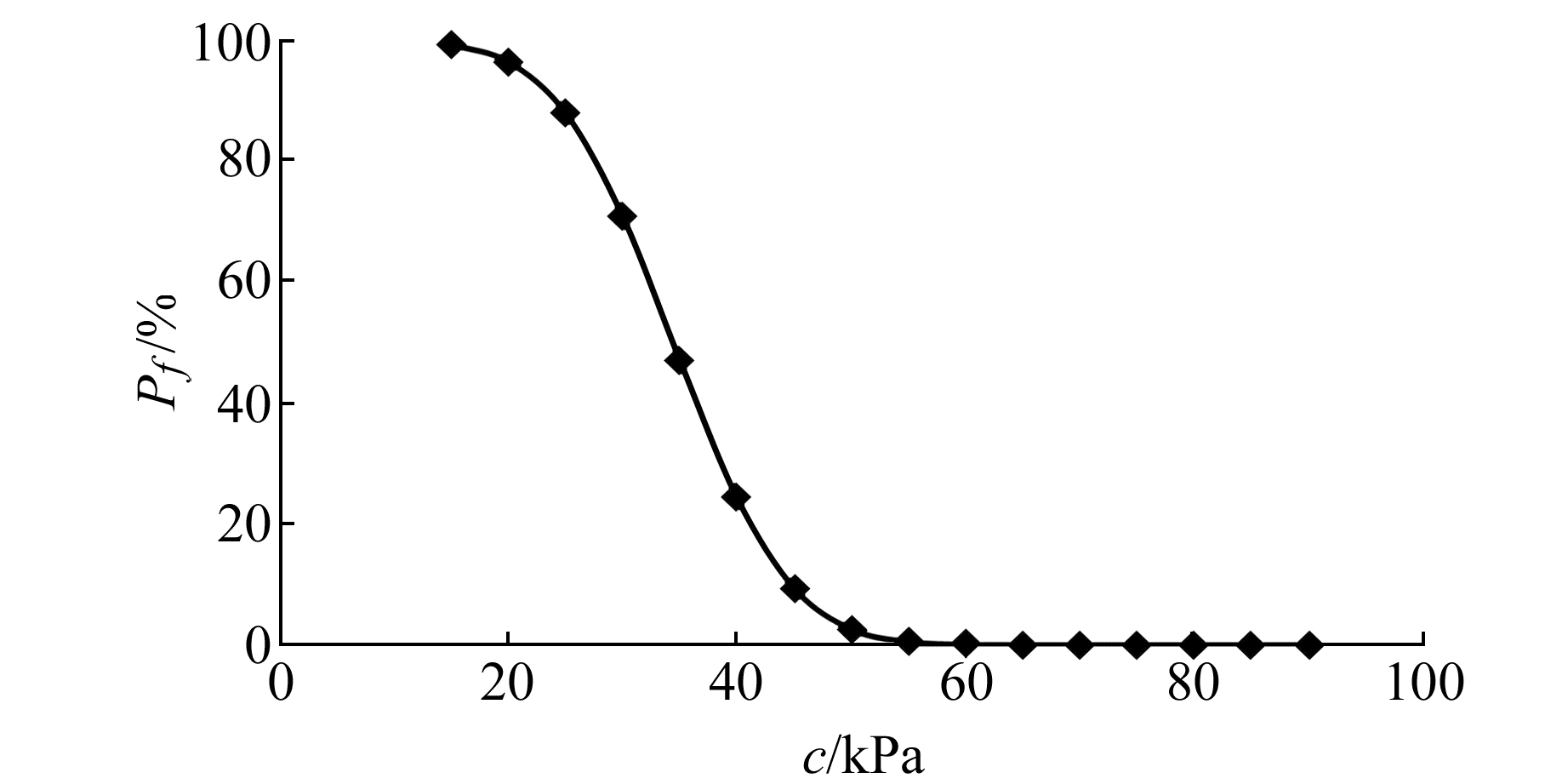
4.2 敏感性分析图 3为滑动面取不同粘聚力(c)时的边坡失稳概率变化曲线。该曲线表明,随着c值的增加失稳概率先缓慢减小,当c>22 kPa时失稳概率迅速降低,说明c值对边坡的失稳概率影响较大。在其他参数不变的情况下,c < 15 kPa时失稳概率达100%。基于前文失稳概率的稳定性判定准则,c < 22 kPa时边坡失稳,c>50 kPa时边坡稳定。图 4为滑动面取不同内摩擦角(φ)时边坡的失稳概率变化曲线。该曲线表明,随着φ值的增加,边坡失稳概率近乎线性减小;当φ>55°时边坡失稳概率小于5%,即边坡达到稳定。
|
图 3 不同c值条件下的失稳概率 Fig. 3 Failure probability under the circumstance of different c values |

|
图 4 不同φ值条件下的失稳概率 Fig. 4 Failure probability under the circumstance of different φ values |
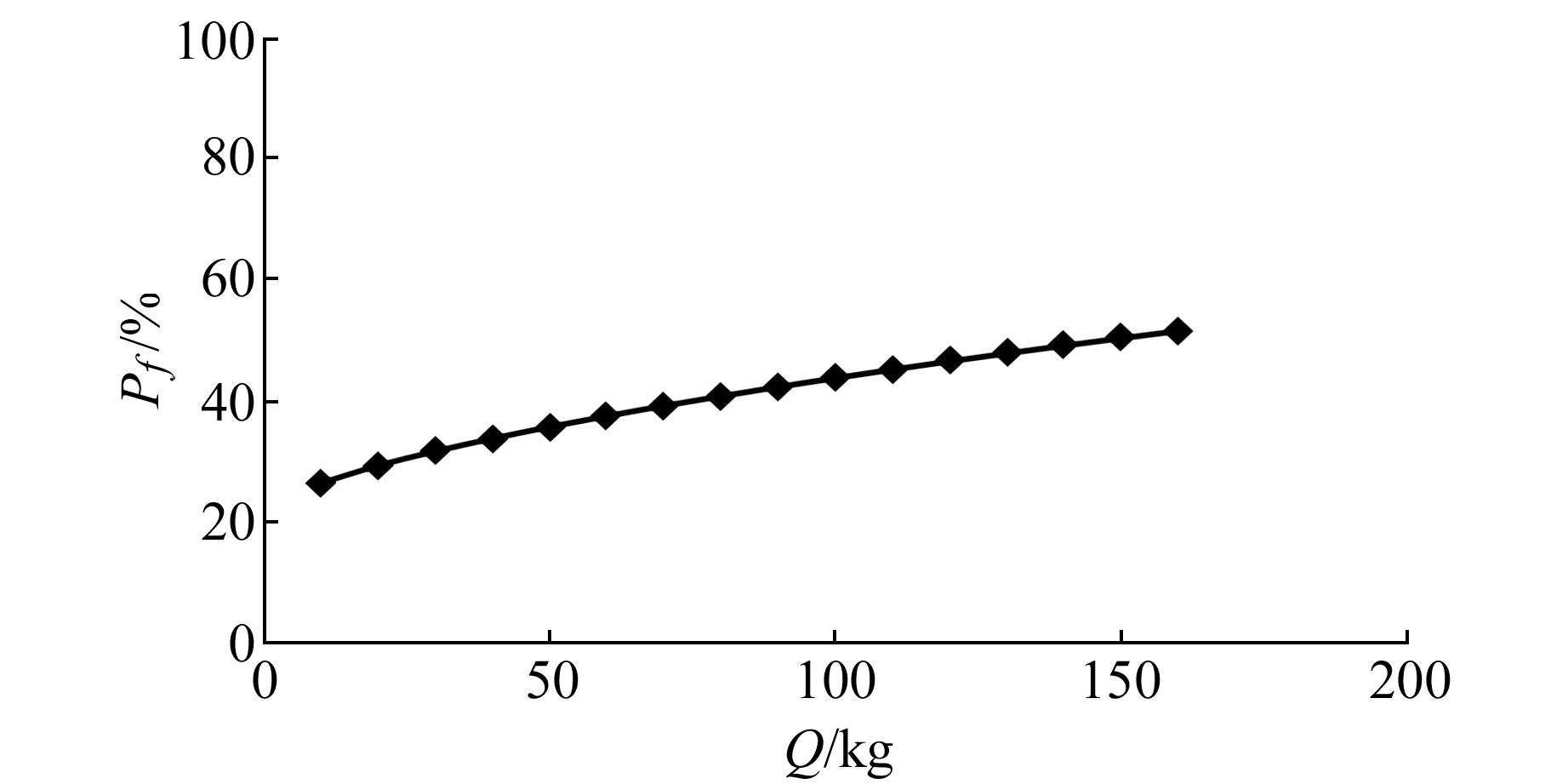
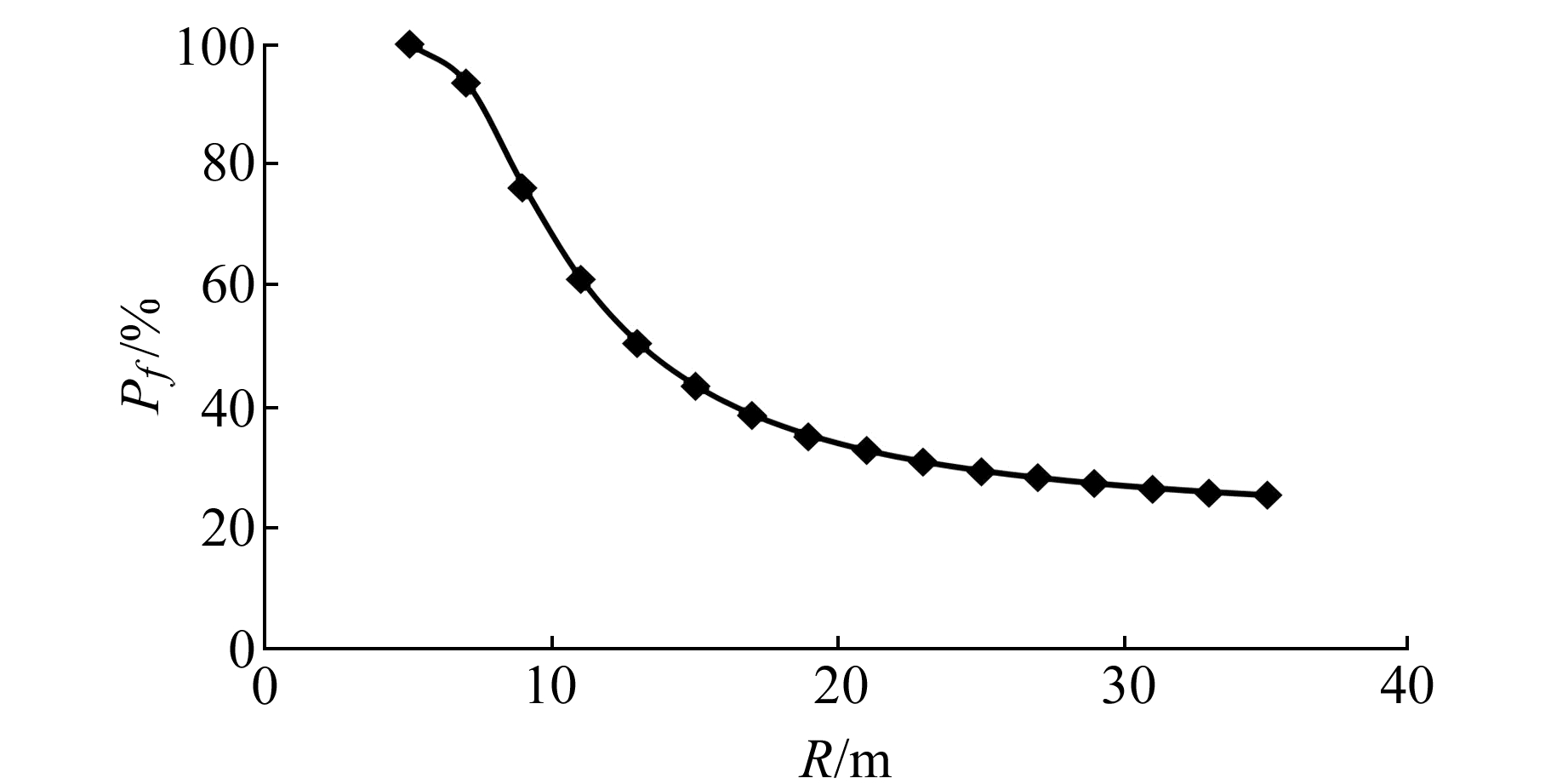
图 5为不同炸药量条件下的边坡失稳概率变化曲线。该曲线表明,随着炸药量的增加,边坡失稳概率不断增大,当单孔药量从10 kg增大到160 kg后,失稳概率由26.24%增大到51.72%,增幅为97.10%。图 6为不同爆心距(R)条件下的失稳概率变化曲线。该曲线表明,随着爆心距的增加失稳概率减小,当R < 20 m时,边坡的失稳概率减小的速度很快;R>20 m后,边坡的失稳概率减小的幅度变小。
|
图 5 不同炸药量条件下的失稳概率 Fig. 5 Failure probability under the circumstance of different explosive mass |
|
图 6 不同爆心距条件下的失稳概率 Fig. 6 Failure probability under the circumstance of different distance to blasting center |
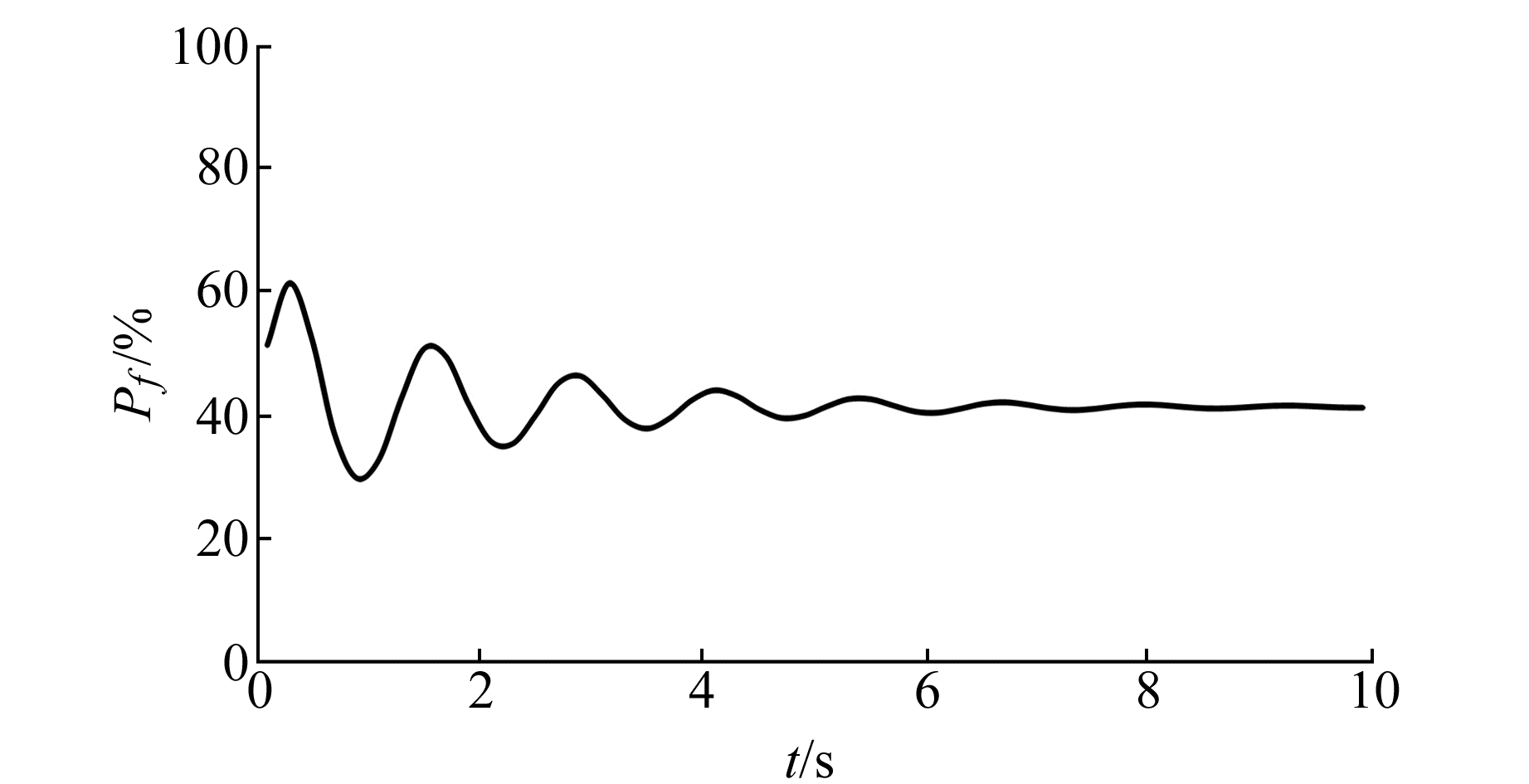
图 7为考虑爆破振动时效性的边坡失稳概率变化曲线。考虑爆破荷载后的最大失稳概率为30.73%,最小失稳概率为14.67%,即在爆破振动影响下的边坡失稳概率变化范围为16.06%。根据前文计算结果可知,不考虑爆破荷载时的边坡失稳概率为20.54%,爆破荷载使边坡失稳概率增大49.61%,即爆破对边坡的稳定性有明显影响,稳定状态也由基本稳定转变为欠稳定。所以,在边坡易滑塌区要严格控制爆破作业,并加强爆破区域边坡变形的监测和防治工作,以免造成人员伤亡和财产损失。随着爆破振动加速度的衰减,边坡的失稳概率逐渐减小并趋于同不考虑爆破荷载时的失稳概率一致。另外,随着爆破振动作用周期增加,爆破振动影响时间延长,也相应加大了边坡失稳的危险性。图 7曲线表明,单次爆破振动的影响时间约为6 s。
|
图 7 随时间变化的失稳概率 Fig. 7 Failure probability changed with time |
1) 基于可靠度和极限平衡方法,并考虑爆破荷载的作用,建立了边坡失稳概率计算方法。通过算例分析证明了该方法的合理性。
2) 以重庆万州某小区顺层高切坡为例的计算结果表明,裂隙水压力和爆破荷载对边坡的稳定性影响最大,相比较而言裂隙水压力影响更为显著。
3) 随着粘聚力和内摩擦角的增加,边坡失稳概率逐渐减小。其中,粘聚力对边坡的失稳概率影响尤为敏感;随着内摩擦角的增加,边坡失稳概率近乎线性减小。
4) 增加炸药量使边坡失稳概率不断增大,当单孔药量从10 kg增大到160 kg后,边坡失稳概率增幅达97.10%;失稳概率随着爆心距的增加呈非线性减小,当爆心距小于20 m时,边坡失稳概率减小的速度很快,爆心距超过20 m后边坡失稳概率减小的幅度变小。
5) 考虑爆破振动的时效性,边坡的失稳概率变化范围为16.06%,爆破荷载使边坡的失稳概率增大49.61%,单次爆破振动的影响时间约6 s。
| [1] |
彭兴, 李典庆, 曹子君, 等. 基于蒙特卡洛模拟的岩质边坡可靠度设计方法[J]. 岩石力学与工程学报, 2016, 35(增2): 3794-3804 (Peng Xing, Li Dianqing, Cao Zijun, et al. Reliability-Based on Design Approach of Rock Slopes Using Monte Carlo Simulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S2): 3794-3804)
(  0) 0) |
| [2] |
蒋水华, 祁小辉, 曹子君, 等. 基于随机响应面法的边坡系统可靠度分析[J]. 岩土力学, 2015, 36(3): 809-818 (Jiang Shuihua, Qi Xiaohui, Cao Zijun, et al. System Reliability Analysis of Slope with Stochastic Response Surface Method[J]. Rock and Soil Mechanics, 2015, 36(3): 809-818)
(  0) 0) |
| [3] |
唐小松, 李典庆, 曹子君, 等. 有限数据条件下边坡可靠度分析的Bootstrap方法[J]. 岩土力学, 2016, 37(3): 893-911 (Tang Xiaosong, Li Dianqing, Cao Zijun, et al. A Bootstrap Method for Analyzing Slope Reliability Based on Limited Shear-Strength Parameter Data[J]. Rock and Soil Mechanics, 2016, 37(3): 893-911)
(  0) 0) |
| [4] |
李维光, 张继春. 爆破振动作用下顺层岩质边坡稳定性分析[J]. 爆炸与冲击, 2007, 27(5): 426-430 (Li Weiguang, Zhang Jichun. Study on Rock Mass Bedding Slope Stability under Blast Seism[J]. Explosion and Shock Waves, 2007, 27(5): 426-430 DOI:10.3321/j.issn:1001-1455.2007.05.008)
(  0) 0) |
| [5] |
王智德, 夏元友, 周雄, 等. 顺层岩质边坡爆破的振动控制及损伤特性[J]. 爆炸与冲击, 2017, 37(1): 27-36 (Wang Zhide, Xia Yuanyou, Zhou Xiong, et al. Blasting Vibration Control and Damage Characteristic of Bedding Rock Slopes[J]. Explosion and Shock Waves, 2017, 37(1): 27-36)
(  0) 0) |
| [6] |
崔铁军, 马云东, 王来贵. 边坡爆破高度对边坡稳定性的影响[J]. 安全与环境学报, 2017, 17(3): 896-900 (Cui Tiejun, Ma Yundong, Wang Laigui. Simulated Study on the Influence of the Slope Blasting Height on the Slope Stability[J]. Journal of Safety and Environment, 2017, 17(3): 896-900)
(  0) 0) |
| [7] |
张飞, 孟祥甜, 李铸峰, 等. 震动波传播衰减特性模拟[J]. 辽宁工程技术大学学报:自然科学版, 2014, 33(8): 1103-1107 (Zhang Fei, Meng Xiangtian, Li Zhufeng, et al. Transmission Characteristics of Shock Wave in Rock Slope[J]. Journal of Liaoning Technical University:Natural Science, 2014, 33(8): 1103-1107)
(  0) 0) |
| [8] |
钟冬望, 陈江伟, 余刚. 边坡爆破振动传播规律的试验研究[J]. 武汉科技大学学报, 2010, 33(3): 332-336 (Zhong Dongwang, Chen Jiangwei, Yu Gang. Experimental Study of Propagation of Slope Blasting Vibration[J]. Journal of Wuhan University of Science and Technology, 2010, 33(3): 332-336 DOI:10.3969/j.issn.1674-3644.2010.03.026)
(  0) 0) |
| [9] |
张继春, 郭学彬, 郑爽英, 等. 顺层边坡岩体的爆破振动特性试验研究[J]. 地下空间与工程学报, 2005, 1(7): 1041-1044 (Zhang Jichun, Guo Xuebin, Zheng Shuangying, et al. Experimental Study on Vibration Characteristic of Rock Mass Blasting at Layered Slope[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(7): 1041-1044)
(  0) 0) |
| [10] |
桂劲松, 康海贵. 结构可靠度分析的响应面法及其Matlab实现[J]. 计算力学学报, 2004, 21(6): 683-687 (Gui Jinsong, Kang Haigui. Response Surface Method for Structural Reliability Analysis and Its Realization with Matlab[J]. Chinese Journal of Computational Mechanics, 2004, 21(6): 683-687 DOI:10.3969/j.issn.1007-4708.2004.06.008)
(  0) 0) |
| [11] |
贡金鑫, 魏巍巍. 工程结构可靠性设计原理[M]. 北京: 机械工业出版社, 2007 (Gong Jinxin, Wei Weiwei. Principles of Reliability Design for Engineering Structure[M]. Beijing: China Machine Press, 2007)
(  0) 0) |
| [12] |
SL378-2007, 水工建筑物地下开挖工程施工规范[S].北京: 中国水利水电出版社, 2008 (SL378-2007, Construction Specification on Underground Excavating Engineering of Hydraulic Structures[S]. Beijing: China Water & Power Press, 2008)
(  0) 0) |
| [13] |
张倬元, 王士天, 王兰生. 工程地质分析原理[M]. 北京: 地质出版社, 2009 (Zhang Zhuoyuan, Wang Shitian, Wang Lansheng. Principles of Engineering Geology[M]. Beijing: Geological Publishing House, 2009)
(  0) 0) |
2. Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Road, Wuhan 430071, China;
3. School of River & Ocean Engineering, Chongqing Jiaotong University, 69 Xuefu Road, Chongqing 400074, China
 2019, Vol. 39
2019, Vol. 39

