2. 中国地震局工程力学研究所地震工程与工程振动重点实验室,哈尔滨市学府路29号, 150080
随着我国高速铁路的迅猛发展,其运行安全问题越来越受到重视。高速铁路地震预警作为高速铁路防灾子系统中的重要部分,对于高速铁路运行安全具有重要作用[1]。当破坏性地震到来时,高速铁路紧急处置范围的快速确定需要依赖地震预警的快速定位结果[2]。目前,高速铁路地震监测台站沿线路布设,分布极为稀疏,并成条带状,因此,准确的单台定位方法研究显得尤为重要[3]。偏振分析方法是计算震中方位角的常用方法。Flinn[4]于1965年提出基于时域的偏振分析方法用于确定主偏振方向。在地震预警的研究与应用中,Lockman等[5]利用美国南加州的50次地震数据,验证了偏振分析方法计算震中方位角的有效性; 周彦文[6]采用偏振分析方法,利用中国山东省的测震记录计算震中方位角; 马强[7]采用移动时间窗偏振分析,利用中国福建省的测震记录计算震中方位角; Noda等[8]采用位移记录首脉冲的时间窗长代替固定的1.1 s时间窗来估计震中方位角,研究结果表明,方位角计算的正确率提高了28%;马亮[9]基于强震动观测加速度记录,采用偏振分析方法计算震中方位角,结果显示,方位角计算的误差远高于马强和周彦文[6-7]基于测震记录计算结果的误差。由此可见,计算震中方位角特别是利用强震动观测记录计算震中方位角时,有影响震中方位角计算结果精度的因素存在,如计算时间窗、记录形式等,需要探明。
本文在前人研究的基础上,以提高计算震中方位角的准确性为目标,基于KiK-net强震动观测记录数据,研究记录参量(加速度、速度、位移)、计算时间窗、滤波频带对偏振分析法计算震中方位角的影响。
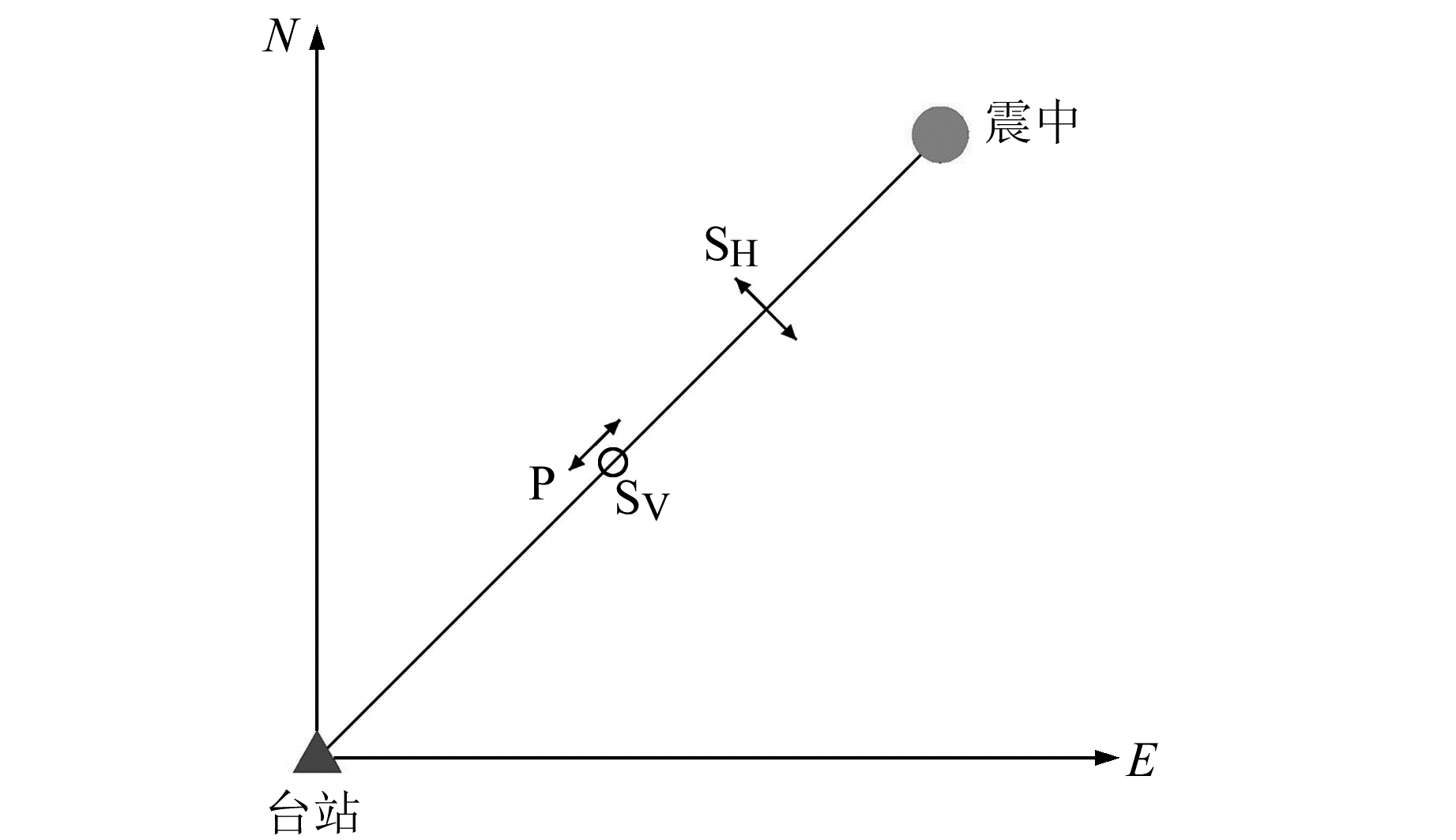
1 方法原理地震波分为体波和面波,体波包括纵波(P波)和横波(S波),面波包括瑞雷波和勒夫波,各种波型均有其自身的偏振特性。纵波(P波)呈线性偏振,且质点振动方向与波传播方向一致;横波(S波)的振动虽然也呈线性偏振,但质点振动方向垂直于波的传播方向,S波又分为SH波和SV波,SH波在水平面内振动,SV波在铅垂平面内振动(图 1)[10-12]。
|
图 1 地震波极化特性示意图 Fig. 1 Sketch map of polarization characteristics of seismic wave |
偏振分析法就是利用不同波在传播过程中的不同振动特性进行震中方位角的确定以及不同地震波的捡拾的理论方法[13]。偏振分析法的实质是通过坐标变换使质点振动的主方向落在极化主轴上,从而计算方位角和入射角,并利用不同波的不同偏振特性进行波的震相识别和震相分离,以及降噪的处理[11-13]。根据地震波中不同类型震相的特点,保留目标震相偏振方向的振动,压制其他方向的振动,这种方法称为偏振滤波(极化滤波)[4, 7, 11, 14]。
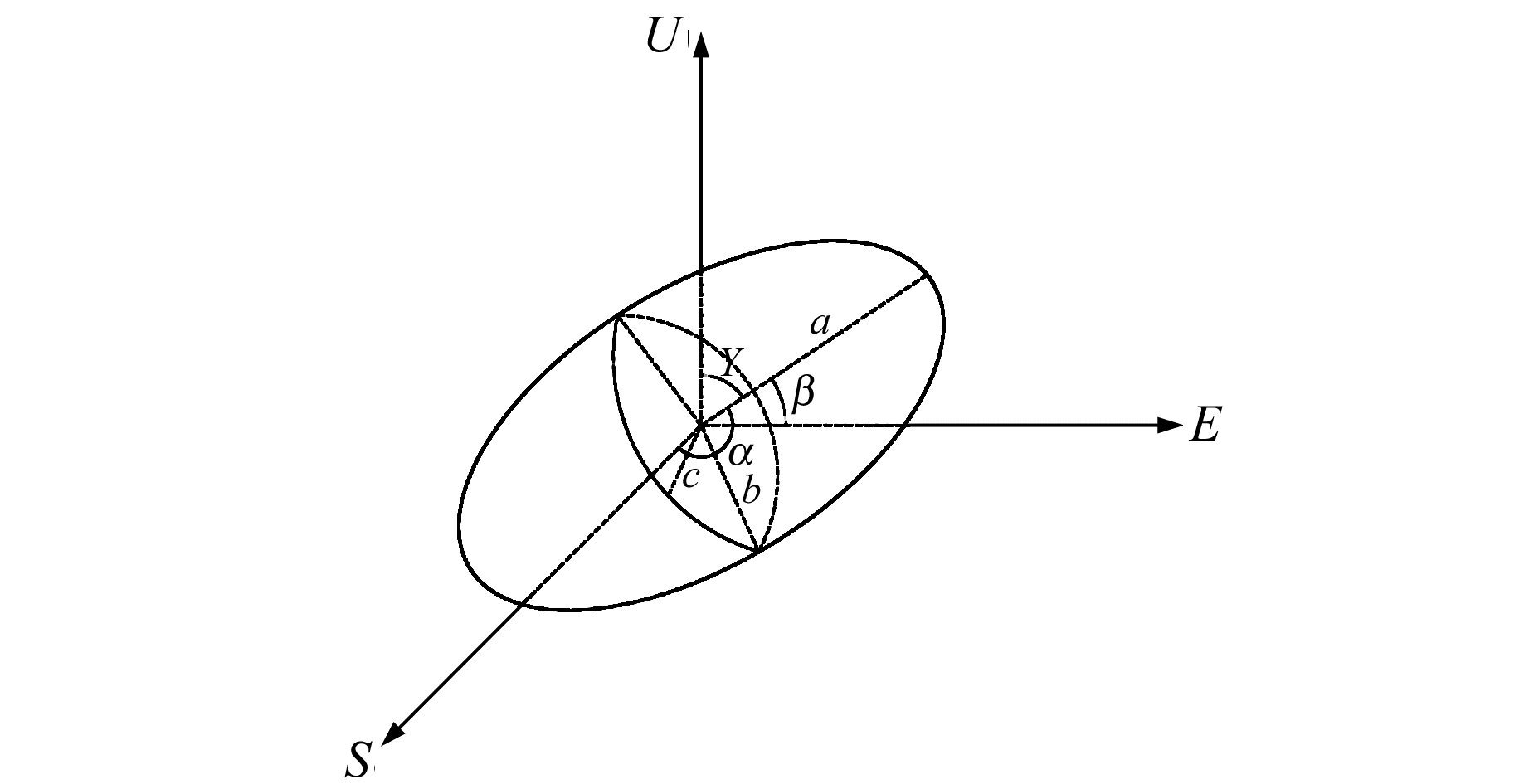
如图 2所示,每一个台站都有东西、南北和上下3个分量的拾振器。理想条件下,当一次地震的P波传播经过台站时,台站三分量记录到的该点介质的振动轨迹为一个空间椭球,此椭球长轴与正北的夹角即为震中方位角(角α)。求取椭球长轴方向主要有3种方法:传递函数法、斜极化法和协方差矩阵法[10],本文采用协方差矩阵法进行偏振分析。
|
图 2 质点在三维空间偏振的轨迹示意图 Fig. 2 Sketch map of three-dimensional particle polarization trajectory |
协方差矩阵法所用的滤波器属于一种解析几何方法。通过坐标变换,把方程和几何图形对应起来。计算协方差矩阵的二次型,得到一个椭球型空间曲线方程。
对于三分量地震记录,选取一个时窗作为研究范围,即选取三分量记录中N个样点时窗(T1,T2),每个点的3个分量值X1、Y1、Z1在(T1,T2)时窗内的均值分别为:
| $ {m_x} = \frac{1}{N}\sum\limits_{i = {N_1}}^{{N_2}} {{x_i}, {m_y} = \frac{1}{N}\sum\limits_{i = {N_1}}^{{N_2}} {{y_i}, {m_z} = \frac{1}{N}\sum\limits_{i = {N_1}}^{{N_2}} {{z_i}} } } $ |
式中,(N2-N1)Δt=T2-T1,Δt是采样率;N=N2-N1+1。进而构造一个协方差矩阵:
| $ {\mathit{\boldsymbol{M}}_C} = \frac{1}{N}\left[{\begin{array}{*{20}{c}} {\sum {{A^2}} }&{\sum {AB} }&{\sum {AC} }\\ {\sum {BA} }&{\sum {{B^2}} }&{\sum {BC} }\\ {\sum {CA} }&{\sum {CB} }&{\sum {{C^2}} } \end{array}} \right] $ | (1) |
式中, ∑为
由协方差矩阵可以得到3个特征值λ1、λ2、λ3(λ1>λ2>λ3)和3个特征向量Λ1、Λ2、Λ3,它们分别由|MC-λE|=0、MCΛ=λΛ确定, 其中E为单位矩阵。为纯线性偏振时,λ1≠0, λ2=λ3=0,例如P波、SH波、勒夫波;为纯椭圆偏振时,λ1=λ2≠0, λ3=0,例如瑞雷波。实际的地震波3个特征值一般都非零且不等,偏振为椭球形[15]。
协方差矩阵的最大特征值λ1对应的特征向量Λ1为主特征向量,在笛卡尔坐标系(X, Y, Z)中由3个标量坐标(ΛX, ΛY, ΛZ)唯一确定。而主特征向量Λ1在空间的方向是由它的3个方向余弦cosα(t)、cosβ(t)及cosγ(t)所确定的,即α(t)、β(t)、γ(t)分别为主极化方向与坐标轴X、Y、Z的夹角。根据ΛX2+ΛY2+ΛZ2=1的关系及相应的空间几何关系可以证明,主特征向量Λ1的3个方向余弦恰好就等于它的3个标量坐标,即
| $ \left\{ {\begin{array}{*{20}{c}} {\cos \alpha (t) = {\mathit{\Lambda }_X}}\\ {\cos \beta (t) = {\mathit{\Lambda }_Y}}\\ {\cos \gamma (t) = {\mathit{\Lambda }_Z}} \end{array}} \right. $ | (2) |
这也就说明了主特征向量代表质点偏振的主方向。一旦极化椭球的偏振主轴确定以后,相应的震中方位角就确定了[7]。则震中方位角可用公式(3)进行计算:
| $ {\rm{azi}} = {\rm{ta}}{{\rm{n}}^{-1}}(\frac{{{\mathit{\Lambda }_Z}{\rm{sign}}({\mathit{\Lambda }_X})}}{{{\mathit{\Lambda }_Y}{\rm{sign}}({\mathit{\Lambda }_X})}}) $ | (3) |
本文从日本防灾科学技术研究所(NIED)的KiK-net强震观测台网中下载449组三分量强震动记录。选择的原则有两条:一是考虑实际地震预警中可能造成的破坏,选取震级6.0以上浅源地震(震源深度范围0~30 km);二是考虑到信噪比可能的影响,尽量选择高信噪比的记录,选取的地震的震中均在日本岛上,震中距0~100 km。记录中包含了66组2003-05-26发生在日本本州岛东北地区的7.0级地震的三分量记录、108组2004-10-23发生在日本新泻的6.8级地震三分量记录、82组2006-06-12发生在日本九州岛的6.2级地震三分量记录、77组2007-07-16发生在日本新泻的6.8级地震的三分量记录和115组2008-06-14发生在日本岩手县南部的7.2级地震三分量记录。
偏振分析法计算震中方位角步骤为:
1) 对三分量记录进行基线校正,并进行数字滤波,滤波频带0.1~20 Hz;
2) 通过积分获得速度和位移记录;
3) 利用STA/LTA方法结合AIC方法确定P波到时点[7];
4) 读取P波到时点后固定窗长(定义窗长为选定记录的时间长度)的三分量记录;
5) 利用协方差矩阵法求取震中方位角,同时,根据台站的经纬度和震中的经纬度可以得到实际方位角。
3 影响因素分析偏振分析法计算震中方位角受哪些因素影响,这个问题具有重要的研究价值,可在实际工作中应用于单台地震预警定位服务。本文从使用记录的参量、计算时间窗和滤波频带3个方面对偏振分析方法计算方位角的影响因素进行讨论。
3.1 参量形式的影响为研究参量形式对偏振分析计算方位角的影响,本文分别采用了加速度记录、速度记录和位移记录计算各个台站的震中方位角,计算结果如图 3、图 4所示,时窗长度为1.1 s。

|
图 3 计算方位角与实际方位角散点图 Fig. 3 Scatter diagram of actual azimuth and calculated azimuth |

|
图 4 计算方位角残差直方图 Fig. 4 Histogram of azimuthal residuals |
图 3为不同记录形式计算方位角和实际方位角的散点图,图 4为方位角残差直方图。由图 3可知,偏振分析法计算方位角与实际方位角呈明显的线性相关性;对于散点图中的位于左上端点和右下端点附近的点,可以进行相关的修正[9]得到合理的结果,再给出残差(残差=实际方位角-计算方位角)的直方图。由图 4可知,3种记录形式获得的震中方位角的误差有很大的差别。加速度记录计算的结果误差最大,而位移记录计算的结果误差最小。
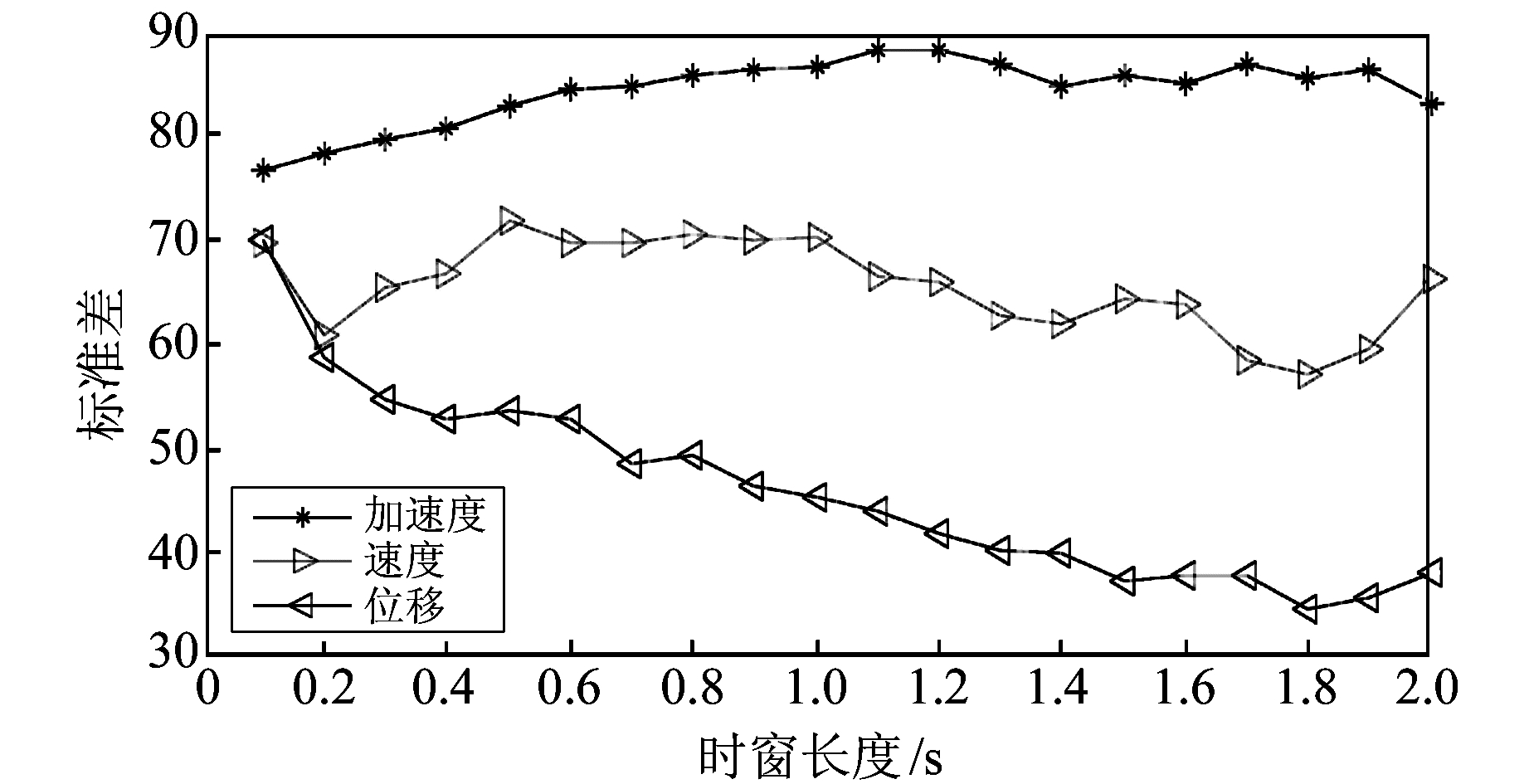
3.2 时窗长度的影响时窗长度是震中方位角计算中一个非常重要的参数,时窗长度选择过短就会放大随机干扰的影响,而时窗长度选择过长则会将其余震相混杂在初至P波内, 影响到结果的合理性。为此,本文计算了时窗长度0.1~2.0 s范围内的震中方位角,并进行误差分析。
图 5给出偏振分析法计算方位角残差标准差随时窗长度的变化曲线。由图可知,加速度、速度和位移记录得到的标准差都是随窗长变化而波动的,但是在1 s左右位移记录计算方位角的残差标准差得到较为理想的结果。
|
图 5 计算方位角残差标准差随时窗长度变化的曲线 Fig. 5 Curves of azimuth residual's standard deviation vary with time window length |
图 6给出了15°、30°和45°偏差所占比例(即15°、30°和45°偏差范围记录占总记录的百分比,其中偏差均以0为中心)随窗长的变化曲线。从中可知,加速度和速度记录得到的结果都是波动的,没有随窗长增加而出现单调变化的规律;位移记录计算方位角偏差所占比例随着窗长的变化最终趋向于某一确定值。在偏差为15°时,偏差所占比例在1 s左右趋向于58%;在偏差为30°时,偏差所占比例在1 s左右趋向于80%;在偏差为45°时,偏差所占比例在1 s左右趋向于88%。同时考虑到地震预警的时效性,在计算时间窗长度大于1 s时,对计算方位角的提高已经不显著, 故建议选取时窗长度为1 s。

|
图 6 偏差所占比例随窗长变化的曲线 Fig. 6 Curves of deviation percentage vary with time window length |
在实际的地震动记录中,通常含有噪声,常采用滤波的方法来消除噪声的干扰,不同的滤波频带具有不同的滤波效果。位移记录的主频为低频,是否意味着低频对偏振分析法计算方位角是重要的影响因素?本节中分不同滤波频带范围,利用偏振分析方法求取震中方位角,并进行误差分析,研究滤波频带对计算方位角的影响。
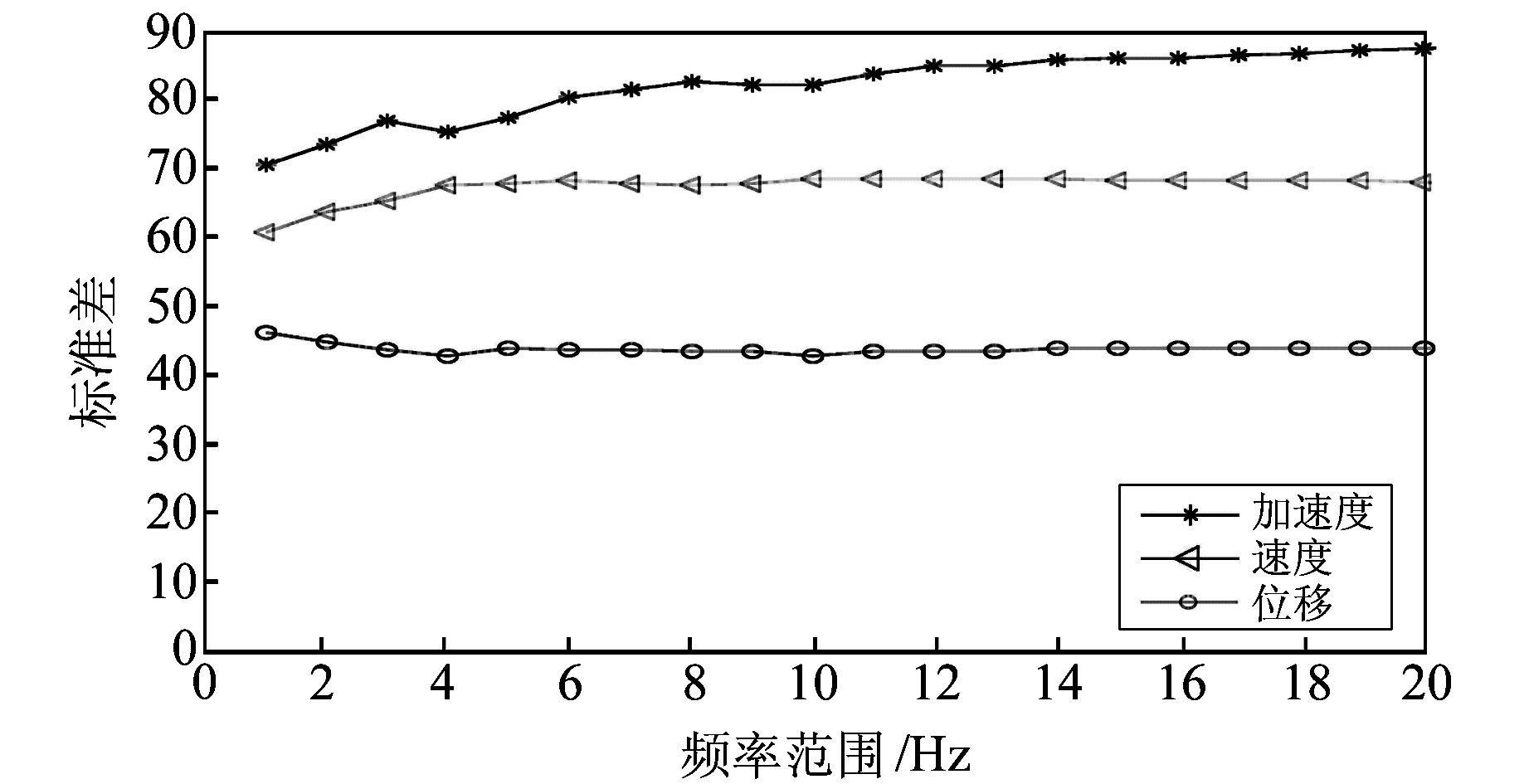
利用上节数据,对449组记录采用二阶Butterworth因果带通滤波器滤波,滤波频带分别选取0.1~1 Hz、0.1~2 Hz、…、0.1~20 Hz,滤波后的加速度一次积分得到速度记录、二次积分得到位移记录,采用位移记录利用偏振分析法求得震中方位角,时间窗大小采用§1.2中确定的可选时窗1 s,结果如图 7、图 8所示。
|
图 7 标准差随滤波频带范围变化的曲线 Fig. 7 Curves of standard deviation vary with filter band |
|
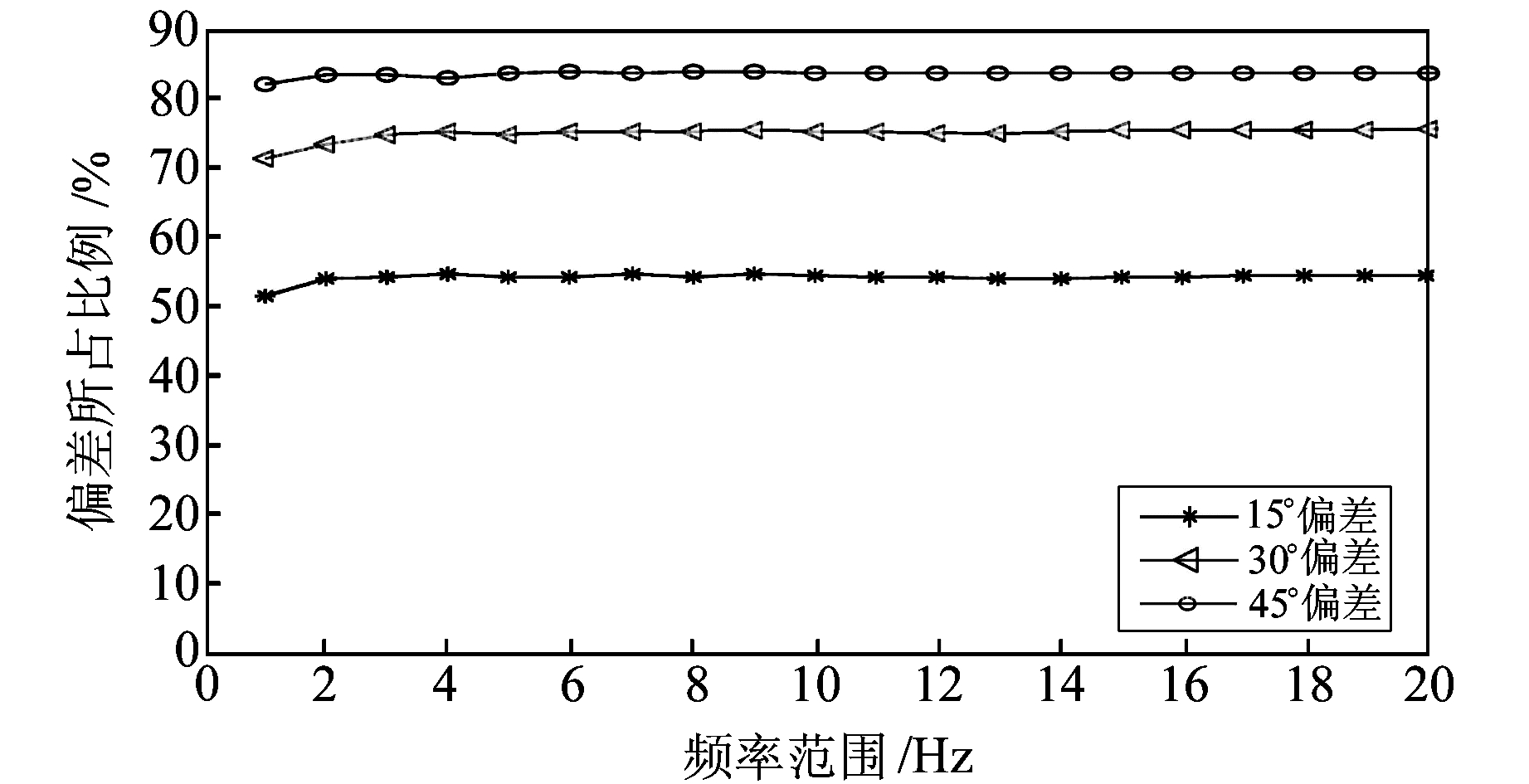
图 8 偏差所占比例随滤波频带变化的曲线 Fig. 8 Curves of deviation percentage vary with filter band |
图 7为方位角残差的标准差随滤波频带方位角的变化,图 8为方位角偏差所占比例随滤波频带的变化。由图 7可知,位移记录计算方位角残差与加速度记录和速度记录计算方位角相比有着最小的标准差;随着滤波频带的变化,位移记录的标准差是波动的,在0.1~4 Hz滤波频带下的标准差最小为42.52,且在0.1~4 Hz以后标准差趋于确定值。由图 8可知,位移记录计算得到的方位角偏差所占比例随着滤波频带范围的增加而波动,在0.1~5 Hz滤波频带下45°偏差所占比例最大为85%,且0.1~5 Hz以后趋于确定值。强震动观测关注的天然地震信号的频带范围为20 Hz以下的地震信号,为尽可能多地保留地震信号,故建议上限采用20 Hz。0.1~20 Hz是我国强震动观测数据的通用滤波频带,可用于去除噪声,消除加速度二次积分为位移出现的低频漂移问题。故本文推荐采用与我国强震动观测数据相同的滤波频带0.1~20 Hz。
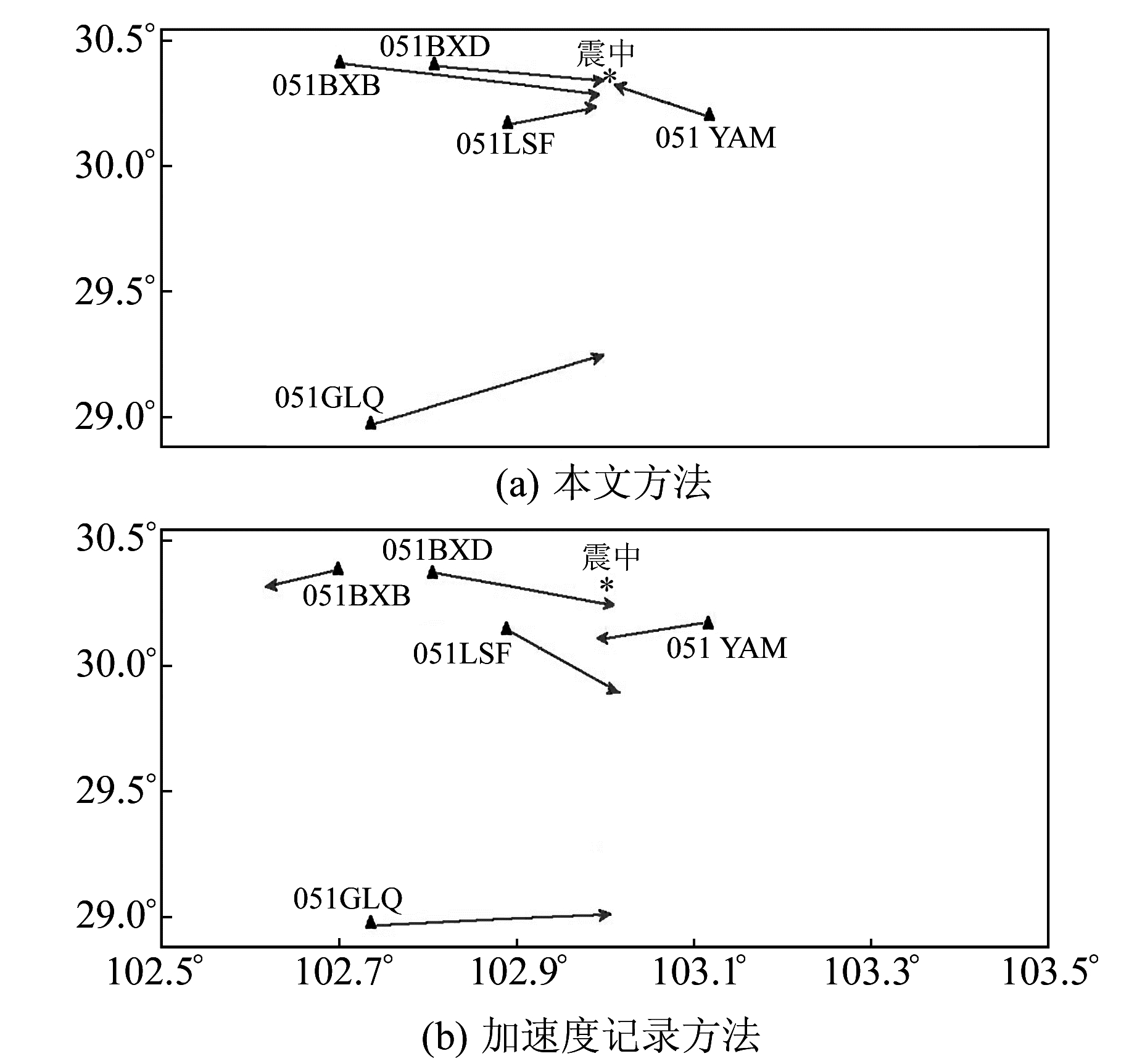
4 震例验证为验证该方法的可靠性,选取2013-04-23芦山7.0级地震作为震例。选取台站的信息如表 1所示。5个台站记录到的数据采用文中方法计算得到的方位角示意图如图 9(a)所示,采用加速度记录方法计算得到的方位角示意图如图 9(b)所示,其中五角星为震中位置,三角形为台站所在位置,射线为计算方位角所在方向。
|
|
表 1 台站基本信息 Tab. 1 List ofbasic information of the station |
|
图 9 计算方位角示例 Fig. 9 The example of azimuth |
由图 9(a)与图 9(b)对比可知,采用本文推荐的位移记录、时间窗长度1 s、滤波频带0.1~20 Hz计算的方位角的结果,明显优于采用加速度记录、时间窗长度1 s、滤波频带0.1~20 Hz的结果。
5 结语本文基于日本KiK-net强震动观测记录,以提高计算震中方位角的准确性为目标,研究了记录参量(加速度、速度和位移)、计算时间窗和滤波频带对偏振分析计算震中方位角的影响,并通过一个国内的震例进行验证,研究结论如下:
1) 当采用位移记录时,计算方位角与实际方位角的线性相关性较加速度记录和速度记录取得的结果更高。
2) 计算时间窗取1 s时,计算方位角的偏差最小。
3) 当滤波频带为0.1~20 Hz时,计算方位角的结果较好。
因此,本文建议,在高速铁路地震预警中,选取滤波频带0.1~20 Hz、位移记录、计算时间窗1 s,采用偏振分析方法计算震中方位角。
当然,利用偏振分析法确定震中方位角有一定的局限性。首先,利用单台偏振分析法确定震中方位角利用的信息有限,精度相对多台而言要低;其次,该方法的准确性很大程度上要求单个台站自身安装要严格按照规范,安装方位对计算结果的影响明显;最后,我国与日本的台网建设有很大区别,我国建台单位较为分散,建台的质量很大程度上取决于建台工作人员的业务水平,而日本是委托专门的第三方仪器公司,建台质量和售后均由专门的公司负责,数据质量较高。
对于目前高速铁路这种呈线状分布的台阵不宜利用多台定位,采用本文方法确定震中方位角具有更好的时效性,且具有一定的精度。所以,作者建议在高速铁路地震预警系统中采用该方法确定震中方位角。同时建议由专业的巡检和维修公司对沿线地震仪器进行摸底和技术维护,更新最新的建台信息。
| [1] |
范涛.数字滤波与偏振分析在强震动数据处理中的应用[D].哈尔滨: 中国地震局工程力学研究所, 2014 (Fan Tao.Digital Filter and Polarization Analysis's Application of Data Processing of Strong Motion Records[D]. Harbin: Institute of Engineering Mechanics, CEA, 2014)
(  0) 0) |
| [2] |
宋晋东, 李山有, 马强. 日本新干线地震监测与预警系统[J]. 世界地震工程, 2012, 28(4): 1-10 (Song Jindong, Li Shanyou, Ma Qiang. Overview on Earthquake Monitoring and Early Warning System for High-Speed Railway(Shinkansen) in Japan[J]. World Earthquake Engineering, 2012, 28(4): 1-10 DOI:10.3969/j.issn.1007-6069.2012.04.001)
(  0) 0) |
| [3] |
宋晋东.高速铁路运行控制用地震动参数及单台地震预警技术研究[D].哈尔滨: 中国地震局工程力学研究所, 2013 (Song Jindong. Research on Seismic Ground Motion Indices for Operation Control and Single Station Earthquake Early Warning Applied for High-Speed Railway[D]. Harbin: Institute of Engineering Mechanics, CEA, 2013)
(  0) 0) |
| [4] |
Flinn E. Signal Analysis Using Rectilinearity and Direction of Particle Motion[J]. Proceedings of the IEEE, 1965, 53(12): 1874-1876 DOI:10.1109/PROC.1965.4462
(  0) 0) |
| [5] |
Lockman A B, Allen R M. Single-Station Earthquake Characterization for Early Warning[J]. Bulletin of the Seismological Society of America, 2005, 95(6): 2029-2039 DOI:10.1785/0120040241
(  0) 0) |
| [6] |
周彦文.基于单台P波记录的早期地震预警方法研究[D].兰州: 中国地震局兰州地震研究所, 2008 (Zhou Yanwen. Study on the Early Warning System Method Based on a Single Station's P Wave Record[D]. Lanzhou: Lanzhou Institute of Seismology, CEA, 2008)
(  0) 0) |
| [7] |
马强.地震预警技术研究及应用[D].哈尔滨: 中国地震局工程力学研究所, 2008 (Ma Qiang. Study and Application on Earthquake Early Warning[D]. Harbin: Institute of Engineering Mechanics, CEA, 2008)
(  0) 0) |
| [8] |
Noda S, Yamamoto S, Sato S. New Method for Estimating Earthquake Parameters for Earthquake Early Warning[J]. QR of RTRI, 2012, 53(2): 102-106 DOI:10.2219/rtriqr.53.102
(  0) 0) |
| [9] |
马亮.用于地震预警的单台定位技术研究[D].哈尔滨: 中国地震局工程力学研究所, 2013 (Ma Liang. Research on Earthquake Location Using Single Station for Earthquake Early Warning[D]. Harbin: Institute of Engineering Mechanics, CEA, 2013))
(  0) 0) |
| [10] |
杜玉静.三分量地震极化滤波[D].西安: 长安大学, 2010 (Du Yujing. Polarization Filter for Three-Component Seismic Data[D]. Xi'an: Chang'an University, 2010)
(  0) 0) |
| [11] |
肖梅.三分量地震极化滤波与波场分离方法研究[D].西安: 长安大学, 2005 (Xiao Mei.Three-Component Seismic's Wave Polarization Analysis and Wavefield Separation[D]. Xi'an: Chang'an University, 2010)
(  0) 0) |
| [12] |
Jurkevics A. Polarization Analysis of Three-Component Array Data[J]. Bulletin of the Seismological Society of America, 1988, 78(5): 1725-1743
(  0) 0) |
| [13] |
李铜基. 极化滤波[J]. 海洋技术, 1996, 15(4): 130-137 (Li Tongji. Polarization Analysis[J]. Ocean Technology, 1996, 15(4): 130-137)
(  0) 0) |
| [14] |
Reading A M, Mao W, Gubbins D. Polarization Filtering for Automatic Picking of Seismic Data and Improved Converted Phase Detection[J]. Geophysical Journal International, 2001, 147(1): 227-234 DOI:10.1046/j.1365-246X.2001.00501.x
(  0) 0) |
| [15] |
林建民, 杨微, 陈蒙, 等. 偏振分析法在地震信号检测中的应用[J]. 中国地震, 2012, 28(2): 133-143 (Lin Jianmin, Yang Wei, Chen Meng, et al. The Application of Polarization Analysis in Seismic Signaldetection[J]. Earthquake Research in China, 2012, 28(2): 133-143 DOI:10.3969/j.issn.1001-4683.2012.02.003)
(  0) 0) |
2. Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, CEA, 29 Xuefu Road, Harbin 150080, China
 2019, Vol. 39
2019, Vol. 39


