2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077;
3. 新疆维吾尔自治区地震局,乌鲁木齐市科学二街338号,830011
流动重力测量是地震监测的重要手段之一,它包括基准点上的绝对重力测量以及联测点间的相对重力联测。相对重力联测具有机动灵活、省时省力、经济成本低等优点,能快速获取地震重点监视区的区域重力场变化,近年来在强震危险性研究中发挥了重要作用[1-4]。
相对重力联测的目的是获得相邻测点间的重力值之差。目前,加拿大Scintrex公司生产的CG-5相对重力仪凭借其测量精度高、读数分辨率高以及自动化程度高等优点,已经成为世界上使用最广泛的相对重力仪[5-6]。由于CG-5相对重力仪的读数并不是重力值,为了将重力仪读数转换为重力值,需要事先获得仪器的格值函数,并按照式(1)进行格值转换计算获得测点的相对重力值。
| $ g = \sum\limits_{k = 1}^n {{E_k}{z^k}} $ | (1) |
式中,g为测点相对重力值,z为仪器读数,Ek为仪器的格值系数,k为阶数,一般只考虑到1次项,即n=1[7],因此,通常所说的格值系数即为一次项格值系数,在基线场标定及实测数据处理中只考虑仪器的一次项格值系数。
相对重力仪的格值函数会随时间发生变化,从而容易在数据处理及重力场变化的研究中引入虚假信息[8-9]。《地震重力测量规范》规定,相对重力测量应该考虑格值函数系数的误差,每隔3~5 a使用重力长基线或短基线对重力仪的格值系数进行标定[10]。由于相对重力仪的标定工作成本较高、投入人力物力较多、耗时较长,长基线的标定周期一般都在3 a以上,而区域地震重力测量周期一般为0.5~1 a,相对重力仪格值系数的基线标定工作无法满足实际测量需求。为减弱相对重力仪格值系数误差对数据处理结果的影响,一般采用两种方法对重力仪格值系数进行检测与校正:1)利用实测资料中分布均匀、相互之间段差较大的几个绝对重力点对重力仪格值系数进行标定,获得最适合该观测资料的格值系数;2)利用相邻两期观测结果中测点间重力段差的变化检测重力仪格值系数的变化[11-12]。
南天山重力测网于2013-09改造完成(图 1)。其中,2015~2016年4期流动重力观测数据均采用编号为509和511的CG-5相对重力仪,在此期间未对两台仪器进行格值系数标定。基于此,本文利用测网内的3个绝对重力点对格值系数进行实测标定,并比较实测数据标定前后格值系数的变化以及格值系数变化对数据处理结果的影响。
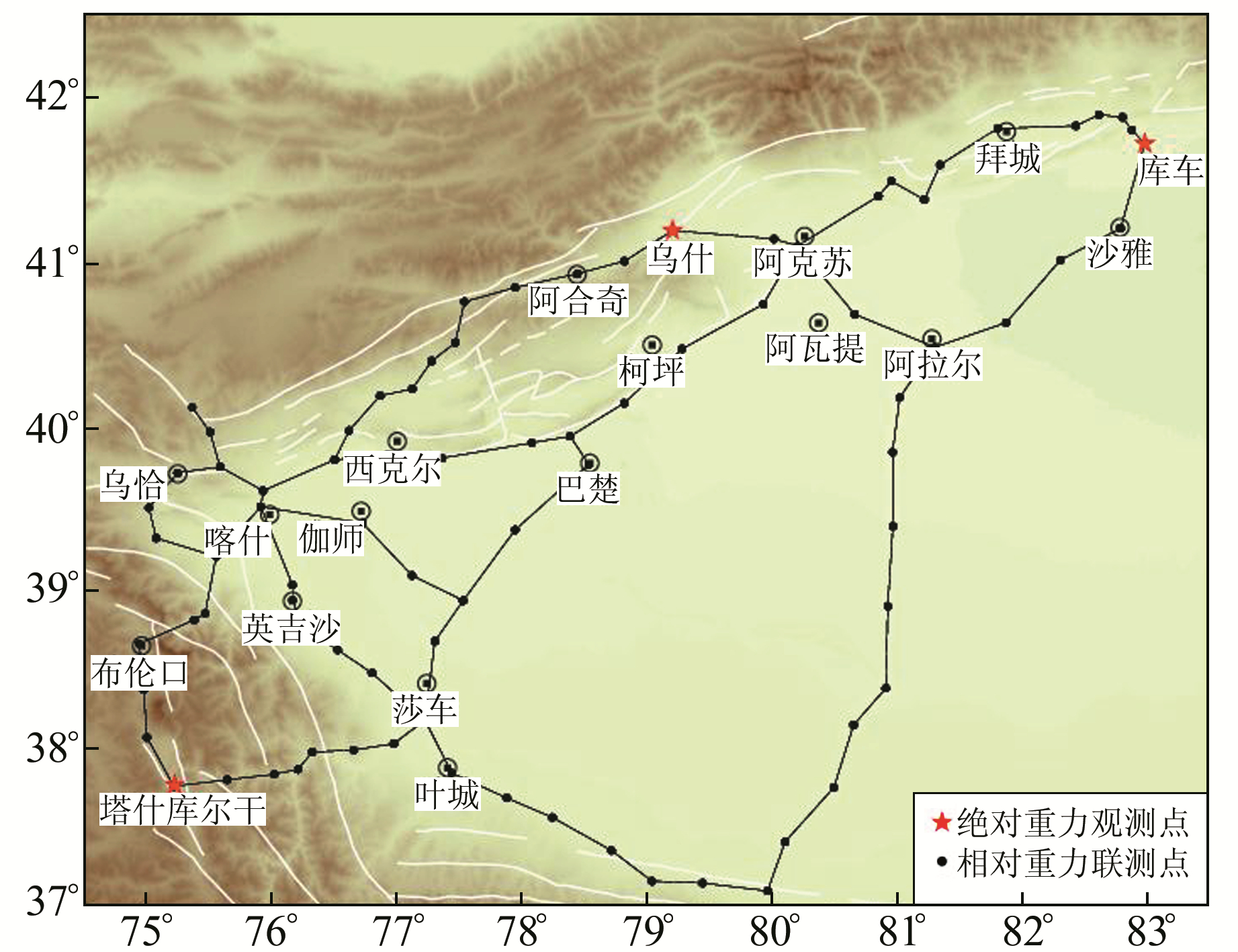
|
图 1 南天山重力测网路线 Fig. 1 Gravity monitoring network of southern Tianshan |
南天山重力测网2015~2016年4期观测数据的观测时间分别是2015-04、2015-08、2016-04和2016-08,所用的仪器格值系数分别是C509:1.000 000,C511:1.000 188。测网内的3个绝对重力点为乌什、塔什库尔干和库车,其最大重力段差达960 mGal,基本覆盖了整个测区的量程,可以作为仪器格值系数标定的控制点。但绝对重力测量周期过长,其相近的两期观测分别在2013-08与2016-04,由于南天山地区气候干燥,测点重力值受季节性变化影响较小,且两期重力变化较小,3个测点的重力变化分别为-9 μGal、-13 μGal、-2 μGal。因此,利用这两期的绝对重力值进行内插,计算得到各期相对重力观测时段内3个绝对重力点的重力值作为各期的平差基准。
以3个绝对重力点为基准,以给定的仪器格值系数为先验值,采用流动重力平差软件LGADJ[13]分别对4期观测数据进行平差计算,得到实测标定后的格值系数(表 1)。标定前后两台仪器的格值系数变化较大,从4期标定结果来看,前2期变化较大,后2期格值系数基本不变,说明CG-5重力仪在使用过程中比投入使用初期更加稳定。标定前后两台仪器的格值系数最大变化均在0.000 26左右,测网内最大的段差值为251 mGal,格值系数变化将会引入65 μGal的误差,严重影响了整网平差结果的可靠性。
|
|
表 1 标定前后相对重力仪的格值系数 Tab. 1 Scale factor coefficient of gravimeter before and after calibration |
为比较格值系数对数据处理结果的影响,利用表 1中标定前后的格值系数,以测网内3个绝对重力点为统一起算基准分别对4期观测数据进行平差计算,在先验中误差相同的情况下,对标定前后的后验中误差及剩余残差分布分别进行对比,见表 2与图 2。可以看出,由于第一期标定前后格值系数变化不大,其平差精度及剩余残差均无明显差别。而后3期标定后的整网平差精度明显高于标定前的平差精度,且随着格值系数变化的增大,标定前后平差精度的差异也越来越大。由剩余残差分布对比图同样可以看出,标定后的剩余残差值相对较小、残差分布紧凑,更符合正态分布,表明实测标定后的格值系数更适合该重力测网,标定后的平差精度更可靠。
|
|
表 2 标定前后测网的平差精度 Tab. 2 Adjustment precision of gravity network before and after calibration |
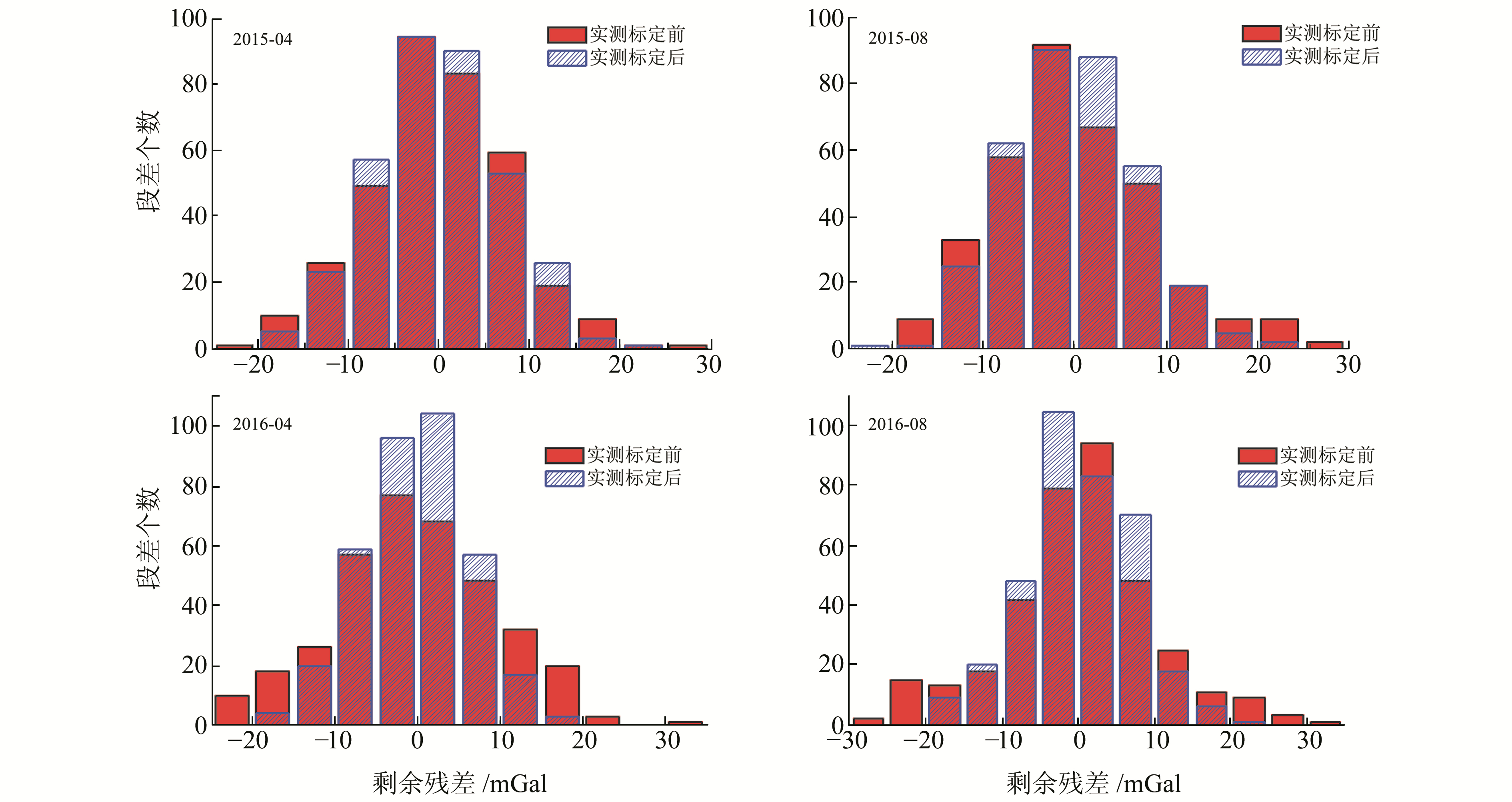
|
图 2 实测标定前后剩余残差分布 Fig. 2 Residual distribution of adjustment before and after calibration |
格值系数误差直接影响到每期的平差计算结果,从而在各期之间的重力场变化结果中会引入虚假信息。为进一步分析重力仪格值系数对重力场变化的影响,本文对格值系数实测标定前后获取的差分重力场变化及累积变化进行对比分析(图 3~6)。

|
图 3 标定前后重力场变化(2015-04~2015-08) Fig. 3 Gravity change before and after calibration(2015-04-2015-08) |

|
图 4 标定前后重力场变化(2015-08~2016-04) Fig. 4 Gravity change before and after calibration(2015-08-2016-04) |
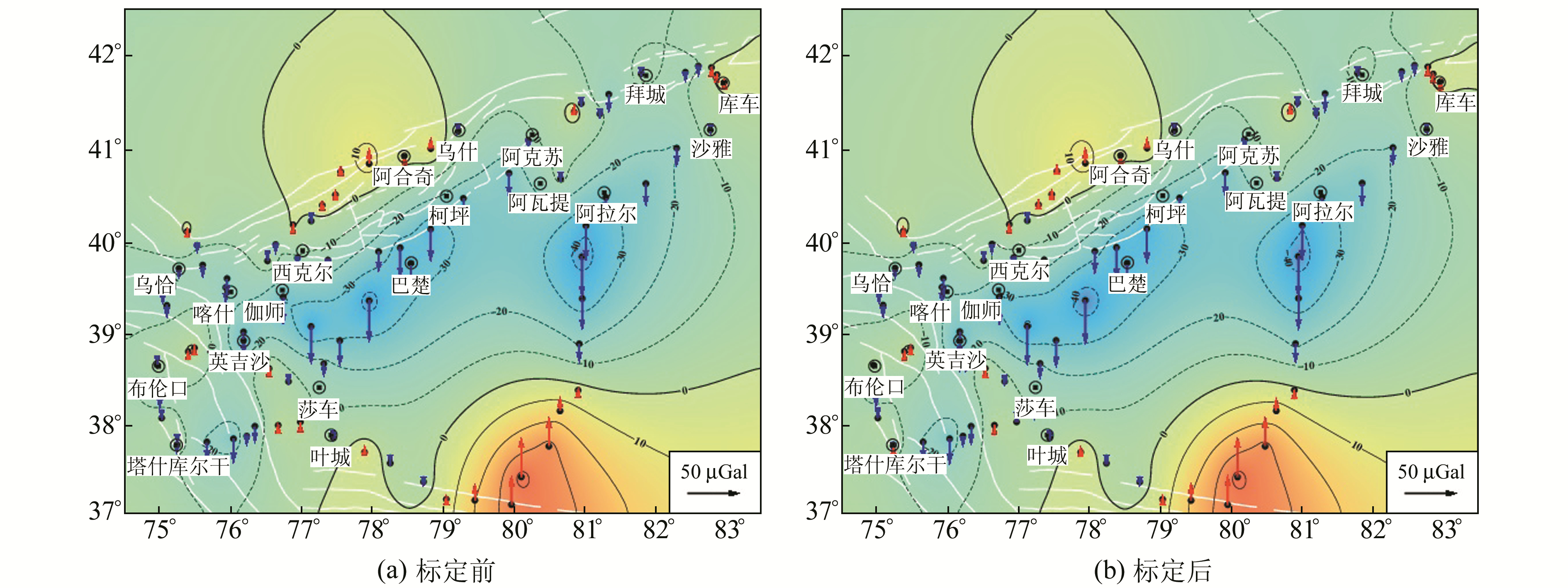
|
图 5 标定前后重力场变化(2016-04~2016-08) Fig. 5 Gravity change before and after calibration(2016-04-2016-08) |

|
图 6 标定前后累积重力场变化(2015-04~2016-08) Fig. 6 Gravity change before and after calibration(2015-04-2016-08) |
由差分重力变化对比图可以看出,对于2015-04~2015-08,标定前后重力变化趋势基本一致,但标定后重力变化量级明显减小,最大异常重力变化由标定前的110 μGal减小到90 μGal,南部正重力变化区域的最大值由标定前的90 μGal减小到40 μGal;对于2015-08~2016-04,标定前后重力变化量级差别不大,但重力变化趋势变化明显,标定后的负重力变化区域明显减小,且在巴楚-伽师附近形成了一个40 μGal左右的显著正重力变化区域;对于2016-04~2016-08,标定前后重力变化趋势及变化量级都基本一致,这是由于后两期观测过程中,仪器逐渐趋于稳定,格值系数基本不变,因此,使用原始格值系数与标定后的格值系数对两期的重力变化影响很小。由图 6 2015-04~2016-08的累积重力变化对比图可以看出,标定前后重力变化趋势差异非常显著,主要是由于两期仪器格值系数实际变化较大,其变化量分别为0.000 155和0.000 207,利用原始格值系数,假设两期观测期间仪器格值系数不变化会引入较大的系统误差。
由此分析,基线场的标定值不符合南天山测网的实际需求,且重力仪格值系数随时间发生变化,格值系数误差使得整网平差计算过程中引入系统误差,从而导致获取的重力场变化存在虚假信息,影响重力异常的识别及地震前兆异常的判定。
3 结语本文基于南天山重力测网2015~2016年的4期流动重力观测资料,以测区内3个绝对重力点作为平差的控制基准,分别在4个时段内对两台CG-5重力仪进行实测标定发现,实测标定的格值系数与基线场的标定结果差异较大,且随着使用时间的增加,仪器逐渐趋于稳定。利用标定前后的格值系数重新对各期数据进行平差计算,并对标定前后结果进行对比分析,结果表明,标定后的格值系数显著提高了平差精度,剩余残差明显减小,获取的重力场变化量级也明显减小。这充分说明实测标定后的格值系数更加适合南天山的测量需求,格值系数的实测标定有利于减弱格值系数误差带来的虚假信息。
目前地震系统使用CG-5重力仪较多,该仪器由于零漂较大,在同一测点同一型号的CG-5重力仪每年的读数值会有近100 mGal的变化,由于读数值的改变可能会影响到仪器格值标定时的读数范围,导致有些仪器的格值系数改变。本文讨论的两台CG-5重力仪格值系数每期观测变化较大可能是由以下两个原因引起:一是CG-5重力仪格值系数随观测时间不同发生变化;二是测区每期的读数范围不同程度地发生变化。这也是与传统的LCR-G型重力仪格值系数标定的主要区别。因此,利用CG-5型重力仪进行相对重力测量时,应尽量利用测区的准同期观测的绝对值,利用实测资料重新标定仪器的一次项,以获得真实可靠的重力变化信息,这有利于我们进一步识别重力异常与提取前兆异常信息,对利用重力观测资料进行强震危险性判定具有重要的实际意义。
| [1] |
Zhu Y Z, Zhan F B, Zhou J C, et al. Gravity Measurements and Their Variations before the 2008 Wenchuan Earthquake[J]. Bulletin of the Seismological Society of America, 2010, 100(5B): 2815-2824 DOI:10.1785/0120100081
(  0) 0) |
| [2] |
祝意青, 刘芳, 李铁明, 等. 川滇地区重力场动态变化及其强震危险含义[J]. 地球物理学报, 2015, 58(11): 4187-4196 (Zhu Yiqing, Liu Fang, Li Tieming, et al. Dynamic Variation of the Gravity Field in the Sichuan-Yunnan Region and Its Implication for Seismic Risk[J]. Chinese J Geophys, 2015, 58(11): 4187-4196)
(  0) 0) |
| [3] |
祝意青, 闻学泽, 孙和平, 等. 2013年四川芦山MS7.0地震前的重力变化[J]. 地球物理学报, 2013, 56(6): 1887-1894 (Zhu Yiqing, Wen Xueze, Sun Heping, et al. Gravity Changes before the Lushan, Sichuan, Ms=7.0 Earthquake of 2013[J]. Chinese J Geophys, 2013, 56(6): 1887-1894)
(  0) 0) |
| [4] |
王同庆, 陈石, 梁伟锋, 等. 2016年门源Ms6.4地震前的区域重力场变化与定量参数分析[J]. 地震地质, 2018, 40(2): 349-360 (Wang Tongqing, Chen Shi, Liang Weifeng, et al. The Variation of Regional Gravity Field and Quantitative Parameter Analysis before 2016 Menyuan Ms6.4 Earthquake[J]. Seismology and Geology, 2018, 40(2): 349-360 DOI:10.3969/j.issn.0253-4967.2018.02.005)
(  0) 0) |
| [5] |
邢乐林, 李辉, 夏正超, 等. CG-5重力仪零漂特性研究[J]. 地震学报, 2010, 32(3): 369-373 (Xing Lelin, Li Hui, Xia Zhengchao, et al. Study on Zero Drift Characteristics of CG-5 Gravimeter[J]. Acta Seismologica Sinica, 2010, 32(3): 369-373 DOI:10.3969/j.issn.0253-3782.2010.03.013)
(  0) 0) |
| [6] |
汪健, 孙少安, 邢乐林, 等. CG-5重力仪的漂移特征[J]. 大地测量与地球动力学, 2016, 36(6): 556-559 (Wang Jian, Sun Shaoan, Xing Lelin, et al. Drift Characteristics of CG-5 Gravimeter[J]. Journal of Geodesy and Geodynamics, 2016, 36(6): 556-559)
(  0) 0) |
| [7] |
刘乃苓, 江志恒. 拉科斯特重力仪中长周期格值标定因子的选择[J]. 地壳形变与地震, 1991, 11(1): 65-74 (Liu Nailing, Jiang Zhiheng. On the Choice of the Scale Function Factors of LCR Gravimeter[J]. Crustal Deformation and Earthquake, 1991, 11(1): 65-74)
(  0) 0) |
| [8] |
郝洪涛, 李辉, 孙和平, 等. CG-5重力仪零漂改正及格值系数检测应用研究[J]. 武汉大学学报:信息科学版, 2016, 41(9): 1265-1271 (Hao Hongtao, Li Hui, Sun Heping, et al. Application of Zero Drift Correct and Detection of Scale Parameters of CG-5 Gravimeter[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1265-1271)
(  0) 0) |
| [9] |
冯建林, 檀玉娟, 秦建增, 等. CG-5重力仪一次项格值系数对宁夏重力场变化的影响[J]. 大地测量与地球动力学, 2017, 37(3): 319-322 (Feng Jianlin, Tan Yujuan, Qin Jianzeng, et al. The Effect of One Degree Term of Chromatic Polynomial of CG-5 Gravimeter on Gravity Change in Ningxia Area[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 319-322)
(  0) 0) |
| [10] |
国家地震局.地震重力测量规范[S].北京: 地震出版社, 1997 (State Seismological Bureau. Seismological Gravimetric Standard[S]. Beijing: Seismological Press, 1997)
(  0) 0) |
| [11] |
郝洪涛, 李辉, 刘子维, 等. 基于重力差方法检测重力仪一次项格值系数变化[J]. 大地测量与地球动力学, 2011, 31(1): 87-90 (Hao Hongtao, Li Hui, Liu Ziwei, et al. Study on Change of Scale Parameters in Linear Term of Gravimeter with Gravity Difference Method[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 87-90)
(  0) 0) |
| [12] |
梁伟锋, 刘芳, 祝意青, 等. 重力仪一次项系数对重力场动态变化的影响研究[J]. 大地测量与地球动力学, 2015, 35(5): 882-886 (Liang Weifeng, Liu Fang, Zhu Yiqing, et al. Research on the Effect of One Degree Term of Chromatic Polynomial of Gravimeter on Gravity on Dynamic Change[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 882-886)
(  0) 0) |
| [13] |
刘绍府, 刘冬至, 李辉. 高精度重力测量平差及其软件[J]. 地震, 1991(4): 57-66 (Liu Shaofu, Liu Dongzhi, Li Hui. Adjustment of High Precision Gravity Measurements and Its Software[J]. Earthquake, 1991(4): 57-66)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
3. Earthquake Agency of Xinjiang Uyghur Autonomous Region, 338 Second Kexue Street, Urumqi 830011, China
 2019, Vol. 39
2019, Vol. 39

