陆地总水储量变化(total water storage change,TWSC)是水文循环的一个重要组成部分,2002-03发射的GRACE重力卫星为大尺度范围的水质量变化提供了足够精确的观测手段,其数据可以作为TWSC的一个合理且有效的估计值[1]。水旱灾害等极端气候事件的发生,会导致流域内TWSC出现异常变化现象,因此,研究TWSC的异常变化,便可以对水旱灾害进行定量分析。相关研究表明,极端水旱灾害在TWSC变化中表现较为明显[2]。
ENSO是热带海洋和大气的一种热力-动力异常的自然现象,会通过影响季风环流从而对降雨量和气温造成影响,使得正常的气候格局遭到破坏,引发极端水旱灾害等极端气候事件[3]。
亚马孙平原(50°~70°W,10°S~0°)位于南美洲北部,面积达560万km2,是世界上面积最大的冲积平原和赤道多雨区,受到ENSO的影响十分显著。相关研究表明[4],厄尔尼诺现象对亚马孙平原的影响尤为明显,具体表现为厄尔尼诺现象会明显减弱亚马孙流域的降雨量,导致干旱发生。
自2010年以来,在亚马孙平原发生的数次水旱灾害之中,2010年和2016年发生的两起旱灾格外引人关注。其中,2016年是亚马孙流域有史以来降雨量最少的一年,但是对该年发生的旱灾情况研究却相对较少。
因此,本文将2016年旱灾作为重点分析对象。对照灾害发生时间发现,2010年和2016年两次严重旱灾均发生在厄尔尼诺年。因此,本文将从研究亚马孙平原TWSC和ENSO指数之间的关系入手,结合降雨量、径流量等传统水文数据,探讨这两次旱灾和ENSO之间的关系。
1 数据与方法 1.1 GRACE反演水储量变化本文采用美国德克萨斯大学空间研究中心(CSR)提供的GRACE RL05月时变重力场数据,该数据的形式是球谐系数,最高为60阶[5],时间跨度为15 a(2002-08~2017-06),异常重力场通过扣除2005~2010年共6 a的平均时变重力场得到。由于大气、海洋潮汐、固体潮以及极潮等影响在GRACE卫星数据解算过程中已经由先验模型扣除[6],因此陆地上的时变重力场主要反映的是TWSC在季节尺度和年际尺度上的变化,以及其他未经模型化的地球物理信号(如冰后回弹等)。
GRACE时变重力场在实际运用之前需要先进行空间滤波平滑处理。GRACE TVG在解算过程中会出现两个问题:其一是会出现严重的南北条带误差,其二是高阶项和高次项中存在较严重的误差。为抑制高阶和高次项误差,本文采用非各向同性的Fan滤波对时变重力场进行平滑处理,滤波半径为250 km。同时还使用去相关性滤波方法,利用3次多项式拟合对8次及以上的球谐系数进行处理以平滑条带误差。除此之外,还利用卫星激光测距得到的高精度的C20项代替GRACE时变重力场模型C20项,用Swenson等[7]计算的1阶项取代GRACE时变重力场模型1阶项。经过以上处理之后,便可得到利用等效水高表示的TWSC数据。
由GRACE时变重力场球谐系数残差(ΔClm、ΔSlm)计算TWSC,并以等效水高的形式表示为:
| $ \begin{array}{l} {\rm{TWSC}}\left( {\theta, \lambda } \right) = \frac{{r{\rho _a}}}{{3{\rho _w}}}\mathop \sum \limits_{l = 0}^{60} \mathop \sum \limits_{m = 0}^l {W_{lm}}{{\bar P}_{lm}}\left( {{\rm{cos}}\theta } \right) \cdot \\ \;\;\;\;\;\frac{{2l + 1}}{{{k_l} + 1}}\left( {\mathit{\Delta }{{\bar C}_{lm}}{\rm{cos}}m\lambda + \mathit{\Delta }{{\bar S}_{lm}}{\rm{sin}}m\lambda } \right) \end{array} $ | (1) |
其中,θ为余纬,λ为经度,r为地球半径(6 378 136.46 m),ρw为淡水密度(1 000 kg/m3),ρa为地球的平均密度(5 517 kg/m3),Wlm为空间滤波因子,kl为负荷勒夫数,Plm(cosθ)为完全规格化的缔合勒让德多项式。
由于GRACE重力数据反演得到的陆地水储量变化是空间滤波的结果,存在泄漏误差,信号幅度会受到减弱,空间分辨率也会受到影响。因此,本文采用尺度因子[1]对GRACE数据进行重建,提高GRACE时变重力场的分辨能力。
经过上述处理,可得到2009-07~2017-06期间共108个月(其中12个月份存在数据缺失)全球1°×1°月平均质量变化格网数据。以纬度的余弦值为各格网的权重,根据亚马孙平原轮廓对区域内格网数据进行加权平均,便可得到该区域的平均水储量变化:
| $ {\rm{TWS}}{{\rm{C}}_{_{{\rm{basin}}}}}{\rm{ = }}\frac{{\sum\limits_{i = 1}^{\rm{N}} {{\rm{TWSC}}({\theta _i}, {\lambda _i}) \cdot {\rm{cos}}{\theta _i}} }}{{\sum\limits_{i = 1}^N {{\rm{cos}}{\theta _i}} }} $ | (2) |
受到GRACE自身条件的限制,GRACE TWSC序列中有部分月份缺失了数据,对12个数据缺失的月份,本文利用奇异谱分析方法(singular spectrum analysis, SSA)进行插值计算。
因ENSO一般表现为年际周期特征,为保证TWSC与ENSO指数相关性分析中信号的一致性,需在TWSC序列中移去趋势变化和季节性周期变化信号,将移去趋势项和季节周期项的TWSC称为TWSC异常(TWSC anomaly,TWSA)。如今常用的计算TWSA的方法是通过最小二乘拟合的方式拟合并去除TWSC中的线性趋势项和周期项,而TWSC一般情况下并不是平稳的线性变化趋势,因此,当TWSC为非线性趋势变化时,该方法会导致一定的误差。SSA方法在提取趋势信号时,无须事先假设趋势项的形式,可以最大限度上避免周期项和其他异常变化项的影响,有效提取非线性趋势信号。因此,本文采用SSA方法来提取亚马孙平原地区TWSC的趋势项,然后使用最小二乘拟合对周期为1 a和0.5 a的季节周期项进行拟合并扣除,以得到较为可靠的TWSA信号。
1.2 PDSI指数、水文模型和ENSO指数为验证TWSA和极端水旱灾害之间的相关性,本文选用帕尔默干旱指数(Palmer drought severity index,PDSI)作为参考。该指数是一个常用的干旱指标,基于土壤湿度的供需模型计算得到。PDSI为正数表示湿润程度,负数表示干燥程度,当某地区PDSI<-1.00时,表明该地区发生了干旱; 当PDSI<-2.00时,说明该地区旱情较为严重[8]。
本文使用的气象水文数据来自于全球陆地资料同化系统(global land data assimilation systems, GLDAS)[9]。该模型由美国宇航局(NASA)哥达空间飞行中心和美国国家环境预测中心共同构建,同时使用地面-空间观测值和模拟观测值对地面组分(如土壤湿度、温度等)进行估计。该数据有4个版本:Noah、Mosaic、VIC和CLM,本文使用Noah版本[10],其时间跨度为1979年至今,时间分辨率为月。本文选取的时间跨度为2009-07~2017-06共108个月,选取的数据包括等效雪量、土壤水分蒸发蒸腾损失总量(evapotranspiration,ET)、降雨量和地表径流量数据。GLDAS数据在使用前应采取和GRACE数据相同的处理方式,包括球谐展开并截止至60阶、利用Fan滤波进行空间平滑以及利用尺度因子对信号进行恢复和重建,最终得到1°×1°的格网数据。在平滑过程中,无需利用去相关性滤波进行处理。
本文采用多源ENSO指数(multivariate ENSO index, MEI)来研究ENSO,该指数通过海温、径向风、纬向风、海平面气压、海平面附近温度以及天空量共6个参数联立计算得到,是监测ENSO现象最为全面的指数,当MEI为正值时对应厄尔尼诺现象,为负值时对应拉尼娜现象。
2 计算结果与分析 2.1 MEI和亚马孙平原TWSA的相关性和时延性考虑到ENSO事件的年际周期特性,应当对TWSA使用滑动窗口进行平均处理,去除TWSA中的高频项。研究使用宽度为13个月的滑动平均窗口,受到该滤波窗口的限制,研究时间段缩短为2010-01~2016-12。首先,为了验证亚马孙平原TWSA可以有效反映出亚马孙平原的水旱灾害情况,将TWSA和PDSI分别进行滤波平滑处理,研究其相关性。相关性研究表明,亚马孙平原TWSA和PDSI之间的皮尔逊相关系数达到了0.75,通过置信水平为95%的相关性检验,说明两者呈显著正相关关系。图 1显示,在研究时间段中,2010年旱灾、2016年旱灾的PDSI指数均小于-2.00,属于严重旱灾;2011年出现的洪灾PDSI指数约为1.55,属于一般性的洪灾,不包含在极端水旱灾害的范围之中。在用虚线方框标出的2010年和2016年两次旱灾中,TWSA和PDSI均处于明显谷值,说明这两次旱灾在TWSA中均得到了有效反映。因此可以认为,亚马孙平原受到水旱灾害影响的状况可以通过TWSA得到有效反映。

|
图 1 经13个月滑动平均滤波平滑处理后亚马孙平原TWSA和PDSI、MEI之间的相关性(2010-01~2016-12) Fig. 1 The correlations between TWSA, PDSI and MEI in Amazon basin from January 2010 to December 2016 after applying the 13-month moving-average filter |
为进一步确定ENSO和两次旱灾之间的关系,对MEI和亚马孙平原TWSA之间的关系进行探讨。在对TWSA和MEI分别进行滤波平滑处理后,比较两者之间的相关性,并计算两者的相关系数,结果也汇总至图 1之中。考虑到MEI指数为正时对应的是厄尔厄尼诺现象,已有研究表明[4],厄尔尼诺现象在亚马孙平原上会导致降雨量下降,而该地区降雨量和TWSC之间高度正相关,因此MEI和亚马孙平原TWSA之间应当呈负相关关系。为了能更好地表述两者之间的相关性,在图 1中将MEI乘以-1,并将2010年旱灾和2016年旱灾的相关时间段用虚线方框标示出来。
计算结果显示,MEI与亚马孙平原TWSA的皮尔逊相关系数为-0.37,通过了置信水平为95%的相关性检验,说明两者有明显的负相关关系。图 1显示,在亚马孙平原上,TWSA和MEI之间存在着一定的相位差,在2010年旱灾和2016年旱灾中,MEI均先于TWSA到达谷值;而在2011年,MEI也先于TWSA到达峰值点。因此,我们对MEI进行时延处理,寻找两者相关系数的最值,当在MEI中加入5个月的时间延迟时,两者相关系数达到最小值,为-0.59。这说明,ENSO事件会对亚马孙平原造成显著影响,该影响具有一定的时延性,以下称该时延为“ENSO-TWSA时延”,对于亚马孙平原而言,ENSO-TWSA时延为5个月,这和Phillips等[11]提出的时延一致。
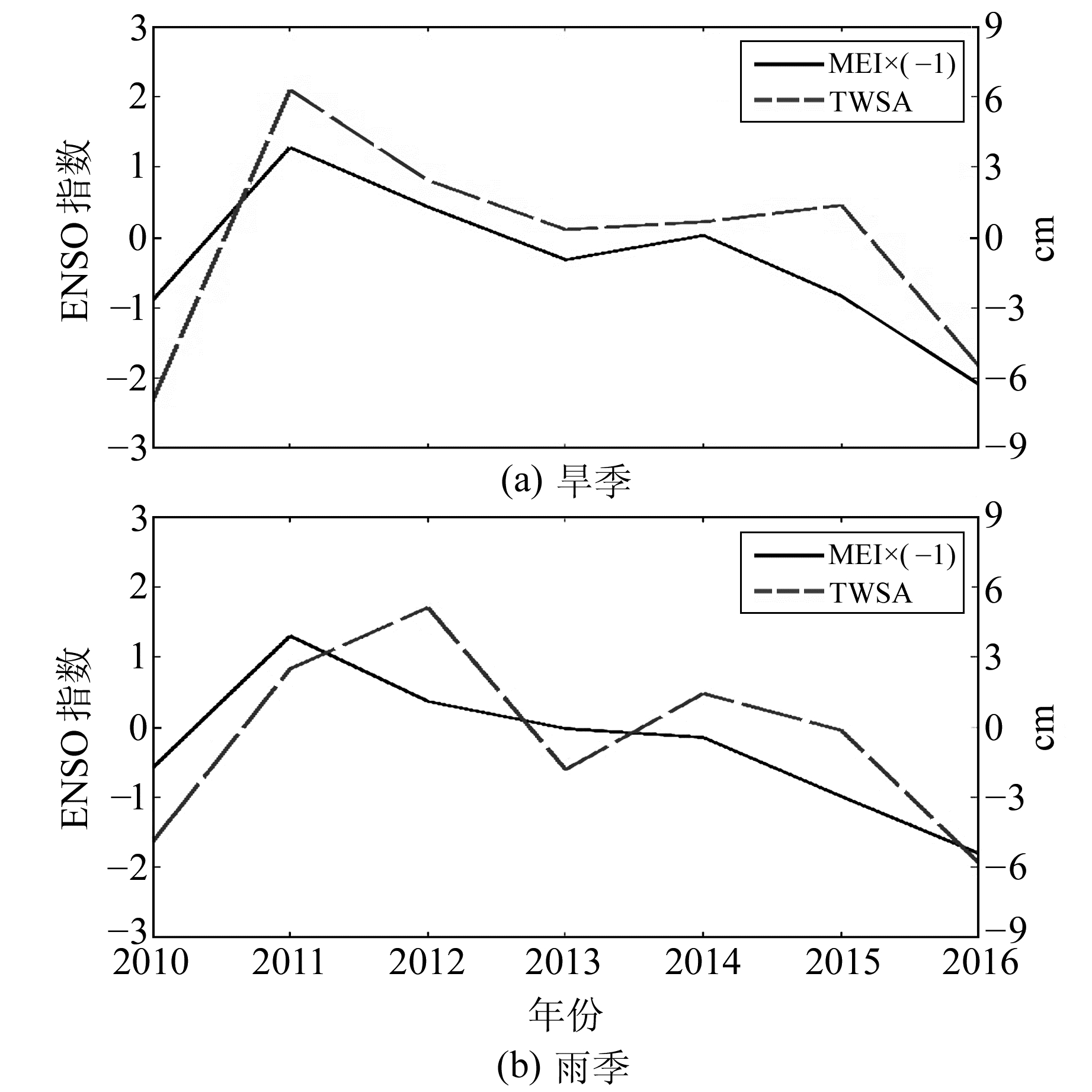
随后,分别计算MEI指数在旱季和雨季与TWSA之间的关系。根据季节特点,亚马孙平原的旱季为5~10月,雨季为11月~次年4月。把5~10月TWSA和MEI分别取平均,作为该年旱季的TWSA和MEI;把前一年11月、12月和该年1~4月TWSA和MEI分别取平均,作为该年雨季TWSA和MEI,并分别计算相关系数,计算结果如图 2所示。
|
图 2 2010~2016年亚马孙平原旱季及雨季TWSA和MEI之间的相关性 Fig. 2 The correlations between TWSA and MEI in Amazon basin during dry season as well as during rainy season from 2010 to 2016 |
计算结果显示,旱季时MEI和TWSA之间的相关系数为-0.85,通过置信水平为95%的相关性检验,两者呈明显的负相关关系。MEI越大,厄尔尼诺现象越严重,会导致TWSA越小,亚马孙平原旱情越严重。而在雨季时,两者相关系数为-0.13,呈微弱的负相关关系,这说明ENSO现象在雨季对亚马孙平原影响不大。
综上所述,MEI和亚马孙平原TWSA之间有明显的负相关关系,该关系存在着一定的时延性,当时延取5个月时,两者相关性达到最小值,为-0.59。这说明ENSO对亚马孙平原会产生明显的影响,具体表现为厄尔尼诺现象越强烈,TWSA越小,越容易发生旱灾;拉尼娜现象越强烈,TWSA越大,越容易发生洪涝灾害。从季节层面而言,MEI和TWSA在旱季时呈现明显的负相关关系,而在雨季时两者之间仅存在微弱的负相关关系,这说明ENSO主要在旱季时对亚马孙平原产生影响,随着ENSO事件的加强,亚马孙平原的旱情会加重;而在雨季时则基本不会产生影响。
2.2 ENSO和亚马孙平原极端水旱灾害的联系上述分析结果显示,ENSO和亚马孙平原TWSA之间存在着明显的相关性和时延特性,其中,旱季时亚马孙平原受到ENSO影响更为强烈。水文资料表明,2010年旱灾和2016年旱灾均发生于旱季,由此可以推断,这两次旱灾均应受到ENSO的明显影响。基于水量平衡方程,只有当降雨量、径流量和ET中的一个或多个发生变化时,TWSC才会发生变化[11],而相关研究表明,亚马孙平原的水旱灾害和ET相关性较小,因此本文选用了径流量(R)和降雨量(P)验证这一推断。
首先利用和前文类似的方法,结合最小二乘方法和SSA对P和R的趋势项和周期项进行拟合并去除,并利用13个月的滑动平均滤波对其分别进行平滑处理,得到P和R的异常(以下简称“P异常”和“R异常”);然后,将得到的ENSO-TWSA时延对MEI进行延迟处理,并分别计算延迟处理后MEI和P异常、R异常之间的相关系数;最后,为了使结果能得到更好的呈现,除了给MEI乘以-1之外,还将P异常和R异常分别乘以1.2和2,并将2010年旱灾和2016年年旱灾用虚线方框标出,得到图 3。

|
图 3 经13个月滑动平均滤波平滑处理和时延处理后亚马孙平原MEI、TWSA、P异常和R异常之间的相关性(2010-01~2016-12) Fig. 3 The correlations between MEI, TWSA, P anomaly and R anomaly in Amazon basin from January 2010 to December 2016 after applying the 13-month moving-average filter and the time lags |
计算结果显示,MEI和P异常、R异常之间的相关系数分别为-0.73和-0.70,均通过置信水平为95%的相关性检验,呈明显的负相关关系。图 3显示,在经过时延处理之后,MEI和TWSA之间的相位差得到消除。在2010年旱灾和2016年旱灾期间,TWSA、P异常和R异常分均出现明显谷值,MEI也出现明显谷值,说明MEI在此处出现明显峰值。P异常和R异常分的谷值表明,这两次旱灾的发生均是降雨量、径流量偏小所导致的;MEI出现明显峰值则表明,导致降雨量、径流量偏小的原因和厄尔尼诺现象有很大关联。研究表明,ENSO现象对亚马孙平原会产生很大影响,尤其是在厄尔尼诺现象发生时,会使得亚马孙平原降水、径流量都发生不同程度的减少,从而造成旱灾。
3 结语本文利用GRACE时变重力场反演2009-07~2017-06 TWSC序列,结合MEI指数和气象水文数据,分析亚马孙平原水储量变化与ENSO之间的关系,并重点分析2010年和2016年发生于该地区的两起极端旱灾和ENSO的联系。移去趋势和季节性周期信号后得到的亚马孙平原TWSA序列经过滑动平均处理后显示,其与该地区的PDSI之间具有较强的正相关性,说明TWSA可以较好地表述亚马孙平原的水旱灾害情况,尤其是旱灾情况;TWSA还和MEI指数之间具有较强的负相关性,说明ENSO事件会对亚马孙平原造成明显影响,当发生厄尔尼诺现象时,TWSA变小,容易发生旱灾,而当发生拉尼娜现象时,TWSA变大,容易发生洪涝灾害。此外,该影响还具有一定的时延性,时延为5个月。从季节层面而言,旱季时两者呈现明显的负相关关系,雨季时两者呈现微弱的负相关关系,这说明ENSO主要在旱季时影响亚马孙平原,具体表现为该地区的旱情会随着厄尔尼诺的加强而加强,在雨季时对亚马孙平原则几乎不会产生明显影响。
随后,本文研究气象水文数据和MEI指数的关系,并结合水量平衡方程,探讨ENSO现象和2010旱灾以及2016旱灾之间的联系。研究表明,MEI和P异常、R异常之间均存在着明显的负相关关系,在两次旱灾期间,亚马孙平原的TWSA、P异常和R异常分均出现了明显谷值,MEI则出现了明显峰值,这说明这两次旱灾和厄尔尼诺现象有明显关联,厄尔尼诺现象的发生与加强导致亚马孙平原的降雨量、径流量明显减少,从而使得TWSA减少,旱情加重。
| [1] |
Landerer F W, Swenson S C. Accuracy of Scaled GRACE Terrestrial Water Storage Estimates[J]. Water Resour, 2012, 48(4): 4531
(  0) 0) |
| [2] |
Long D, Scanlon B R, Longuevergne L, et al. GRACE Satellite Monitoring of Large Depletion in Water Storage in Response to the 2011 Drought in Texas[J]. Geophysical Research Letters, 2013, 40(13): 3395-3401 DOI:10.1002/grl.50655
(  0) 0) |
| [3] |
Ropelewski C F, Halpert M S. Global and Regional Scale Precipitation Patterns Associated with the El Niño/Southern Oscillation[J]. Monthly Weather Review, 1987, 115(8): 1606-1626 DOI:10.1175/1520-0493(1987)115<1606:GARSPP>2.0.CO;2
(  0) 0) |
| [4] |
Bookhagen B, Strecker M R. Modern Andean Rainfall Variation during ENSO Cycles and Its Impact on the Amazon Drainage Basin[A]// Amazonia: Landscape and Species Evolution: A Look into the Past[M]. Wiley-Blackwell Publishing Ltd, 2011
(  0) 0) |
| [5] |
Bettadpur S. Assessment of GRACE Mission Performance and the RL05 Gravity Fields[C]. Abstract G31C-02 Fall Meeting, AGU, San Francisco, 2012
(  0) 0) |
| [6] |
Bettadpur S. Gravity Recovery and Climate Experiment Level-2 Gravity Field Product User Handbook[M]. Cent For Space Res, Austin, Texas, 2007
(  0) 0) |
| [7] |
Swenson S, Chambers D, Wahr J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J]. Journal of Geophysical Research Atmospheres, 2008, 113(B8): 194-205
(  0) 0) |
| [8] |
Dai A G, Trenberth K E, Qian T T. A Global Data Set of Palmer Drought Severity Index for 1870–2002: Relationshipwith Soil Moisture and Effects of Surface Warming[J]. Journal of Hydrometeorology, 2004, 5(6): 1117-1130 DOI:10.1175/JHM-386.1
(  0) 0) |
| [9] |
Rodell M, Houser P R, Jambor U E A, et al. The Global Land Data Assimilation System[J]. Bulletin of the American Meteorological Society, 2004, 85(3): 381-394 DOI:10.1175/BAMS-85-3-381
(  0) 0) |
| [10] |
Ek M B, Mitchell K E, Lin Y, et al. Implementation of the Upgraded Noah Land-Surface Model in the NCEP Operational Mesoscale Eta Model[J]. J Geophys Res, 2003, 108: 8851 DOI:10.1029/2002JD003296
(  0) 0) |
| [11] |
Phillips T, Nerem R S, Fox-Kemper B, et al. The Influence of ENSO on Global Terrestrial Water Storage Using GRACE[J]. Geophysical Research Letters, 2012, 39(16): L16 705
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

