2. 中国测绘科学研究院,北京市莲花池西路28号,100830
现代大地测量和地球物理观测技术得到不断突破,超导重力仪的观测精度可达±0.1 μGal,甚长基线干涉测量(VLBI)、卫星激光测距(SLR)、全球定位系统(GPS)基线解算精度可达±0.1~±1 cm(10-8~10-9)量级[1]。要获得高精度的大地测量结果,必须进行严密的数据处理和严格的干扰信号剔除,而干扰信号中大气变化是主要干扰噪声。大气压周期性变化引起地面点地壳垂直形变可达±25 mm,对地面重力影响可达±20 μGal[2]。显然,对于高精度的大地测量,如参考框架的建立、基准点的确定,大气影响改正不可忽略,因此精确的大气负荷变化研究不仅可用于GPS基线解算和精密重力测量等其中的大气改正,而且对提高不连续观测站的观测精度也具有重要的实用价值[3]。
大气负荷影响的计算方法主要有负荷格林积分法和球谐函数法。负荷格林积分法是Farrell[4-5]基于Longman地球负荷理论,从理论上推出球对称地球在单位点质量负荷下的静态格林函数,解决其计算问题,即结合气压变化数据和格林函数的褶积积分,可以得到大气变化产生的位移、重力、倾向和应变效应。罗少聪等[1]利用弹性地球负荷理论和流体静力学平衡,计算大气压作用下地表位移重力和格林倾斜函数,表明大气效应弹性影响主要来自于远离台站的区域,引力项对重力影响的主要贡献来自于台站近区。许多学者[6-8]又根据Farrell理论给出应用球谐函数直接计算地表流体负荷(大气、海洋、陆地水、冰雪圈等)质量变化产生的负荷响应公式。张诗玉等[3]利用球谐系数方法研究大气负荷效应对GPS基准站的影响表明,大气负荷引起的地壳垂直形变可达20~30 mm,表现为明显的季节性变化。沈迎春等[9]比较上述两种计算方法的结果精度和运算速度表明,两种方法在数学本质上是一致的,计算精度和运算速度在相同分辨率下差异不大。
本文利用全球大气变化模型资料,结合研究区域内气象站实测气压变化数据,采用移去-恢复法计算新疆区域大气负荷变化对地壳形变和重力的影响,并分析其影响特征。
1 理论方法 1.1 基本理论和公式根据气压原理将全球大气模型转换为等效水高变化,地面一点的等效水高变化量Δhw(
| $ \begin{array}{l} \mathit{\Delta }{h_{\rm{w}}}(\varphi, \lambda ) = R\sum\limits_{n = 1}^N {\sum\limits_{m = 0}^n {\left[{\mathit{\Delta }C_{nm}^q{\rm{cos}}m\lambda + } \right.} } \\ \left. {\mathit{\Delta }S_{nm}^q{\rm{sin}}m\lambda } \right]{{\bar P}_{nm}}({\rm{sin}}\varphi ) \end{array} $ | (1) |
根据地球负荷形变和重力场理论,地面等效水高变化引起一点的大地高(垂直位移形变)负荷变化量为:
| $ \begin{array}{l} \;\;\mathit{\Delta }r(\varphi, \lambda ) =-3\frac{{\rho {}_{\rm{w}}}}{{\rho {}_{\rm{e}}}}\frac{{GM}}{{R2}}\sum\limits_{n = 1}^N {\frac{{{{h'}_n}}}{{2n + 1}} \cdot } \\ \sum\limits_{m = 0}^n {(\mathit{\Delta }C_{nm}^q{\rm{cos}}m\lambda + \mathit{\Delta }S_{nm}^q{\rm{sin}}m\lambda )} {{\bar P}_{nm}}({\rm{sin}}\varphi ) \end{array} $ | (2) |
引起的地面重力变化为:
| $ \begin{array}{l} {g_t}(\varphi, \lambda ) =-3\frac{{\rho {}_{\rm{w}}}}{{\rho {}_{\rm{e}}}}\frac{{GM}}{{R2}}\sum\limits_{n = 1}^N {\frac{{n + 2{{h'}_n}-(n + 1){{k'}_n}}}{{2n + 1}} \cdot } \\ \;\;\;\;\;\;\;\sum\limits_{m = 0}^n {(\mathit{\Delta }C_{nm}^{\rm{q}}{\rm{cos}}m\lambda + \mathit{\Delta }S_{nm}^q{\rm{sin}}m\lambda )} {{\bar P}_{nm}}({\rm{sin}}\varphi ) \end{array} $ | (3) |
式(1)~(3)中,
同样,大气负荷引起的地面重力变化和地表大地高变化也可以用格林函数积分法进行计算。负荷格林函数积分通用公式为:
| $ \mathit{\Delta \Theta }\left( {\varphi, \lambda } \right) = G{\rho _{\rm{w}}}\mathop \int\!\!\!\int \limits_S^{} \frac{{{h_{\rm{w}}}\left( {\varphi ', \lambda '} \right)}}{L}G\left( \psi \right){\rm{d}}S $ | (4) |
式中,(
重力格林函数计算公式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{G^g}\left( {\varphi, \lambda } \right){\rm{ = }}\\ - \frac{\gamma }{M}\sum\limits_{n = 1}^\infty {\left[{n-(n + 1){{k'}_n} + 2{{h'}_n}} \right]{P_n}{\rm{cos}}(\psi )} \end{array} $ | (5) |
式中,Pn(·)为n阶勒让德函数。
大地高变化格林函数Gr为:
| $ {G^r}\left( {\varphi, \lambda } \right){\rm{ = }}\frac{R}{M}\sum\limits_{n = 1}^\infty {{{h'}_n}{P_n}{\rm{cos}}(\psi )} $ | (6) |
将式(6)代入式(4),得到计算任意点(
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Delta \Theta }\left( {\varphi, \lambda } \right) = \\ G{\rho _{\rm{w}}}\mathop \int\!\!\!\int \limits_S^{} \frac{{{h_{\rm{w}}}\left( {\varphi ', \lambda '} \right)}}{L}\frac{R}{M}\sum\limits_{n = 1}^\infty {{{h'}_n}{P_n}{\rm{cos}}(\psi )} {\rm{d}}S \end{array} $ | (7) |
移去-恢复方法广泛应用于拟合大地水准面和重力场研究[12]。采用移去-恢复法,可以发挥区域实测气压变化优势,显现区域差异,提高模型的区域适用性,准确表现区域负荷变化特征。在移去过程中,需要将式(7)进行改进,将式中的积分域S分成近区S0和远区S-S0,则近区的等效水高积分公式变为:
| $ \begin{array}{l} \mathit{\Delta \Theta }(\varphi, \lambda ){|_{{S_0}}} = G{\rho _{\rm{w}}}\mathop \int\!\!\!\int \limits_S^{} \frac{{{h_{\rm{w}}}\left( {\varphi ', \lambda '} \right)}}{L}\frac{R}{M} \cdot \\ \;\;\;\sum\limits_{n = 1}^\infty {{{h'}_n}{P_n}{\rm{cos}}(\psi )} {\rm{d}}S + \mathop \int\!\!\!\int \limits_{{S_0}}^{} {\rm{d}}{h_{\rm{w}}}G({\psi _0}){\rm{d}}S \end{array} $ | (8) |
式中,dhw=Δhw(
移去-恢复法主要流程为:
1) 将全球大气模型数据扣除基准值,转换为等效水高值,得到每月全球大气等效水高相对于基准值的变化量,根据球谐分析法展开为等效水高球谐系数。
2) 利用等效水高球谐系数计算气象站位置处的模型等效水高,将气象站气压值同样扣除基准值后转换为等效水高。移去球谐系数等效水高,得到气象站位置处模型与实测的差异,称之为残差等效水高。这一步称之为“移去”。
3) 将站点残差等效水高采用克里金插值法格网化[2],基于格林函数积分法计算残差等效水高对区域地壳形变和地面重力变化的影响。
4) 将全球大气等效水高球谐系数计算的地壳形变或地面重力变化与残差等效水高计算的地壳形变或地面重力变化相加,得到大气负荷的间接影响。这一步称之“恢复”。
5) 由于大气对地面重力变化的影响还包括负荷的直接影响,即大气负荷对重力变化的影响为间接影响与直接影响之和。
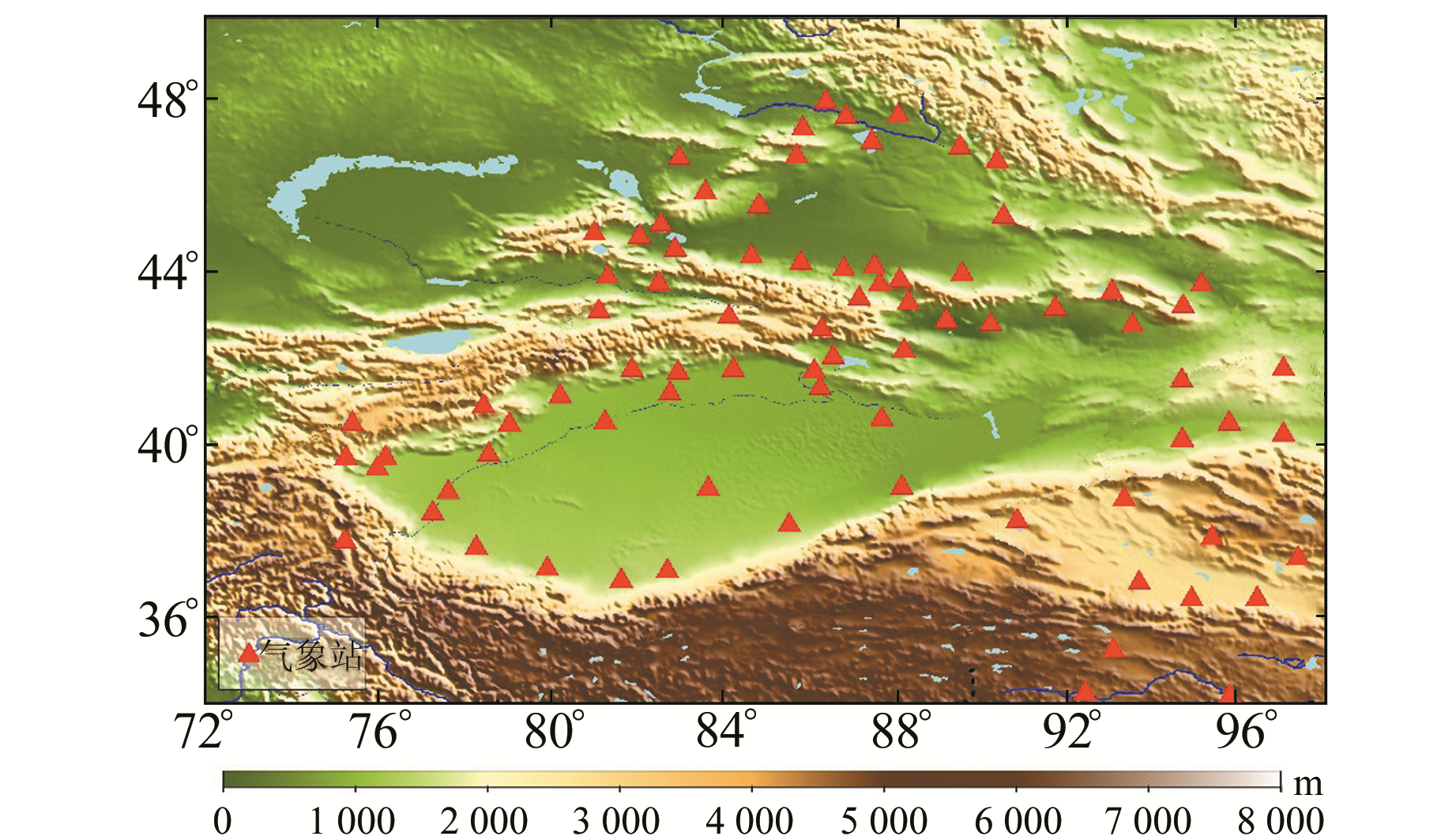
2 研究区域和数据处理 2.1 研究区域本文研究区及区域内气象站分布如图 1所示。
|
图 1 研究区域和气象站分布 Fig. 1 Distribution of meteorological stations in the studied area |
将下载自欧洲中期天气预报中心ECMWF(European centre for medium-range weather forecasts)的0.25°×0.25°月平均值全球大气模型数据扣除一个基准值,作为气压变化量[13]。
根据气压原理,按照1 hPa气压值等于10.197 2 mm等效水高的关系,将全球大气数据资料转换为相应的等效水高。根据式(1)将其展开为360阶球谐系数,并根据区域内已知的气象站点位置坐标求得每月等效水高,作为全球大气模型等效水高数据,在后续将进行“移除”操作。利用区域内0.25°×0.25°分辨率的坐标数据,根据式(2)求得区域内各点的垂直形变量。
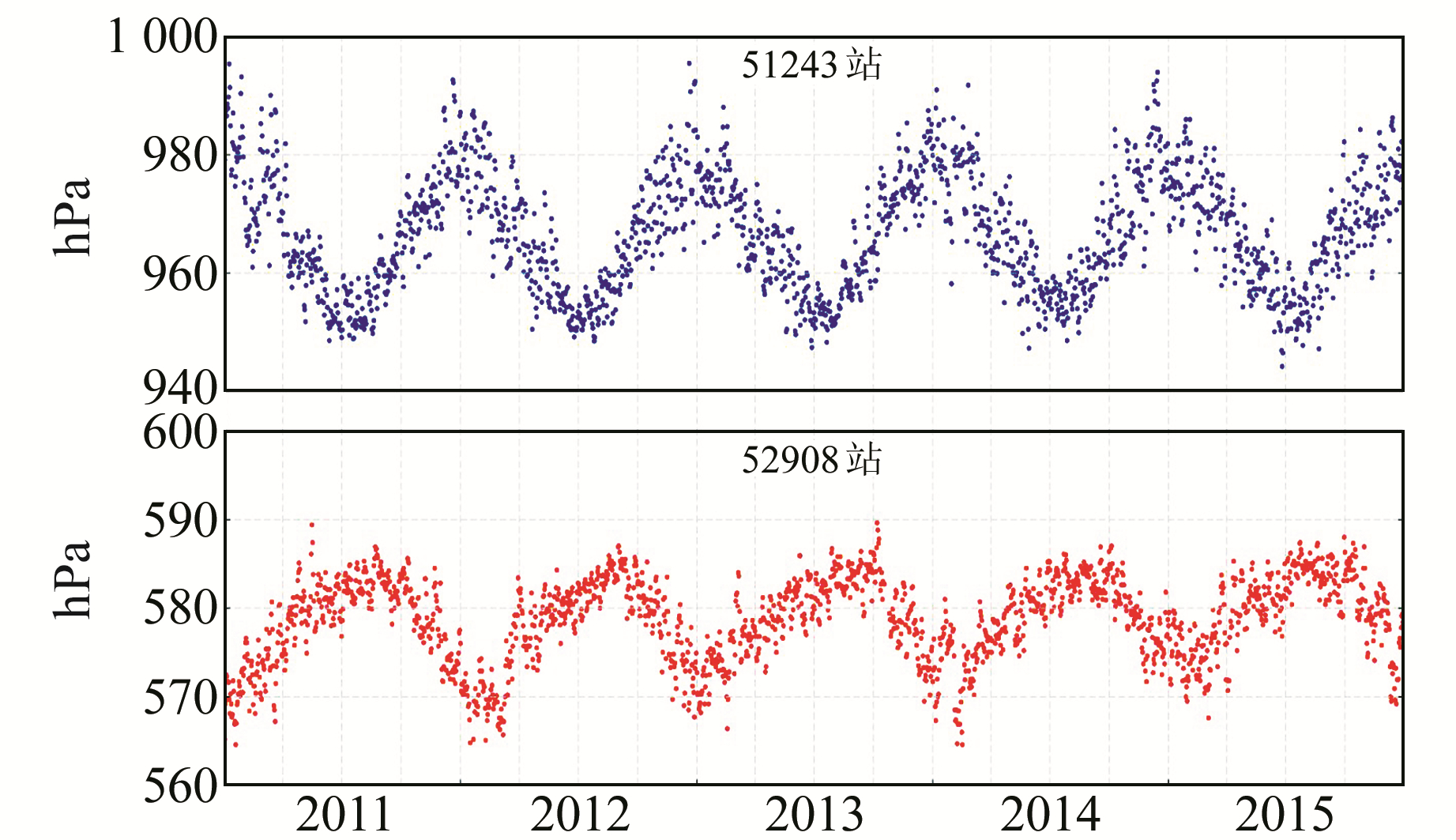
2.2.2 气象站观测气压数据处理气象站气压观测资料来自于国家气象科学数据共享服务平台网提供的中国地面气候资料日值数据集。通过将气象站观测数据剔除缺省值和粗差后绘图发现,该区域内低海拔气象站气压年变化表现为:一般区域夏季气压低、冬季气压高,如图 2中51243站海拔449.5 m;而位于昆仑山脉高海拔地区的气象站气压变化呈现夏季气压高、冬季气压低的反转现象,且年变化量较小,如图 2中52908站海拔4 612.2 m,呈现区域变化差异的复杂性。之后将气象站实测日值数据转换为月平均值,并扣除同一月份的基准值,根据气压原理将气压值转换为等效水高,作为区域实测气压值变化。减去全球大气等效水高球谐系数计算的等效水高,即移去模型等效水高值,得到的值称为残差等效水高,并采用surfer中的克里金插值法将残差等效水高进行区域格网化[2]。根据等效水高格林积分法(式(7))计算垂直形变的影响,高程数据采用等分辨率的SRTM数据。
|
图 2 气象站气压日值变化 Fig. 2 Variation of daily data of atmospheric pressure at the meteorological stations |
本文研究时间跨度为2011~2015年,在基准选择上根据研究时间跨度,选择2011-05的月平均值作为基准值扣除。将球谐系数计算的全球大气模型地壳形变与格林函数计算的残差等效水高相应的地壳形变相加,得到最终大气负荷对新疆区域地壳形变的总影响。
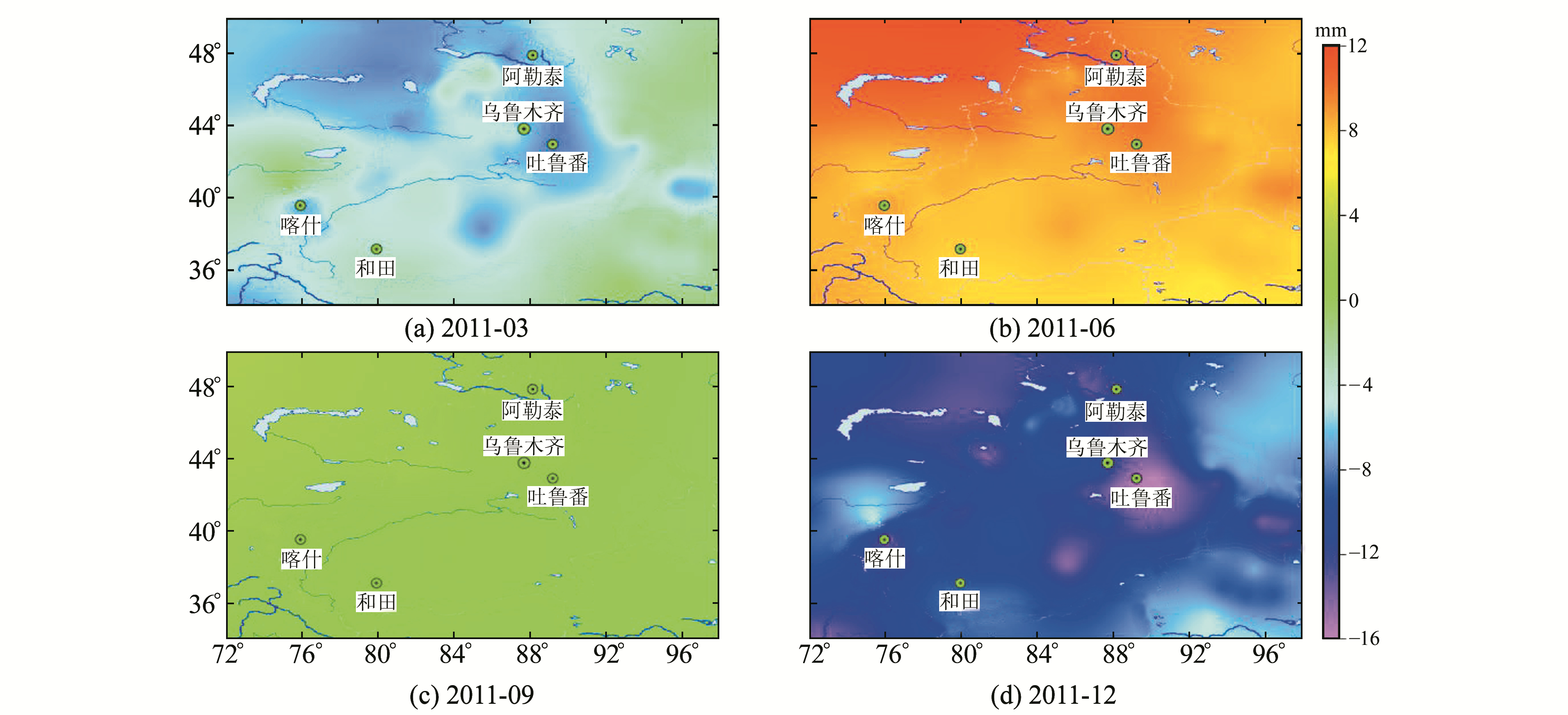
根据计算的大气负荷对地壳形变的影响,表现为明显的年周期变化。图 3和图 4为2011年和2013年中4个月的地壳垂直形变,由图可见,垂直形变最大年变化量出现在吐鲁番盆地,大约为25 mm,这与该地区气压年变化量较大相符。图 5和图 6为2012年和2014年中4个月的地壳水平形变变化情况,由图可见,水平形变量较小,在1 mm左右。
|
图 3 2011年大气负荷对地壳垂直形变的影响 Fig. 3 Effect of atmospheric load on vertical deformation of the crust in 2011 |

|
图 4 2013年大气负荷对地壳垂直形变的影响 Fig. 4 Effect of atmospheric load on vertical deformation of the crust in 2013 |

|
图 5 2012年大气负荷对地壳水平形变的影响 Fig. 5 Effect of atmospheric loading on horizontal deformation of the crust in 2012 |

|
图 6 2014年大气负荷对地壳水平形变的影响 Fig. 6 Effect of atmospheric load on horizontal deformation of the crust in 2014 |
大气负荷对地面重力的影响分为直接影响和间接影响,直接影响就是气压变化直接引起的重力变化;间接影响是指大气负荷变化导致的固体地球内部密度质量重新分布引起的重力变化[9],直接影响占主要部分。
采用大气导纳方法计算大气负荷对地面重力变化的影响,理论大气导纳值为-0.303 7 μGal/hPa[2],包含直接影响和间接影响。由全球大气模型中提取区域大气数据,扣除参考基准值,得到大气变化数据,然后乘以理论大气导纳值,得到区域大气负荷对地面重力的影响。2015-03、2015-06、2015-09、2015-12大气对地面重力的影响变化如图 7所示,由图可见,重力变化与气压值变化成反比,年变化幅度在10 μGal左右。

|
图 7 2015年大气负荷对地面重力的影响 Fig. 7 Effect of atmospheric load on ground gravity in 2015 |
为了全面了解大气负荷对新疆区域大地测量要素的影响,对其进行统计分析,如表 1所示。大气负荷对地壳形变和地面重力变化的影响具有年周期变化特征,通过统计其年变化幅度,了解其影响量级和变化规律。由表 1看出,大气负荷对垂直形变的影响最大为12.00 mm、最小为-17.97 mm,对水平影响较小(在1 mm以内);大气对地面重力的影响与大气变化具有明显的负相关性,年变化幅度在11.00 μGal以内。
|
|
表 1 大气负荷对大地测量要素影响统计 Tab. 1 Influence statistics of atmospheric load on geodetic factors |
本文采用移去-恢复法,将全球大气模型资料和气象站实测气压数据结合起来,利用球谐函数法和格林函数法,计算新疆区域的大气负荷月变化对区域地壳形变和地面重力的影响。结果表明,大气负荷影响具有明显的年周期变化特征,在新疆地区大气负荷对地壳垂直形变影响的年变化量超过20 mm,对水平形变影响的年变化量在1.2 mm以内;对地面重力的影响超过10 μGal,与区域气压变化量呈现正相关。
| [1] |
罗少聪, 孙和平, 徐建桥. 大气负荷引起的重力与位移变化理论计算的精度估计[J]. 测绘学报, 2001, 30(4): 309-315 (Luo Shaocong, Sun Heping, Xu Jianqiao. Theoretical Computation in the Precision Estimation of the Change in Gravity and Displacements Due to Atmospheric Loading[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 309-315 DOI:10.3321/j.issn:1001-1595.2001.04.007)
(  0) 0) |
| [2] |
罗少聪.大气负荷效应问题研究[D].武汉: 中国科学院测量与地球物理研究所, 2003 (Luo Shaocong. Study on the Loading Effects on the Atmospheric Pressure[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2003)
(  0) 0) |
| [3] |
张诗玉, 钟敏, 唐诗华. 我国GPS基准站地壳垂直形变的大气负荷效应[J]. 武汉大学学报:信息科学版, 2006, 31(12): 1090-1093 (Zhang Shiyu, Zhong Min, Tang Shihua. Vertical Crustal Displacements Due to Atmospheric Loading Effects at GPS Fiducial Stations in China[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1090-1093)
(  0) 0) |
| [4] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797
(  0) 0) |
| [5] |
Longman I M. A Green's Function for Determining the Deformation of the Earth under Surface Mass Loads[J]. Journal of Geophysical Research, 1962, 67(2): 845-850
(  0) 0) |
| [6] |
Spratt R S. Modeling the Effect of Atmospheric Pressure Variations on Gravity[J]. Geophysical Journal International, 2010, 71(1): 173-186
(  0) 0) |
| [7] |
Mangiarotti S, Cazenave A, Soudarin L, et al. Annual Vertical Crustal Motions Predicted from Surface Mass Redistribution and Observed by Space Geodesy[J]. Journal of Geophysical Research:Solid Earth, 2001, 106(B3): 4277-4292
(  0) 0) |
| [8] |
Mitrovica J X, Davis J L, Shapiro I I. A Spectral Formalism for Computing Three-Dimensional Deformations Due to Surface Loads: 2. Present-Day Glacial Isostatic Adjustment[J]. Journal of Geophysical Research :Solid Earth, 1994, 99(B4): 7075-7101
(  0) 0) |
| [9] |
沈迎春, 闫昊明, 彭鹏, 等. 质量负荷引起地表形变的格林函数和球谐函数方法对比研究[J]. 武汉大学学报:信息科学版, 2017, 42(7): 1008-1014 (Shen Yingchun, Yan Haoming, Peng Peng, et al. Comparative Study of Green's Function and Spherical Harmonic Function Methods on Surface Deformation Caused by Mass Loading[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 1008-1014)
(  0) 0) |
| [10] |
王伟, 党亚民, 章传银, 等. 基于CORS站网监测三峡地区陆地水负荷对地壳形变和重力变化的影响[J]. 地球物理学报, 2017, 60(3): 962-971 (Wang Wei, Dang Yamin, Zhang Chuanyin, et al. Monitoring of Crustal Deformation and Gravity Variation from Terrestrial Water Loading in the Three Gorges Region by the CORS Network[J]. Chinese Journal of Geophysics, 2017, 60(3): 962-971)
(  0) 0) |
| [11] |
党亚民. 现代大地测量基准[M]. 北京: 测绘出版社, 2015 (Dang Yamin. Modern Geodetic Datum[M]. Beijing: Surveying and Mapping Press, 2015)
(  0) 0) |
| [12] |
郭春喜, 宁津生, 陈俊勇, 等. 珠峰地区似大地水准面精化与珠峰顶正高的确定[J]. 地球物理学报, 2008, 51(1): 101-107 (Guo Chunxi, Ning Jinsheng, Chen Junyong, et al. Improvement of Regional Quasi-Geoid in Qomolangma(Mt. Everest) and Determination of Orthometric Elevation[J]. Chinese Journal of Geophysics, 2008, 51(1): 101-107 DOI:10.3321/j.issn:0001-5733.2008.01.013)
(  0) 0) |
| [13] |
Ray R D, Ponte R M. Barometric Tides from ECMWF Operational Analyses[J]. Ann Geophys, 2003, 21(8): 1897-1910
(  0) 0) |
2. Chinese Academy of Surveying & Mapping, 28 West-Lianhuachi Road, Beijing 100830, China
 2019, Vol. 39
2019, Vol. 39

