2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 南昌市广兰大道 418 号, 330013;
3. 江西省数字国土重点实验室, 南昌市广兰大道418号, 330013
病态问题在控制网平差、卫星快速定位、航空重力向下延拓等领域的数据处理时经常碰到。当系数矩阵列向量为复共线性相关时,最小二乘估计(least squares, LS)虽然为无偏估计,但参数估值已严重失真,不是最优解[1]。解决病态问题的常用方法有截断奇异值法[2](truncated singular value decomposition, TSVD)、Tikhonov正则化法[3-4]、岭估计法[5]等。截断奇异值法是基于奇异值分解技术的病态方程的一种直接解法,其原理是将较小的奇异值删除,保留较大的奇异值进行解算[6]。Tikhonov正则化法是在LS估计准则上加入稳定泛函约束条件,目的是将模型由严重病态变成病态性较弱或无病态,牺牲LS估计的无偏性,引入一定偏差使得方差降低,参数估值稳定可靠。正则化法和岭估计法都需要引入参数来调节法矩阵和正则化矩阵的相关关系,参数可由L-曲线[7-8]、岭迹法[9]、广义交叉核实法(generalized cross validation, GCV)[10-11]等方法确定。岭估计法是正则化法的一种简化特例,即将正则化矩阵换成单位阵,通过合理地选择正则化参数和正则化矩阵,可以提高参数估计的可靠性和稳定性。
Tikhonov正则化法和岭估计法都是有偏估计,在降低方差的同时引入偏差。林东方等[6]分析了岭估计的偏差和方差,提出一种确定正则化矩阵的方法,在降低方差的同时避免不必要的偏差,使得估值更为合理。shen等[12]、徐天问等[13]提出以均方误差作为衡量参数估值可靠性指标,定义均方误差是方差迹与偏差迹之和。林东方等[14]提出引入偏差量小于降低方差量的思想,在降低方差的同时控制偏差的引入,更为合理地解决病态问题。根据均方误差最小原则,为合理分配方差与偏差,本文提出岭估计迭代法。首先对病态数据用岭估计法求解,然后将岭估计解代入观测模型,更新观测向量,再次用岭估计法计算参数估值,以此形成迭代。通过分析迭代估计结果的方差、估计偏差及其变化趋势将均方误差最小或收敛作为迭代终止条件,并用模拟算例验证该方法的有效性与可行性,最后分析估值的估计偏差和实际偏差的关系。
1 岭估计法对于经典平差模型:
| $ \mathit{\boldsymbol{L}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} = \mathit{\boldsymbol{AX}} $ | (1) |
式中,L为观测值,A为系数矩阵,X为待定参数,Δ为观测向量的噪声,Δ~N(0, σ02 I),σ02是单位权方差。其最小二乘估计及其协方差为:
| $ \mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (2) |
| $ {\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\hat X}}} \right) = \sigma _0^2{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}} $ | (3) |
最小二乘估计是无偏估计,方差可由协方差矩阵之迹表示:
| $ D\left( {\mathit{\boldsymbol{\hat X}}} \right) = {\rm{tr}}\left[ {{\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\hat X}}} \right)} \right] = \sigma _0^2\sum\limits_{i = 1}^n {\frac{1}{{\lambda _i^2}}} $ | (4) |
式中, λi是系数矩阵A的奇异值。当法矩阵ATA出现病态(条件数一般大于103,条件数等于λmax2/λmin2),即存在λi接近0,从式(4)可以看出,方差将变得异常大,并且法矩阵求逆将会表现得很不稳定,导致求解出的参数估值不可靠[11]。
在解决系数矩阵病态问题时,Tikhonov正则化方法加入了稳定泛函Ω(X),相应的准则为:
| $ \begin{array}{*{20}{c}} {\left\| {\mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{L}}} \right\|_2^2 + \alpha \mathit{\Omega }\left( \mathit{\boldsymbol{X}} \right) = }\\ {\left\| {\mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{L}}} \right\|_2^2 + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{RX}} = \min } \end{array} $ | (5) |
式中,R为正则化矩阵,‖·‖为欧氏2-范数,α为大于0的正则化参数。当R = I则为岭估计,岭估计是正则化方法的一种特殊简化形式,其平差结果为:
| $ {{\mathit{\boldsymbol{\hat X}}}_0} = {\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (6) |
其中,N = ATA,则岭估计的方差、偏差分别为:
| $ \begin{array}{*{20}{c}} {D\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) = {\rm{tr}}\left[ {{\mathop{\rm cov}} \left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right)} \right] = {\rm{tr}}\left[ {{{\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)}^{ - 1}} \cdot } \right.}\\ {\left. {\mathit{\boldsymbol{N}}{{\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)}^{ - 1}}} \right] = \sigma _0^2\sum\limits_{i = 1}^n {\frac{{\lambda _i^2}}{{{{\left( {\lambda _i^2 + \alpha } \right)}^2}}}} } \end{array} $ | (7) |
| $ {\rm{bias}}\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) = \mathit{\boldsymbol{\tilde X}} - E\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) = \alpha {\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{\tilde X}} $ | (8) |
式中,
| $ {\rm{MSE}}\left( {\mathit{\boldsymbol{\hat X}}} \right) = E{\left( {\mathit{\boldsymbol{\tilde X}} - \mathit{\boldsymbol{\hat X}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{\tilde X}} - \mathit{\boldsymbol{\hat X}}} \right) $ | (9) |
则岭估计解均方误差为:
| $ \begin{array}{*{20}{c}} {{\rm{MSE}}\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) = D\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) + {\rm{tr}}\left( {{\rm{bias}}\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right){\rm{bias}}{{\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right)}^{\rm{T}}}} \right) = }\\ {\sigma _0^2{\rm{tr}}\left[ {{{\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)}^{ - 1}}\mathit{\boldsymbol{N}}{{\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)}^{ - 1}}} \right] + }\\ {\sigma _0^2{\rm{tr}}\left[ {{{\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)}^{ - 1}}\mathit{\boldsymbol{\tilde X}}{{\mathit{\boldsymbol{\tilde X}}}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)}^{ - 1}}} \right]} \end{array} $ | (10) |
对比分析式(4)、式(7)、式(10)可知,岭估计有效地降低了方差,却引入了偏差。因此,在处理病态数据时以均方误差作为衡量参数估值可靠性指标,降低方差的同时需要合理地控制偏差的引入量,让方差和偏差合理分配,使得参数估值稳定可靠。
2 岭估计迭代法在有偏估计中,方差与偏差并存。林东方等[14]提出引入偏差量小于降低方差量的思想,在降低方差的同时控制偏差的引入,更为合理地解决病态问题。参数估值的均方误差是方差之迹与偏差之迹的和,当参数估值的方差降低量大于偏差引入量时视为有效解。要得到最优有效解,则需均方误差最小。根据均方误差最小原则,合理分配方差与偏差,本文提出岭估计迭代解法。
观测模型如式(1),则岭估计解为:
| $ {{\mathit{\boldsymbol{\hat X}}}_0} = {\left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (11) |
将
| $ {{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = {\left( {\mathit{\boldsymbol{N}} + {\alpha _{k + 1}}\mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_k} $ | (12) |
迭代初值
若迭代矩阵的谱半径小于1,则迭代可以收敛[15-16]。本文岭估计迭代法的迭代矩阵为(N+αiI)-1 ATA,在对其特征值分解得到其特征值为Λf/(Λf+αi)。谱半径是方阵的最大特征值,而迭代矩阵的特征值均小于1,因此迭代是可以收敛的。
与一般迭代公式终止条件不同,本文迭代式终止条件并不是‖
岭估计迭代法相比于岭估计在迭代过程中逐渐降低方差,然而也逐渐提高了偏差。
由式(12)可以得到:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_k} = {{\left( {\mathit{\boldsymbol{N}} + {\alpha _k}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}{{\left( {\mathit{\boldsymbol{N}} + {\alpha _{k - 1}}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} \cdots }\\ {\left( {\mathit{\boldsymbol{N}} + {\alpha _0}\mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \end{array} $ | (13) |
根据协方差传播定律[16]可得协方差矩阵:
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\mathop{\rm cov}} \left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) = {{\left( {\mathit{\boldsymbol{N}} + {\alpha _k}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}{{\left( {\mathit{\boldsymbol{N}} + {\alpha _{k - 1}}\mathit{\boldsymbol{I}}} \right)}^{ - 1}} \cdot }\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} \cdots {{\left( {\mathit{\boldsymbol{N}} + {\alpha _0}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}{{\left( {\mathit{\boldsymbol{N}} + {\alpha _0}\mathit{\boldsymbol{I}}} \right)}^{ - 1}} \cdots } \end{array}}\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}{{\left( {\mathit{\boldsymbol{N}} + {\alpha _{k - 1}}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}{{\left( {\mathit{\boldsymbol{N}} + {\alpha _k}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}} \end{array} $ | (14) |
方差可由协方差矩阵之迹表示为:
| $ \begin{array}{*{20}{c}} {D\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) = {\rm{tr}}\left[ {{\mathop{\rm cov}} \left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right)} \right] = }\\ {\sigma _0^2\sum\limits_{i = 1}^n {\frac{{\mathit{\Lambda }_i^{2k + 1}}}{{{{\left[ {\left( {{\mathit{\Lambda }_i} + {\alpha _n}} \right)\left( {{\mathit{\Lambda }_i} + {\alpha _{n - 1}}} \right) \cdots \left( {{\mathit{\Lambda }_i} + {\alpha _0}} \right)} \right]}^2}}}} } \end{array} $ | (15) |
式中,Λi是法矩阵ATA的特征值。与式(7)相比,可知:
| $ D\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) < D\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) $ | (16) |
随迭代次数增加,岭估计迭代解将逐渐降低方差,而其偏差为:
| $ \begin{array}{*{20}{c}} {{\rm{bias}}\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) = \mathit{\boldsymbol{\tilde X}} - E\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) = \mathit{\boldsymbol{\tilde X}} - {{\left( {\mathit{\boldsymbol{N}} + {\alpha _k}\mathit{\boldsymbol{I}}} \right)}^{ - 1}} \cdot }\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{N}} + {\alpha _{k - 1}}\mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} \cdots \left( {\mathit{\boldsymbol{N}} + {\alpha _0}\mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A\tilde X}} = }\\ {\left[ {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{G}}_i}\left( {1 - \frac{{\mathit{\Lambda }_i^{n + 1}}}{{\left( {{\mathit{\Lambda }_i} + {\alpha _n}} \right)\left( {{\mathit{\Lambda }_i} + {\alpha _{n - 1}}} \right) \cdots \left( {{\mathit{\Lambda }_i} + {\alpha _0}} \right)}}} \right)\mathit{\boldsymbol{G}}_i^{\rm{T}}} } \right]\mathit{\boldsymbol{\tilde X}}} \end{array} $ | (17) |
式中,Gi为法矩阵ATA的特征向量,
| $ {\rm{bias}}\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) > {\rm{bias}}\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) $ | (18) |
因此,可以得到
| $ \begin{array}{*{20}{c}} {{\rm{MSE}}\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) = D\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) + {\rm{tr}}\left[ {{\rm{bias}}{{\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right)}^{\rm{T}}}{\rm{bias}}\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right)} \right] = }\\ {\sigma _0^2\sum\limits_{i = 1}^n {\frac{{\mathit{\Lambda }_i^{2k + 1}}}{{{{\left[ {\left( {{\mathit{\Lambda }_i} + {\alpha _n}} \right)\left( {{\mathit{\Lambda }_i} + {\alpha _{n - 1}}} \right) \cdots \left( {{\mathit{\Lambda }_i} + {\alpha _0}} \right)} \right]}^2}}}} + }\\ {\sum\limits_{i = 1}^n {{{\mathit{\boldsymbol{\tilde X}}}^{\rm{T}}}{\mathit{\boldsymbol{G}}_i}} }\\ {\left( {1 - \frac{{\mathit{\Lambda }_i^{2k + 2}}}{{{{\left[ {\left( {{\mathit{\Lambda }_i} + {\alpha _n}} \right)\left( {{\mathit{\Lambda }_i} + {\alpha _{n - 1}}} \right) \cdots \left( {{\mathit{\Lambda }_i} + {\alpha _0}} \right)} \right]}^2}}}} \right)\mathit{\boldsymbol{G}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde X}}} \end{array} $ | (19) |
由于各种参数均未知,本文方法与岭估计的均方误差无从比较。因此,为了体现本文方法的优势,将计算过程中均方误差达到最小值或收敛于某一值作为迭代终止条件:
| $ {\rm{MSE}}\left( {{{\mathit{\boldsymbol{\hat X}}}_k}} \right) = D\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) - \sum\limits_{j = 1}^k {{d_j}} + B\left( {{{\mathit{\boldsymbol{\hat X}}}_0}} \right) + \sum\limits_{j = 1}^k {{b_j}} $ | (20) |
式中, D(
下面给出本文方法的解算步骤:
1) 选择L-曲线法或其他方法确定岭参数,计算出岭估计解
2) 将计算出的
3) 再次用L-曲线法或其他方法选择岭参数,再计算出岭估计解
4) 重复步骤1)、2)、3);
5) 因为要求得最小均方误差,而不知道第几次迭代得到最小值,所以计算时先任取一迭代次数,在迭代过程中计算出参数估值和求出其均方误差,并观察均方误差变化趋势,当均方误差最小或收敛时,此时的估值就为最优有效解。
4 算例及分析 4.1 算例1采用文献[17]中的模拟病态问题算例,法矩阵条件数为2.083 8×104,严重病态。未知参数有5个,X=[x1 x2 x3 x4 x5]T,真值为X=[1 1 1 1 1]T,观测值L的噪声Δ~N(0, σ02I), σ0=1(具体数据未列出,详情可见参考文献)。分别用最小二乘、岭估计、截断奇异值法和本文方法进行平差解算,本文方法按照上述方法的解算步骤计算,先确定迭代次数(10、100、1 000、3 000、5 000),再根据均方误差变化趋势确定合理迭代次数。各方法结果、估计均方误差MSE(
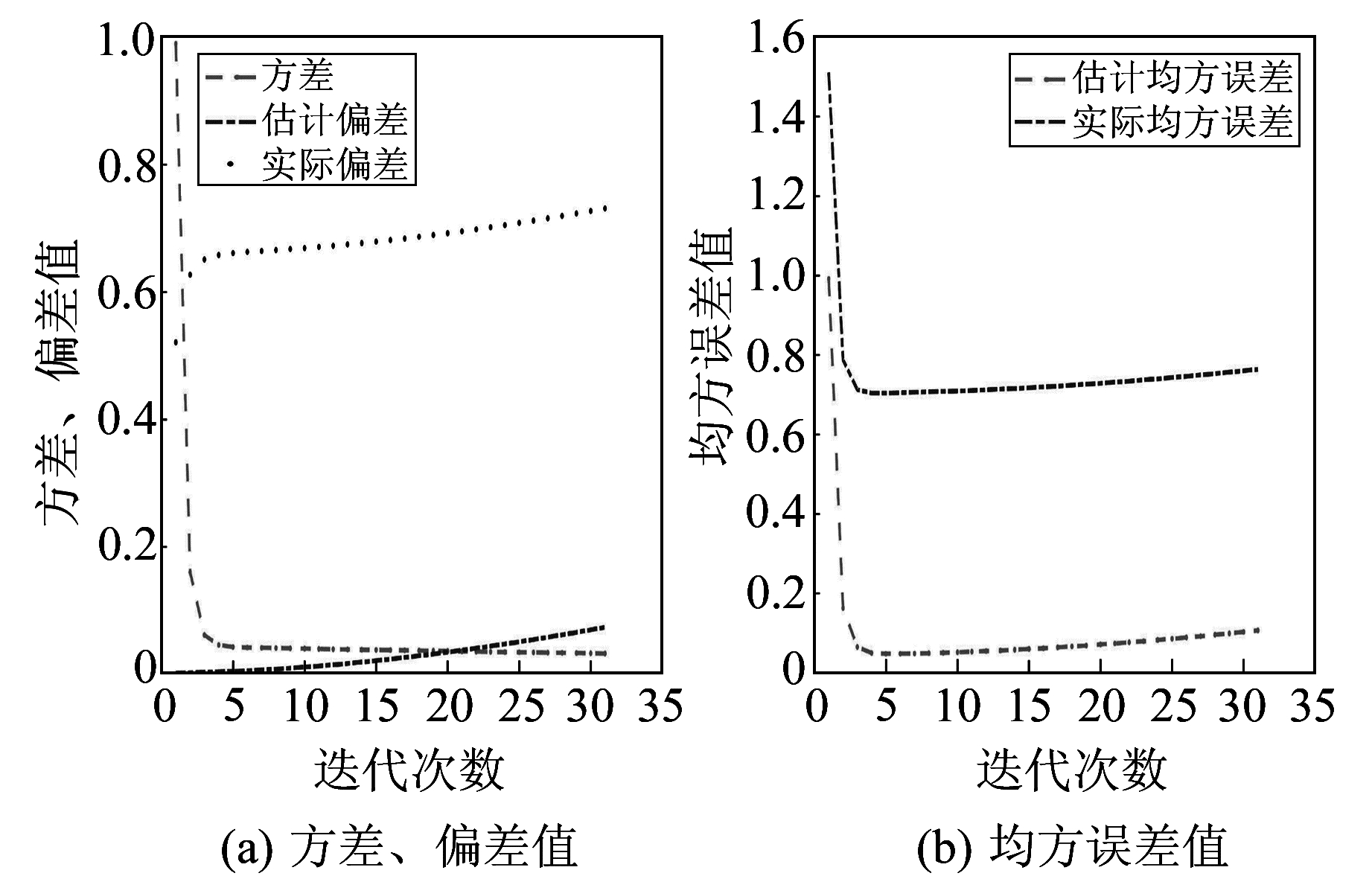
|
图 1 方差、偏差、均方误差变化趋势 Fig. 1 Variance, deviation, mean square error change trend |
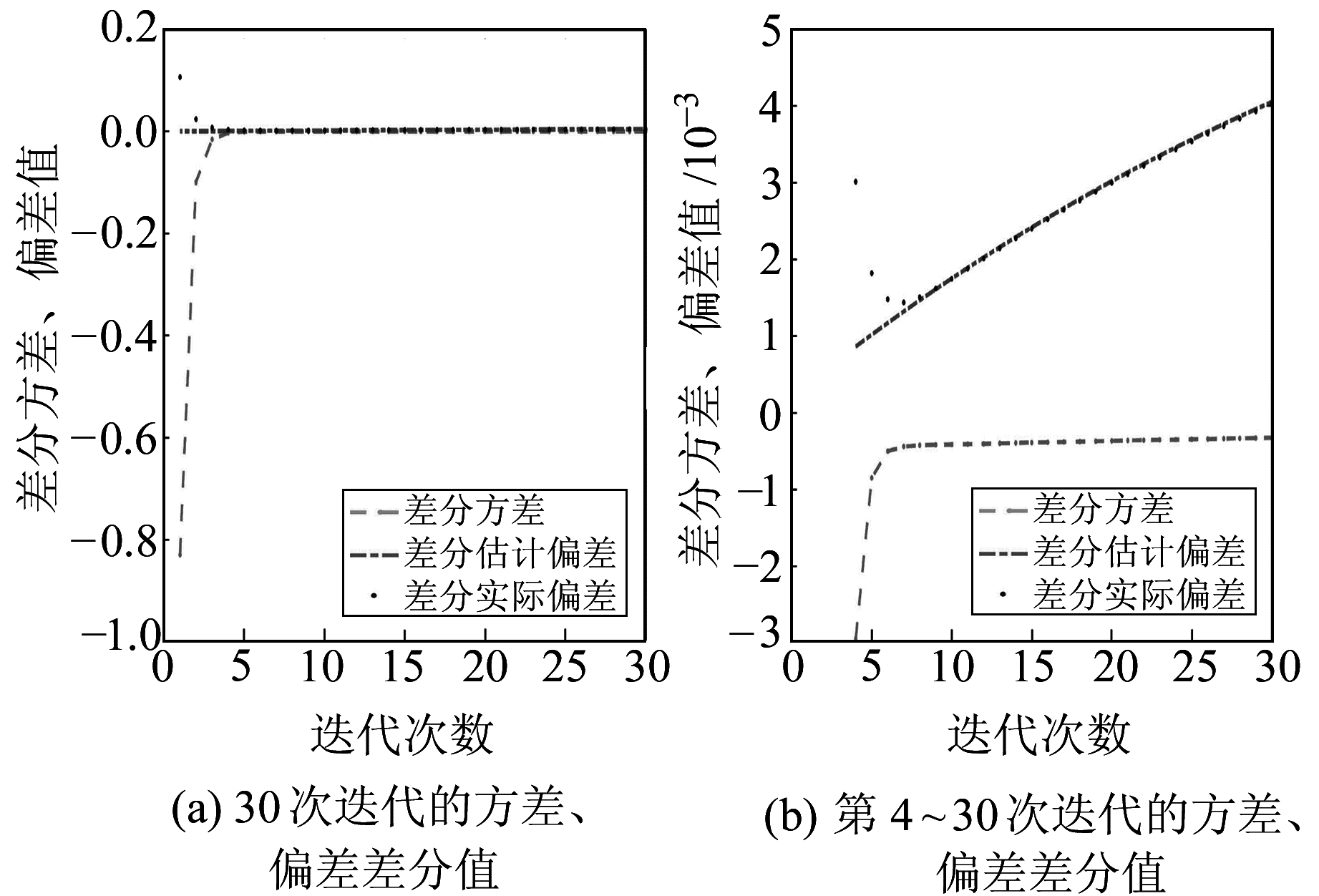
|
图 2 方差和偏差差分值对比 Fig. 2 Variance and deviation difference score |
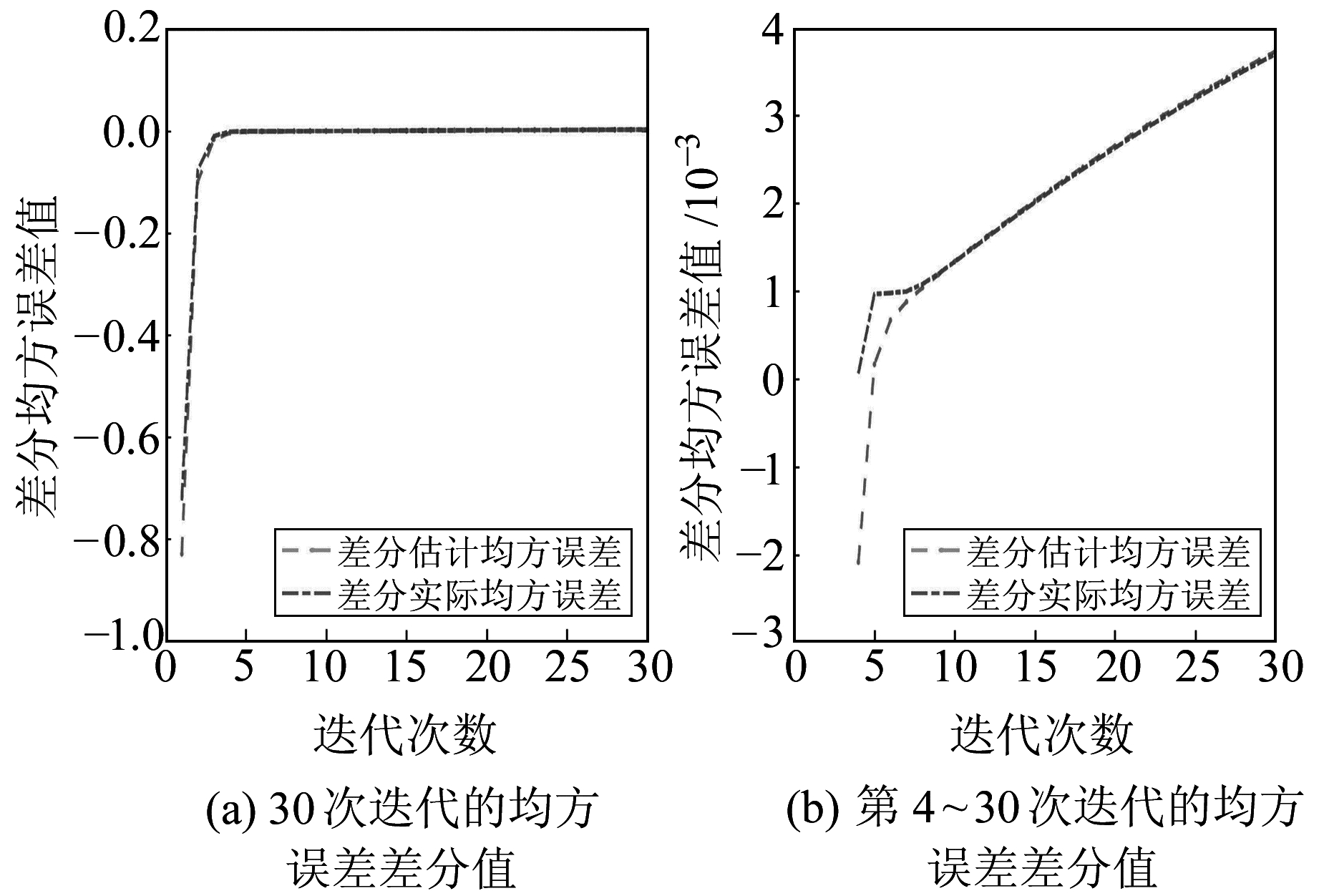
|
图 3 均方误差差分值 Fig. 3 Difference of mean squared error |
|
|
表 1 不同方法的结果 Tab. 1 Results of different estimations |
采用文献[18]模拟空间测边网算例。P1、P2、…、P10为10个已知点,其坐标具体数据略去,10个已知点到3个未知点P11、P12、P13(假设模拟坐标真值分别为(0 m,0 m,0 m)、(68 m,-26 m,9 m)和(14 m,41 m,-11 m))的距离以及3个未知点间的距离假定已通过测量得到。设各距离为等精度观测,中误差为±0.01 m。根据33个距离观测值确定3个未知点坐标。计算中3个未知点坐标近似值分别取(0.03 m,-0.025 m,0.01 m)、(68.03 m,-25.97 m,8.98 m)和(14.04 m,40.97 m,-11.04 m)。该测边网所建立观测方程的系数阵A严重病态,法矩阵条件数为89 543。根据计算步骤,先确定迭代次数(10、100、1 000、3 000、5 000),再根据均方误差变化趋势确定合理迭代次数。各种算法结果、估计均方误差、实际均方误差及差值范数等见图 4~6及表 2。

|
图 4 方差、偏差、均方误差及变化趋势 Fig. 4 Variance, deviation, mean square error change trend |
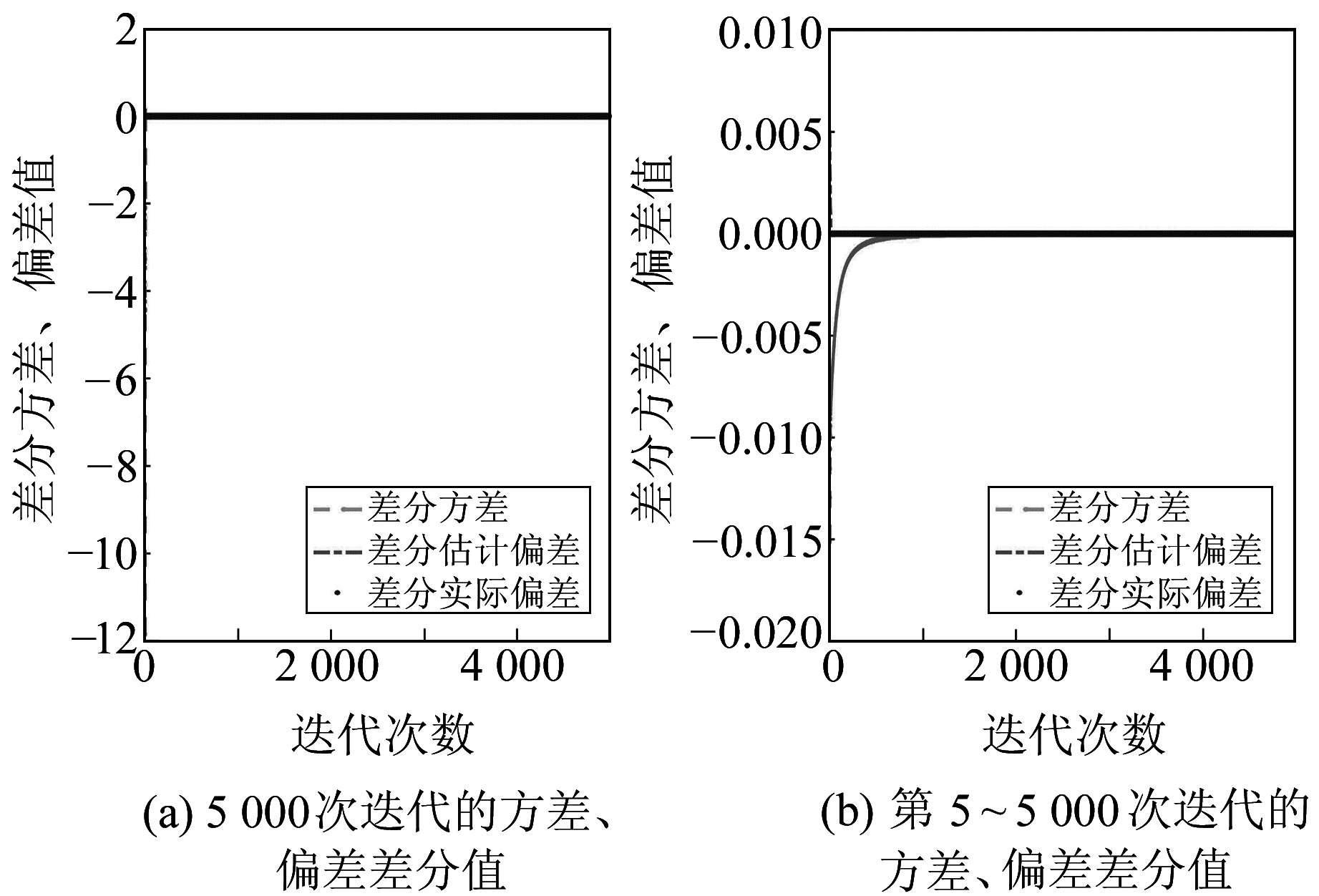
|
图 5 方差和偏差差分值对比 Fig. 5 Variance and deviation difference score |
|
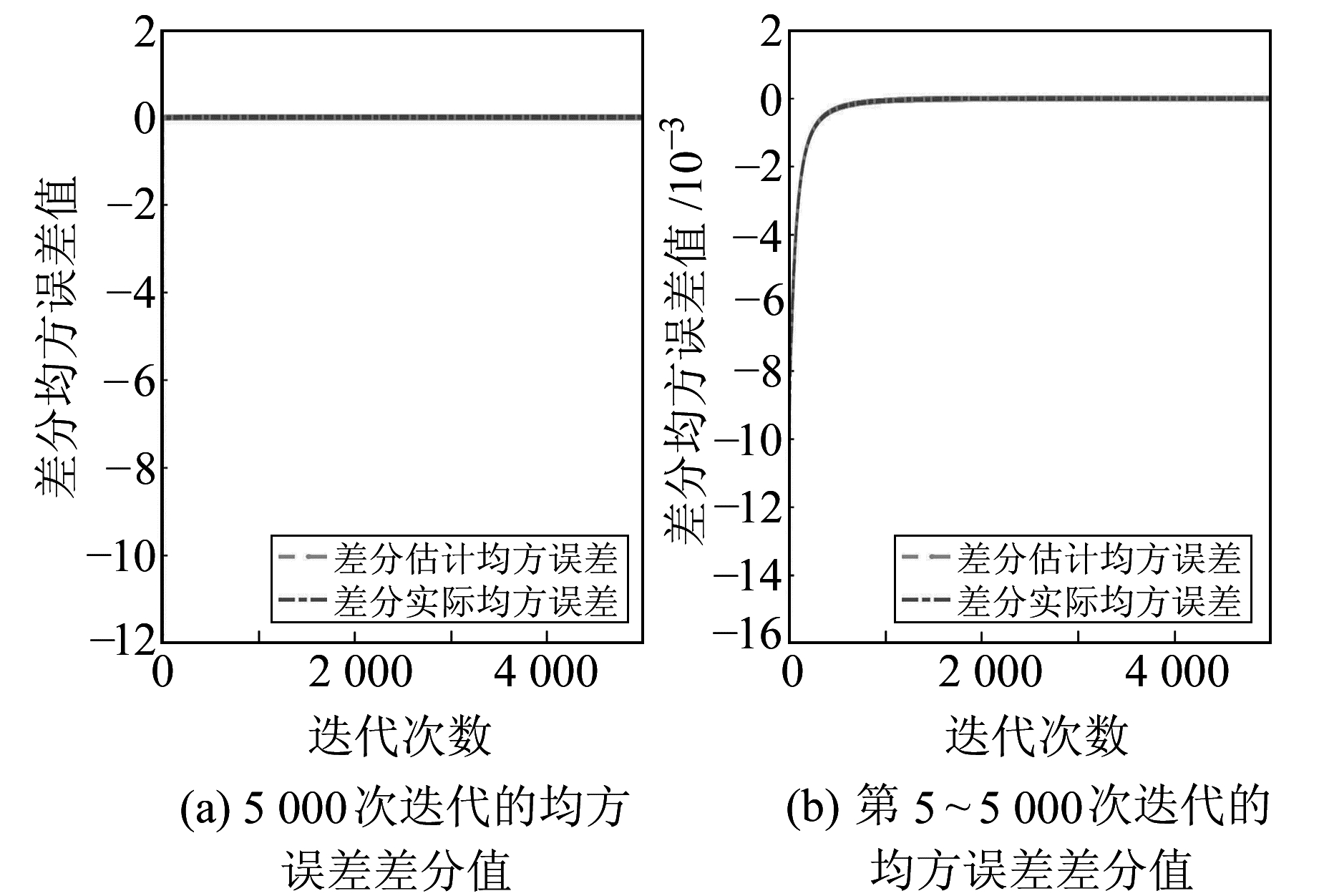
图 6 均方误差差分值 Fig. 6 Difference of mean squared error |
|
|
表 2 多种方法参数估计结果 Tab. 2 Results of different estimations |
由于本文算法是先任取迭代次数,经多次反复计算,算例1虽然在前几次迭代的结果已符合方法要求,但为了具体分析问题,最终选择30次迭代,记录结果并作出方差、偏差、均方误差及差分图表。算例2在迭代1 000次左右变化缓慢,从1 000次到3 000次迭代,结果变化非常小,从3 000次到5 000次迭代,结果基本不变,因此最终选择5 000次迭代。
从图 1(a)、图 4(a)可以看出,方差在降低,估计偏差与实际偏差在增加,变化情况与分析一致。算例1在前5次迭代计算中,方差下降较快,估计偏差与实际偏差增长也快;之后方差降低非常缓慢,而估计偏差与实际偏差依然增加。方差的降低量、估计偏差与实际偏差的增加量均大于方差的降低量,再继续计算均方误差将增大。算例2在前5次迭代计算中,方差下降较快,偏差增加较快;迭代几百次之后,方差降低较为缓慢,而偏差增加也非常缓慢,再之后的迭代中,方差与偏差变化均非常小,迭代结果仍有细小变化,一定的迭代次数之后就有可见变化。从图 4(b)可以看出,估计均方误差与实际均方误差均在减小且前几次迭代降低较快之后缓慢直至收敛。
图 2、图 3、图 5、图 6是方差与偏差的差分图,由差分图可进一步得出均方误差的变化情况。由图可见,方差、偏差及均方误差前几次迭代结果变化较快,之后则是均匀变化。在以均方误差作为衡量参数估值的标准时,算例1第5次迭代值为最优解;算例2迭代到5 000次时,结果基本不变,所以取第5 000次迭代值为最优解。从表 1可以看出,岭估计和本文方法的估计均方误差分别是0.991 7、0.048 0,实际均方误差分别为1.510 8、0.704 4;表 2的岭估计和本文方法的估计均方误差分别是22.704 7、0.496 5,实际均方误差分别为22.684 5、0.001 4,可见本文方法的均方误差比岭估计低;相比岭估计,算例1、算例2中本文方法差值范数也有所降低,最终结果比TSVD更优且均方误差更小。
本文在计算估计偏差时采用岭估计的估值代替真值,而从图 1(a)、图 2(b)、图 4(a)、图 5(b)可以看出,虽然估计偏差与实际偏差有一定的差值,但除前几次迭代偏差变化较大之外,之后迭代中两者的变化情况高度一致,规律相似。可以得出,估计均方误差与实际均方误差虽然有差值,但两者增加或减少的规律是一致的,在均方误差意义下,当估计均方误差达到最小时,其实际均方误差也将达到最小。因此,可以采用岭估计的估值代替真值求解均方误差。
在病态数据处理中,相较于岭估计,本文岭估计迭代法能有效地提高参数估值的稳定性、可靠性,进一步降低均方误差和差值范数,更具优势。
5 结语本文岭估计迭代法在迭代计算中可使方差逐渐降低,偏差逐渐增加。根据林方东等[14]提出的方差降低量大于偏差引入量的思想,若dj>bj,则结果有效,直到dj≤bj迭代终止,此时均方误差最小。通过合理次数的迭代计算得到最小或收敛的均方误差,取此时的参数估值为最优解,并用算例验证该方法,计算得到的均方误差、差值范数以及参数估值均优于LS估计、岭估计和TSVD,说明该方法有效、可行。
岭估计迭代法需要先选择迭代次数,可通过选择不同迭代次数,作出均方误差变化趋势图,一步步确定合理的迭代次数,根据图形选出最小或收敛的均方误差。迭代过程虽较为复杂,但可用MATLAB等计算软件编程实现,自动找出最小均方误差和相应的参数估值,故本文方法对计算效率无太大影响。在算例2中,本文为更好地说明问题而选择的迭代次数过多,在解决实际问题时,无需像算例2一样过多迭代,当迭代收敛时,设定一阈值终止迭代即可。b
| [1] |
崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2009 (Cui Xizhang, Yu Zongchou, Tao Benzao, et al. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [2] |
Xu P L. Truncated SVD Methods for Discrete Linear Ill-Posed Problems[J]. Geophysical Journal International, 1998, 135(2): 505-514 DOI:10.1046/j.1365-246X.1998.00652.x
(  0) 0) |
| [3] |
Tikhonov A N. Solution of Incorrectly Formulated Problems and the Regularization Method[J]. Soviet Math Dokl, 1963(4): 1035-1038
(  0) 0) |
| [4] |
Tikhonov A N, Arsenin V Y. Solutions of Ill-Posed Problems[J]. Mathematics of Computation, 1977, 32(144): 491-491
(  0) 0) |
| [5] |
Hoerl A E, Kennard R W. Ridge Regression: Biased Estimation for Nonorthogonal Problems[J]. Technometrics, 1970, 12(1): 55-67 DOI:10.1080/00401706.1970.10488634
(  0) 0) |
| [6] |
林东方, 朱建军, 宋迎春, 等. 正则化的奇异值分解参数构造法[J]. 测绘学报, 2016, 45(8): 883-889 (Lin Dongfang, Zhu Jianjun, Song Yingchun, et al. Construction Method of Regularization by Singular Value Decomposition of Design Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 883-889)
(  0) 0) |
| [7] |
Hansen P C. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve[J]. SIAM Review, 1992, 34(4): 561-580 DOI:10.1137/1034115
(  0) 0) |
| [8] |
Hansen P C, O'Leary D P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems[J]. SIAM J Sci Comput, 1993, 14(6): 1487-1503 DOI:10.1137/0914086
(  0) 0) |
| [9] |
陈希孺, 王松桂. 近代回归分析——原理方法及应用[M]. 合肥: 安徽教育出版社, 1987 (Chen Xiru, Wang Songgui. Modern Regression Analysis[M]. Hefei: Anhui Education Press, 1987)
(  0) 0) |
| [10] |
Golub G H, Heath M, Wahba G. Generalized Crossvalidation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics, 1979, 21(2): 215-223 DOI:10.1080/00401706.1979.10489751
(  0) 0) |
| [11] |
Sourbron S, Luypaert R, Van Schuerbeek P, et al. Choice of the Regularization Parameter for Perfusion Quantification with MRI[J]. Physics in Medicine & Biology, 2004, 49(14): 3307-3324
(  0) 0) |
| [12] |
Shen Y Z, Xu P L, Li B F. Bias-Corrected Regularized Solution to Inverse Ill-Posed Models[J]. Journal of Geodesy, 2012, 86(8): 597-608 DOI:10.1007/s00190-012-0542-y
(  0) 0) |
| [13] |
徐天河, 杨元喜. 均方误差意义下正则化解优于最小二乘解的条件[J]. 武汉大学学报:信息科学版, 2004, 29(3): 223-226 (Xu Tianhe, Yang Yuanxi. Condition of Regularization Solution Superior to LS Solution Based on MSE Principle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 223-226)
(  0) 0) |
| [14] |
林东方, 朱建军, 宋迎春. 顾及截断偏差影响的TSVD截断参数确定方法[J]. 测绘学报, 2017, 46(6): 679-688 (Lin Dongfang, Zhu Jianjun, Song Yingchun. Truncation Method for TSVD with Account of Truncation Bias[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 679-688)
(  0) 0) |
| [15] |
王泽文, 邱淑芳, 阮周生. 数值分析与算法[M]. 北京: 科学出版社, 2016 (Wang Zewen, Qiu Shufang, Ruan Zhousheng. Numerical Analysis and Algorithms[M]. Beijing: Science Press, 2016)
(  0) 0) |
| [16] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2003 (Department of Surveying Adjustment, School of Geodesy and Geomatics, Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2003)
(  0) 0) |
| [17] |
鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉: 武汉大学, 2010 (Lu Tieding. Research on the Total Least Squares and Its Applications in Surveying Data Processing[D]. Wuhan: Wuhan University, 2010)
(  0) 0) |
| [18] |
郭建锋.测量平差系统病态性的诊断与处理[D].郑州: 信息工程大学, 2002 (Guo Jianfeng.The Diagnosis and Process of Ill-Conditioned Adjustment System[D]. Zhengzhou: Information Engineering University, 2002)
(  0) 0) |
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, 418 Guanglan Road, Nanchang 330013, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, 418 Guanglan Road, Nanchang 330013, China
 2019, Vol. 39
2019, Vol. 39


