支持向量回归机(support vector regression,SVR)是一种能够处理回归和模式识别等诸多问题的新型统计学方法[1],它在小样本、非线性以及高维模式识别问题中具有独特的优势,能很好地解决数据量少、过学习、局部极小点等实际难点,具有很强的泛化能力,被广泛应用到变形预测领域中。最小二乘支持向量回归机(least square support vector regression,LSSVR)是SVR的扩展,它将SVR中的二次规划问题转化为求解线性方程组的问题,简化了计算。但LSSVR的拟合精度和泛化性能受参数影响,即惩罚参数c和核函数参数σ的取值会直接决定LSSVR的推广功能。目前关于参数的确定方法主要有网格搜索法、交叉验证法、直接确定法[2]等。但这些参数优化方法均存在各自的缺点[3]:网格搜索法并不一定能得到最优参数且计算量大;交叉验证法同样需要大量计算,耗时长,不适用于实际生产;直接确定法要求有较高的先验知识。人工蜂群算法(artificial bee colony,ABC)是一种模拟蜂群协作寻找蜜源的生物智能优化算法[4],与GA、PSO等智能算法相比,ABC具有参数设置少、计算简单、更大概率得到最优解等优点。然而受制于算法结构,ABC存在搜索精度不高、收敛速度慢以及早熟收敛等缺点。
针对标准ABC的不足之处,本文提出一种正反双蜂群交叉寻优算法,利用反向学习策略生成正反2个种群来增加初始群体的多样性,并对双种群的当前最优食物源进行信息交换以实现优中选优。针对标准ABC搜索策略及概率选择的片面性,设计食物源自适应权重函数及适应度自适应选择函数平衡标准ABC的勘探和开发能力。以LSSVR的预测精度为目标函数,将改进后的人工蜂群算法(improved artificial bee colony,IABC)用于LSSVR中,实现对惩罚参数和核函数参数的优化,从而建立基于IABC-LSSVR的预测模型,最后将此模型应用于某基坑变形预测中进行检验。
1 基本理论介绍 1.1 最小二乘支持向量回归机LSSVR的基本思想是利用已知的样本数据得出一个最佳拟合函数,根据这个函数再输入新的样本数据,从而计算出对应的输出值。其具体步骤[5-6]如下。
给定训练集:
| $ T = \left\{ {\left( {{x_1},{y_1}} \right), \cdots ,\left( {{x_l},{y_l}} \right)} \right\} \in {\left( {{R^n} \times Y} \right)^l} $ | (1) |
式中,xi∈Rn,yi∈Y=R, i=1, 2,…, l。用非线性映射将样本输入映射到高维空间,构造出LSSVR的函数为:
| $ y\left( x \right) = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( x \right) + b $ | (2) |
式中,ω为权值向量,b为偏差。转化为优化问题:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\omega ,b,\xi } R = \frac{1}{2}{{\left\| \mathit{\boldsymbol{\omega }} \right\|}^2} + \frac{c}{2}\sum\limits_{i = 1}^l {{\xi ^2}} }\\ {{\rm{s}}.\;{\rm{t}}.\;\;\;{y_i} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right) + b + {\xi _i}} \end{array} $ | (3) |
式中,c为惩罚参数,ξi≥0为松弛因子。利用Lagrange函数和KKT优化条件可解得LSSVR的函数模型为:
| $ y\left( x \right) = \sum\limits_{i = 1}^l {{a_i}K\left( {x,{x_i}} \right)} + b $ | (4) |
式中, ai为Lagrange乘子,K(x,xi)为核函数。不同的实际问题需要选择不同的核函数,考虑到变形预测模型需较强的拟合能力,故本文采用具有较宽收敛域的Gauss径向基函数作为LSSVR的核函数:
| $ K\left( {x,{x_i}} \right) = \exp \left( { - \frac{{\left\| {x - {x_i}} \right\|_2^2}}{{2{\sigma ^2}}}} \right) $ | (5) |
标准ABC是根据蜜蜂采蜜的整个过程模拟出的一种智能算法。根据分工的不同,种群可分为引领蜂、跟随蜂和侦查蜂,引领蜂和跟随蜂各占整个蜂群规模的一半。蜜蜂在寻找食物源的过程可以被抽象成寻找问题最优解的过程[7],3种蜜蜂各司其职,以协同的方式高效完成寻优工作。其寻优原理[8]如下。
设蜜源xi(i=1,2,…,NP),xi的质量对应于解的适应度值fit,设求解问题的维数为D,迭代次数为t,最大迭代次数为T,则t次迭代时蜜源位置为xit=[xi1t,xi2t,…,xiDt],xid∈(Ld,Ud),即搜索空间的上下限。
1) 随机产生蜜源的初始位置:
| $ {x_{id}} = {L_d} + {\rm{rand}}\left( {0,1} \right)\left( {{U_d} - {L_d}} \right) $ | (6) |
2) 在初始蜜源的周围搜索,产生一个新的蜜源:
| $ {v_{id}} = {x_{id}} + \varphi \left( {{x_{id}} - {x_{jd}}} \right) $ | (7) |
式中,j=1,2,…,NP,且j≠i,φ是[-1, 1]均匀分布的随机数。
3) 评价2个蜜源的适应度,根据贪婪算法确定保留xi或vi:
| $ {\rm{fit}} = \left\{ \begin{array}{l} 1/\left( {1 + {f_i}} \right),{f_i} \ge 0\\ 1 + {\rm{abs}}\left( {{f_i}} \right),其他 \end{array} \right. $ | (8) |
式中,fi为解的函数值。
4) 计算引领蜂找到的蜜源被跟随的概率:
| $ {P_i} = {\rm{fi}}{{\rm{t}}_i}/\sum\limits_{i = 1}^{{\rm{NP}}} {{\rm{fi}}{{\rm{t}}_i}} $ | (9) |
5) 跟随蜂采用轮盘赌的方式选择引领蜂,即在[0, 1]内产生均匀分布的随机数r,当Pi>r,则跟随蜂在蜜源i周围产生一个新蜜源,利用贪婪算法确定保留的蜜源。判断蜜源是否满足被放弃的条件为:经t次迭代到达阈值limit仍没找到更好的蜜源,则放弃。
放弃:引领蜂变为侦查蜂,在搜索空间随机产生一个新蜜源代替xi:
| $ x_i^{t + 1} = \left\{ \begin{array}{l} {L_d} + {\rm{rand}}\left( {0,1} \right)\left( {{U_d} - {L_d}} \right),t \ge {\rm{limit}}\\ x_i^t,t < {\rm{limit}} \end{array} \right. $ | (10) |
不放弃:t=t+1,判断算法是否达到终止条件,输出最优解。
2 改进的人工蜂群算法为了提高标准ABC的种群多样性、全局收敛速度和收敛精度,本文在种群构造、搜索策略和蜜源选择概率等多个方面进行改进。
2.1 种群构造的改进Haupt等[9]认为,对群体智能优化算法而言,初始种群的好坏影响着算法的全局收敛速度和解的质量,多样性较好的初始种群对提高算法的寻优性能很有帮助。在标准ABC中,种群的初始化是随机的,无法保证其多样性。考虑到ABC对初始种群的构造方法较为敏感,本文提出一种正反双种群交叉寻优策略来构造种群。
1) 初始化一个种群A,并设其中一个解为a=(x1,x2,…xd),xi∈(mi,ni),则其反向解为b=(x'1,x'2,…x'd),其中x'i=mi+ni-xi,以此构造出种群A的反向种群B。
2) 对种群A和种群B分别进行一次寻优,得到当前最优值p1和p2。
3) 对双种群进行信息交换:
| $ \begin{array}{*{20}{c}} {{{p'}_1} = {p_1} + {\rm{rand}}\left( {0,1} \right)\left( {{p_1} - {p_2}} \right)}\\ {{{p'}_2} = {p_2} + {\rm{rand}}\left( {0,1} \right)\left( {{p_2} - {p_1}} \right)} \end{array} $ | (11) |
4) 根据贪婪算法选择p1或p'1作为种群A的当前最优值,选择p2或p'2作为种群B的当前最优值。
5) 达到最大迭代次数T,根据贪婪算法确定整个种群的最优值。
2.2 搜索策略的改进标准ABC的搜索机制是在食物源的附近随机搜索新食物源,这种更新方式不与优秀个体发生信息交流,所以导致收敛速度慢。韩建权等[7]也指出标准ABC算法具有较好的探索能力,但开发能力不足,局部搜索能力较弱,收敛速度相对较慢。为加快收敛速度,Zhu等[10]参考粒子群算法将全局最优解引入搜索公式中:
| $ {v_{id}} = {x_{id}} + {\varphi _1}\left( {{x_{id}} - {x_{jd}}} \right) + {\varphi _2}\left( {{y_d} - {x_{id}}} \right) $ | (12) |
式中,φ1∈(0, 1),φ2∈(0, 1.5),yd为全局最优解的第d个变量。
虽然引入全局最优解能加快收敛速度,但同时也会使种群快速向优秀食物源靠近而破坏整个种群的多样性,从而造成早熟现象,得不到全局最优解。所以为平衡种群多样性和收敛速度,本文设计一种新的食物源自适应权重函数ω1和ω2,得到新的搜索公式:
| $ \begin{array}{l} {v_{id}} = {x_{id}} + {w_1}{\varphi _1}\left( {{x_{id}} - {x_{jd}}} \right) + {w_2}{\varphi _2}\left( {{y_d} - {x_{id}}} \right)\\ \;\;\;\;\;\;\;{\omega _1} = {\omega _{\min }} + \left( {{\omega _{\max }} - {\omega _{\min }}} \right)\left( {1 - \frac{t}{T}} \right)\\ \;\;\;\;\;\;\;{\omega _2} = {\omega _{\max }} - \left( {{\omega _{\max }} - {\omega _{\min }}} \right)\left( {1 - \frac{t}{T}} \right) \end{array} $ | (13) |
式中,ωmin和ωmax均取常数,分别为权重函数的最小值和最大值,ω1为递减函数,ω2为递增函数。在算法初期,ω1>ω2,具有较好的勘探能力,可以挖掘出尽可能多的全局优秀解;随着迭代次数t的增加,在算法后期,ω2>ω1,此时算法已有较强的开发能力,可快速向全局最优解收敛。
2.3 蜜源选择概率的改进在标准ABC中只选择适应度高的蜜源,这无疑会导致种群的多样性下降,很难达到全局最优。针对这一缺点,本文设计一种适应度自适应选择函数来改进标准ABC的选择概率公式:
| $ \begin{array}{l} {P_i} = \frac{{{\rm{fit}}_i^\lambda }}{{\sum\limits_{i = 1}^{{\rm{NP}}} {{\rm{fit}}_i^\lambda } }}\\ \lambda = {{\rm{e}}^{\frac{t}{T}\ln 2}} - 1 \end{array} $ | (14) |
从改进的选择概率公式(14)可看出,算法前期,
将以上各方面改进内容引入标准ABC可得IABC流程,如图 1所示。

|
图 1 IABC算法流程 Fig. 1 Flowchart of IABC |
LSSVR中存在2个待优化的参数——惩罚参数c和核函数参数σ。以LSSVR的预测准确率为目标函数,将IABC与LSSVR相结合,用于变形预测模型的构建。具体实现步骤如下。
1) 数据预处理。归一化(mapminmax)到(0, 1)区间:
| $ y = \frac{{\left( {{y_{\max }} - {y_{\min }}} \right)\left( {x - {x_{\min }}} \right)}}{{{x_{\max }} - {x_{\min }}}} + {y_{\min }} $ | (15) |
2) 设置IABC的控制参数。包括蜂群数量NP,蜜源最大搜索次数limit,算法最大迭代次数T,自适应函数ω取值范围ωmax及ωmin,蜜源的维度即待优化参数的个数D及各参数的取值范围。
3) 设置适应度函数。变形预测的目的即为获取最小误差的预测值,故本文采用均方根误差函数作为目标函数,并将目标函数转化为适用于IABC的适应度函数。目标函数为:
| $ \min f\left( {c,\sigma } \right) = \sqrt {\frac{1}{l}\sum\limits_{i = 1}^l {{{\left[ {{y_i} - g\left( {{x_i},c,\sigma } \right)} \right]}^2}} } $ |
式中,l为样本数据集,yi为实测值,g为模型计算值。适应度函数为:
| $ {\rm{fi}}{{\rm{t}}_i} = \frac{1}{{1 + {f_i}}} $ |
4) 构造双种群。根据待优化参数的取值范围随机生成种群A,根据反向学习策略计算出对应的反向种群B,以此构造出双种群。
5) 根据IABC算法对双种群分别进行蜜源搜索、适应度计算以及信息交换等操作。
6) 达到最大迭代次数T,得到最优参数组合解。
7) 滚动预测。首先输入m期训练样本,预测出第m+1期变形数据,然后将已预测出的第m+1期数据加入训练样本,组成新的训练样本(同时保持训练样本期数不变)预测出第m+2期数据。以此类推,直到得出所有待预测样本。
4 工程实例以文献[11]中广州某基坑项目21期监测沉降数据为例,将前18期作为模型拟合数据,后3期作为预测数据。分别采用标准ABC-LSSVR、IABC-LSSVR以及文献[11]研究的PSO-GM-ARMA组合模型进行预测,并使用均方根误差(RMSE)比较各模型的预测效果。
将ABC-LSSVR及IABC-LSSVR共有参数设置为:人工蜂群规模NP=20,蜜源数量是蜂群规模的一半,求解问题的维数D=2,最大迭代次数T=100,最大搜索次数limit=50,惩罚参数c和核函数参数σ取值范围为(0.01, 100)。IABC-LSSVR特有参数设置为:自适应搜索平衡参数ω、概率选择调整参数λ取值范围为(0,100)。根据IABC-LSSVR的建模步骤,运用MATLAB编写程序,分别得到各模型的种群进化图(图 2),以及各模型的预测效果(表 1、图 3)。
|
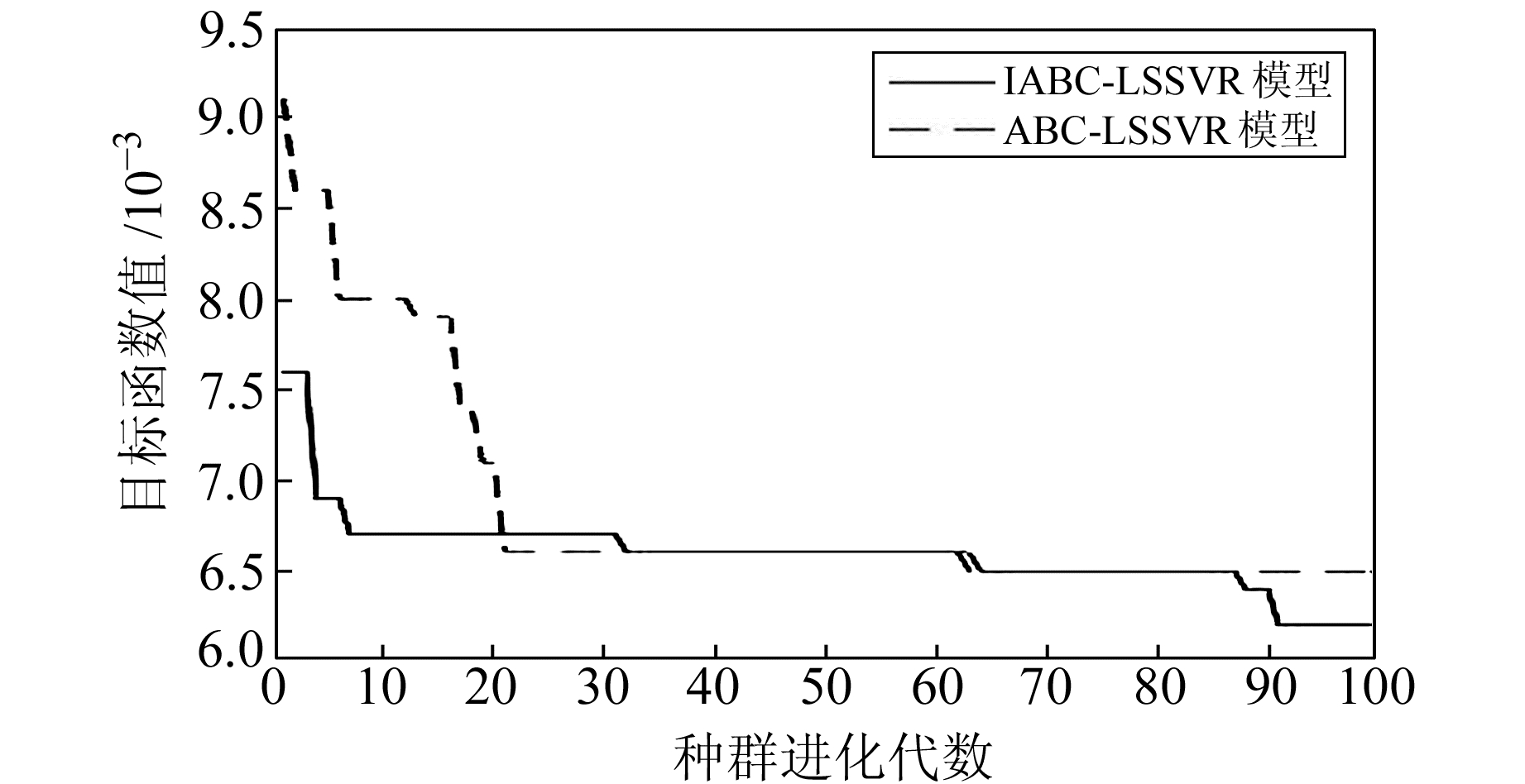
图 2 IABC-LSSVR与ABC-LSSVR预测进化图 Fig. 2 Predictive evolutionary graph of IABC-LSSVR and ABC-LSSVR |
|
|
表 1 各预测模型效果对比 Tab. 1 Comparison of the effects of different forecasting models |

|
图 3 各模型预测结果 Fig. 3 The prediction results of each model |
由图 2可知,从第1代起,IABC的目标函数值就低于ABC,说明本文构造的正反初始种群通过信息交换得到了更好的蜜源,实现了优中选优。随着迭代次数的增加,ABC算法大约在20代便达到其收敛值,而IABC在10~70代之间达到平稳状态,之后又迅速收敛。说明本文设计的自适应搜索策略及自适应概率选择逐步凸显效果,在前期保留适应度低的食物源,后期迅速向最优食物源靠近,从而达到先增加种群多样性后提高全局收敛精度的要求。
由表 1可知,ABC-LSSVR模型预测结果均方根误差为±0.033;王显鹏等[11]研究的PSO-GM-ARMA组合模型预测结果均方根误差为±0.03;本文构建的IABC-LSSVR模型预测结果均方根误差为±0.018,可见IABC-LSSVR模型预测效果最佳,也说明本文改进的ABC比标准ABC的参数寻优效果更好。由图 3可知,IABC-LSSVR模型预测的变形量曲线与观测变形值曲线更为吻合,说明IABC-LSSVR模型比ABC-LSSVR模型以及PSO-GM-ARMA模型更能反映变形的趋势。
5 结语针对标准ABC的不足之处,本文提出一种正反双蜂群交叉寻优算法来增加初始群体的多样性,并在搜索策略公式和概率选择公式中构造出2种不同的自适应函数来平衡标准ABC的勘探和开发能力,以此提出了IABC算法。利用IABC与LSSVR进行有效结合,从而使得LSSVR具有更优的预测性能。通过实例证明,本文改进的ABC算法与标准ABC算法相比,增加了种群的多样性,平衡了算法的勘探和开发能力,提高了收敛精度。且本文构建的IABC-LSSVR模型较ABC-LSSVR模型以及PSO-GM-ARMA模型在预测精度上有明显的优势,在变形监测方面具有一定的应用价值。
| [1] |
Vapnik V N. The Nature of Statistical Learning Theory[M]. New York: Springer, 1995
(  0) 0) |
| [2] |
谢宏, 魏江平, 刘鹤立. 短期负荷预测中支持向量机模型的参数选取和优化方法[J]. 中国电机工程学报, 2006, 26(22): 17-22 (Xie Hong, Wei Jiangping, Liu Heli. Parameter Selection and Optimization Method of SVM Model for Short-Term Load Forecasting[J]. Proceedings of the CSEE, 2006, 26(22): 17-22 DOI:10.3321/j.issn:0258-8013.2006.22.004)
(  0) 0) |
| [3] |
高雷阜, 高晶, 赵世杰. 人工蜂群算法优化SVR的预测模型[J]. 计算机工程与应用, 2016, 52(11): 55-59 (Gao Leifu, Gao Jing, Zhao Shijie. Forecast Model of SVR Optimized by Artificial Bee Colony Algorithm[J]. Computer Engineering and Applications, 2016, 52(11): 55-59 DOI:10.3778/j.issn.1002-8331.1407-0435)
(  0) 0) |
| [4] |
林凯, 陈国初, 张鑫. 多交互式人工蜂群算法及其收敛性分析[J]. 计算机应用, 2017, 37(3): 760-765 (Lin Kai, Chen Guochu, Zhang Xin. Multiple Interactive Artificial Bee Colony Algorithm and Its Convergence Analysis[J]. Journal of Computer Applications, 2017, 37(3): 760-765)
(  0) 0) |
| [5] |
任超, 梁月吉, 庞光锋, 等. 基于灰色最小二乘支持向量机的大坝变形预测[J]. 大地测量与地球动力学, 2015, 35(4): 608-612 (Ren Chao, Liang Yueji, Pang Guangfeng, et al. Dam Deformation Prediction Based on Grey Least Square Support Vector Machines[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 608-612)
(  0) 0) |
| [6] |
王奉伟, 周世健, 周清, 等. 局部均值分解与支持向量回归的大坝变形预测[J]. 测绘科学, 2016, 41(10): 132-135 (Wang Fengwei, Zhou Shijian, Zhou Qing, et al. Forecasting Model of Dam Deformation Based on LMD-SVR Method[J]. Science of Surveying and Mapping, 2016, 41(10): 132-135)
(  0) 0) |
| [7] |
韩建权, 毛力, 周长喜. 基于改进局部搜索策略的人工蜂群算法[J]. 计算机科学与探索, 2015, 9(6): 761-767 (Han Jianquan, Mao Li, Zhou Changxi. Artificial Bee Colony Algorithm Based on Improved Local Search Strategy[J]. Journal of Frontiers Science and of Computer Science and Technology, 2015, 9(6): 761-767)
(  0) 0) |
| [8] |
秦全德, 程适, 李丽, 等. 人工蜂群算法研究综述[J]. 智能系统学报, 2014, 9(2): 127-135 (Qin Quande, Cheng Shi, Li Li, et al. Artificial Bee Colony Algorithm: A Survey[J]. CAAI Transactions on Intelligent Systems, 2014, 9(2): 127-135)
(  0) 0) |
| [9] |
Huapt R, Huapt S. Practical Genetic Algorithm[M]. New Jersey: John Wiley & Sons, 2004
(  0) 0) |
| [10] |
Zhu G P, Kwong S. Gbest-Guided Artificial Bee Colony Algorithm for Numerical Function Optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166-3173 DOI:10.1016/j.amc.2010.08.049
(  0) 0) |
| [11] |
王显鹏, 黄声享, 李冠青. 基于粒子群算法的组合模型在变形分析中的应用[J]. 测绘工程, 2017, 26(1): 73-76 (Wang Xianpeng, Huang Shengxiang, Li Guanqing. Application of Combined Model Based on Particle Swarm Optimization in Deformation Analysis[J]. Engineering of Surveying and Mapping, 2017, 26(1): 73-76)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


