2. 武汉地震工程研究院有限公司,武汉市洪山侧路40号,430071
预测饱和砂(粉)土在地震作用下是否会发生液化是工程地基抗震设计中的重要环节之一。对砂土液化的评估包括3方面的内容:1)评判土层有无液化的可能性;2)确定临界液化深度;3)评价场地液化等级。目前,国内通常采用各行业既有抗震设计规范中推荐的经验公式(以下简称“规范法”)评估场地饱和砂(粉)土的液化情况,其最大适用深度为地面下20 m。然而,对于地层中广泛分布着深厚砂性土的沿海(江)地区,时常会有埋深跨越20 m的饱和砂层,故实际工程中亟需找到一种液化判别方法作为“规范法”的补充。
深层液化判别方法大致可分为室内试验和现场测试的经验方法2种[1]。黄雅虹等[2]采用前者对港珠澳特大桥覆盖层43 m深度范围内的砂土层进行液化判别,获得了明确的结果,但试验过程相对复杂,难以在一般工程中实现。后者以Dorby等[3]提出的以剪切波速为指标的液化判别法应用最为普遍,如石兆吉等[4]收集唐山地震现场液化资料建立了饱和砂(粉)土的“临界剪切波速”经验判别式;姚运生等[5]利用该经验公式对荆沙长江公路大桥主桥墩基15 m以下的液化情况进行探讨,效果良好。由于该经验公式是基于天津的地震资料建立的,能否推广到全国其他地区尚无定论[6]。因此,本文拟从Dorby等推导的原始液化判别式入手,结合石兆吉[7]根据国内外大量三轴试验液化结果确定的经验参数,尝试对“规范法”适用范围以外的饱和砂土液化情况及液化深度判别进行探讨,为工程场地的抗震设计和液化防治措施提供一定的参考依据。
1 判别原理利用剪切波速法作为液化判别手段的理论基础是Seed等[8]提出的评估饱和砂土液化势的简化方法。汪闻韶[9]在此基础上推导出临界液化剪切波速表达式:
| $ {V_{{\rm{cr}}}} = \sqrt {\frac{{0.65{\alpha _{\max }}h{r_d}}}{{{\gamma _{{\rm{cr}}}}{{(\frac{G}{{{G_{\max }}}})}_{{\gamma _{{\rm{cr}}}}}}}}} $ | (1) |
式中,αmax为地表水平最大加速度,单位m/s2;h为土层埋深,单位m;rd为随深度的应力折减系数,按Liao等[10]的建议取值;γcr为临界剪应变;(G/Gmax)γcr为临界剪应变γcr对应的临界剪应变模量。
由式(1)可以看出,求得临界剪切波速Vcr的关键参数是临界剪应变γcr和对应的临界剪应变模量。石兆吉[7]根据室内动三轴试验和地震现场资料结果确定,γcr取0.02%是适宜的,与此对应的砂土和粉土的临界剪应变模量分别取0.012 5和0.028 08。将上述取值代入式(1),得到饱和砂(粉)土的临界剪切波速计算公式为:
| $ 砂土\quad {V_{{\rm{cr}}}} = \sqrt {2.6 \times {{10}^5}{\alpha _{{\rm{max}}}}h{r_d}} $ | (2) |
| $ 粉土\quad {V_{{\rm{cr}}}} = \sqrt {178\;063{\alpha _{{\rm{max}}}}h{r_d}} $ | (3) |
在某概率水准下,当场地实测剪切波速V≥Vcr时,即认为该深度处的饱和砂土和粉土不用考虑砂土液化的问题。
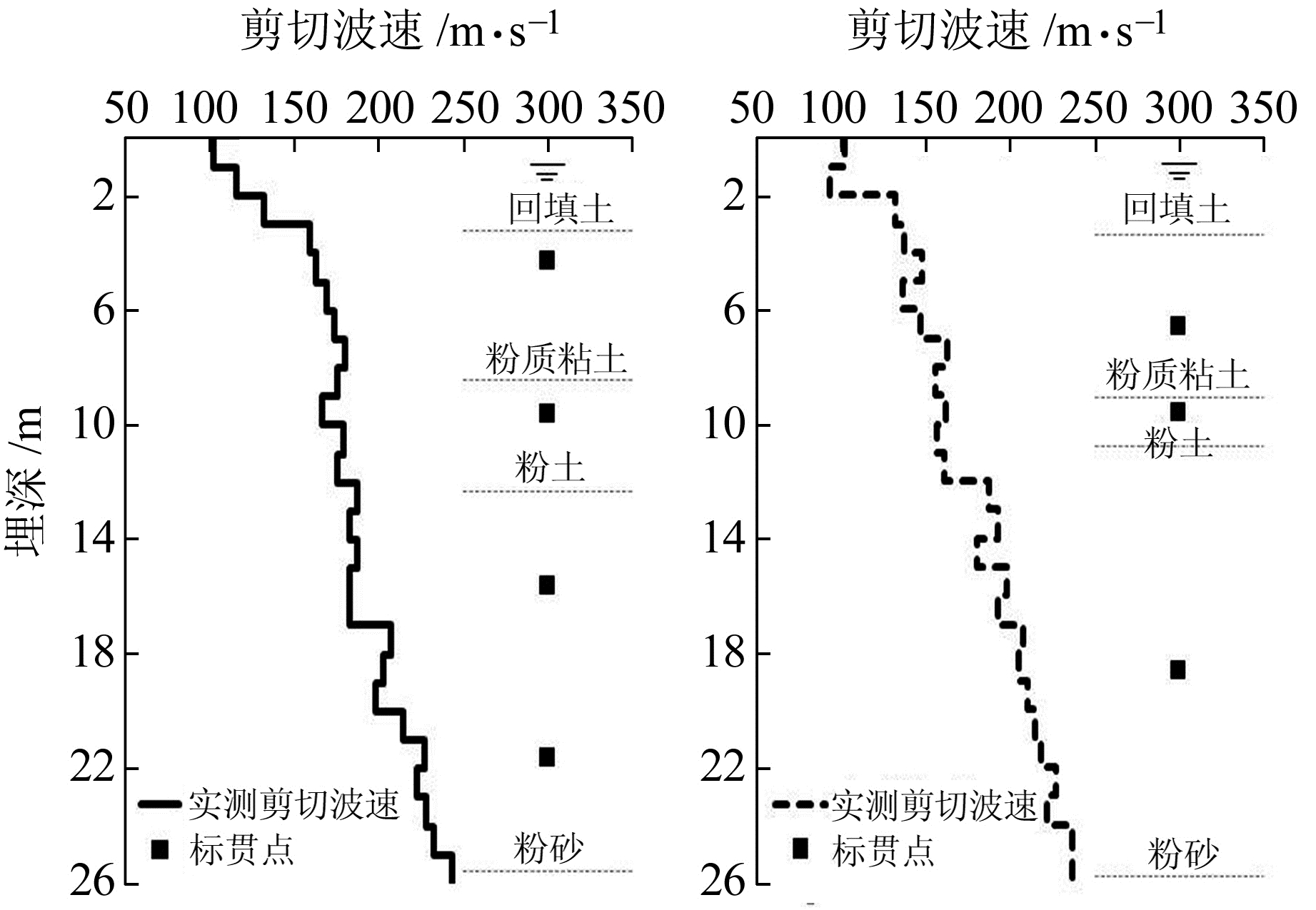
2 实例分析 2.1 工程概况武汉某建设工程场地位于汉口解放南路与新马路交汇处,场地地貌单元属长江Ⅰ级阶地,地形平坦,主要沉积地层为河流相土层。结合2个勘探钻孔(ZK1和ZK2)的剖面资料及室内土工试验,得到场地土层分布情况和参数见表 1,土体原位测试结果见图 1。
|
|
表 1 钻孔剖面资料 Tab. 1 Data of drillig profile |
|
图 1 ZK1和ZK2孔原位测试结果 Fig. 1 In-situ testing results of ZK1 and ZK2 borehole |
本文采用《建筑抗震设计规范》(GB50011-2010)[11]推荐的经验公式对饱和粉土、砂土层进行液化判别。若临界标贯值Ncr≥实测标贯值N,判别为液化,否则为不液化。
根据工程场地设计地震动参数的计算结果(表 2),在超越概率50 a 10%地震作用下,场地抗震设防烈度相当于Ⅵ度。饱和粉土、砂土可不考虑液化问题,超越概率为50 a 2%和100 a 2%地震作用下的判别结果见表 2。
|
|
表 2 地震反应分析计算结果 Tab. 2 The calculation results of seismic response analysis |
表 3的液化判别结果表明,场地内18.6 m范围内饱和粉土及粉砂层在50 a 2%和100 a 2%概率水准的地震作用下计算得到的临界标贯值Ncr均大于实测标贯值N,会发生液化破坏现象。
|
|
表 3 标准贯入试验判别砂土液化成果 Tab. 3 Differentiating results of liquefaction by standard penetration test |
场地勘探钻孔揭露,场地内饱和粉砂层的层底埋深为25.60~25.80 m。受场地实际标准贯入度深度及数量的影响,“规范法”仅能对埋深小于18.6 m的饱和砂层进行液化评估。因此,场地的液化结论会面临2个问题:1)若保守地认为20 m以下的该砂层同样会发生液化,按该层层底埋深确定抗液化措施及处理深度,则可能增加施工成本;2)若按照“规范法”的适用范围,将场地临界液化深度确定为20 m,则有可能高估20 m以下土层的抗液化能力,使工程存在较大的安全隐患。
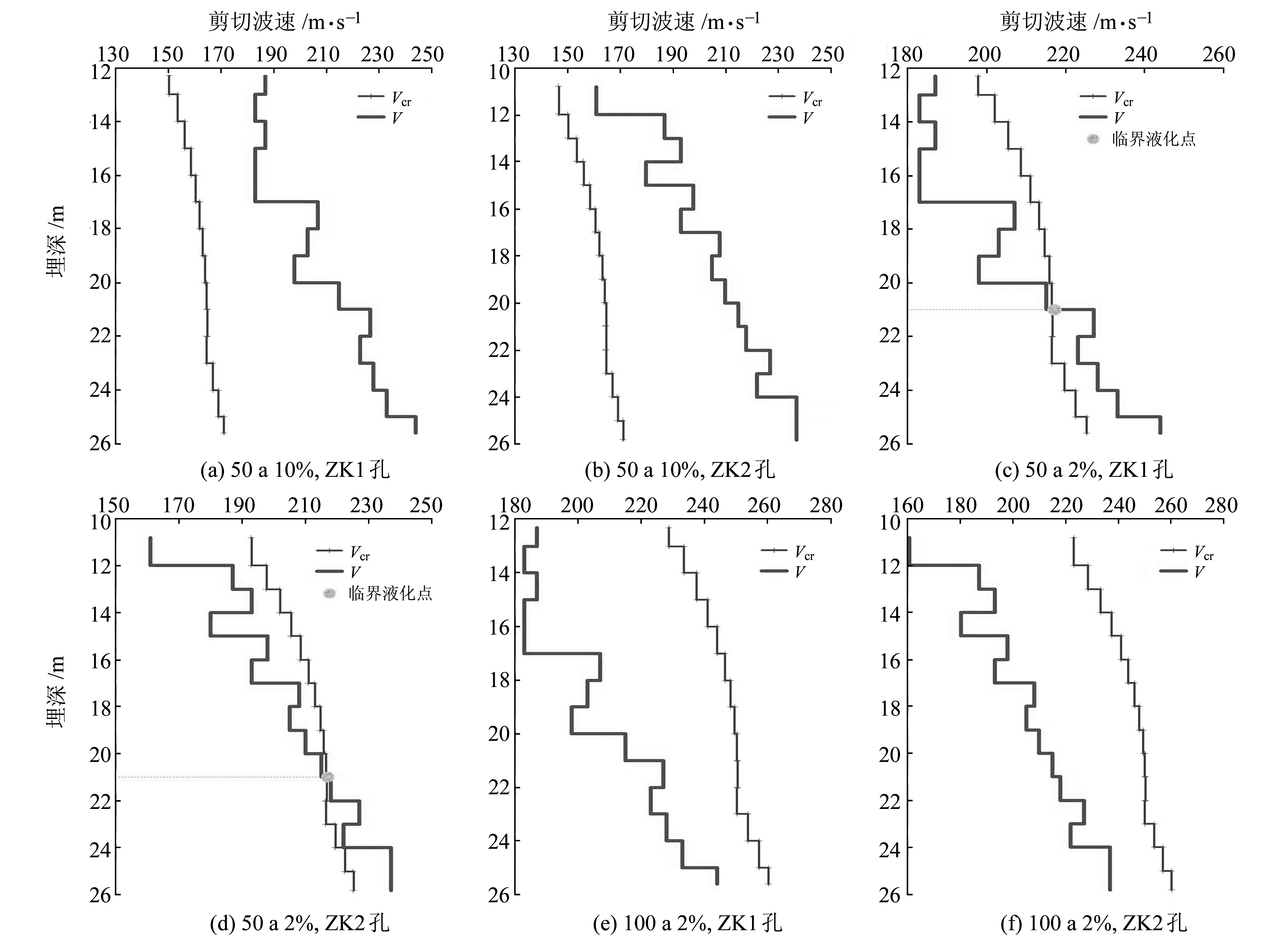
2.2.2 基于剪切波速法的液化判别结果将表 2中地表水平最大加速度αmax代入式(2)和式(3), 计算得出50 a 10%、50 a 2%和100 a 2% 3种概率水准下场地不同深度处饱和砂土层的临界剪切波速值Vcr。随后在上述3种概率水准的地震作用下,将ZK1和ZK2饱和粉砂层沿土层深度分布的实测剪切波速V曲线与临界剪切波速Vcr曲线绘于图 2。
|
图 2 V曲线与Vcr曲线比较 Fig. 2 Comparison between V and Vcr curve |
通过对比3种概率水准下V与Vcr的大小可知,在50 a 10%的地震作用下,饱和粉砂层的V≥Vcr,表明发生液化的可能性较小;在50 a 2%的地震作用下,2条曲线相交于埋深21 m处,该深度以上V>Vcr,表明饱和粉砂层不会发生液化,该深度以下V<Vcr,表明会发生液化,因此场地的临界液化范围可以确定在21 m左右;在100 a 2%的地震作用下,饱和粉砂层的V≤Vcr,表明饱和粉砂层均会发生液化破坏。
上述结果在埋深18.6 m范围内与“规范法”对于饱和粉砂层的液化判别结果完全一致,说明§1推导出的公式是适用的。对于18.6 m以下的液化判别结果,利用另一个具有代表性的液化判别方法——抗液化剪应力法进行验证。
2.2.3 与抗液化剪应力法结果对比抗液化剪应力法通过在室内采用动三轴试验模拟地震发生时的应力状态进行液化试验,测定发生液化时所需的抗液化剪应力τd。对于要判别的土层,求得沿土层深度分布的等效平均剪应力τc曲线和τd曲线,绘于同一图中,通过对比τd与τc的大小判断土层是否会液化。
1) 确定τc。根据场地设计地震动参数的计算结果(表 2),代入式(4)可计算出不同概率水准地震作用时的τc:
| $ {\tau _c} = 0.65\frac{{{\alpha _{{\rm{max}}}}}}{g}{\sigma _v}{r_d} $ | (4) |
式中,g为重力加速度,单位m/s2;σv为上覆初始总应力,单位kPa。
2) 确定τd。天然埋藏状态下土层的抗液化剪应力τd由式(5)确定:
| $ {\tau _d} = {C_r}\sigma {' _v}\frac{{{\sigma _d}}}{{2\sigma {' _0}}} $ | (5) |
式中,Cr为修正系数;σ'v为土层的有效覆盖压力,单位kPa;σ'd/2σ'0为抗液化剪应力比,由振动三轴试验确定。
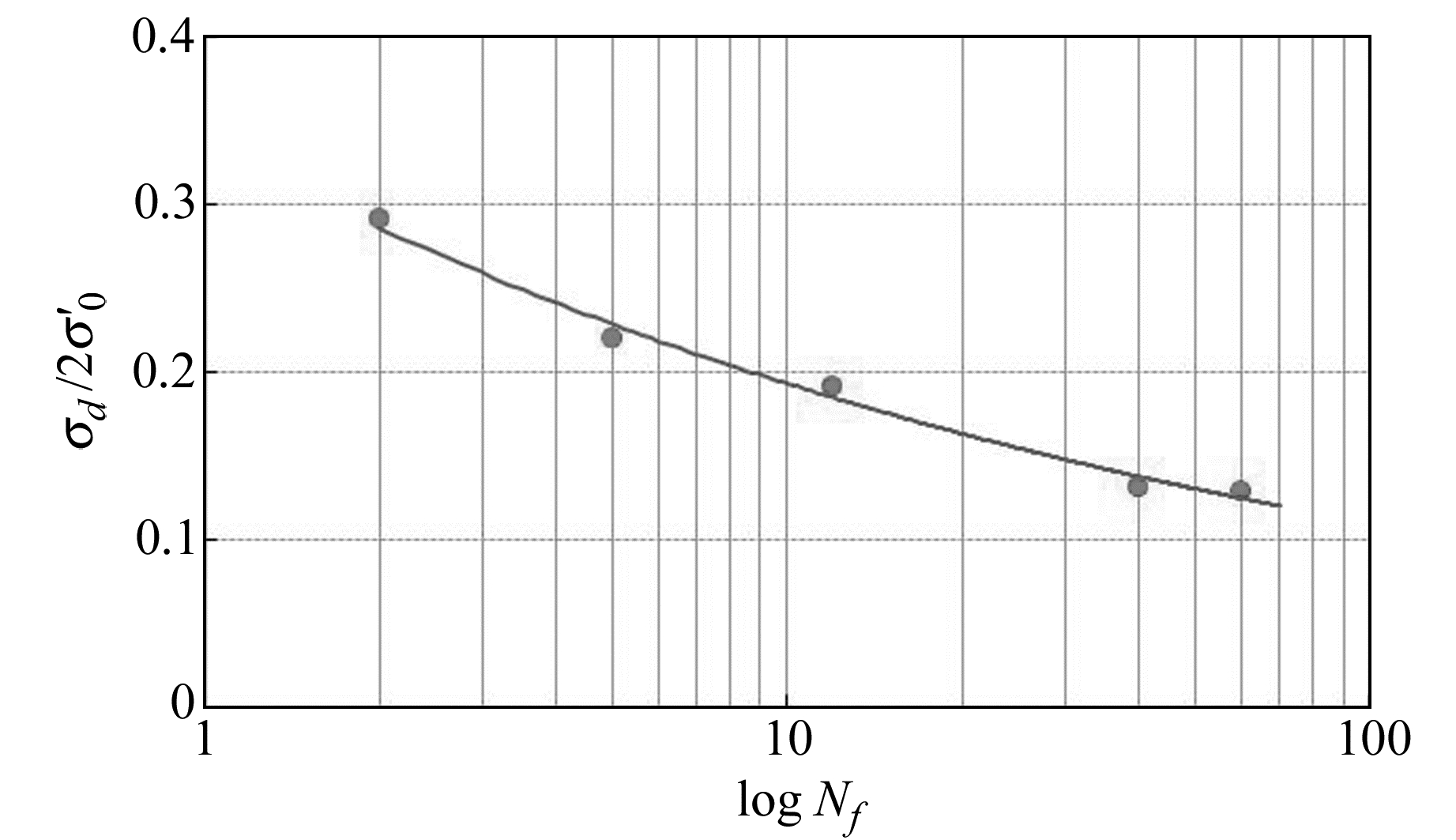
取饱和粉砂层进行重塑土试样的振动三轴液化试验。整个试验严格按《土工试验规程SDS01-79(下册)》[12]所规定的饱和砂土振动三轴试验规程进行。试验按固结压力σc=200 kPa,假定超固结比Kc=1,及以双幅轴向应变达到5%为液化标准,得到了给定不同循环应力作用下引起饱和粉砂发生液化时的循环次数Nf;然后在抗液化强度曲线上找出相应的抗液化应力比σ'd/2σ'0。以破坏循环次数Nf为横坐标,抗液化应力比σ'd/2σ'0为纵坐标,绘制代表深度处饱和粉砂动剪切应力比σ'd/2σ'0与破坏循环振次Nf的液化强度曲线(图 3)。
|
图 3 σd/2σ'0和logNf关系曲线 Fig. 3 Relationship of σd/2σ'0 versus logNf |
结合表 4及式(5)可得出不同概率水准作用下饱和粉砂层的抗液化剪应力τd。
|
|
表 4 不同概率水准下粉砂层抗液化剪应力比 Tab. 4 The stress ratio causing liquefaction of silt under different probability level |
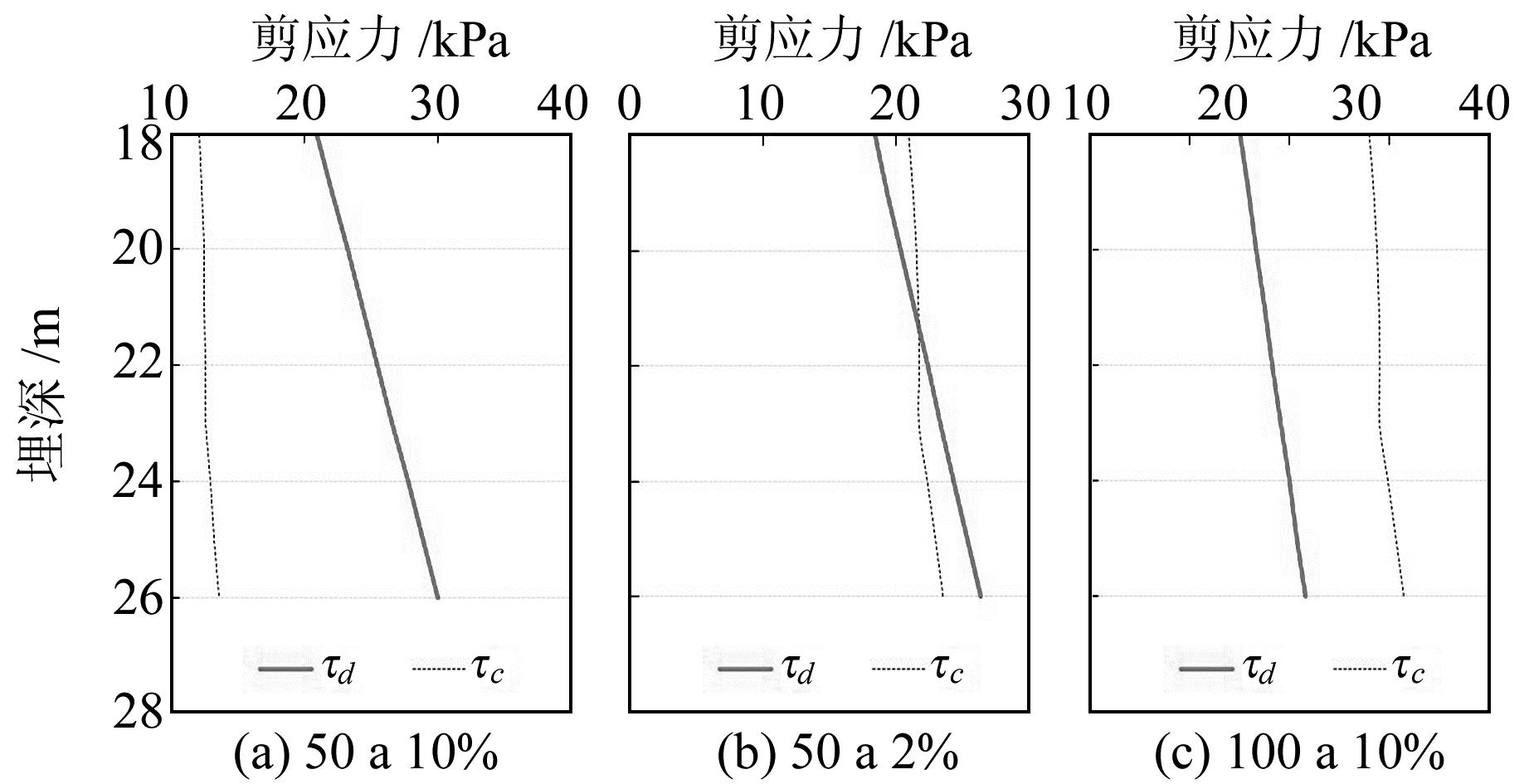
3) τc与τd的比较。将计算得到的τc与τd进行比较,若τc≥τd则可能发生液化,否则不会发生液化。根据液化判别结果,确定ZK1孔、ZK2孔粉砂层可能发生的液化区域。
由表 5、6和图 4、5可以看出,概率水准为50 a 10%时,τd≥τc,因此不会发生液化;概率水准为50 a 2%时,2条曲线出现交点,由于埋深22 m以上区域的τc≥τd,故临界液化深度可保守定为22 m;概率水准为100 a 2%时,τd≤τc,说明会发生液化。
|
|
表 5 ZK1不同概率水准20 m以下的τd与τc Tab. 5 τd and τc below 20 m under different probability level of ZK1 borehole |
|
|
表 6 ZK2不同概率水准20 m以下的τd与τc Tab. 6 τd and τc below 20 m under different probability level of ZK1 borehole |
|
图 4 ZK1孔粉砂层液化区域 Fig. 4 The silt layer liquefaction region of ZK1 borehole |
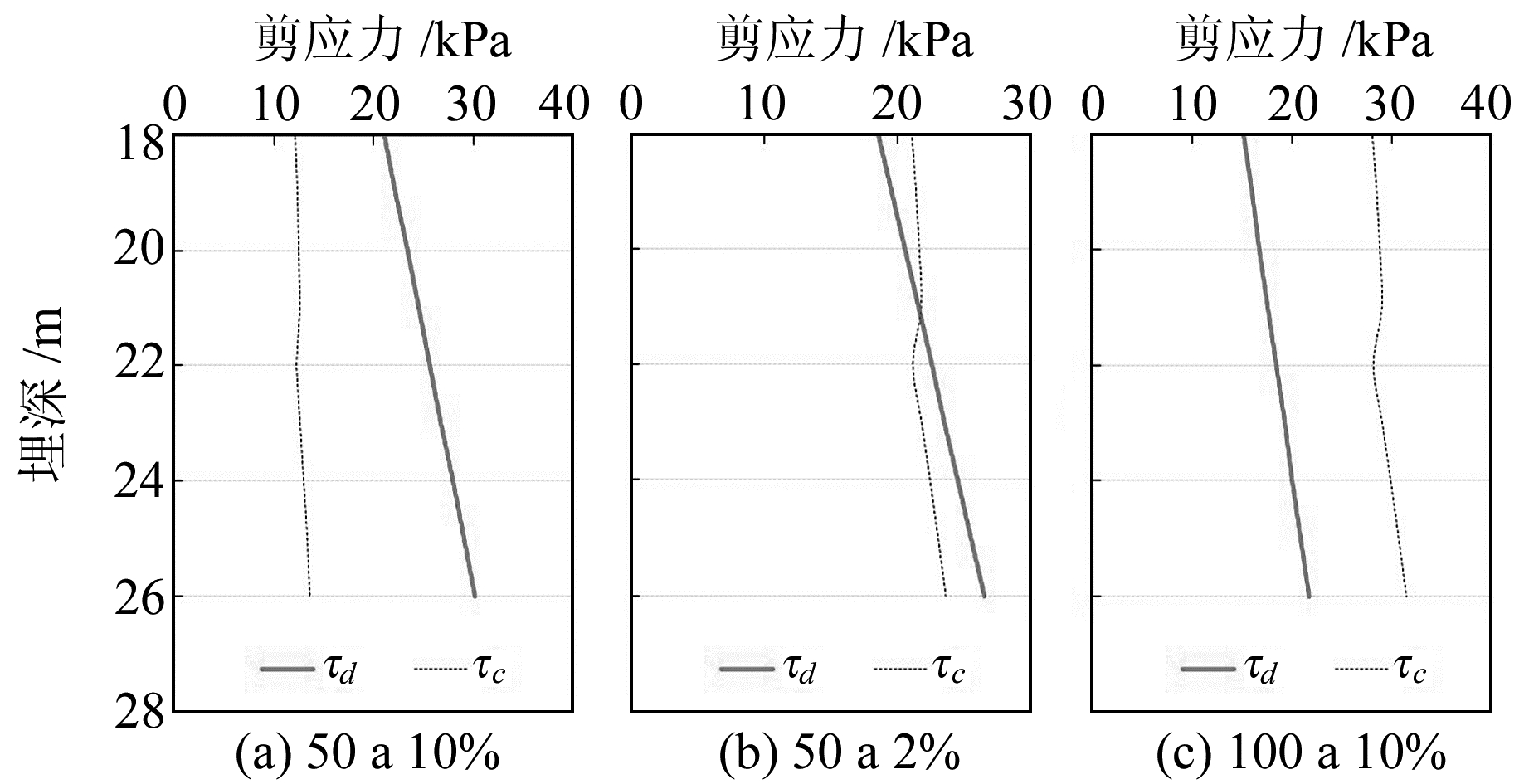
|
图 5 ZK2孔粉砂层液化区域 Fig. 5 The silt layer liquefaction region of ZK2 borehole |
通过对比剪切波速法和抗液化剪应力法的判别结果可知,无论是对不同概率水准的地震作用下场地饱和粉砂层的液化可能性判别,亦或是场地临界液化深度的确定,2种方法的判别结果均吻合较好。
3 结语本文以武汉某建设工程为例,利用临界剪切波速判别公式,确定场地深层饱和砂土层在不同概率水准的地震作用下是否会发生液化,通过与“规范法”及抗液化剪应力法的判别结果对比,得到以下结论:
1) 对埋深不超过20 m的饱和砂土层,利用剪切波速法与利用“规范法”进行液化判别的结果完全一致。
2) 对超出“规范法”适用范围的饱和砂土层,利用剪切波速法与抗液化剪应力法进行液化判别及确定临界液化深度的结果基本吻合。
综上所述,在目前尚无关于深层土液化判别的统一方法前,本文推导出的以剪切波速为指标的判别式可以成为“规范法”的补充,用于辅助评估场地深层饱和砂土地基的液化情况,为工程确定抗液化措施及处理深度提供理论依据。此外,剪切波速作为建筑场地类别评价的必要指标,用作场地液化评估无需增加额外工作量,并且相比其他现场测试方法(如标贯试验),剪切波测试具有连续性好、离散性小、可重复、快速又经济等优点,因此,该方法在沿海(江)区域工程中具有较强的实用性和良好的应用前景。
| [1] |
任红梅, 吕西林, 李培振. 饱和砂土液化研究进展[J]. 地震工程与工程振动, 2007, 27(6): 166-175 (Ren Hongmei, Lü Xilin, Li Peizhen. Advances in Liquefaction Research on Saturated Soils[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(6): 166-175 DOI:10.3969/j.issn.1000-1301.2007.06.026)
(  0) 0) |
| [2] |
黄雅虹, 吕悦军, 荣棉水, 等. 关于深层砂土液化判定方法的探讨——以港珠澳特大桥水下隧道工程场地为例[J]. 岩石力学与工程学报, 2012, 31(4): 856-864 (Huang Yahong, Lü Yuejun, Rong Mianshui, et al. Study of Evaluation Method of Liquefaction for Sandy Soil in Deep Layer:Taking Undersea Tunnel Site of Hongkong-Zhuhai-Macao Great Bridge for Example[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(4): 856-864)
(  0) 0) |
| [3] |
Dobry R, Ladd R S, Yokel F Y, et al. Prediction of Pore Water Ptessure Build up and Liquefacting of Sands during Earthquakes by the Cyclic Strain Method[C]. NBS Building Science Series 138, National Bureau of Standards, US Department of Commerce, 1982
(  0) 0) |
| [4] |
石兆吉, 郁寿松, 丰万玲. 土壤液化势的剪切波速判别法[J]. 岩土工程学报, 1993, 15(1): 74-80 (Shi Zhaoji, Yu Shousong, Feng Wanling. Shear Wave Velocity Method to Determine Soil Liquefaction Potential[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(1): 74-80 DOI:10.3321/j.issn:1000-4548.1993.01.011)
(  0) 0) |
| [5] |
姚运生, 黄江, 罗登贵, 等. 荆沙长江公路大桥主桥墩基地震液化研究[J]. 水文地质工程地质, 2001, 28(1): 42-45 (Yao Yunsheng, Huang Jiang, Luo Denggui, et al. Study on the Seismic Liquefaction of the Main Pier Base of the Yangtze River Highway Bridge[J]. Hydrogeology and Engineering Geology, 2001, 28(1): 42-45 DOI:10.3969/j.issn.1000-3665.2001.01.012)
(  0) 0) |
| [6] |
陈国兴, 张克绪, 谢君斐. 以剪切波速为指标的液化判别方法及其适用性[J]. 哈尔滨建筑大学学报, 1996, 29(1): 97-103 (Chen Guoxing, Zhang Kexu, Xie Junfei. The Method of Liquefaction Discrimination Based on Shear Wave Velocity and Its Applicability[J]. Journal of Harbin University of Archiecture and Enginerring, 1996, 29(1): 97-103)
(  0) 0) |
| [7] |
石兆吉. 判别水平土层液化势的剪切波速法[J]. 水文地质工程地质, 1986(4): 9-13 (Shi Zhaoji. Shear Wave Velocity Method for Determining the Liquefaction Potential of Horizontal Soil Layer[J]. Hydrogeology and Engineering Geology, 1986(4): 9-13)
(  0) 0) |
| [8] |
Seed H B, Idriss I M. Sinplified Procedure for Evaluating Soil Liquefaction Potential[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1971, 97(9): 1249-1273
(  0) 0) |
| [9] |
汪闻韶. 剪切波速在评估地基饱和砂层地震液化可能性中的应用[J]. 岩土工程学报, 2001, 23(6): 655-658 (Wang Wenshao. Utilization of Shear Wave Velocity in Assessment of Liquefaction Potential of Saturated Sand under Level Ground during Earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(6): 655-658 DOI:10.3321/j.issn:1000-4548.2001.06.001)
(  0) 0) |
| [10] |
Liao S S C, Whitman R V. Overburden Correction Factors for SPT in Sands[J]. Journal of the Geontechnical Engineering Divisions, ASCE, 1986, 112(3): 373-377 DOI:10.1061/(ASCE)0733-9410(1986)112:3(373)
(  0) 0) |
| [11] |
中华人民共和国住房和城乡建设部. GB 50011-2010建筑抗震设计规范[S].北京: 中国建筑工业出版社, 2010 (Ministry of Housing and Urban-Rural Development of People's Republic of China. GB 50011-2010 Code for Seismic Design of Buildings[S]. Beijing: China Building Industry Press, 2010)
(  0) 0) |
| [12] |
中华人民共和国水利部, 电力工业部. SDS01-79土工试验规程(下册)[S].北京: 水利出版社, 1981 (Ministry of Water Resources, Ministry of Electric Power Industry of People's Republic of China. SDS01-79 Geotechnical Test Procedures[S]. Beijing: Water Conservancy Press, 1981)
(  0) 0) |
| [13] |
胡庆, 李恒, 张祎. 基于动三轴试验和土层地震反应对地震液化的判别[J]. 大地测量与地球动力学, 2017, 37(5): 531-535 (Hu Qing, Li Heng, Zhang Yi. Liquefaction Evaluation Based on Dynamic Triaxial Test and Soil Seismic Response[J]. Journal of Geodesy and Geodynamics, 2017, 37(5): 531-535)
(  0) 0) |
2. Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Road, Wuhan 430071, China
 2019, Vol. 39
2019, Vol. 39

