2. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,410079
精密大地水准面模型是高程基准现代化的关键基础设施。高精度大地水准面模型与GNSS测定的大地高结合可以快速获得精密海拔高程。CQG60和CQG80为我国第一代似大地水准面模型。此后,武汉大学、西安测绘研究所和中国科学院测量与地球物理研究所先后提出了WDM、WZD系列重力场模型,为精化水准面奠定了基础[1-2]。2000年提出的CNGG2000和CQG2000似大地水准面模型利用约40万个地面重力数据、多类卫星测高海洋重力异常数据,精度较CQG80提高1个数量级以上[3-4]。当前我国最新重力似大地水准面模型为CNGG2011,全国平均精度为±0.126 m,东、西部精度分别为±0.071 m和±0.138 m,与美国等国的似大地水准面精度相当[5]。2014年来,广西、江苏等研制了精度优于±0.04 m的似大地水准面模型[6-7],长沙等市级似大地水准面模型精度则优于±0.01 m[8-9]。
2007年湖南省利用近3万个地面重力观测资料,基于EGM96全球重力场模型,采用Molodensky原理移去-恢复获得重力似大地水准面,将其拟合适配于省内559个A、B、C级GPS/水准控制点,取得了分辨率2.5′×2.5′的似大地水准面模型(以下简称2007模型),通过27个检核点获得其外符合检测精度为±0.043 m[10-11]。该模型在湖南地区1:5 000、1:10 000比例尺、市级似大地水准面建设等重大工程中发挥了显著的作用。后续应用研究表明,该模型在湘北平原地区的精度优于±2 cm;湘中丘陵区为±4 cm,山区为±6 cm;在局部地区存在粗差,最大值为15.6 cm和-18.5 cm。目前,湖南地区的重力卫星和地面数据、重力场模型、GNSS/水准控制数据更加丰富,基于Stokes框架的Stokes-Helmert边值计算[12]、GNSS/水准拟合插值技术取得重要突破,为进一步提高似大地水准面模型的精度和现势性奠定了基础。本文首先介绍基础数据,然后基于Stokes-Helmert凝集法计算重力似大地水准面,再利用球冠谐调和分析将重力似大地水准面校准至我国高程基准,获得湖南省似大地水准面2017模型(HNGG2017)。最后,结合2007模型和GNSS/水准控制点数据,对精度进行分析。
1 Stokes-Helmert凝集法Stokes-Helmert方法是以Stokes理论为框架,采用Helmert地形补偿模式,求解大地水准面外部扰动位的边值:
| $ \left\{ \begin{array}{l} {\nabla ^2}{T^h} = 0,在\;{S_g}\;外部空间\\ \left| {\nabla \left( {U + {T^h} + \delta V} \right)} \right| = g,在\;{S_t}\;上\\ U + {T^h} + \delta V = {W_0},在\;{S_g}\;上\\ {T^h} \sim O\left( {\frac{1}{r}} \right),r \to \infty \end{array} \right. $ | (1) |
式中,Th为待求解的Helmert重力场扰动位函数,U为正常重力位,Sg为大地水准面,St为地形表面,g为重力测量值,W0为已知Sg上的重力位常数。设Vt和Vc分别为地形和凝集层引力位,则式(1)中的这2种引力位之差为:
| $ \delta V = {V^t} - {V^c} $ | (2) |
式中,δV即为对大地水准的第一间接影响。式(1)中的第2式是一个非线性边值条件,其球近似线性化形式为:
| $ \frac{{\partial {T^h}}}{{\partial r}}\left| {_P} \right. + \frac{2}{{{r_Q}}}T_{{P_g}}^h = - \Delta {g^h} $ | (3) |
式中,
| $ \frac{{\partial {T^h}}}{{\partial r}} = - \left( {{g_P} - {\gamma _P}} \right) - \delta A $ | (4) |
式中,Δgh为Helmert重力异常:
| $ \begin{array}{l} \Delta {g^h} = {g_P} - {\gamma _Q} + F + \delta A + \frac{2}{{{r_Q}}}\delta {V_{{P_g}}} = \\ \Delta {g_P} + \delta A + \frac{2}{{{r_Q}}}\delta {V_{{P_g}}} \end{array} $ | (5) |
式(1)是一个Stokes双边值问题,涉及2个边界面St和Sg。式(5)中下标P、Q、Pg分别表示地面点及其在正常椭球面上的法向投影点和大地水准面上的垂向投影点,γ为正常重力,F为空间改正,Δgp为空间异常,δA为地形对地面重力的直接影响:
| $ \delta A = \frac{{\partial \delta V}}{{\partial r}}\left| {_P} \right. = {A^t} - {A^c} $ | (6) |
式中,At和Ac为地形体和凝集层对P点的引力。式(5)中的最后一项为对Sg上Δg的第二间接地形影响,用δS表示为:
| $ \delta S = \frac{2}{{{r_Q}}}\delta {V_{{P_g}}} $ | (7) |
式(1)中的第3式为边界面Sg上解算的扰动位函数(Th+δV)Pg加正常位UPg,应等于W0的边值条件。将UPg在点Q上作Taylor级数展开,略去二次及高阶项,则有UPg=UQ-γQN,N为大地水准面高,即得到布隆斯公式:
| $ N = \frac{1}{{{r_Q}}}\left( {{T^h} + \delta V} \right)\left| {_{{P_g}}} \right. $ | (8) |
式(8)即为用Stokes-Helmert方法计算的大地水准面高。结合式(3)和式(5),由Stokes积分可计算Helmert重力场的高程异常:
| $ {\zeta ^h} = \frac{R}{{4{{\rm{ \mathsf{ π} }}}\gamma }}\iint\limits_\sigma {\Delta {g^h}S\left( {r,\psi } \right){\text{d}}\sigma } $ | (9) |
式中,R为地球平均半径,r为计算点的地心距,ψ为计算点与流动积分点间的地心角距,σ为单位球面。则高程异常为:
| $ \zeta = {\zeta ^h} + \frac{{\delta V}}{\gamma } $ | (10) |
式中,δV=δW=Vt-Vc,为地面重力位变化,即地面地形引力位与凝集层引力位之差。
2 数据收集 2.1 重力地面数据HNGG2017计算时收集了108°~115°E、24°~31°N范围内的重力地面观测数据,共计69 968个。湖南省中东部地面重力数据较密集,东北部洞庭湖区、北部和西部山区、西南部和东南部东江湖地区密度相对较低。
2.2 GNSS/水准控制数据GNSS/水准数据主要用于似大地水准面的计算和检核。本研究收集了4类GNSS/水准控制数据,共计783个,如图 1所示。

|
图 1 GNSS/水准控制点分布 Fig. 1 The distribution of GNSS/leveling points |
如图 1蓝点所示,GNSS/水准点包括湖南境内A、B、C级GNSS控制点(共计556个,其中建模点502个,检核点54个)、湖南省卫星导航定位基准站(47个,均为检核点)、国家基准站(12个,均为检核点)及数字城市控制点(168个,均为检核点)。
2.3 数字高程模型重力异常归算采用高分辨率DEM格网数据来计算相应地形和均衡改正。采用SRTM(shuttle radar topography mission)数据资料,分辨率为7.5"×7.5",可满足大地水准面精化要求,如图 1底图所示。
2.4 全球重力场模型全球重力场模型用于确定重力似大地水准面长波分量。本研究采用2 160阶次的EIGEN-6C4模型,与2007模型所用的EGM96模型相比,其数据源和模型阶数显著提升;与EGM2008模型相比,其现势性和理论阶方差精度更高[13]。
此外,基础数据还包括2007模型及相关科研数据、全省水准控制网成果、中国似大地水准面模型等,主要用于对比检核。
3 数值计算HNGG2017平均空间重力异常计算采用前文所述69 968个点重力数据,利用图 1所示部分GNSS/水准资料对重力似大地水准面进行校准。GNSS/水准资料共计502个,来自湖南省A、B、C级GNSS控制网成果,含大地高和正常高值。其中,106个A、B级控制点采用一等或二等水准联测,396个C级控制点采用三等水准联测,DEM数据地形最小、最大高程值为-132 m和2 527 m。格网空间重力异常计算采用点均衡重力异常,点重力值上的空间改正和布格改正均由重力点上的高程计算。地形和均衡改正由严格数值积分计算得出的7.5″×7.5″地形改正结果利用双三次内插方法计算。点均衡异常在内插其相应的2′×2′格网值时,利用张量曲率连续样条算法完成。
针对部分陆地上无实测重力值点的情况,利用WDM94地球模型填补。均衡重力异常的最小值和最大值分别为-62.512 mGal和22.611 mGal,该地区空间重力异常最小值和最大值分别为-131.642 mGal和111.619 mGal。采用2′×2′格网空间重力异常作为输入数据,以EIGEN-6C4为参考重力场,利用第二类Helmert凝集法计算重力似大地水准面。在利用第二类Helmert凝集法计算大地水准面中的各类地形位及地形引力的影响时,采用的公式均为考虑了地球曲率影响的严密球面积分公式,计算地形的直接和间接影响的积分半径均采用300 km。
502个GNSS/水准成果其标准差为±0.042 m,去掉系统偏移量-0.035 m后,最大值和最小值分别为0.121 m和-0.167 m。GNSS/水准似大地水准面与重力似大地水准面高存在着较大的垂向偏差和水平倾斜差异。本研究通过球冠谐分析来减小两者的差异,将重力似大地水准面统一到我国高程基准上。球冠谐分析选择较大的球冠半径θ0=0°40′。球冠北极纬度为27°30′00"N,经度为111°30′00"E,球冠谐系数展开的最大阶数为Nmax=10。最终获得空间分辨率2′×2′的GNSS/水准与拟合后似大地水准面高的统计结果如表 1(单位m)所示。
|
|
表 1 HNGG2017模型内符合精度统计结果 Tab. 1 The internal error statistics of HNGG2017 |
表 1中,GNSS/水准与拟合后似大地水准面的标准差为±0.031 m,偏差为0.000 m,最大值和最小值分别为0.105 m、-0.139 m。502个GNSS/水准控制点中,既有二等也有三等水准成果,而三等水准成果精度可能低于模型自身精度。为避免使用低精度控制点成果检验高精度模型而引入误差,仅利用106个A、B级点(均为二等水准成果)统计似大地水准面精度(结果为±0.022 m),作为GNSS重力似大地水准面模型内符合精度。
4 精度分析 4.1 外部检核选取未参与建模的控制点进行外部检核,包括4步:1)数据收集。外部检核点满足以下条件:未参与模型计算、分布均匀、GNSS成果不低于C级点水平、水准成果不低于二等水准标准。2)模型高程异常计算。根据坐标利用HNGG2017计算高程异常。3)控制点高程异常计算。根据控制点成果计算高程异常。4)对比分析。外部检核共选取77个点,包括10个A、B级控制点、43个HNCORS基准站、1个国家GNSS站和23个数字城市控制点,分布如图 1红点所示。外部检核点整体和分地形精度统计如表 2(单位m)所示。
|
|
表 2 HNGG2017模型外部检测点精度统计 Tab. 2 The external error statistics of HNGG2017 |
湖南省东、南、西三面环山,中部丘岗起伏,北部平原展开,为朝东北开口的不对称马蹄形地形。参照唐秋祥[10]的方法,将湖南省分为平原、丘陵和山地3类地形。外部检核误差分布如图 2所示。

|
图 2 HNGG2017模型外部检核误差空间分布 Fig. 2 The external error statistics map of HNGG2017 |
图 2中,湘东山丘、湘中丘陵、湘北平原检核误差主要在[-0.02, 0.02]m区间,说明平原和丘陵地区达到较高精度。湘西山地、湘南丘陵和山地误差绝对值主要在[0.02, 0.04]m范围,说明山地精度有一定下降。而湘西北、湘北壶瓶山地区误差最大,外部检核点(B级点1891)差异达-8 cm。该差异来源为控制点和HNGG2017模型误差,前者源于GNS S或水准测量。GNSS测量时,可能因天线高处理不当导致误差,且该地区高差较大,数据处理时对流层模型选择不当也会引起cm级误差。二等水准测量理论严密,可靠性较高,但存在起算数据有误等可能。同时,山地重力数据和边界控制点较少,在高差较大的区域可能引起一定误差,但因湖南地区为整体建模,出现局部精度突变的可能性小。因此,差异更有可能源自控制点数据。该区域将在下文进一步分析。
4.2 综合检核利用全部包含有大地高和正常高的控制点来对模型进行综合检核,点位空间分布如图 1蓝点所示。其中,98.9%的检核点的精度在[-0.1, 0.1]m区间,基本服从正态分布。综合检核点水准既有二等也有三等水准成果,统计精度优于±3.5 cm,说明HNGG2017精度较高。个别检测点差值超过0.1 m,剔除前后对应点位误差,结果如表 3(单位m)所示。
|
|
表 3 HNGG2017模型综合精度检测点统计 Tab. 3 The total error statistics for HNGG2017 |
774个综合检核点误差空间分布(剔除差值超过0.1 m的点)如图 3所示。
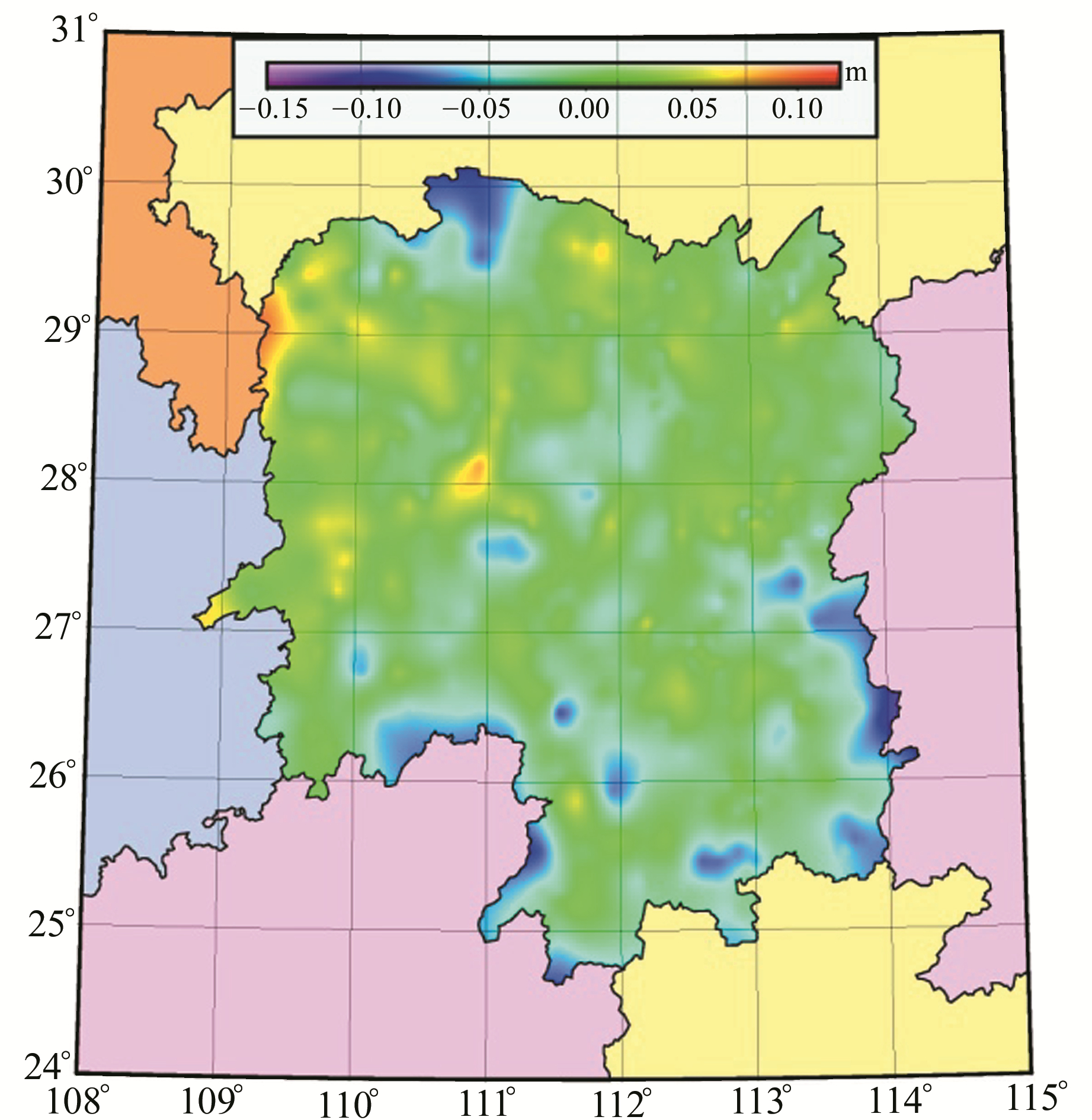
|
图 3 HNGG2017模型综合检测点精度分布 Fig. 3 The total error statistics of HNGG2017 |
结合图 3和表 3可知,综合检核点误差空间分布较均匀,大部分位于[-0.04, 0.04]m范围内,少数西北山区误差达+0.08 m以上,在北部、东南部地区误差达-0.08 m以上,符合山地精度低于平原、丘陵的空间分布特征。被剔除的点位主要位于永州双牌县茶林镇、常德石门县壶瓶山镇等。值得注意的是,与2017模型差异最大的综合检核点并非是外部检核中误差最大的B级GNSS点1891,而是C级GNSS控制点U004。上述地区控制点成果与HNGG2017之间差异较大。为进一步研究模型精度,本文将针对该类特征点位进行深入分析。
4.3 特征点检核特征点检核针对3类点进行实地测量检核:第1类点为2017与2007模型差异较大的点;第2类点为HNGG2017与控制点差异较大的点;第3类点为疑似存在系统性差异,难以采用上述方法获得结果的点。实地测量时,参照C级网技术规范执行,水准测量以最近的水准控制点为起算,参照二等水准规范实施。第1、2类特征点如表 4(单位m)所示。
|
|
表 4 HNGG2017模型特征点位误差分析结果 Tab. 4 The characteristic points error analysis of HNGG2017 |
点U155为第1类特征点,位于北部常德汉寿县。外业测量结果表明,GNSS和水准结果与原控制点成果一致。实测高程异常与HNGG2017高程异常差3.0 cm,与2007模型高程异常差16.0 cm,其原因可能是2007模型拟合过程存在问题或数据不足。
点U526为第1类特征点,位于西南永州江永县桃川镇。该点实测GNSS与原控制点成果一致,原控制点无正常高成果。该点实测高程异常与HNGG2017差9.4 cm,与2007模型差41.1 cm。江永地区位于湘桂边界,GNSS/水准数据不足,可能导致2007模型误差较大。2007模型相对更依赖GNSS/水准控制点的分布和密度,而HNGG2017更多依靠地面和卫星重力观测数据,在缺乏控制点条件下,能更真实地描述水准面特征。实测成果与HNGG2017相差9.4 cm的原因可能是水准测量距离过长(超过40 km)所致。
点U009为第2类特征点,位于湘西龙山县。实测高程异常与HNGG2017相差约1 cm,与控制点高程异常差6.5 cm。实测与控制点大地高差5.8 cm,实测控制点正常高差为0.7 cm,实测高程异常与HNGG2017高程异常差0.9 cm。2次GNSS测量差异达5.8 cm的原因可能是原控制点GNSS测量过程中,天线高量取有误或数据处理不当。
点U445为第2类特征点,位于西南部永州市双牌县茶林镇。该点实测高程异常与HNGG2017一致,仅差1.9 cm。实测与控制点大地高差16.5 cm,正常高差为0.6 cm。2期大地高差较大的原因应与点U009相似。
点U004为第2类特征点,位于北部常德市石门壶瓶山镇。由表 4知,该点实测结果均与原控制点一致,实测与HNGG2017高程异常差达17.3 cm。结合§3对该地区B级GNSS控制点1891的分析可知,该控制点与HNGG2017的差异可能来自2017模型、大地高、正常高3类误差。考虑到HNGG2017为统一建模,在外部检核精度达到2 cm的前提下基本不可能出现局部过大的偏差,而实测大地高结果又表明GNSS测量结果比较可靠,实测正常高表明该点与相邻控制点的高差基本一致。因此,考虑该地区水准起算数据可能存在问题。结合图 1可知,该地区控制点和模型之间的差异呈系统性,差异较大的点均分布于Ⅱ杨石线附近,相关控制点均处于Ⅱ杨石线上或以其作为起算数据。为进一步分析模型精度,设计第3类检核。本文选取U013点(差异2.7 cm)和U014点(差异8 cm),采用GNSS联测大地高差,水准联测正常高差,结果如表 5(单位m)所示。
|
|
表 5 U013-U014点高程异常差 Tab. 5 The height anomaly results between U013-U014 |
表 5中,U013-U014点实测与HNGG2017高程异常差一致,仅1.3 cm。其原因可能有:1)控制点正常高测量是按三等水准测量,而此次参照二等水准测量标准,精度更高;2)在壶瓶山区域,水准起算点可能存在偏差,有待于更多数据进行验证。总体而言,第3类特征点检核证明了HNGG2017的可靠性。
5 结语本研究采用近7万个湖南及邻近地区重力数据、美国SRTM7.5″×7.5″地形数据及502个A、B、C级GNSS/水准控制点数据,利用EIGEN-6C4全球重力场模型作参考重力场,采用Stokes-Helmert凝集法,计算了湖南省似大地水准面2017模型(HNGG2017)。精度分析表明,GNSS重力似大地水准面模型外部检核精度为±0.022 m;平原、山地和丘陵分别达到1 cm、2 cm和3.4 cm。与历史模型对比,新模型在常德汉寿、永州江永地区精度改善显著。实测结果表明,少量控制点存在较大误差。北部的壶瓶山地区水准成果起算点可能存在差异,且为系统性特征,有待于更多数据验证。
| [1] |
宁津生, 李建成, 晁定波, 等. WDM94 360阶地球重力场模型研究[J]. 武汉测绘科技大学学报, 1994, 19(4): 283-291 (Ning Jinsheng, Li Jiancheng, Chao Dingbo, et al. The Research of the Earth's Gravity Field Model WDM94 Complete to Degree 360[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1994, 19(4): 283-291 DOI:10.3321/j.issn:1671-8860.1994.04.001)
(  0) 0) |
| [2] |
管泽霖, 李建成, 晁定波, 等. WZD94中国重力大地水准面研究[J]. 武汉测绘科技大学学报, 1994, 19(4): 292-297 (Guan Zelin, Li Jiancheng, Chao Dingbo, et al. The Research of Gravity Geoid WZD94 in China[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1994, 19(4): 292-297)
(  0) 0) |
| [3] |
陈俊勇, 李建成, 宁津生, 等. 中国新一代高精度、高分辨率大地水准面的研究和实施[J]. 武汉大学学报:信息科学版, 2001, 26(4): 283-289 (Chen Junyong, Li Jiancheng, Ning Jinsheng, et al. A New Chinese Geoid with High Resolution and High Accuracy[J]. Geomatics and Information Science of Wuhan University, 2001, 26(4): 283-289)
(  0) 0) |
| [4] |
魏子卿, 王刚. 用地球位模型和GPS/水准数据确定我国大陆似大地水准面[J]. 测绘学报, 2003, 32(1): 1-5 (Wei Ziqing, Wang Gang. Determination of Quasi-Geoid in Mainland China Using Geopotential Model and GPS/Leveling Data[J]. Acta Geodaetica et Cartographic Sinica, 2003, 32(1): 1-5 DOI:10.3321/j.issn:1001-1595.2003.01.001)
(  0) 0) |
| [5] |
李建成. 最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651-650 (Li Jiancheng. The Recent Chinese Terrestrial Digital Height Datum Model: Gravimetric Quasi-Geoid CNGG2011[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 651-650)
(  0) 0) |
| [6] |
杨翼飞, 唐长增. 基于EGM2008地球重力场模型的广西似大地水准面优化研究[J]. 测绘通报, 2014(1): 50-53 (Yang Yifei, Tang Changzeng. The Guangxi Quasi-Geoid Optimization Research Based on EGM2008[J]. Bulletin of Surveying and Mapping, 2014(1): 50-53)
(  0) 0) |
| [7] |
佟洞, 李昱春, 宋玉兵. 江苏省陆海统一测绘基准的建设探讨[J]. 现代测绘, 2017, 40(4): 49-52 (Tong Dong, Li Yuchun, Song Yubing. Discussion on Land and Sea Unified Mapping Benchmark Construction in Jiangsu Province[J]. Modern Surveying and Mapping, 2017, 40(4): 49-52 DOI:10.3969/j.issn.1672-4097.2017.04.014)
(  0) 0) |
| [8] |
刘鹏程, 戴建清, 匡志威. 长沙市高精度似大地水准面模型的确定[J]. 城市勘测, 2014(1): 113-116 (Liu Pengcheng, Dai Jianqing, Kuang Zhiwei. The Establishment of Changsha High Accuracy Quasi-Geoid Refinement Model[J]. Urban Geotechnical Investigation & Surveying, 2014(1): 113-116 DOI:10.3969/j.issn.1672-8262.2014.01.033)
(  0) 0) |
| [9] |
杜向锋, 张兴福, 段杰. 应用卫星定位技术确定韶关市区似大地水准面[J]. 导航定位学报, 2014, 2(3): 83-86 (Du Xiangfeng, Zhang Xingfu, Duan Jie. Determination of Shaoguan City Quasi-Geoid by Using Satellite Positioning Data[J]. Journal of Navigation and Positioning, 2014, 2(3): 83-86 DOI:10.3969/j.issn.2095-4999.2014.03.018)
(  0) 0) |
| [10] |
唐秋祥, 伍百发. 湖南省似大地水准面的精度检测和特征分析[J]. 测绘科学, 2013, 38(3): 10-13 (Tang Qiuxiang, Wu Baifa. Precision Testing and Characteristics Analysis of Quasi-Geoid in Hunan Province[J]. Science of Surveying and Mapping, 2013, 38(3): 10-13)
(  0) 0) |
| [11] |
唐秋祥, 伍百发. 省级似大地水准面的局部再精化[J]. 测绘科学, 2013, 38(4): 7-9 (Tang Qiuxiang, Wu Baifa. Further Refining Provincial Local Quasi-Geoid[J]. Science of Surveying and Mapping, 2013, 38(4): 7-9)
(  0) 0) |
| [12] |
Vaníĉek P, Huang J, Novák P, et al. Determination of the Boundary Values for the Stokes-Helmert Problem[J]. Journal of Geodesy, 1999, 73(4): 180-192 DOI:10.1007/s001900050235
(  0) 0) |
| [13] |
冯进凯, 王庆宾, 黄佳喜, 等. 多个超高阶重力场模型精度分析[J]. 测绘科学技术学报, 2017, 34(4): 358-363 (Feng Jinkai, Wang Qingbin, Huang Jiaxi, et al. The Accuracy Analysis of Multiple Ultra-High-Degree Gravity Field Models[J]. Journal of Geomatics Science and Technology, 2017, 34(4): 358-363)
(  0) 0) |
2. GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2019, Vol. 39
2019, Vol. 39

