经典最小二乘估计是一种非常成熟的基于线性模型的估计方法,但现实中的模型并不都是线性的,用处理线性模型的理论去处理非线性模型,只是一种简单、近似的方法[1]。如LS(最小二乘法)、TLS(总体最小二乘)、NTLS(非线性总体最小二乘)等方法都是建立在线性化的前提下,略去高次项时不可避免地产生截断误差。究其原因,一是处理方法没有摆脱线性思维的约束;二是没有从非线性模型空间层次建立相应的平差与数据处理方法[2]。
处理非线性模型的方法大致有以下几种[3-8]:1)将非线性模型按泰勒公式展开至二次或三次项,然后再进行研究;2)保持原模型不变,根据实际模型特点选择参数初值,借助各种优化方法和迭代法搜索参数解,这种方法参数精度评价非常复杂;3)非线性模型的直接平差法,其原理是将原非线性模型按泰勒级数展开至有限次数,将其中的二次以上项(仍为非线性)作线性近似,然后将线性近似所得参数系数与原模型一次项系数合并成新的矩阵,最后进行常规最小二乘估计[1]。
本文针对多项式拟合模型的参数求解问题,借鉴第2种方法,即在不线性化的前提下,依据约束最优化方法理论,使用最速下降法进行迭代求得参数解,并与常规方法进行比较。
1 相关概念 1.1 多项式拟合模型多项式拟合模型的形式为:
| $ \quad \quad \left[ \begin{gathered} {y_1} + {e_{{y_1}}} \hfill & {y_2} + {e_{{y_2}}} \hfill & ... \hfill & {y_n} + {e_{{y_n}}} \hfill \end{gathered} \right]^{\rm{T}} = \\ \left[ \begin{gathered} 1&{x_1} + {e_{{x_1}}}& ({x_1} + {e_{{x_1}}}{)^2}&...& ({x_1} + {e_{{x_1}}}{)^m} \hfill \\ 1&{x_2} + {e_{{x_2}}}& ({x_2} + {e_{{x_2}}}{)^2}&...& ({x_2} + {e_{{x_2}}}{)^m} \hfill \\ ...&...&...&...&... \hfill \\ 1&{x_n} + {e_{{x_n}}}& ({x_n} + {e_{{x_n}}}{)^2}&...& ({x_n} + {e_{{x_n}}}{)^m} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {c_0} \hfill \\ {c_1} \hfill \\ ... \hfill \\ {c_m} \hfill \\ \end{gathered} \right] $ | (1) |
式中,yi、eyi(i=1, 2, …, n)为观测量及其误差,xi、exi(i=1, 2, …, n)为自变量及其误差,ci(i=0, 1, …, m)为待估参数。当m=1时,模型为直线拟合模型;当m=2时,模型为二次曲线回归模型;当m≥2时,模型为非线性EIV(变量误差)模型[9]。
从本质来说,该模型仍是非线性模型:
| $ {Y_x} = f\left( {x,\theta } \right) + {\varepsilon _x} $ | (2) |
式中,Yx为n×1观测量,观测量与自变量之间的非线性关系用f表示,且f为自变量x的函数,θ为待估参数。
本文通过将此类问题转化为有约束的非线性规划问题进行参数的求解。
1.2 约束最优化方法 1.2.1 有约束的非线性规划有约束的非线性规划问题的一般形式为:
| $ \left\{ \begin{array}{l} \min f\left( x \right)\\ {\rm{s}}.{\rm{t}}.\;\;\;\;s\left( x \right) \ge 0\\ h\left( x \right) = 0 \end{array} \right. $ | (3) |
其中,目标函数f:Rn→Rl(表示n维实数到1维实数的映射),不等式约束条件s:Rn→Rm,等式约束方程h:Rn→Rl。这个问题的求解是指,在容许集D={x|s(x)≥0, h(x)=0, x∈Rn}内找到一点x*,使得对于任意的x∈D都有:
| $ f({x^*}) \le f(x) $ |
而点x*就是问题(3)的最优解[10]。
1.2.2 外点法一般约束最优化问题为:
| $ \left\{ \begin{array}{l} \min f\left( x \right)\\ {\rm{s}}.{\rm{t}}.\;\;\;\;{s_i}\left( x \right) \ge 0,i = 1,2, \ldots ,m\\ {h_j}\left( x \right) = 0,j = 1,2, \ldots ,l \end{array} \right. $ | (4) |
对于式(4),可采取如下的惩罚策略:
| $ F\left( {x,\mu } \right) = f\left( x \right) + \mu \alpha \left( x \right) $ | (5) |
其中,罚函数为:
| $ \begin{array}{c} \alpha \left( x \right) = \sum\limits_{j = 1}^l {{{[{h_j}\left( x \right)]}^2}} + \sum\limits_{i = 1}^m {{{[{s_i}\left( x \right)]}^2}} u({s_i}\left( x \right)),\\ u({s_i}\left( x \right)) = \left\{ \begin{array}{l} 0,{s_i}\left( x \right) \ge 0\\ 1,{s_i}\left( x \right) < 0 \end{array} \right.,i = 1,2, \ldots ,m \end{array} $ |
把F(x, μ)称为约束问题(4)的增广目标函数,μ(>0)称为罚因子,μα(x)称为惩罚项。
对于某个给定的μ,若xμ是无约束问题(5)的极小点,则xμ也是约束问题(4)的极小点的充要条件是xμ恰是问题(4)的容许点。
把μ取为一个趋于正无穷大的正数序列{μk},并对k=0, 1, 2, …依次求解无约束问题:
| $ F(x,{\mu _k}) = f\left( x \right) + {\mu _k}\alpha \left( x \right) $ | (6) |
达到求解约束问题(4)的方法称为外点法[10]。
1.2.3 改进的外点法对于多项式拟合模型(1),有n组观测值(x1, y1),(x2, y2),…,(xm, ym),…,(xn, yn),将第m组观测值(xm, ym)代入式(2)并移项得目标函数:
| $ {\varepsilon _{{x_m}}} = {Y_{{x_m}}} - f({x_m},\theta ) $ | (7) |
为方便计算,取其平方作为目标函数:
| $ \varepsilon _{{x_m}}^2 = {[{Y_{{x_m}}} - f({x_m},\theta )]^2} $ |
将前(m-1)组观测值代入式(2)且认为εxi=0(i=1, 2, …, m-1),移项得等式约束条件:Yx1-f(x1, θ)=0,Yx2-f(x2, θ)=0,…,Yxm-1-f(xm-1, θ)=0。
在上述约束条件方程中,分别选取1, 2, …, m-1个构造罚函数:
| $ {\alpha _p}\left( \theta \right) = \sum {[{Y_{{x_p}}} - f({x_p},\theta )]^2} $ | (8) |
式中,p为选取的已知量。
改进的外点法步骤如下:
1) 选定初始迭代点θ0及罚因子μ(>0),选择观测值构造罚函数;
2) 用最速下降法[10]求解无约束问题:
| $ \min {\varepsilon _{{x_m}}} + \mu \alpha \left( \theta \right) $ | (9) |
得极小点θ1;
3) 计算范数差值
4) 改变罚函数(共2m-1-1种选择方式),当
|
|
表 1 观测数据 Tab. 1 The simulated data |
用MATLAB编写最速下降法程序,步长搜索采取不精确一维搜索,区间搜索采用黄金分割法,最大迭代次数为8 000,终止条件为ε=10-6。以第1组数据建立等式约束条件,第7组数据构造目标函数,迭代初值为PEIV法所求参数。在不同的罚因子下,求得参数与真值范数差值列于表 2。
|
|
表 2 罚因子大小的影响 Tab. 2 The size of the penalty factor |
可以看到,当罚因子较大时,迭代次数比较少,收敛速度较快;当罚因子较小时,迭代次数较多,收敛速度较慢。μ越大,增广目标函数F(x, μ)的Hesse矩阵的条件数越坏。因此,在迭代开始时,将μ值取小一些[10]。
2.2 目标函数的位置对计算结果的影响以第1、1/3、1/2/3组观测值建立等式约束条件,分别以第7~17组观测值构造目标函数,所得范数差值如表 3(单位mm)和图 1所示。
|
|
表 3 目标函数选点位置的影响 Tab. 3 The influence of the objective function for choosing location |
从图 1看出,随着用于构造目标函数的观测值位置的后移,范数差值呈现降低(或不变)的趋势,说明目标函数选在第7点及以后是合理的。

|
图 1 目标函数选点位置的影响 Fig. 1 The influence of the objective function for choosing location |
选择1/3点建立等式约束条件,第7点构造目标函数,罚因子μ=1 000,用MATLAB的randic模拟100组[-10, -10, -10]到[10, 10, 10]的随机整数,同时加上以normrnd模拟的均值为0、方差为0.5的随机数作为迭代初值,并计算其迭代结果与参数真值的差值范数,将计算结果以范数差值升序排列绘制成图 2。可以看到,随着范数差值的增加,迭代初值与其并无明显关联。根据表 4,当以与参数真值较为接近的数值作为迭代初值时,迭代结果与之前相比都有一定改善,说明迭代结果受到迭代初值的影响,但又不完全依赖于迭代初值,从而说明以PEIV的计算结果(文献[9]中最精确的值)作为迭代初值是合理的。
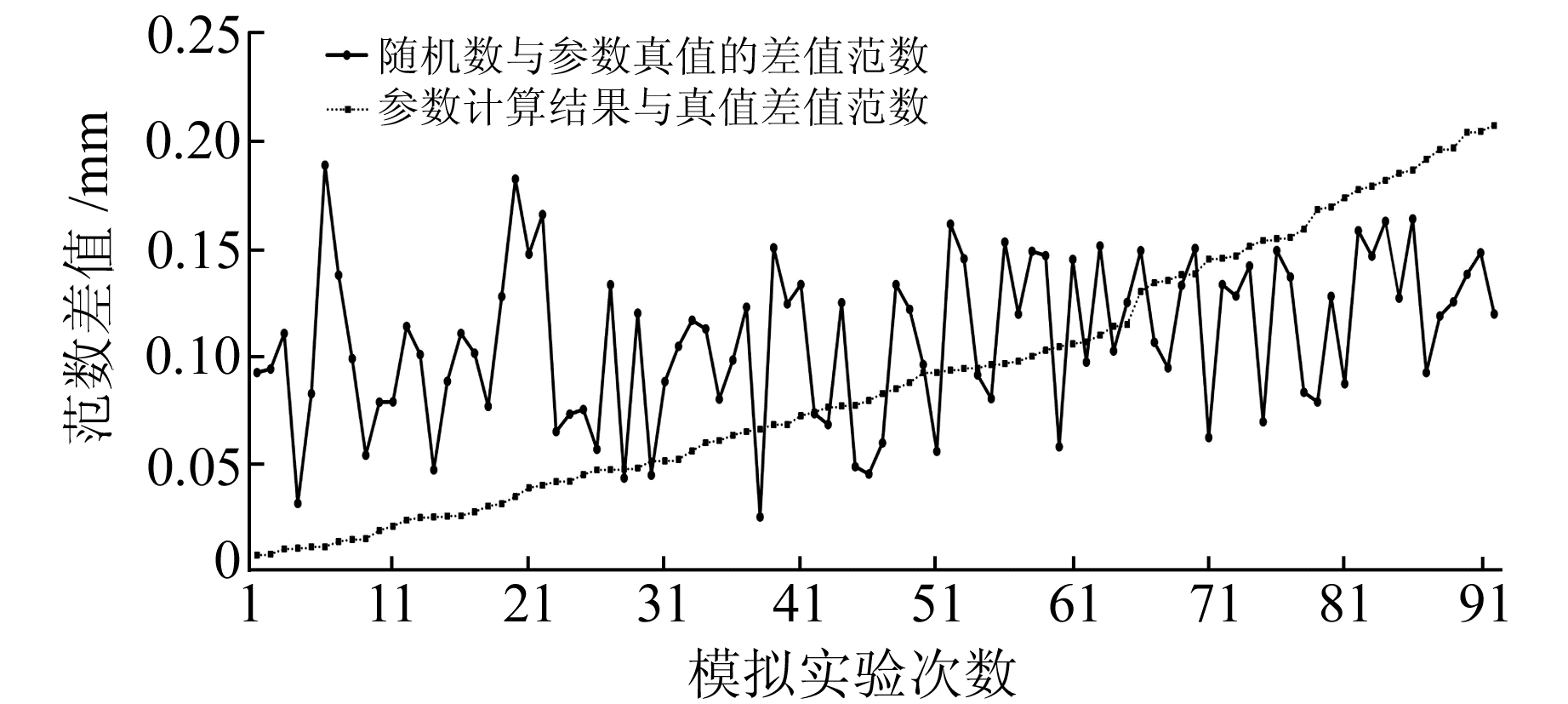
|
图 2 范数差值与迭代初值的关系 Fig. 2 Norm difference and the relationship of the initial value of iteration |
|
|
表 4 以参考文献计算结果作为迭代初值求得的范数差值 Tab. 4 Reference calculation results as the iterative initial value for the norm of the difference |
以上3点的讨论表明,使用改进的外点法求解多项式函数模型参数具有一定可行性。
3 算例及其分析令m=7,即用第7组观测值建立目标函数,前6组观测值建立等式约束条件方程,初始迭代点为PEIV法求得的参数值,罚因子定为μ=1 000,使用上文改进的外点法进行求解,结果见表 5、6。
|
|
表 5 改进外点法的计算结果 Tab. 5 Calculation results of improved outside point method |
|
|
表 6 不同方法的解算结果[9] Tab. 6 The results from different methods |
从表 5、6可以看出:1)基于本文方法求得的参数精度普遍较高,与LS、TLS、NTLS等方法相比具有一定优势,而精度最高时的范数差值0.046 3更是远超PEIV法结果;2)算例所用最速下降法设定迭代次数为8 000次,将迭代结果分成2种情况(8 000次之内是否完成所有迭代),在各自的情况下,范数差值的量级有所不同,在完成迭代的情况参数精度要强于止于8 000次时;3)范数差值与目标函数拟合绝对误差具有一定的相关性,而在实际中往往无法事先得知参数真值,依此方法可挑选出精度最高的参数;4)能够计算出参数值的选点方式均仅含前4个观测值建立等式约束条件,换言之,含后2点的等式约束使迭代发散,而选点为距离目标函数点且数量较小时,达到最佳效果。
4 结语本文依据最优化方法理论,将多项式模型拟合的参数求解转化为有约束的非线性规划问题,突破以往线性思维的约束,从而避免舍去高次项时产生的截断误差。通过对罚因子、目标函数和迭代初值的分析,说明对外部罚函数法改进的合理性。通过算例,证明该算法的可行性,并且与现有几种方法比较,显示出该方法在求解精度上的优势;且提供选点方法,使其在实际应用中具有一定的指导作用。
| [1] |
张俊, 独知行, 杜宁, 等. 非线性模型的补偿最小二乘估计[J]. 大地测量与地球动力学, 2005, 35(1): 122-125 (Zhang Jun, Du Zhixing, Du Ning, et al. Penalized Least Square Estimator for Non-Linear Models[J]. Journal of Geodesy and Geodynamics, 2005, 35(1): 122-125)
(  0) 0) |
| [2] |
李朝奎. 非线性模型空间测量数据处理理论及其应用[M]. 北京: 化学工业出版社, 2013 (Li Chaokui. Theory and Application of Data Processing in Space of Nonlinear Models[M]. Beijing: Chemical Industry Press, 2013)
(  0) 0) |
| [3] |
Box M J. The Occurrence of Replications in Optimal Designs of Experiments to Estimate Parameters in Nonlinear Models[J]. Journal of the Royal Statistical Society(Ser B), 1968, 30(2): 290-302
(  0) 0) |
| [4] |
Bates D M, Watts D G. Relative Curvature Measures of Non-Linearity[J]. Journal of the Royal Statistical Society(Ser B), 1980, 42(1): 1-25
(  0) 0) |
| [5] |
王新洲. 非线性模型参数估计的直接解法[J]. 武汉测绘科技大学学报, 1999, 24(1): 64-67 (Wang Xinzhou. A Direct Solution Method of Parameter Estimation of Nonlinear Model[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(1): 64-67)
(  0) 0) |
| [6] |
陶本藻. 关于测量中非线性模型的估计问题[J]. 测绘通报, 1998(2): 6-8 (Tao Benzao. On the Estimation of Nonlinear Models in Measurement[J]. Bulletin of Surveying and Mapping, 1998(2): 6-8)
(  0) 0) |
| [7] |
韦博成. 近代非线性回归分析[M]. 南京: 东南大学出版社, 1989 (Wei Bocheng. Modern Nonlinear Regression Analysis[M]. Nanjing: Southeast University Press, 1989)
(  0) 0) |
| [8] |
李朝奎, 黄健柏, 黄力民. 基于非线性误差模型的参数估计[J]. 测绘工程, 2000, 9(3): 19-22 (Li Chaokui, Huang Jianbai, Huang Limin. Parameters Estimation Based on Nonlinear Error Models[J]. Engineering of Surveying and Mapping, 2000, 9(3): 19-22 DOI:10.3969/j.issn.1006-7949.2000.03.005)
(  0) 0) |
| [9] |
王乐洋, 温贵森. 一种基于Partial EIV模型的多项式拟合解法[J]. 大地测量与地球动力学, 2017, 37(7): 737-742 (Wang Leyang, Wen Guisen. A Kind of Polynomial Fitting Method Based on Partial EIV Model[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 737-742)
(  0) 0) |
| [10] |
张薇, 薛嘉庆. 最优化方法[M]. 沈阳: 东北大学出版社, 2004 (Zhang Wei, Xue Jiaqing. Optimization Method[M]. Shenyang: Northeast University Press, 2004)
(  0) 0) |
| [11] |
胡川, 陈义. 非线性整体最小平差迭代算法[J]. 测绘学报, 2014, 43(7): 668-674 (Hu Chuan, Chen Yi. An Iterative Algorithm for Nonlinear Total Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 668-674)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

